干濕循環下受彎鋼筋混凝土梁的氯鹽侵蝕

蔡健，李名鎧，陳慶軍，賴駿，魏沐楊

(1.華南理工大學土木與交通學院，廣東廣州，510641；2.亞熱帶建筑科學國家重點實驗室，廣東廣州，510641)

臨海混凝土結構根據所處的環境可分為不同的結構分區。其中，干濕交替區域的混凝土在對流和擴散的共同作用下，氯離子以較快速度滲透至混凝土內部，因此，該區域是結構耐久性設計的關鍵部位。混凝土結構在服役過程中的受荷狀態會對氯離子的輸運產生影響，而彎曲荷載則是結構構件服役過程中最常見的荷載類型之一。因此，對干濕環境下受彎混凝土構件的氯鹽侵蝕機理進行研究，提出易用的計算方法，對其耐久性設計及壽命預測具有重要意義。對于干濕交替區域的氯鹽侵蝕，采用傳統的菲克第二定律擬合檢測數據存在一定的誤差。因此，國內外學者對非飽和狀態下混凝土中氯鹽侵蝕機理展開了廣泛研究。ABABNEH 等[1?2]建立了非飽和狀態下混凝土中氯離子傳輸模型。改進后的模型較為復雜，一般無法直接求解，部分學者嘗試采用差分方法進行解答，并通過試驗進行驗證[2?4]。此外，在荷載作用下，混凝土中出現微觀和宏觀裂縫，改變氯離子的侵蝕速度。YE 等[5]對鋼筋混凝土梁施加彎曲荷載并進行干濕循環試驗，發現低壓應力對氯離子侵蝕有阻礙作用，高壓應力和拉應力有促進氯離子侵蝕的作用；并以混凝土應力和峰值應力的比值為變量提出了冪函數形式氯離子擴散系數的荷載影響公式。WANG 等[6?7]基于試驗提出以荷載比為變量的氯離子擴散系數修正系數。陸春華等[8]針對受彎開裂混凝土，提出考慮裂縫效應的“等效氯離子擴散系數”來進行簡化分析。蔡健等[9?10]在飽和狀態下鋼筋混凝土、非飽和狀態下的預應力混凝土梁的侵蝕中引入損傷因子，以考慮荷載的影響。總體而言，目前針對彎曲荷載下的氯鹽侵蝕的研究主要以試驗數據建立影響函數修正氯離子擴散系數，從而對荷載效應進行考慮，但相關的數值模擬研究成果較少，缺乏詳細闡述。為此，本文以荷載、侵蝕時間為變量開展彎曲荷載與干濕循環共同作用下混凝土的氯鹽侵蝕試驗；介紹一種考慮荷載及干濕循環的數值模擬方法，并擬合荷載影響系數，對構件層次的氯離子擴散場和荷載場進行耦合分析。

1 模型的建立

1.1 非飽和狀態下混凝土中氯離子的輸運

氯離子在干濕交替區混凝土中的傳輸是典型的非飽和輸運過程：氯離子除了隨混凝土孔隙液離子質量分數梯度發生擴散外，還將隨著孔隙液飽和度梯度發生對流作用。由于氯離子的輸運發生于混凝土的孔隙溶液中，孔隙溶液飽和度必然會對氯離子的擴散速度造成影響。李春秋等[2,11]提出了指數型、多項式型函數對氯離子擴散系數和孔隙飽和度之間的關系進行描述。本文參考文獻[2,4]，取非飽和狀態下混凝土內水分及氯離子傳輸模型的一維形式為：

式中：C為氯離子質量分數；s為孔隙液濃飽和度；Ds為水分擴散系數；DCl為氯離子擴散系數；r為飽和度影響系數，考慮到s與DCl呈線性關系，r=1；t為實際暴露時間。

對于氯離子擴散系數DCl，由于混凝土水化等作用的持續進行，混凝土的孔隙結構逐漸密實，會呈指數衰減，t時刻的擴散系數D(t)可按下式計算：

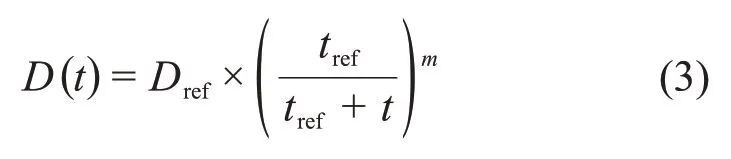
式中：Dref為時間tref對應的參照氯離子擴散系數；m為齡期衰減系數，與膠凝材料的環境及種類有關[4,12]。

對于水分擴散系數Ds，金偉良[4,13?14]等提出了不同的模型。本文采用劉鵬等[15]提出的簡化的水分擴散模型，其形式如下。

濕潤過程：

干燥過程：

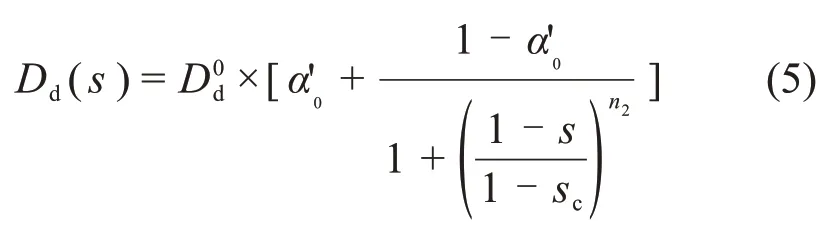
式中：和分別為濕潤和干燥過程飽和狀態水分擴散系數；α'0為相對濕度極低時Ds與的比值；sc為時的相對濕度；n1和n2分別為濕潤和干燥過程中Dd變化速率的系數；e 為自然底數。

1.2 考慮荷載作用下的混凝土中氯離子的輸運

荷載作用會對混凝土中的氯鹽侵蝕速度產生影響，目前國內外學者通常基于試驗數據對氯離子擴散系數進行修正，但采用的自變量也各有不同。WANG 等[7?8]分別以彎曲荷載和裂縫寬度為變量建立函數對氯離子擴散系數進行修正；吳靜新[16]以體積應變和孔隙率作為耦合變量，建立了荷載與氯鹽侵蝕共同作用下的氯離子傳輸模型。ALKUTTI[17]提出以標量損傷作為自變量考慮荷載的影響，可以體現應力對氯離子擴散速度的影響，且可推廣到不同的混凝土材料。因此，本文采用ALKUTTI 提出的考慮結構損傷的氯離子擴散系數D，其表達式如下：

式中：De為不考慮結構損傷時的氯離子擴散系數，F(d)為以標量損傷d為自變量的混凝土損傷影響函數，劉鵬等[15]基于試驗數據采用多項式形式對其進行了擬合。

AL-KUTTI[17]以混凝土彈性剛度的退化來描述混凝土損傷，得出標量損傷與混凝土應變之間的關系：

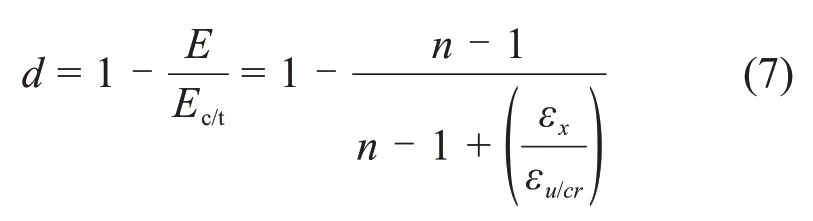
式中：εx為混凝土軸向應變，當εx＜0 即混凝土受壓時，Ec/t取Ec，εu/cr取εu，當εx＞0 即混凝土受拉時，Ec/t取Et，εu/cr取εcr；Ec和Et分別為混凝土未受損傷時的受壓割線模量和受拉割線模量；εu和εcr分別為混凝土的極限壓應變和開裂應變；n為混凝土損傷時的材料參數，在受拉與受壓時取值不同。

2 數值模型的建立

2.1 COMSOL物理場模塊設置

本文使用COMSOL Multiphysics 5.2a實現多物理場的耦合分析，采用“固體力學”物理場實現混凝土受荷的模擬，采用“桁架”物理場實現鋼筋受荷的模擬，采用“系數型偏微分方程”物理場實現干濕循環下氯離子輸運的模擬。“系數型偏微分方程”模塊的控制方程如下：

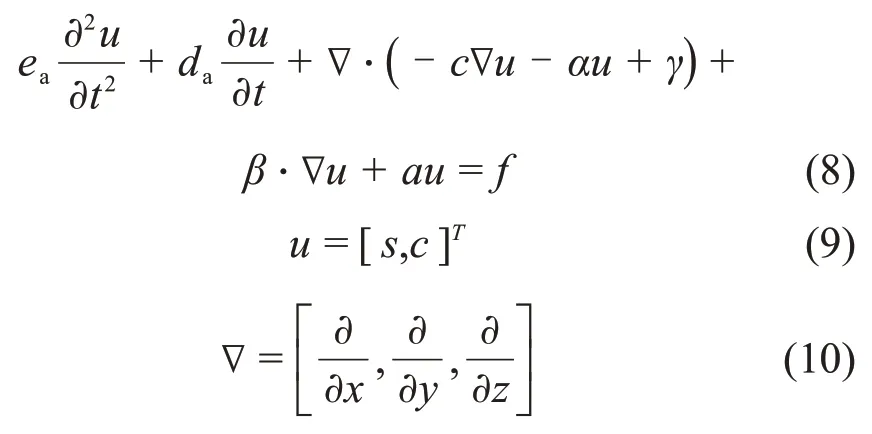
式中：c為擴散系數；a為吸收系數；f為源項；ea為質量系數；da為阻尼或質量系數；α為守恒通量對流系數；β為對流系數；γ為守恒通量源。本文中a，f，ea，β和γ均設置為0，da取1。

2.2 模型試算

為了檢驗模型的合理性，以干濕循環下3點受彎鋼筋混凝土梁為對象進行模型試算分析。試算模型的條件參見文獻[8]。其干濕循環制度以14 d為1個周期，干燥和濕潤過程的時間相同。模型參數參照文獻[2]。

取最后1個周期的濕潤與干燥過程的計算結果進行分析。記濕潤過程的起始時間為t1，結束時間為t2；干燥過程的起始時間為t3，結束時間為t4。以距中100 mm處為例，各個時間的飽和度和氯離子質量分數如圖1所示。

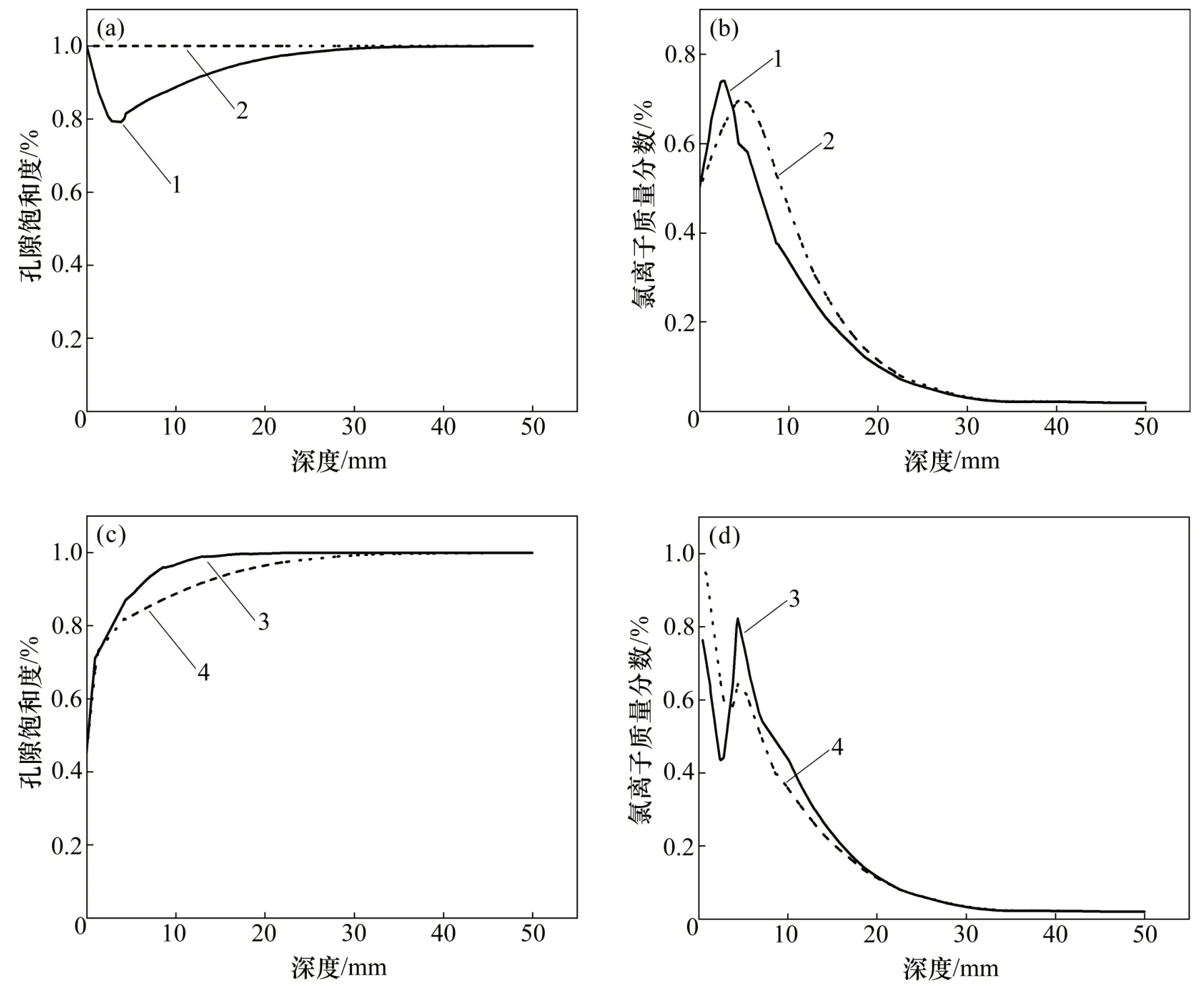
圖1 模型試算結果Fig.1 Trial results of model

由圖1(a)可見：在t1時刻前試件處于干燥過程，孔隙液隨表面蒸發向外界遷移，滯后效應使孔隙飽和度曲線呈現顯著的鋒面。在t1時刻試件從干燥過程轉變為濕潤過程，孔隙滲流使得淺層處混凝土的飽和度有所提高，飽和度達到極小值。隨著濕潤過程不斷進行，混凝土內孔隙飽和度逐漸恢復至t2時刻的1.0。由圖1(b)可見：與此同時，外界氯離子隨溶液滲入混凝土中，在混凝土的淺層區域發生對流和擴散的綜合作用。由于對流效應對氯離子輸運的貢獻明顯高于擴散效應，淺層中氯離子的補給速度高于其向內部擴散的速度，往往會形成淺層區形成1個峰值。

由圖1(c)可見：在t3時刻，試件由濕潤過程轉入干燥過程，出現如前所述的飽和度下降鋒面。隨著干燥過程不斷進行，內部孔隙液逐漸向外遷移，影響逐漸深入；鋒面往混凝土內部推進，陡峭程度下降。由圖1(d)可見：與此同時，氯離子隨孔隙溶液向混凝土表層遷移，使得濕潤過程中形成的峰值變得陡峭，接近表面處的氯離子質量分數也有所提高，如t3時刻曲線所示。隨著干燥過程持續，氯離子隨孔隙液逐漸向表面輸運，峰值逐漸變小，表層處氯離子質量分數上升。

對于三點彎曲梁，從跨中到支座處，混凝土應變逐漸增大，損傷程度不斷提高，氯離子擴散速率將會有所提高。不同深度處的氯離子試算結果如圖2所示。由圖2可見：對于同一深度的氯離子質量分數，由跨中到支座處呈現逐漸減小的趨勢，可見該數值模型可以有效考慮荷載造成的混凝土損傷對氯鹽侵蝕的影響，可進一步用于后續分析。

3 試驗驗證

3.1 試驗材料

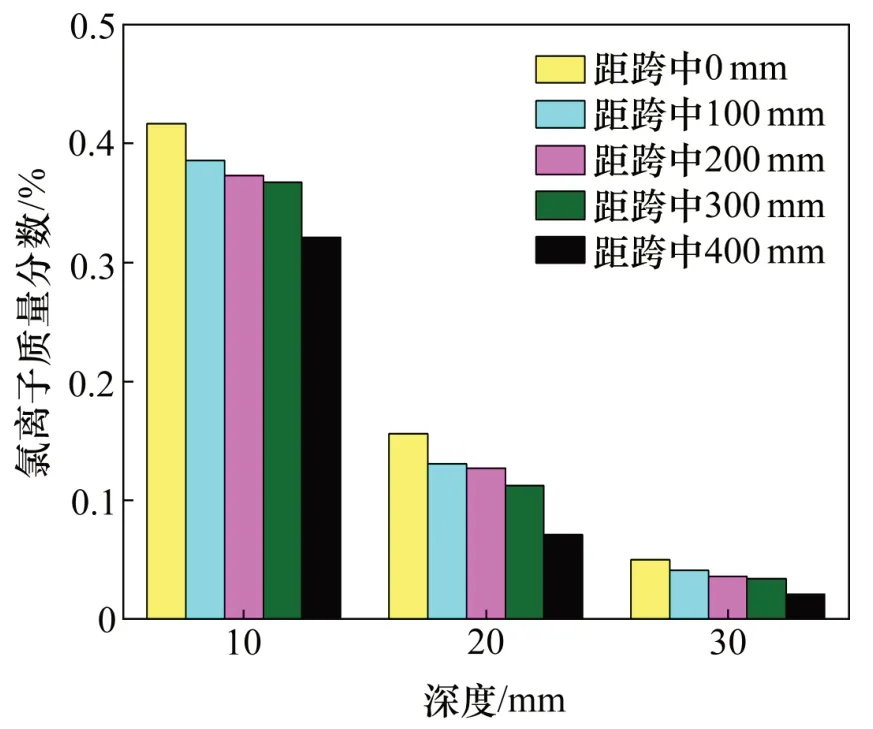
圖2 不同深度處的氯離子質量分數試算結果Fig.2 Trial results of chloride ion mass fraction profile at different depths

本試驗采用強度等級為C40的普通硅酸鹽水泥、粒徑為5～25 mm的碎石以及天然江砂。混凝土不摻加任何外加劑，采用普通自來水作為拌合水和養護水。試驗采用的水灰比為0.4，混凝土中各材料用量為：水泥455 kg/m3，水182 kg/m3，砂755 kg/m3，石子1 465 kg/m3。其混凝土標準立方體試塊28 d抗壓強度平均值為49.8 MPa。

對本試驗中采用的鋼筋進行拉伸試驗，測得直徑8 mm 鋼筋的屈服強度和極限強度分別為308.2 MPa和484.9 MPa，直徑14 mm 鋼筋的屈服強度和極限強度分別為471.7 MPa和628.1 MPa。

3.2 試件設計與制作

設計制作了7 根鋼筋混凝土梁試件，試件長×寬×高為1 000 mm×150 mm×180 mm，保護層厚度取35 mm，各試件具體參數見表1，試件配筋及加載方式如圖3所示。表1中：S0僅用于確定混凝土梁的極限承載力，不進行氯鹽侵蝕；S1，S2和S3進行182 d干濕循環；S4，S5和S6進行364 d干濕循環。文獻[18]將鋼筋混凝土構件正截面的受力裂縫控制等級分為3級，本文試驗通過設置荷載比P/Pcr(即施加的彎曲荷載與極限彎曲承載力的比值)為0，23.7%和37.6%的試件分別對應一級、二級和三級裂縫控制等級。

表1 試件具體參數Table 1 The specific parameters of test specimens

對進行干濕循環的試件(S1～S6)只保留其受拉下底面(150 mm × 1 000 mm)作為氯離子滲透面，將其他5個截面的表面浮漿磨去，用酒精清洗干凈后，用環氧樹脂涂刷封閉，保證氯離子只從底面進行滲透。

3.3 試驗方法

待標準固化期結束后，首先對試件S0 進行兩點靜力加載試驗，確定S0 極限承載力為255 kN。采用如圖4所示的加載裝置將S1～S6兩兩自錨，施加對應的彎曲荷載，通過螺桿上的力傳感器監測施加在螺栓上的預緊力。

荷載施加完成后，將試件放置于質量分數為5%的NaCl溶液中進行干濕循環試驗。每個干濕循環周期為14 d，干濕周期比例取1:1，以模擬海工環境下混凝土的干濕交替區域。由于試驗周期較短，本文暫不考慮錨桿的應力松弛以及混凝土裂縫的自愈合行為。

圖3 鋼筋混凝土梁尺寸和配筋圖Fig.3 Dimension and reinforcements of specimens

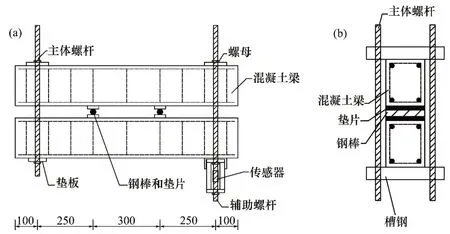
圖4 彎曲荷載加載裝置圖Fig.4 Flexural loading devices

待干濕循環試驗結束后，將試驗梁取出，置于干燥處晾干7 d，隨后用沖擊鉆在各開裂試件純彎段、彎剪段沿侵蝕面豎直方向鉆孔取粉，試件芯樣取樣位置如圖5所示。最大深度取至50 mm處，同一位置沿深度方向，前20 mm每隔5 mm取1次粉樣，30～50 mm每隔10 mm取1次粉樣；參考文獻[19]，將粉末試樣分別過0.63 mm 篩，并裝入鋁盒中，置于(105±5)℃的烘干箱中烘干2 h，取出放入干燥器冷卻至室溫，測定混凝土中水溶性氯離子(自由氯離子)質量分數。

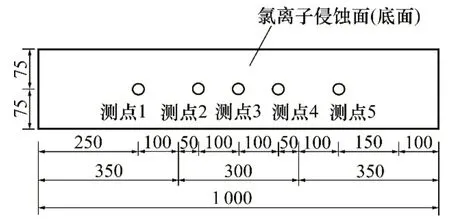
圖5 試件取樣位置Fig.5 Sampling position of specimen

3.4 試驗結果分析

對純彎段、彎剪段測點在各深度的氯離子質量分數分別計算平均值，得到不同荷載、侵蝕時間的6條試驗梁不同受力部位的氯離子質量分數隨深度變化曲線，如圖6所示。

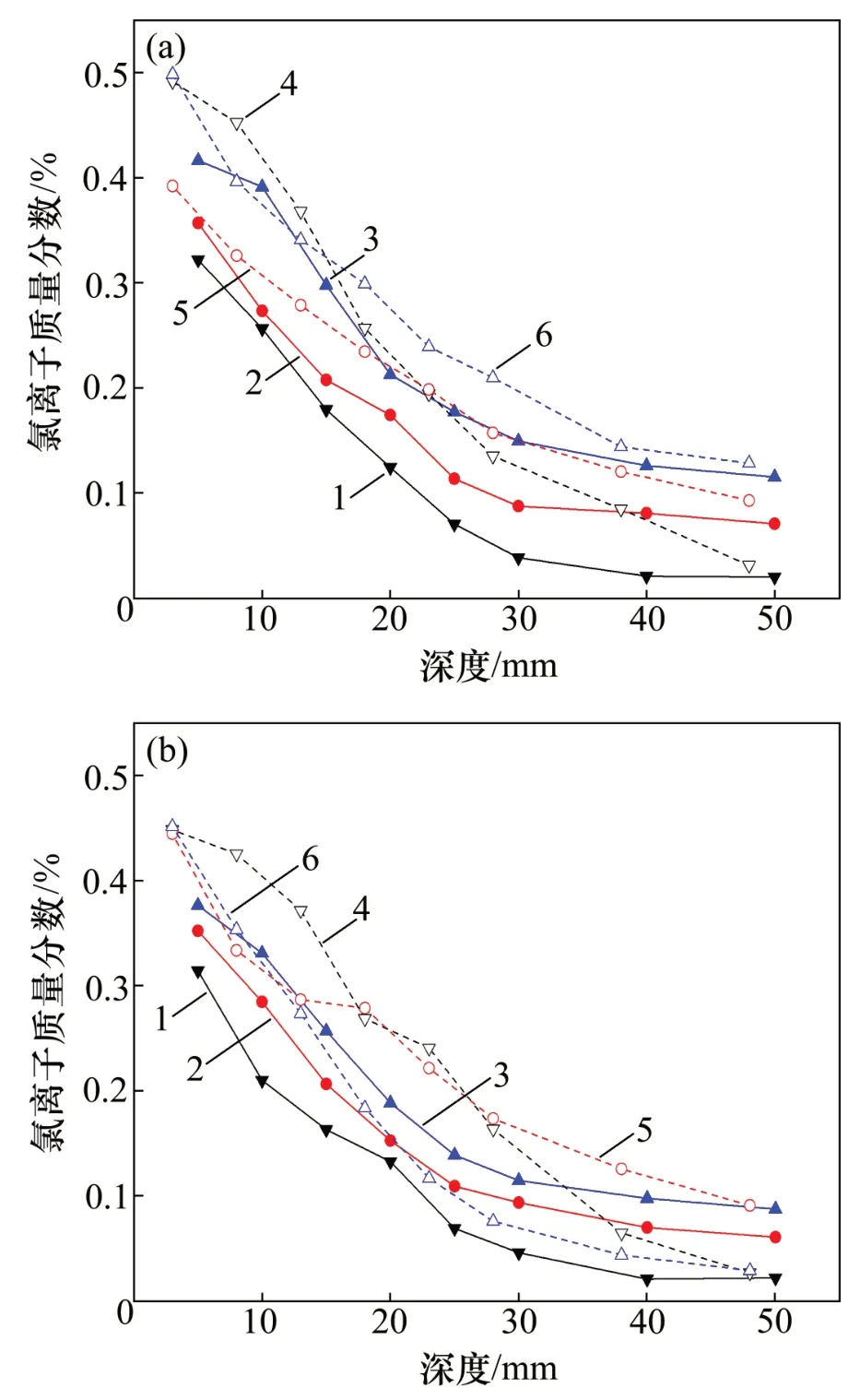
圖6 試件氯離子質量分數與深度的關系Fig.6 Relationship between chloride ion mass fraction of specimens and depth

除S6 彎剪段外，隨彎曲荷載從無荷載增加至37.6%，對于相同侵蝕時間的試驗梁(圖6中實心圖標和空心圖標分別為182 d和364 d 侵蝕時間下的結果)，相同深度處的氯離子質量分數整體上增大。其主要原因是隨著荷載的提高，試驗梁受拉區混凝土的損傷程度提高，逐漸產生微觀裂縫，導致其孔隙連通度增大；而隨著宏觀裂縫的出現和擴展，氯離子逐漸開始從裂縫內表面進行滲透。

除S6彎剪段外，隨著侵蝕時間從182 d增加至364 d，對于相同彎曲荷載下的試驗梁(即圖6 中同種形狀圖標)，相同深度處的氯離子質量分數整體上增大。其原因是隨著侵蝕時間延長，氯離子從侵蝕面不斷向內輸運，質量分數不斷提高。

在S6 試件彎剪段，測點5 所在位置混凝土截面完好，與荷載裂縫之間存在較遠的距離，氯離子擴散速度較慢。因此，S6 彎剪段測得的氯離子質量分數較低是合理的。

通過圖6對比可得：整體而言，相同深度處純彎段的氯離子質量分數高于彎剪段。這是因為對于試驗梁，純彎段受到的彎矩較大，受拉區拉應力較高，損傷程度較大，氯離子的輸運速度明顯加快。

4 數值分析

4.1 模型參數的確定

在“全局定義”版塊輸入模型計算所需參數及函數，對試驗梁模擬時采用的參數如表2所示。

在混凝土表層對流區深度內部，氯離子的滲透主要以擴散為主，可以采用Fick 第二擴散定律反映不同位置、時間的氯離子質量分數[8,20]：

式中：C(x,t)為暴露時間t深度為x處的氯離子質量分數；C0為混凝土中的初始氯離子質量分數；Cs為混凝土表面氯離子質量分數；x為據混凝土表面的深度；Da為表觀擴散系數；Δx為表面對流區深度；erf(x)為高斯誤差函數。

由于S1和S4 試驗數據沒有出現明顯的對流區，本文認為其對流區深度小于5 mm，在擬合時采用5 mm以后的試驗數據。此外，假定混凝土中的初始氯離子質量分數為0，故C0=0。借助MATLAB數據擬合工具箱，應用式(11)對無荷載的S1和S4 各測點數據進行擬合分析，結果如圖7所示，得到182 d和364 d 氯離子表觀擴散系數分別為1.014 0 mm2/d和0.904 4 mm2/d。結合式(3)，設tref為28 d，計算得28 d參考氯離子擴散系數Dref,28=1.73×10－11m2/s，齡期衰減系數m=0.19。

表2 模型參數Table 2 Parameters of model

根據HALL[21]和LEECH[22]建議，濕潤過程水分擴散系數的參數n1取6。干燥過程水分擴散系數相關參數參考文獻[21?24]取值。

AL-KUTTI根據試驗數據擬合的荷載修正函數在應變較大時與其他文獻結果有較大偏差[15]，因此，在文獻[25]的試驗數據上，擬合了以標量損傷為變量的荷載影響函數：

其形式如圖8所示。由于現有研究中反映混凝土應變與氯離子擴散規律的試驗數據不足，其適用性有待更多試驗進行驗證。此外，由于壓應變對氯離子擴散系數的影響尚未有定論[5?6,15]，且本文的研究對象為受拉區，故模擬中僅考慮受拉損傷。

圖7 表觀氯離子擴散系數擬合Fig.7 Apparent chloride diffusion coefficient fitting

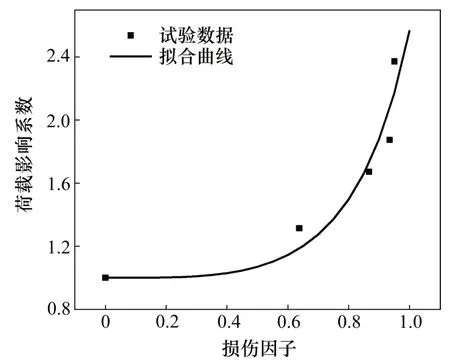
圖8 荷載影響系數與混凝土標量損傷關系圖Fig.8 Relationship between concrete scalar damage and loading influence coefficient

4.2 模型的建立

材料的參數取值按照材性試驗結果輸入；采用內置的Ottosen模型作為混凝土的破壞準則。

建立“固體力學”物理場(混凝土)，設置支座條件為一端鉸接、一端滑動，在加載面添加均勻分布荷載；建立“桁架”物理場(鋼筋)，通過“指定位移”使鋼筋和混凝土變形協調；建立“系數型偏微分方程”(氯離子)，根據式(1)～(2)對該控制方程的參數設置守恒通量對流系數α和擴散系數c。α對于水分傳輸方程取為0，對于氯離子傳輸方程α=Ds×ds/dz；根據式(3)和(6)考慮荷載和齡期對氯離子擴散系數c的影響，其參數確定過程見4.1節。

因試驗采用單面侵蝕，為模擬氯離子的一維滲透，在氯離子侵蝕面設置“狄氏邊界條件”，指定邊界質量分數為0.5%；其他5個面邊界條件設置為“零通量”。

由于試驗所關注的對象為試驗梁受拉區50 mm深度內的氯離子質量分數，通過“加密層”對受拉區邊緣的網格進行精密劃分。

干濕循環和荷載耦合分析通過COMSOL 研究步實現：步驟1為穩態計算，選擇固體力學物理場接口，計算混凝土梁在荷載作用下的力學響應；步驟2和3為瞬態計算，分別計算濕潤和干燥過程荷載作用下混凝土梁中氯離子的輸運進程；后續步驟皆為干濕循環過程。每1個步驟調用上1個步驟的解進行運算。

4.3 計算結果

以S2，S4和S6為例，提取試件純彎段、彎剪段的測點有限元結果與試驗數據進行對比，結果如圖9所示。由圖9可見：數值模擬與試驗研究的結果整體上吻合良好；對于施加彎曲荷載的試驗梁，由于宏觀裂縫的出現，各測點氯離子質量分數的數據離散性較大，但COMSOL 擬合結果更為貼近上限值，較為保守；對于S6 彎剪段，如圖9(f)所示，測點5的數據明顯偏離數值模擬結果，這與3.4中的試驗結果分析相吻合。因此，本文通過混凝土力學損傷來考慮荷載對氯離子在混凝土內輸運影響的方法合理可行，所采用的力學損傷函數較好地模擬本文的試驗結果。

圖10所示為COMSOL計算所得的混凝土梁軸向應變云圖(以182 d 試驗梁為例)。試驗梁的軸向應變與所受的彎曲荷載相對應。S2 跨中區域最大拉應變達到3.09×10-4與混凝土的受拉開裂應變較為接近。S3 跨中區域最大拉應變達到7.94×10-4，遠大于混凝土的受拉開裂應變。可以推斷，此時混凝土達到開裂狀態，出現多條宏觀裂縫。試件的應變情況與試驗方案設定的3個裂縫控制等級要求基本符合。

圖9 氯離子質量分數數值模擬結果與試驗結果對比Fig.9 Comparison of numerical simulation and experiments on chloride ion mass fraction

圖11所示為182 d的3 條試驗梁的混凝土損傷情況。由圖11 可知：隨著荷載的提高，混凝土的標量損傷沿著深度方向和跨中方向增長，損傷區域與損傷程度擴大，與試驗梁的荷載、應變狀態相一致。

圖10 軸向應變圖Fig.10 Diagrams of strain along axial direction

圖11 182 d試件標量損傷d云圖Fig.11 Scalar damage parameter d diagram of 182 d specimens

圖12 沿侵蝕面不同深度處的氯離子質量分數Fig.12 Chloride ion mass fractions at different depths from erosion surface

圖12所示為沿侵蝕面不同深度處的氯離子質量分數分布(以梁S3 為例)。由圖12 可知：對于同一試驗梁同一深度處，氯離子質量分數在純彎段基本保持在一個水平，在彎剪段往遠離跨中方向逐漸降低，這是由于在純彎段彎矩保持定值，梁受拉區的軸向應力在純彎段基本保持一致，損傷程度接近，氯離子侵蝕速度接近；而彎矩在彎剪段往兩端逐漸遞減，軸向應力逐漸降低，損傷程度也隨之降低，氯離子侵蝕速度逐漸降低。

5 結論

1)隨著彎曲荷載和侵蝕時間的提高，混凝土梁內的氯離子質量分數不斷提高。對于四點加載的混凝土梁的受拉區，純彎段的氯離子質量分數明顯高于彎剪段氯離子質量分數。

2)考慮混凝土力學損傷可以針對不同損傷部位設置不同的氯離子擴散系數，從而考慮荷載作用對氯離子在混凝土內傳輸特性的影響。

3)采用COMSOL 模擬干濕循環下承受彎曲荷載的混凝土梁的氯鹽侵蝕，所提出的荷載影響函數可以較好地擬合本文的試驗結果。