隧道近距下穿管線的爆破振動特征及安全標準

管曉明，張良，王利民，傅洪賢，余道明，陳剛，丁一，姜萬里

(1.青島理工大學土木工程學院，山東青島，266033；2.河北建設勘察研究院有限公司，河北石家莊，050031；3.河北省巖土工程研究中心，河北石家莊，050031；4.青島理工大學理學院，山東青島，266033；5.北京交通大學土木建筑工程學院，北京，100040；6.北京市市政三建設工程有限責任公司，北京，100022)

地下管線作為城市的大動脈和生命線工程，承擔著送水、送油、送燃氣、通訊及供電等重要使命。隧道爆破沖擊振動無疑會對地下管線的安全運行構成嚴重威脅。隧道近距穿越地下管線的爆破振動響應特征、損傷機理及安全防控是隧道建設面臨的重大理論與技術難題，由于對管線的爆破振動損傷機理不清，且缺乏有效的爆破振動監測方法和安全標準，極易造成重大生產事故，直接威脅到城市生命線工程的安全。目前，針對爆破振動下地下管線的振動響應特征及安全控制這一熱點問題，國內外學者通過采用試驗和數值模擬的方法展開了研究，并取得了一些研究成果。FRANCINI 等[1]對采石場爆破周圍的地下管線進行現場爆破試驗，得出了管線可容許應力與起爆藥量和管線壁厚之間關系；王海濤等[2]通過室內相似模型試驗發現相同爆破荷載作用下巖層和管道振動特性存在差異；張黎明等[3-4]對地下DN100 熱鍍鋅鋼管進行現場爆破試驗，發現地表合成峰值振速與地下管線的軸向、環向應變呈指數函數關系，并預測出管道所能承受的地表最大峰值振速；PARVIZ 等[5]發現管道壓力與土體的密度有關，土體密度增大導致管道壓力和主應力增大；張坤等[6]得到了不同爆心距下地下管線的應力峰值；鄭爽英等[7-8]得到了圓形輸氣管道在隧道爆破下的應力變化規律，并通過正交數值試驗研究了管道直徑、壁厚等參數對其動力響應的影響；張震等[9]對比了空管和滿水2種狀態下管道的振動特征，并通過回歸分析得到了管道的爆破控制振速。綜上所述，目前針對隧道近距下穿鋼筋混凝土管線在橫斷面和沿管線縱向的爆破振速和應力響應研究還不夠系統，且沒有考慮凈距、起爆藥量及地層巖性對管線爆破振動響應的影響。本文以北方城市淺埋大跨隧道近距穿越供水管線爆破工程為背景，采用ANSYS/LS-DYNA軟件中的ALE算法建立隧道-地層-管線三維數值模型，分析爆破地震波的傳播規律，研究地下圓形鋼筋混凝土管線在隧道爆破振動下的橫向和縱向振動響應特征，并分析凈距、起爆藥量及周圍地層性質等因素的影響，提出地下供水管線的振動安全標準建議。

1 工程概況及隧道爆破方案

1.1 工程概況

北方城市雙向六車道高速公路東西主線隧道總長約為4 500 m。主線隧道大多為淺埋段，跨度大，三車道斷面跨度為17.00 m；隧道所處地質環境極為復雜，支護方式復雜多變；該隧道工程近距下穿大量供水管線，東主線隧道下穿主要管線6處，管線底部距離隧道拱頂12.68～25.86 m，西主線隧道下穿主要管線4處，管線底部距離隧道拱頂24.82～35.79 m。尤其是其中2 根主要供水管線，對隧道近距爆破振動控制的安全要求極高，必須確保隧道穿越過程中管線的安全。

隧道東線與其中1根最主要的大直徑供水管線的最小凈距僅16.79 m，約為隧道洞徑的1 倍，如圖1所示。該供水管線建于1997年，為鋼筋混凝土有壓管道。圖2所示為管道截面尺寸，管線采用圓形截面，管道內徑為4 m，外徑為5 m，洞身為C30 現澆鋼筋混凝土。下穿段圍巖以Ⅳ級圍巖為主，東線下穿段管線底層巖性為砂卵石土層，西線段則以千枚巖和砂巖為主。

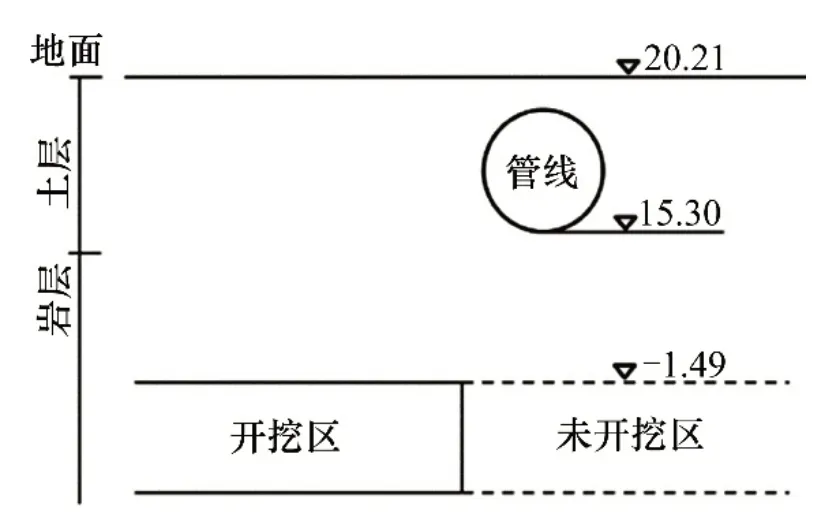
圖1 隧道與供水管線位置關系Fig.1 Position relationship between tunnel and pipeline

1.2 隧道爆破方案

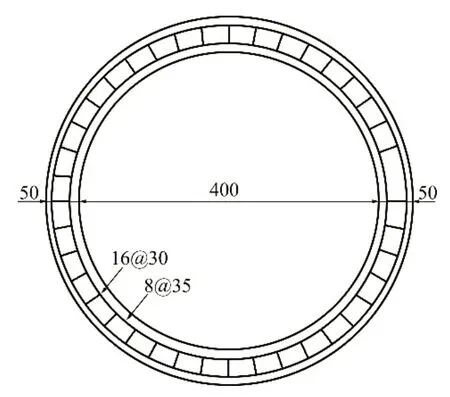
圖2 管道截面尺寸(16@30代表16 mm的鋼筋間距30 cm)Fig.2 Size of the pipeline

工程炸藥選用直徑為32 mm的2號巖石防水乳化炸藥，炮孔直徑為40 mm，起爆形式以非電導爆管雷管起爆為主。采用上、中、下三臺階法進行爆破施工，循環進尺為0.75 m，掏槽孔深度1.0 m。當隧道采用臺階法爆破時，由于上臺階掏槽爆破自由面最少，巖石夾制作用最大，且上臺階距離管線也最近，其引起的爆破地震效應最強，對管線的振動影響也最大，故重點研究隧道上臺階掏槽爆破時引起的管線動力響應。上臺階分為Ⅰ部、Ⅱ部和Ⅲ部進行爆破，炮孔的起爆采用由內向外逐層起爆的爆破順序，依次為掏槽孔、輔助孔和周邊孔，相鄰兩段炮孔的起爆時間嚴格控制在50 ms以上，爆破施工的雷管段位如圖3所示。掏槽孔單孔平均藥量為0.45 kg，輔助眼單孔藥量0.40 kg，周邊眼藥量為0.20 kg。

2 數值模型及其驗證

2.1 數值模型建立

為節約計算成本，以YOZ面為對稱面建立1/2對稱模型，如圖4所示，模型的長×寬×高為20 m×18 m×30 m，單元控制在30 cm 左右。圖5所示為管線混凝土及鋼筋單元。由于掏槽炮孔之間的距離遠小于隧道距管線的距離，采用等效直徑的方法[7]將多個掏槽炮孔簡化為1個炮孔，圓柱形炸藥通 過 INITIAL_VOLUME_FRACTION_GEOMETRY[10]關鍵字建模。鋼筋混凝土采用分離法建模，并通過CONSTRAINED LAGRANGE IN_SOLID[10]關鍵字進行節點耦合。土層與管線之間采用面面自動約束，與巖層之間才采用共節點的方式。在模型對稱面施加對稱約束，頂面定義為自由面，其余面則定義為無反射邊界[11]。整個數值模型單元總數超過70 萬個，模擬時間為0.3 s，實際求解時間為18 h。

圖3 上臺階爆破施工圖Fig.3 Blasting construction of top bench

圖4 數值模型及單元劃分Fig.4 Finite element model and meshing

2.2 材料模型

2.2.1 空氣

空氣采用MAT_NULL 材料模型和EOS_LINEAR_POLYNOMIAL線性多項式狀態方程進行描述[12]，其壓力P為：

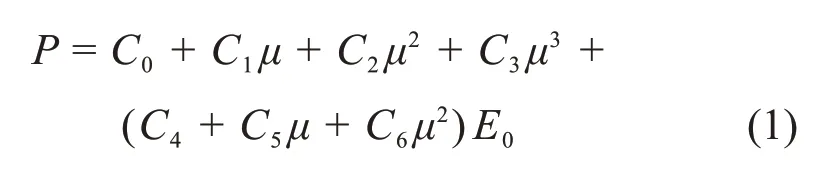
式中：μ為比體積，μ=ρ1/ρ0?1，ρ1為當前密度，ρ0為初始密度；E0為材料的初始比內能；C0，C1，C2，C3，C4，C5和C6為狀態方程參數；V0為初始體積。空氣材料參數如表1所示[13]。

2.2.2 炸藥

炸藥采用MAT_HIGH_EXPLOSIVE_BURN 材料模型，并使用EOS_JWL狀態方程計算壓力[12]：

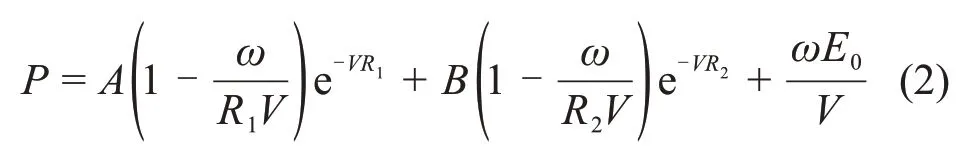
式中：A，B，R1，R2和ω為狀態方程參數；V為相對體積；D為爆轟波波速。對于2 號巖石乳化炸藥，材料參數如表2所示[14]，ρ為密度。

2.2.3 巖層

巖層采用MAT_PLASTIC_KINEMATIC材料模型[12]，該模型廣泛用于模擬巖層在爆炸沖擊下的動態力學行為[15]，根據工程地質勘察報告，該地區巖層以風化砂巖為主，具體參數如表3所示。

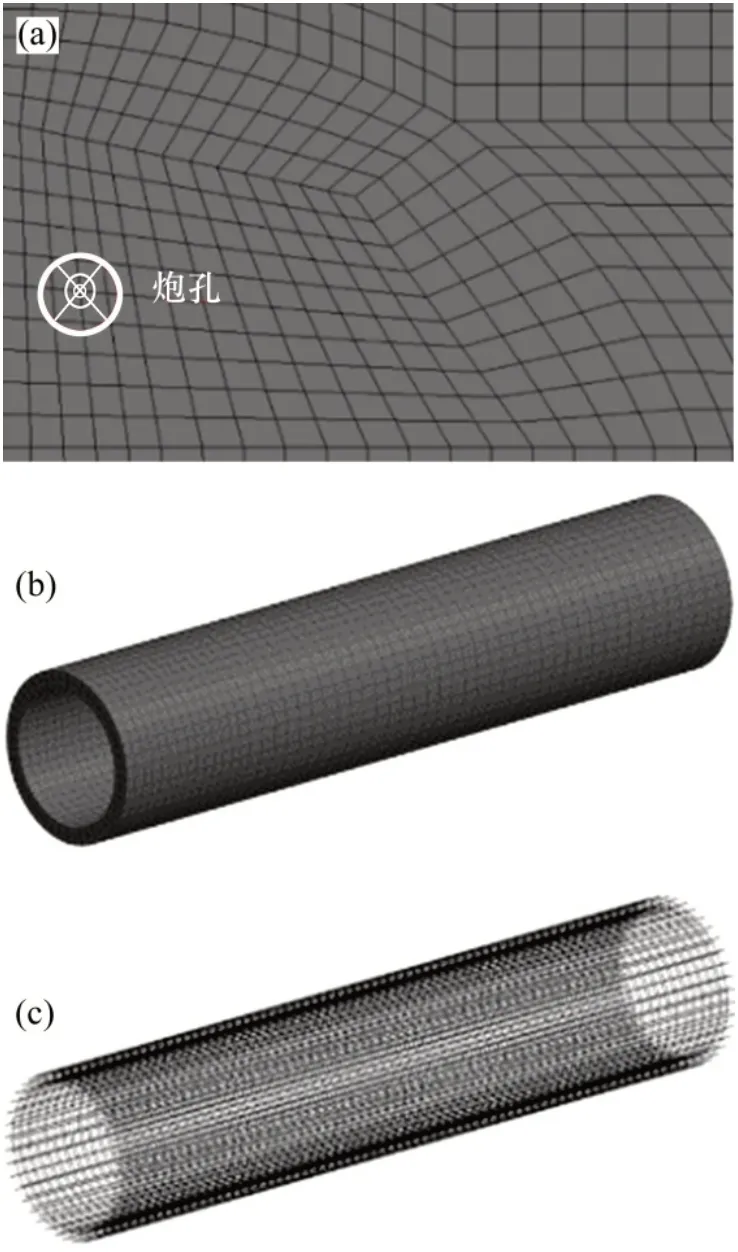
圖5 炮孔、管線混凝土及鋼筋單元Fig.5 Blasting hole,concrete and steel elements

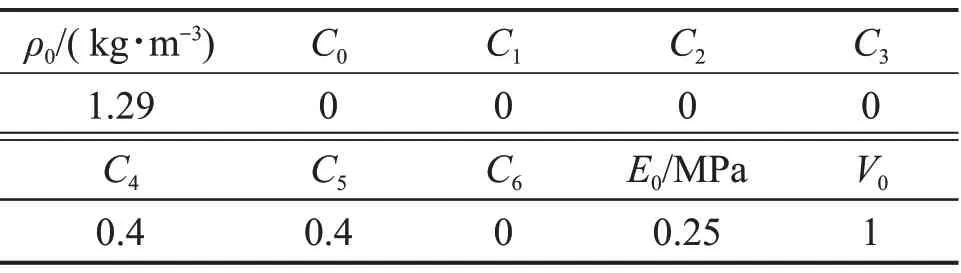
表1 空氣材料參數Table 1 Parameters of air

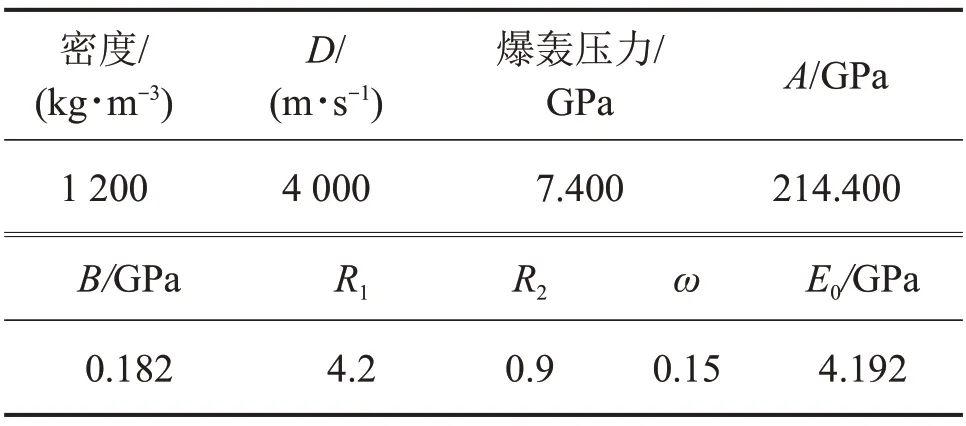
表2 炸藥材料參數Table 2 Parameters of explosive

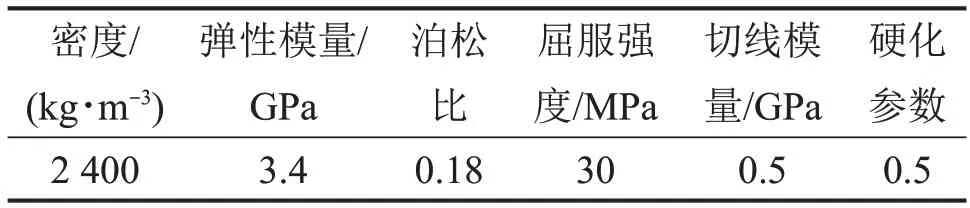
表3 巖層材料參數Table 3 Parameters of rock

2.2.4 土層

土層采用MAT_FHWA_SOIL 模型，采用該材料模型對Mohr?Coulomb準則進行修正，擴展了含水率、應力軟化、運動學硬化和變形率等的影響[12]，適合模擬爆炸問題中的土壤材料[16]。隧道下穿管線段土層大多為含卵石礫砂，其材料參數如表4所示[17]。表4 中：GS為土體相對密度；K為體積模量；G為剪切模量；c為黏聚力；φ為摩擦角；W為含水率。

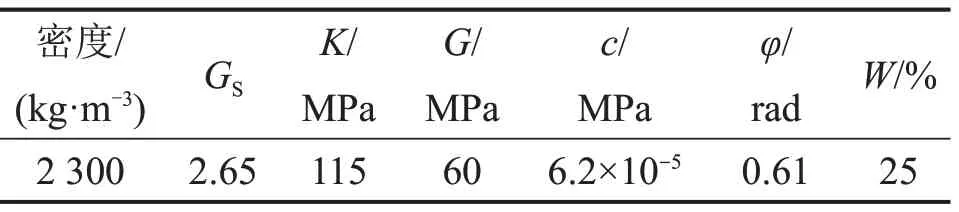
表4 土層材料參數Table 4 Parameters of soil

2.2.5 混凝土材料

地下管線混凝土強度為C30，采用MAT_72R3模型進行模擬。該模型采用3個剪切失效面，考慮了混凝土的損傷和應變率效應，且僅需輸入混凝土的密度ρ、抗壓強度A0和單位換算系數RS和UCF等即可自動生成，能夠較好地模擬混凝土材料在爆炸荷載下的動力響應[18]。C30 混凝土參數如表5所示。

表5 C30混凝土材料參數Table 5 Parameters of concrete of C30

2.2.6 鋼筋材料

地下管線縱筋采用HRB335，抗拉強度為335 MPa，箍筋采用HPB235，抗拉強度為235 MPa，鋼筋采用MAT_PLASTIC_KINEMATIC 材料模型，并按COWPER_SYMONDS方式考慮應變率效應對屈服強度的影響[12]，其中Cs和Ps為應變率系數，用來定義鋼筋材料的動力增大系數，其材料參數見表6[19-21]。

2.3 ALE算法

在隧道爆破模擬中，模型包含巖層、土層、空氣和炸藥等多種物質，為避免計算過程中單元變形過大導致網格畸變，中斷數值計算，故選用ALE 算法進行模擬。ALE 算法先執行1個或幾個Lagrange時步計算，此時單元網格隨材料流動產生變形；接著執行ALE 時步，即保持變形后的邊界條件，在網格拓撲關系不變的前提下對內部單元重新劃分網格，然后將變形網格中的單元變量和節點速度輸送到新網格中。ALE 算法相比Lagrange算法能夠有效地處理大變形問題，同時還能提供比Euler 算法更清晰的界定物質流動的界面[22]。本文將炸藥和空氣劃分為Euler 網格，使用ALE_MULTI-MATERIAL_GROUP關鍵字將它們綁定在同一個單元算法當中；巖層、土層和管道劃分為Lagrange 網格，Lagrange 網格和Euler 網格之間的通過定義CONSTRAINED_LAGRANGE_IN_SOLID關鍵字實現流固耦合[22]。

表6 鋼筋材料參數Table 6 Parameters of steel

2.4 數值模型的可靠性驗證

為了驗證數值模型，本文選取相似試驗段，隧道爆破施工時同時對地表測點進行爆破振動測試，并將現場試驗的實測振速與數值模擬得到的振速進行對比，驗證數值模擬的可靠性。圖6所示為地表測點的布置圖，統計的數值模擬測點和實測測點的峰值振速對比結果如表7所示。

圖6 現場監測及測點位置Fig.6 Field monitoring and location of points

由表7可見：在峰值振速方面，地面3個方向模擬振速與實測振速峰值相對誤差最大為4.8%，小于工程允許誤差5.0%，因此，基于該數值計算模型研究爆破振動下地下管線的動力響應是可靠的。

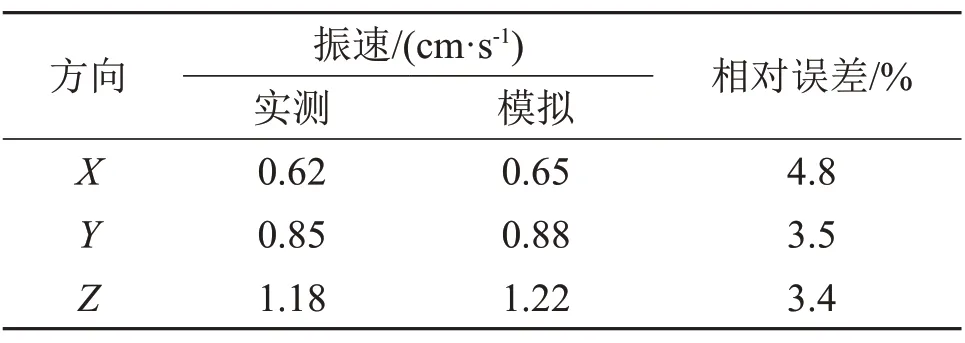
表7 各監測點質點振速對比Table 7 Comparison of particle vibration velocity of monitoring points

3 地下供水管線振動響應

3.1 爆破地震波的傳播

圖7所示為不同時刻巖層介質壓力云圖。由圖7(a)可見：炸藥起爆后，爆破地震波以球面波的形式在巖層中傳播，同時，炮孔周圍巖層被炸裂。隨著爆破地震波的傳播，其波前面積不斷增大，峰值壓力則不斷減小。由圖7(b)可見：當爆破地震波傳播至模型邊界時并未發生反射，可見非反射邊界定義的正確性。由圖7(c)可見：爆破地震波在t=14 ms 時刻傳播至巖層與土層交界處。由圖7(d)可見：地震波在交界處發生反射和透射，一部分發生反射返回巖層向地底傳播，另一部分則透過界面在土層中傳播。

圖8所示為不同時刻爆破地震波在土層中的傳播情況。由圖8 可見：在t=14 ms 時，爆破地震波到達炸藥正上方巖層土層交界處，發生反射和透射；在t=16 ms時，傳播至管線下表面，隨后，爆破地震波同樣在管線與土層交界處發生反射和透射，一部分地震波進入管線，另一部分地震波則繞開管線向地表傳播；大約在t=22 ms時爆破地震波到達地表。

不同時刻爆破地震波在管線上的傳播情況如圖9所示。

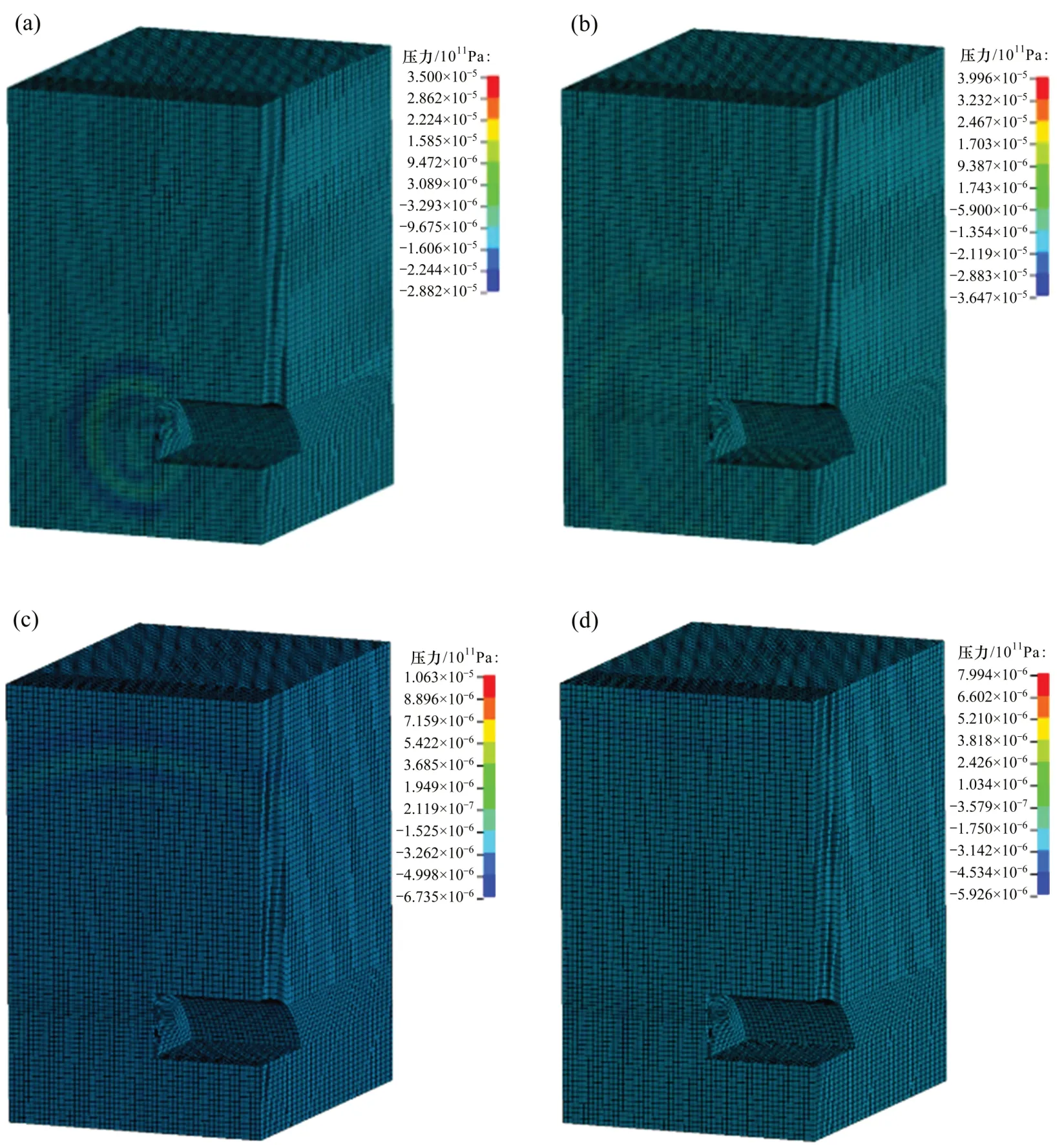
圖7 不同時刻巖層介質壓力云圖Fig.7 Pressures of rock at different times

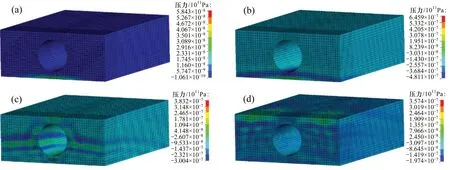
圖8 不同時刻土層介質壓力云圖Fig.8 Pressures of soil at different times

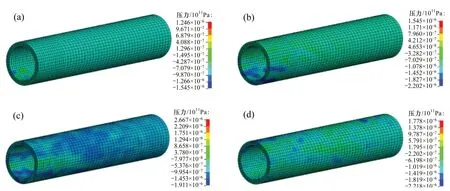
圖9 不同時刻管線壓力云圖Fig.9 Pressures of pipeline at different times

由圖9可見：爆破地震波首先到達炸藥正上方管線底部，使該區域首先受到壓力。隨后，地震波沿管線高度方向和長度方向傳播，管道受到的壓力不斷增大，大約在t=22 ms，圓形管道全部受到爆破地震波的作用。由于地震波在土層、管道和空氣等不同介質傳播時會發生復雜的反射和透射，管道處于反復拉壓狀態。隨著時間的延長，爆破地震波的峰值壓力不斷降低，當其在土中完全衰減后，管線停止響應。

3.2 地下管線的振速和應力響應

在爆破作用下，地下結構受四周巖土介質約束，位移影響通常較小，其振動響應主要通過結構的振速峰值和拉應力進行描述。首先選取炸藥正上方的管線橫截面，對該橫截面上不同部位的單元拉應力峰值和垂直振速峰值進行分析；隨后研究其沿管線縱向方向上的變化，分析傳播規律。圖10所示為管線各部位單元選取示意圖，其中：A為管線頂部中心處位置，B為頂部45°處位置，C為管線中部位置，D為底部45°處位置，E為管線底部中心處位置。

圖10 單元選取及管線長度方向示意圖Fig.10 Diagram of horizontal and vertical elements of pipeline

隧道爆源正上方管線截面(0 m)不同位置處的振速峰值和拉應力峰值如圖11所示。由圖11(a)可見：管線在爆破振動下各部分的振速峰值和拉應力峰值相差較大，其中，管線底部的振速峰值最大，中部次之，頂部的振速峰值最小。E處的振速峰值最大，約2.935 cm/s，其余依次為D，C，A和B處，B處的振速峰值最小，僅為0.764 cm/s，與E處相差3.0倍左右；由圖11(b)可見：管線各部分的拉應力峰值相對較小，均未超過0.2 MPa，而且管線各部分拉應力峰值與振速峰值并無關系，最大拉應力峰值并非出現在振速峰值最大的地方，管線中部的拉應力峰值最大，底部次之，頂部最小。最大拉應力峰值出現在C處，約0.157 MPa，最小拉應力峰值出現在A處，約0.08 MPa，兩者相差近1.0倍。

管線不同部位振速和拉應力峰值沿管線長度方向的變化情況如圖12所示。由圖12可見：管線各部分的振速峰值和拉應力峰值均出現在距離爆源0～4 m 處，并隨著與爆源距離的增大而逐漸減小，且不同截面上各單元之間的振速和拉應力峰值的差值同樣隨著與爆源距離的增大而減小，在爆源正上方管線截面(0 m)上各單元的振速峰值和拉應力峰值相差最大，在距離爆源最遠的管線截面(18 m)上，反而無明顯差異。

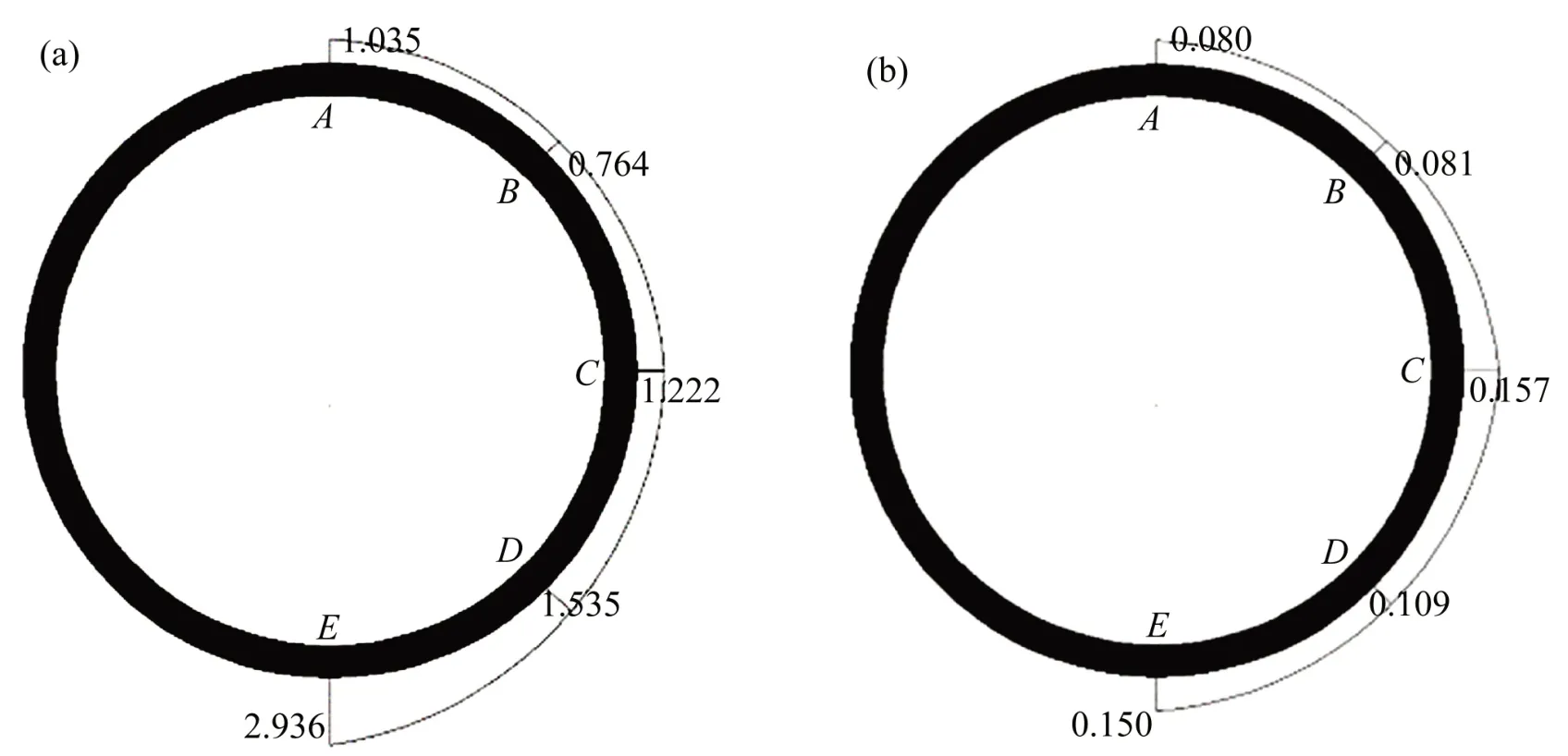
圖11 管線截面不同單元的振速峰值及拉應力峰值Fig.11 Peak value of vibration velocity and tensile stress in different elements of pipeline section

圖12 管線縱向的振速峰值和拉應力峰值變化情況Fig.12 Peak velocity and peak tension stress in longitudinal direction of pipeline

3.3 管線與土層的振動響應差異

隧道爆源正上方的管線截面(0 m)振速和拉應力峰值最大，故選取該截面上管線與土層接觸面頂部、中部和頂部5個位置共計10個單元來分析管道與土層的振動響應差異情況，取點位置如圖13所示，其中：A，B，C，D和E為管線單元，A′，B′，C′，D′和E′為相應的土層單元。

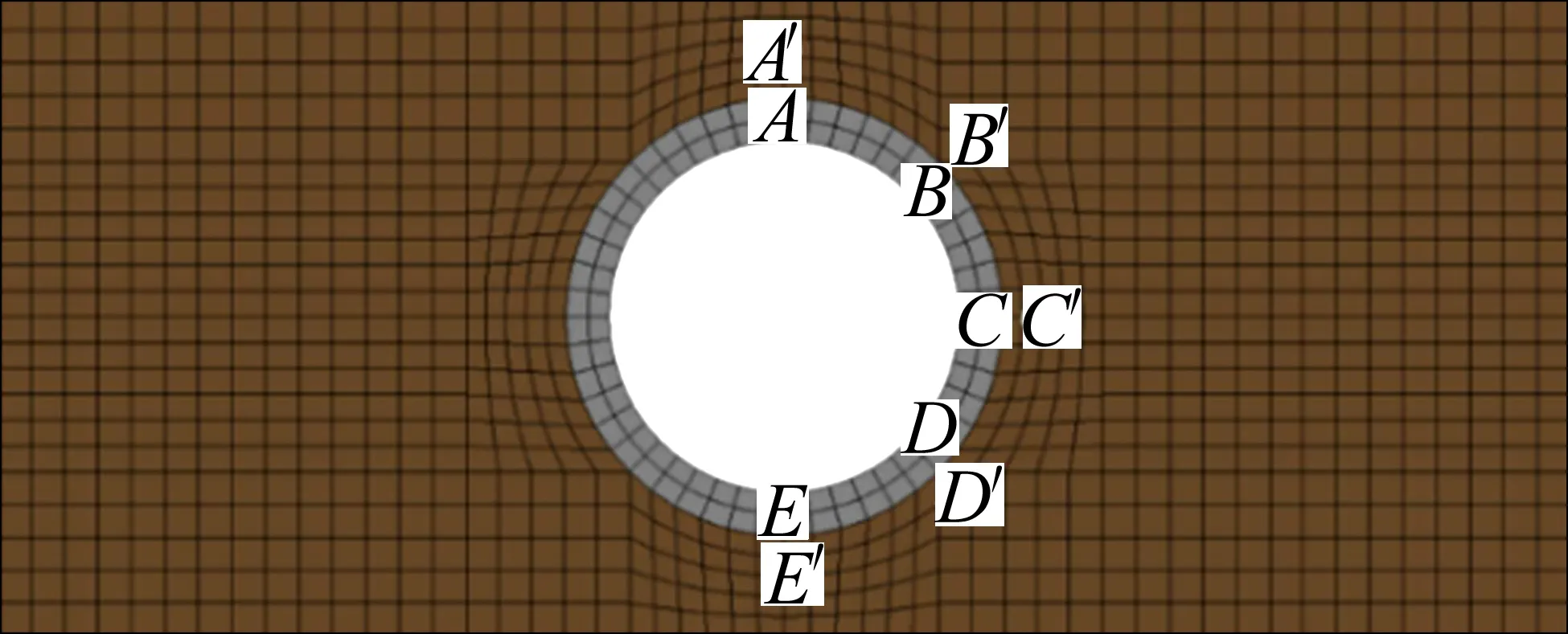
圖13 單元選取示意圖Fig.13 Schematic diagram of elements selection

管線與土層接觸面上各單元垂直方向振動速度時程曲線如圖14所示。由圖14可見：土層截面各單元振速峰值的排序與管線單元一致，最大振速峰值同樣為底部單元，中部次之，頂部的振速峰值最小。通過對比發現，接觸面上管線各單元的振動強度明顯大于相應的土層單元的振動強度，而且管線單元的振動頻率要高于土層的振動頻率。分析土層與管線各部分間的振速峰值差值，差值大致呈現出自管線底部至頂部逐漸減小的趨勢，A，B，C，D和E處振速峰值相差分別為19.2%，15.6%，26.9%，29.7%和50.4%。

圖14 管線與土層橫向的振速變化Fig.14 Vibration velocity in transverse direction of pipeline and soil

管線與土層接觸面上各部分振速和拉應力峰值沿管線長度方向的變化如圖15所示。由圖15可見：土層各單元的振速峰值和拉應力峰值同樣隨著與爆源距離的增大而減小，而且振速峰值與管線振速峰值之間的差值明顯小于拉應力峰值之間的差值。土層單元E'處的振速峰值與相對應的管線單元相差較大，而A′，B′，C′和D′處除在爆源正上方截面(0 m)相差較大以外，其余截面相差較小；土層各單元的拉應力峰值與管線相比差距明顯，而且兩者間的差值沿管線長度方向逐漸減小。

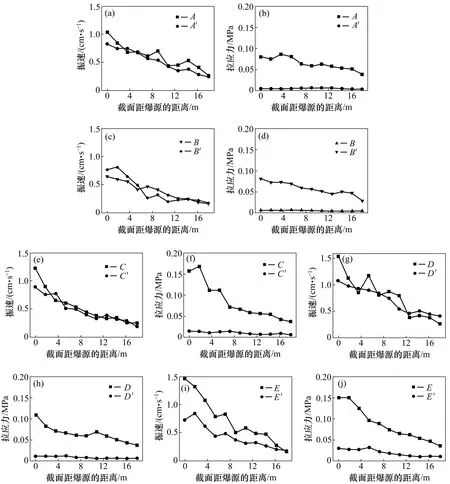
圖15 管線與土層縱向的振速與拉應力峰值變化情況Fig.15 Peak velocity and peak tension stress in longitudinal direction of pipeline and soil

4 不同工況下地下管線振動響應

考慮隧道與管線之間的凈距、掏槽孔的起爆藥量和管線周圍巖土介質的不同，分析隧道爆破振動下管線的不同振動響應，不同工況如表8所示。

4.1 管線與隧道不同凈距對管線振動響應的影響

凈距的影響主要考慮工況1，2，3和4，地下管線在不同凈距下的振速峰值和拉應力峰值變化情況如圖16所示。由圖16可見：圓形管線各部位的振速和拉應力峰值都隨著凈距的縮小不斷增大；凈距的減小不會改變最大振速峰值和拉應力峰值出現的位置；在振速峰值方面，E處的振速峰值總是最大的，而最小振速峰值的部位為B或A處。在拉應力峰值方面，最大應力峰值總是出現在C處，A或B處的峰值拉應力最小。隨著凈距的改變，各部分的增量卻不一致，總體來說，圓形管線上半部分的振速峰值和拉應力峰值的增量要小于其他部分，說明減小凈距對管線上半部分的影響較小，對管線中部和底部影響較大。

表8 不同的分析工況Table 8 Different analysis conditions

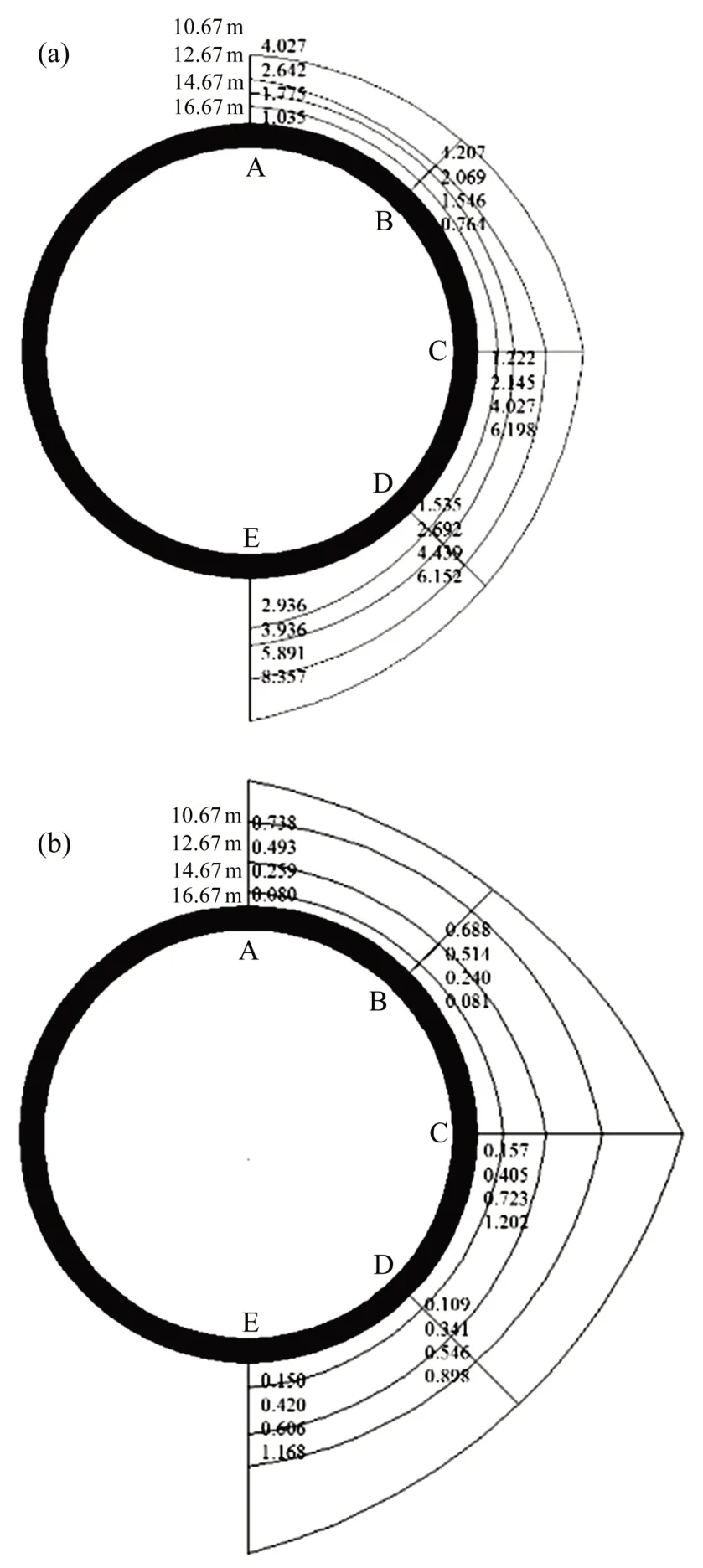
圖16 管線在不同凈距下的振速峰值和拉應力峰值Fig.16 Peak velocity and peak tension stress of pipeline under different space between tunnel and pipeline

4.2 掏槽孔起爆藥量對地下管線振動響應的影響

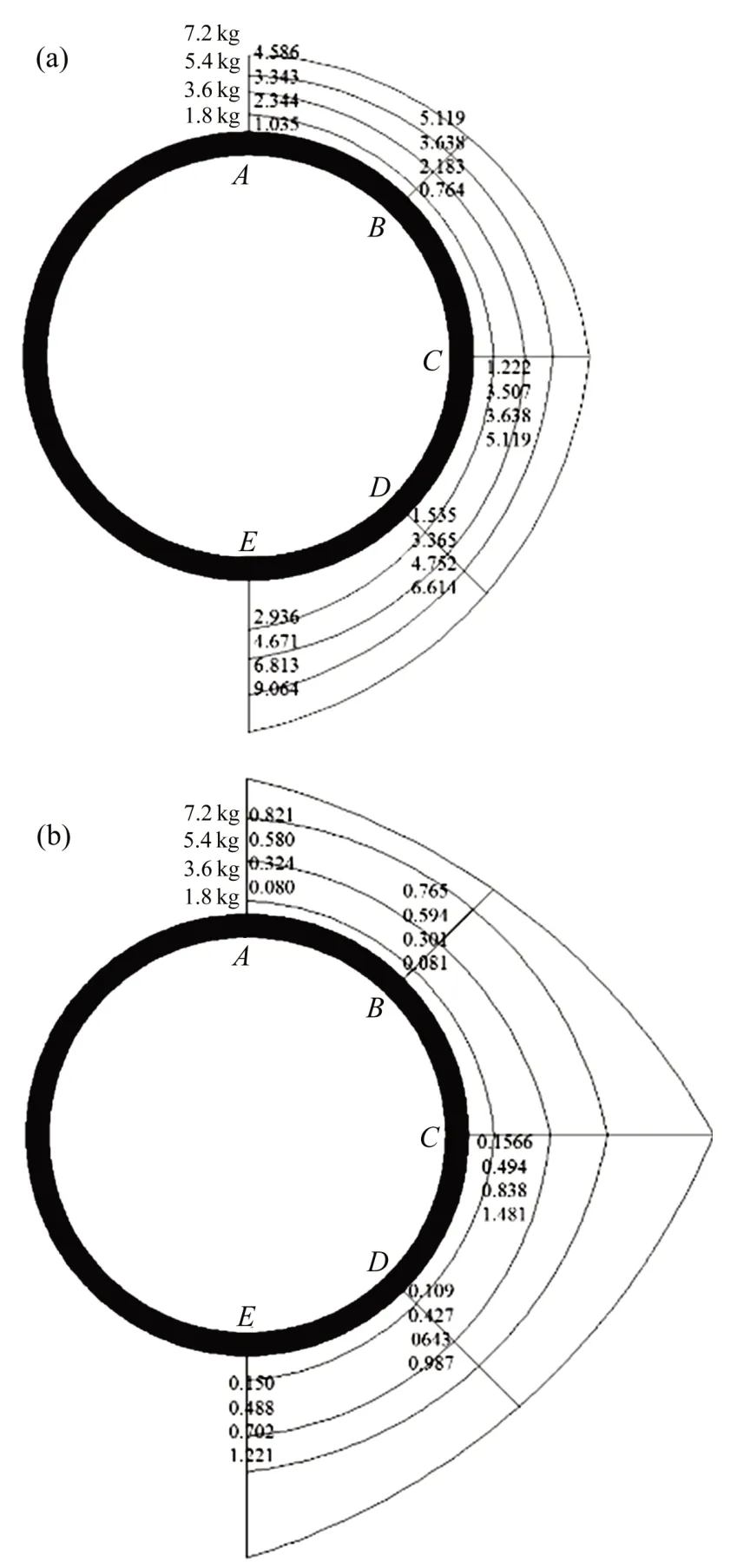
圖17 管線在不同藥量下的振速峰值和拉應力峰值Fig.17 Peak velocity and peak tension stress of pipeline under different charges

掏槽孔起爆藥量的影響主要考慮工況1，5，6和7，圓形管線在掏槽孔不同起爆藥量下的振速峰值和拉應力峰值變化情況如圖17所示。由圖17可見：圓形管線各部位的振速和拉應力峰值都隨著藥量的增大不斷增大。藥量的增大沒有改變圓形管線最大振速峰值和拉應力峰值出現的位置，在振速峰值方面，E處的振速峰值總是最大，而最小振速峰值的部位則由B處變為A處。在拉應力峰值方面，最大拉應力峰值總是出現在C處，B處的拉應力峰值最小。而隨著藥量的改變，各部分單元的增量卻不一致，總體來說，圓形管線上半部分的振速峰值和拉應力峰值的增量要比其他部分的小，說明藥量的增大對圓形管線上半部分的影響較小。

4.3 周圍地層對地下管線振動響應的影響

在爆破振動下管線周圍巖土介質也會對管線的振動響應造成影響。選取爆源正上方的管線截面(0 m)振速和拉應力峰值，分析周圍巖土介質對爆破振動下地下管線振動響應的影響，主要考慮工況1，8和9，材料參數均取自文獻[23]，詳見表9。

管線在不同土層中的振速峰值和拉應力峰值變化情況如圖18所示。由圖18可見：管線各部分受到土層類別的影響程度不同，地下管線周邊為含卵石砂層時，管線的峰值振速和峰值拉應力最大，地下管線周邊為回填黏土和夯實砂土時則較小；中、下部分的振速峰值和拉應力峰值相差較大，而上半部分受影響較小。但土層類別并沒有改變圓形管線中最大振速峰值和拉應力峰值的出現位置，最大振速峰值總是在E處，最大拉應力峰值總是在C處。圓形管線在土層一中的振速峰值和拉應力峰值最大，土層二的次之，土層三的最小。

5 管線振動安全標準

爆破振動作用下地下結構的損傷往往是由局部構件的應力超過材料強度所致。振動下建(構)筑物控制方法較多[24-27]，對于隧道爆破爆破振動下，以控制振速為主。通過上述分析，管線C和E處的拉應力峰值較大，為易受損部位，但C處的峰值振速要小于管線E處。因此，將C處的振速峰值作為判斷整個管線的爆破振速安全控制標準。對圖12中C處單元的振速峰值和拉應力峰值進行分析，從統計學的角度研究兩者間的函數關系[28-30]。

表9 土層材料參數Table 9 Parameters of soil

圖18 管線在不同土層中的振速峰值和拉應力峰值Fig.18 Peak velocity and peak tension stress of pipeline under different soil medium

圖19所示為管線拉應力峰值和振動速度峰值的統計關系，二者之間的關系表達式為：

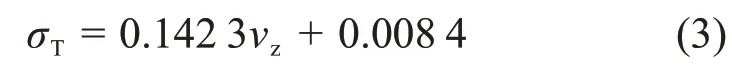
式中：σT為拉應力峰值，MPa；vz為垂直方向的振動速度峰值，cm/s。

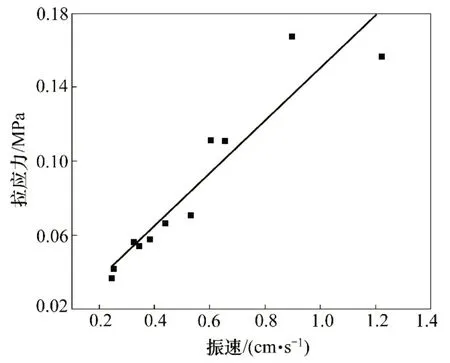
圖19 管線拉應力峰值與振動速度峰值的統計關系Fig.19 Statistical relationship between peak tensile stress and peak vibration velocity of pipeline

在式(3)中，R2=0.876 3，表明管線所受拉應力峰值和振動速度峰值之間存在線性關系。依據管線混凝土的抗拉強度，由最大拉應力強度理論即可得到管道在爆破振動作用下的控制振速峰值，將C30混凝土的抗拉強度標準2.00 MPa[31]代入式(3)可以得到：當管線振動速度峰值為14.06 cm/s 時，所受到的拉應力達到其抗拉強度。考慮到該供水管線修建時間較為久遠，本身已經存在開裂滲水現象，將安全系數設定為3.0[32]，修正后的峰值振速為4.68 cm/s。

6 結論

1)在隧道上方地面進行爆破振動測試，地面3個方向模擬振速峰值與實測振速峰值相對誤差均小于5.0%，驗證了數值模擬的可靠性。

2)在管線橫斷面方向，底部的振速峰值最大，中部的次之，頂部的振速峰值最小；而管線中部的拉應力峰值最大，底部的拉應力峰值次之，頂部的拉應力峰值最小；管線沿縱向峰值均出現在距離爆源0～4 m 處，并隨著與爆源距離的增大而逐漸減小。

3)管線與土層接觸面上管線各單元的振動強度明顯大于相應的土層單元的振動強度，而且管線單元振動頻率要高于土層的振動頻率。

4)管線各部位的振速和拉應力峰值都隨著凈距的縮小、掏槽藥量的增大而不斷增大；地下管線周邊為含卵石砂層時，管線的峰值振速和峰值拉應力最大，回填黏土和夯實砂土時則較小。

5)根據最大拉應力強度理論，建議管線的最大振速控制在4.68 cm/s以下。