復雜條件下的社區搜索方法?

竺俊超,王朝坤

(清華大學 軟件學院,北京 100084)

由大量節點和節點間的連接關系形成的網絡結構廣泛存在于計算機科學、生物學和社會學[1,2]等領域,例如以網頁為節點、以網頁間的鏈接為邊組成的萬維網[3]和以人為節點、以人際間關系為邊建立的社會網[1,2]等.在網絡相關研究工作中,社區(community)的概念持續受到人們的關注.一般而言,社區是指內部節點間聯系較內部與外部節點間聯系更為緊密的子網絡.發現網絡中的各種社區結構有助于進行好友推薦、犯罪團伙識別以及蛋白質功能預測[4-6],同時能夠有效支持網絡中傳播熱點選擇[7]和介數中心度更新[8].

社區搜索(community search)是指給定一個或多個節點,尋找包含它們的社區[9-14].與社區發現(community detection)相比,它更關注局部的網絡結構,能夠返回更加個性化的社區結果.

現有的社區搜索方法包括僅與網絡拓撲有關的社區搜索和與節點屬性有關的社區搜索:前者旨在尋找包含給定節點集且滿足k-clique[9],k-core[10,11]或k-truss[12,13]等特定拓撲結構的社區;后者在尋找包含給定節點集的社區時綜合考慮了拓撲結構和節點屬性[15-17],返回的結果社區不僅要滿足特定拓撲結構,還要使內部節點的屬性盡可能相近.

然而,已有的社區搜索研究成果尚不能滿足人們日益增長的客觀需求.例如,在實際應用中經常會遇到這樣一些問題:如何準確地找到一個社區,使它不僅包含某些給定節點,同時不包含另一些給定節點?如何智能地找到一個社區,至少要包含給定的5個節點中的任意3個?本文將這類包含對節點條件約束的社區搜索問題統稱為條件社區搜索問題(conditional community search,簡稱CCS).據我們所知,目前國內外尚未見針對CCS問題的公開報道.

例1(社交場景):用戶A和B擬共同組建一個學習討論小組,組內成員盡可能互相認識以便討論,且不希望保險推銷員C參與.則A和B可以邀請哪些人加入該小組?

圖1展示了上述社交場景中的部分網絡結構,其中,節點代表人物,邊代表好友關系.若以A和B作為社區必須包含的節點,則依據以 2-core為基礎的社區搜索方法得到的結果社區如實線圈所示.這是因為該社區中每位用戶在本社區內都有至少兩位好友并且該社區僅有兩條從內部連向外部的邊,具有內部節點間聯系較內部與外部節點間聯系更加緊密的性質.但是該社區顯然不滿足節點C不參與的要求.如果應用CCS來計算,即找到一個包含A和B,同時不包含C的社區,那么結果社區如虛線圈所示.這是因為該社區內每位用戶都有至少兩位好友,同時節點C不出現在此社區中.進一步而言,C也很難通過其好友加入到該社區內.因此對于例1,A和B可以邀請虛線圈中的成員組建討論小組.此外,在視頻網站為用戶提供社區推薦、購物網站為用戶提供相關商品推薦等場景下,也會遇到用戶不希望特定的人物或商品出現在推薦列表中的需求.

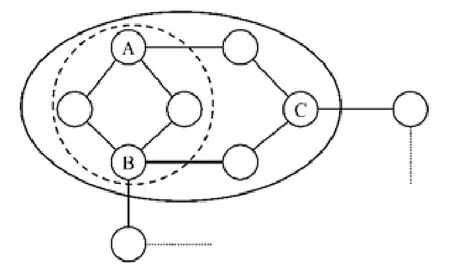
Fig.1 An example for conditional community search圖1 條件社區搜索的示例

例2(商業場景):某公司發生了商業機密泄露事件,內部能夠接觸該機密的有A,B兩人,而競爭對手公司中取得此機密的是C,D兩人.該公司希望對A和B展開調查,找出A或B中至少一人可能與C或D存在的聯系.通過郵件、電話等聯系方式建立了社會關系網絡后,可以通過尋找至少包含A,B中一人、C,D中一人的社區來獲得相關信息.

例 2中的場景對于結果社區提出了一類典型需求,即至少包含給定節點中的任意一個.顯然,傳統社區搜索方法缺乏對該需求的有效支持;借助CCS,可以將上述需求通過布爾表達式的形式清晰地予以表示.

上述實例表明,現有的社區搜索方法難以有效解決迫切的客觀需求.為此,本文提出并研究條件社區搜索問題,給出條件社區搜索的通用框架,嘗試對社交網絡進行智能分析,在復雜的搜索條件下,為用戶提供更好的結果社區.

事實上,傳統的社區搜索問題可以看做是條件社區搜索問題的特例,其中,搜索條件退化為社區中需要包含全部給定節點.需要注意的是:本文關注如何在復雜條件下進行社區搜索來獲得更加符合實際需求的結果社區,而未涉及新社區結構的設計,即現有的社區結構都可以應用到條件社區搜索中來.

本文的主要貢獻包括:

(1) 提出條件社區搜索這一新問題,并給出其形式化定義;

(2) 提出條件社區搜索的通用框架,并對其中的單項條件社區搜索步驟給出“社區搜索+過濾”的方法和基于標簽傳播給點加權的方法(weighting by label propagation,簡稱WLP);

(3) 在真實數據集上進行了大量實驗,實驗結果驗證了所提方法的正確性和有效性.

本文第 1節介紹相關工作,包括社區發現和社區搜索的一般方法.第 2節給出條件社區搜索問題的形式化定義、解決該問題的通用框架和搜索條件的簡化策略.第 3節提出對于單項條件社區搜索的解決方法.第 4節報告并分析實驗結果,包括對搜索條件簡化的有效性驗證以及“社區搜索+過濾”方法和 WLP方法在時間開銷和社區結果質量上的比較.第5節總結全文.

1 相關工作

本節介紹社區發現和社區搜索的概念,并簡要回顧解決這兩類問題的方法.

1.1 社區發現

社區發現,亦稱為全局社區發現(global community detection),指找出給定網絡圖中的所有社區.社區這一概念尚沒有統一的形式化定義,目前研究工作中的社區定義一般依據特定拓撲結構或者描述子圖緊密程度的度量指標給出.社區發現的常用方法主要包括劃分、聚類、標簽傳播等[18].

劃分方法指通過刪除網絡圖中的一些邊,將原圖自然地分成若干個連通分量來得到社區結果.Kernighan-Lin算法[19]要求最大化社區內節點連邊數量與不同社區間節點連邊數量的差值.SCD算法[20]要求刪除不屬于任何三角形的邊.KMF算法[21]則要求刪除兩端點共同鄰居節點的個數少于給定閾值的邊.

聚類方法包括層次聚類、譜聚類、k-means聚類等.層次聚類通過自上而下不斷刪除邊或者自下而上不斷加入點的方式得到網絡圖的層次結構,然后切分該結構來得到社區.典型方法包括 Fast-Newman[22],CNM[23],Radicchi[24],GN[25],MSG-VM[26]和DOC[27]等.譜聚類通過將網絡表示為特定的拉普拉斯矩陣,基于同一社區內的節點在矩陣中特征向量近似的思想進行聚類[28-30].k-means聚類是常見的聚類方法.在社區發現問題中,常用點和點之間的距離[31]、Random Walk[32,33]等方式給出兩點間相似度量,接著采用k-means聚類進行社區發現.近年來還涌現出基于深度學習的聚類方法,即學習網絡節點的低維向量表示,再通過聚類得到社區,如 CoDDA[34],DeepWalk[35]和 GraRep[36]等.

標簽傳播方法通常為網絡中的每個節點賦予初始標簽,接著模擬信息傳播過程為每個節點更新標簽,最后通過標簽分布確定社區歸屬.基于標簽傳播思想的典型方法包括LPA[37],HANP[38]和SLPA[39]等.

1.2 社區搜索

社區搜索也稱局部社區發現(local community detection).給定一個或多個節點,社區搜索旨在尋找包含這些節點的社區.由于關注局部網絡結構,社區搜索能夠高效地找到用戶關心的節點所在的社區.目前常見的社區搜索算法主要基于k-clique[9],k-core[10,11]和k-truss[12,13]等特定結構.例如,Cui等人提出了尋找包含一個給定節點的k-core社區的問題(CST)和對應算法[11].該算法從給定節點向外擴展得到結果社區.Huang等人提出了基于k-truss的社區定義,并設計了TCP-index來尋找包含某個給定節點的社區[12].

此外還有一類結合拓撲結構和節點屬性的社區搜索方法[15-17].例如:Shang等人根據節點在拓撲結構和屬性上的相似關系構建一個TA-graph,并在此基礎上提出與節點屬性相關的社區搜索算法AGAR[15];Fang等人在k-core結構基礎上要求社區內節點共享盡可能多的標簽屬性,設計了對應索引結構 CL-tree[16];Huang等人在k-truss結構的基礎上設計了一個打分函數來度量給定節點屬性在社區內的流行程度,并提出Attribute Truss社區定義[17].

2 條件社區搜索

條件社區搜索問題不僅要能夠描述社區必須包含給定節點這一基本搜索條件,還要能夠描述兩種新的搜索條件:一是社區不允許包含給定節點,二是社區至少要包含若干給定節點中的一個.本節首先基于布爾表達式給出搜索條件的形式化表達,接著提出條件社區搜索通用框架,最后給出搜索條件的簡化方法.

2.1 搜索條件的形式化表達

布爾表達式是由布爾變量和邏輯運算符組成的式子.布爾變量的取值為真或假,亦可用1或0來表示.邏輯運算符包括與(∧)、或(∨)、非(?)等.在每個布爾變量的取值確定后,可以判斷整個布爾表達式的真假.于是,可以考慮用布爾表達式表示搜索條件.

2.1.1 搜索條件的表示形式

通常,對于一個給定社區,一個節點是否存在于該社區中可以表示為一個布爾變量.若節點存在于該社區中,則對應布爾變量取值為真;反之為假.本文將指代節點的布爾變量稱為節點變量.借助節點變量和邏輯運算符構成的布爾表達式,可以有效表示條件社區搜索問題中的具體搜索條件.

定義1(基本搜索條件).基本搜索條件規定為:

(1) 單個節點變量X是基本搜索條件;

(2) 如果X和Y是基本搜索條件,那么X∧Y是基本搜索條件;

(3) 當且僅當有限次地應用條件(1)和條件(2)所得到的布爾表達式稱為基本搜索條件.

定義2(搜索條件).搜索條件規定為:

(1) 單個節點變量X是搜索條件;

(2) 如果X是搜索條件,那么?X是搜索條件;

(3) 如果X和Y是搜索條件,那么X∧Y,X∨Y是搜索條件;

(4) 當且僅當有限次地應用條件(1)～條件(3)所得到的布爾表達式稱為搜索條件.

本文將滿足定義2但不滿足定義1的布爾表達式稱為復雜搜索條件.

例3:例1中的搜索條件可表示為A∧B∧?C.該布爾表達式在變量A和B為真,且C為假時取真值,對應包含節點A和B但不包含節點C的社區.例2中的搜索條件可表示為(A∨B)∧(C∨D).該布爾表達式在變量A或B為真,且C或D為真時取真值,對應包含A,B中某一人和C,D中某一人的社區.

以上實例表明,布爾表達式能夠有效表示搜索條件.同時,也容易根據社區中是否包含某個節點得到對應變量的值,從而驗證搜索條件.接下來給出條件社區搜索問題的形式化定義.

定義3(條件社區搜索問題CCS).給定連通圖G=(V,E)和節點集V′?V,尋找至少一個滿足如下條件的節點集H:(1)H?V;(2)G[H]是連通的,其中,G[H]表示H的導出子圖;(3)H滿足定義在V′上的搜索條件F;(4)H滿足用戶給定的社區定義?.

其中,搜索條件F按定義2給出,?可以按用戶需求進行指定,例如基于k-core[10,11]或k-truss[12,13]的社區定義.

事實上,CCS包含了現有的社區搜索問題.易知有如下引理.

引理1.社區搜索問題是條件社區搜索問題的特例.

這是因為當搜索條件F為基本搜索條件,即F中僅包含節點變量和邏輯與(∧)時,可以把F涉及的節點合成一個節點集作為社區搜索算法的輸入.此時,條件社區搜索問題就退化成社區搜索問題.

2.1.2 條件社區搜索的通用框架

條件社區搜索的通用框架將用戶給定的條件社區搜索問題分解為若干單項條件社區搜索(single conditional community search,簡稱 SCCS)分別處理,而后進行結果匯聚.需要注意的是,盡管條件社區搜索存在一種樸素的解決方法——首先對給定網絡進行全局社區發現來得到所有社區,接著判斷每個社區是否滿足搜索條件,最后留下滿足搜索條件的社區,但是該方法需要找到全部社區,時間開銷巨大.

定義4(單項條件社區搜索SCCS).對于一個條件社區搜索問題,如果有且僅有一組節點變量的取值能滿足它的搜索條件F,則稱其為單項條件社區搜索.

定理1.任意一個單項條件社區搜索的搜索條件等價于一個合取式(僅由邏輯與運算符連接節點變量或其否定構成的式子).

證明:因為只有一組能滿足搜索條件的節點變量取值,所以每個節點能否存在于社區中是唯一確定的.于是可以構造這樣一個等價合取式:先用邏輯非修飾不允許出現在社區中的節點變量,而后用邏輯與連接所有節點變量. □

給定一個搜索條件,可以先枚舉各節點變量的可能取值,計算得到一個真值表,從而找出所有能滿足搜索條件的節點變量取值組合.用1和0分別代表節點是否存在于社區中,于是,滿足例1中搜索條件的節點變量組合僅有 1組,即A=1,B=1,C=0,例 2則有 9組.接著,對每一種取值組合嘗試找到對應的單項社區搜索的結果.最后,將每個單項社區搜索的結果合并,就能得到條件社區搜索的結果.

綜上,可以歸納出三階段的條件社區搜索通用框架.

(1) 枚舉所有滿足條件的節點變量取值組合;

(2) 將每一個組合對應的合取式作為單項條件社區搜索的條件輸入并執行;(3) 合并所有單項條件社區搜索的結果.

2.2 條件社區搜索問題的復雜性

條件社區搜索問題的復雜性和給定的社區定義及搜索條件有關.通常情況下,CCS是NP完全的.

由引理1,在基本搜索條件下,CCS退化為社區搜索問題.許多傳統的社區搜索問題已被證明是 NP完全的,例如尋找滿足k-core定義的最小社區的問題(mCST)[11].

此外,若把連通子圖作為社區定義,則CCS是NP完全的.這是因為CCS的結果能夠在多項式時間內驗證,是一個NP問題;同時,布爾邏輯的可滿足性問題(SAT)可以歸約到CCS上.歸約的方法是以布爾表達式的所有變量對應的節點構造一個完全圖,將布爾表達式直接對應于搜索條件.此時,CCS每產生一個結果就等同于找到一組滿足布爾表達式的解.

這意味著對于上述幾類CCS問題很難找到快速有效的多項式時間算法.需要注意的是:并非所有的CCS都是NP完全的,如果能夠在多項式時間內找到所有的社區結構(如k-truss[12]結構就存在多項式時間的算法),那么可以利用逐一驗證搜索條件的樸素方法解決CCS,盡管這樣做的效率較低.

2.3 搜索條件的簡化

因為布爾邏輯的可滿足性(SAT)問題是一個NP完全問題,所以很難對第2.1節提出的條件社區搜索通用框架的第 1步進行優化.在實際應用中,考慮到用戶輸入的節點變量總數一般不會很多,采用枚舉形式尋找滿足搜索條件的變量取值是可行的.若用戶輸入的節點數量較多,則可以使用求解 SAT的快速算法,例如 DPLL[40],GRASP[41]等.注意到通用框架的第2步對每個滿足條件的取值組合都要進行一次單項條件社區搜索,于是考慮改進這一步驟,在一次搜索中同時處理多個變量取值組合,從而減少總搜索次數.

首先,在得到所有滿足搜索條件的變量取值組合后,可寫出與搜索條件等價的主析取范式[42],即對搜索條件進行規范化.例如,用戶輸入的搜索條件是?A∧(B∨C),滿足該式的變量取值組合是:A=0,B=1,C=1;A=0,B=0,C=1和A=0,B=1,C=0,從而把搜索條件規范化為(?A∧B∧C)∨(?A∧?B∧C)∨(?A∧B∧?C).主析取范式是合取式的析取,其中每個合取式包含所有節點變量,對應于一組滿足條件的變量取值,即一次單項條件社區搜索.

接下來,排除主析取范式形式的搜索條件可能存在的冗余.例如,范式(A∧B)∨(A∧?B)可化簡成A,即變量B存在與否對搜索條件不產生實際影響.本文用奎因-麥克拉斯基(Quine-McCluskey,簡稱 QM)算法[43]將主析取范式轉化為等價的最簡與或式,從而消除此類冗余,進而減少單項條件社區搜索次數.由于最簡與或式具有最少的合取式個數,所以根據最簡與或式進行單項條件社區搜索的次數是最少的.

最后,在最簡與或式基礎上進一步發現可以通過提取部分合取式的公共變量來提高搜索效率.以搜索條件(A∧B∧C)∨(A∧B∧D)為例,需要對該最簡與或式中的兩個合取式分別進行一次單項條件社區搜索.容易發現,這兩個合取式里都出現了變量A和B.若將其提取到外部,則該式變形為(A∧B)∧(C∨D),可看做一個合取式與一個析取式的合取.本文將一個合取式與至多一個析取式的合取稱為搜索項;接下來,可以用合取式A∧B作為輸入進行單項條件社區搜索;最后,用析取式C∨D來對搜索得到的社區進行判別,使得所需單項條件社區搜索的次數減1.這種合并公共節點變量、把多個單項條件社區搜索一起進行的操作能夠有效地提高整體搜索效率,減少時間開銷.

為有效提取各合取式中的公共變量,本文采取一種貪心的思想:首先統計每個節點變量在最簡與或式的各合取式中出現的次數,找到出現次數最多的變量;接著,合并含有該變量的所有合取式;而后,用同樣策略嘗試合并剩余合取式,直至不能合并為止.具體提取過程見算法 1,其中,merge方法用于提取若干個合取式的公共節點變量,并合并形成新搜索項.

算法1.提取公共變量GetCommon(searches,v_set).

輸入:合取式集合searches,節點變量集合v_set;

輸出:新的搜索項集合new_searches.

令最簡與或式涉及到的所有變量個數為n,搜索項的數量為x,則算法1進行統計節點變量出現次數的時間復雜度是O(nx),找到出現次數最多的公共變量的時間復雜度是O(n),合并含有該變量的合取式的時間復雜度是O(nx).

結合簡化搜索條件的策略,改進后的條件社區搜索通用框架包括如下步驟:

1. 枚舉所有滿足條件的節點變量取值組合,得出與搜索條件等價的主析取范式;

2. 利用QM算法把主析取范式轉化為最簡與或式;

3. 合并最簡與或式中的公共節點變量;

4. 對于每一搜索項,將其合取式作為單項條件社區搜索的輸入并執行,將其析取式用于結果判別;

5. 合并各單項條件社區搜索的結果.

3 單項條件社區搜索

為解決SCCS,第3.1節首先提出“社區搜索+過濾”的方法,第3.2節給出基于標簽傳播給點加權的方法.

方便起見,本文稱社區中必須出現的節點為必要節點,社區中不能出現的節點為禁止節點.由定理1,SCCS僅需考慮合取式形式的搜索條件.因此,可以根據搜索條件中是否存在邏輯非來把對應的節點集合劃分為一個必要節點集和一個禁止節點集.本文將以這兩個集合作為SCCS的輸入.

由定義3可知,CCS需要給定社區定義?.在相關研究中,基于k-core的社區定義是一種比較常見的方式[10,11],于是,本節基于k-core定義來介紹所提方法.顯然,對其他社區定義,本文所提方法亦可修改適用.

定義5(k-core社區).給定圖G=(V,E)和常數k,節點集H?V,稱H為k-core社區,當且僅當H的導出子圖G[H]連通且min{degG[H](v)|v∈H}≥k.

3.1 “社區搜索+過濾”的方法

針對社區搜索算法沒有考慮禁止節點的情況,本節提出預先搜索社區(search-first,簡稱SF)、預先過濾節點(filter-first,簡稱FF)和搜索時篩出(on-the-fly,簡稱OTF)等3種不同策略.這3種策略都采用“社區搜索+過濾”的形式,即:用必要節點進行社區搜索,用禁止節點進行過濾.三者的區別在于,過濾步驟分別安排在社區搜索之后、之前和過程中.

3.1.1 基于k-core的社區搜索方法FindCore

為便于說明“社區搜索+過濾”方法的3種不同策略(SF,FF和OTF),本小節提出基于k-core的社區搜索算法FindCore(見算法2),用于3種策略的社區搜索步驟.

算法2.基于k-core的社區搜索算法FindCore.

輸入:G=(V,E),v_set,k;

輸出:包含v_set的k-core社區C.

FindCore算法從輸入節點集出發,通過從鄰居節點集中選取合適的節點進行擴展,得到k-core社區.首先判別社區的連通性要求,計算當前節點集導出子圖的連通分量(算法2第2行),優先加入連接最多連通分量的節點(第17行、第18行和第21行、第22行).其次,增加當前節點集的最小點度數,優先加入與當前節點集連接數最多的節點.若連接數相同,則優先加入度數最大的節點(第19行、第20行和第23行、第24行).重復擴展過程,直至當前節點集成為連通的k-core社區.需要注意的是:為保證算法的正確性,在加入點的過程中需檢查新增節點的度數(第6行、第7行和第27行),如果新增節點在原圖中度數小于k,那么它不可能是k-core社區的一員.同時,通過循環終止條件保證了結果社區滿足k-core要求(第 9行).此外,設置了搜索節點個數的上限search_limit(第13行),以便提前終止局部搜索的過程.這一設置是為了在搜索條件所要求的k-core社區可能不存在時,防止無謂的節點遍歷.當局部向外擴展的方法找不到合適的k-core社區時,調用global_search方法(第 34行),即從全局出發不斷迭代,刪除度數小于k的節點的方法來尋找k-core社區.文獻[11]中的引理2保證了這一步驟的正確性.

例4:令圖2為當前網絡,取k=2,社區搜索輸入的節點集為{A,B,C,D}.算法2首先計算輸入節點集導出子圖的兩個連通分量{A,B}和{C,D}.接著,將鄰居節點{E,F,G}加入候選集.由于點G與兩個連通分量相連,而E和F各連接一個,于是,點G在第 1次擴展時加入節點集.然后,點E和F依次加入,從而增加了最小節點度數.最終,得到了{A,B,C,D,E,F,G}這一2-core社區.

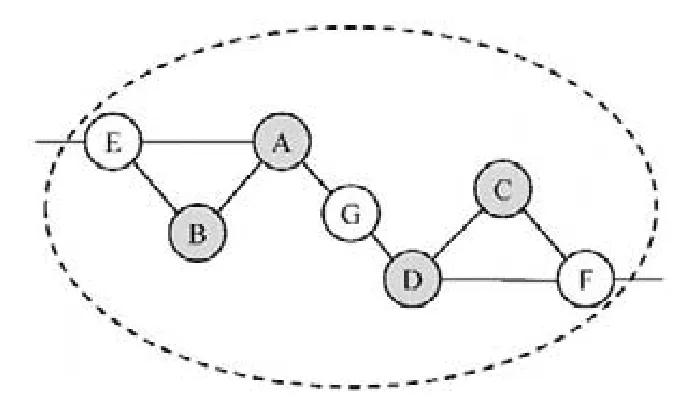
Fig.2 An example fork-core based community search圖2 社區搜索的示例

算法2的時間復雜度是O(m+n),其中,m為邊數量,n為節點數量.這是因為算法在最壞情況下可能要遍歷所有節點和邊.

3.1.2 預先搜索的策略

本小節介紹預先搜索(SF)的策略,其過程分為3步:(1) 用必要節點進行社區搜索得到社區結果;(2) 檢查結果內部是否存在禁止節點,若存在,則刪除其中的禁止節點;(3) 檢查剩余社區結果是否還滿足社區定義,若不滿足,則需調整剩余社區結果.一種通用調整方式是把必要節點作為輸入在剩余社區上再進行一次社區搜索.此外,也可以針對特定社區定義設計調整方案.

以FindCore算法為例,SF先用該算法得到初始k-core社區,再檢查社區內的禁止節點.如果沒有找到禁止節點,就可以直接將它作為結果返回.反之則刪除禁止節點,檢查社區是否還滿足k-core定義:如果不滿足,則可以通過依次刪除社區內度數最低的節點來調整社區結構,嘗試得到k-core社區.

需要注意的是,該策略可能在某些情況下得不到結果社區.以4-core作為社區定義,假設通過預先搜索得到了一個4完全圖結構的社區結果,如果其中含有3個禁止節點,那么社區剩余部分僅有1個節點,無法再得到合理社區結構.因此,該策略有一定的局限性,在實驗中被視作其他方法的基準.

3.1.3 預先過濾的策略

本節介紹預先過濾(FF)的策略,其過程分為2步:(1) 刪除網絡圖中所有禁止節點;(2) 用必要節點集作為輸入,在剩余網絡圖上進行社區搜索.因為在第 1步過濾了禁止節點,所以保證了第 2步得到的社區能滿足搜索條件.

FF策略的缺點是可能存在不必要的節點刪除操作.若禁止節點原本就遠離最終的結果社區,則不需要在社區搜索的過程中對其進行訪問.尤其是當網絡圖規模較大且禁止節點較多時,這類不必要的刪除操作就會影響時間開銷.原因在于,從圖中刪除一個節點會涉及對節點自身及鄰接邊的訪問.

3.1.4 搜索時篩出的策略

本節介紹搜索時篩出(OTF)的策略,即:在社區搜索過程中避開禁止節點,不再需要對結果進行檢查,直接得到符合搜索條件的社區.

以FindCore算法為例,用in_set和out_set分別表示必要節點集和禁止節點集,算法3給出了應用OTF策略的FindCore算法偽碼.它在算法2的基礎上僅修改了第1行、第20行和第34行.其中,第1行避免了將禁止節點加入候選集,第20行消除了禁止節點的度數貢獻,第34行的global_search′方法在迭代刪除度數小于等于k的節點前先刪除了禁止節點.于是,算法3保證了得到的k-core社區能滿足搜索條件.

算法3.基于OTF策略的FindCore算法.

輸入:G=(V,E),in_set,out_set,k;

輸出:社區C(in_set?C,out_set∩C=?).

與前兩種策略相比,OTF策略修改了社區搜索算法,以便在搜索過程中檢查禁止節點.該策略在保證得到正確結果的同時還排除了冗余的刪除操作,因此相比而言更為高效.此外,基于FF策略和OTF策略使用FindCore算法得到的社區結果相同,易證得如下定理:

定理2.使用FindCore算法,通過FF策略和OTF策略所得單項條件社區搜索的結果是相同的.

證明:假定給出合理的單項搜索條件,即,從條件中得出的必要節點集和禁止節點集不相交.首先,在候選集節點提取過程中,FF策略下禁止節點被預先刪除而不會進入候選集,而在 OTF策略下,禁止節點會在候選集擴展時被過濾掉,因此兩種策略下的候選集相同.其次,在從候選集選取優先加入的節點的過程中,FF策略里點的度數是刪除禁止節點后計算的,這一度數與OTF策略下統計的不在禁止節點集中的鄰居節點個數是相等的,因此兩種策略下,每次候選集中選出的最優節點是一樣的.綜上,這兩種策略得到的社區結果是相同的. □

3.2 基于標簽傳播思想給點加權的方法

例5:如圖3所示,一個示例網絡中的節點代表個體,邊表示好友關系.假定個體A擬建立一個不包含B的討論小組,于是對應的CCS為尋找滿足搜索條件A∧?B的社區,即A為必要節點、B為禁止節點.若以3-core作為社區結構,則通過“社區搜索+過濾”的方法(FF策略)得到的一個社區結果為虛線包圍的子網絡.因為該社區中的B1～B3和B都是好友關系,所以B有可能通過其中的某個/些好友了解該討論小組的情況,而這是A所不希望的.

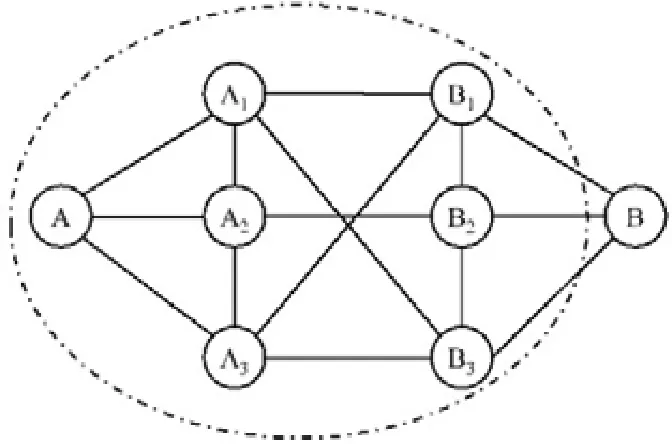
Fig.3 Result of community+search method (FF)圖3 FF策略下“社區搜索+過濾”方法的結果

例5表明,“社區搜索+過濾”的方法得到的社區雖然能夠滿足社區定義和搜索條件,但是難以體現出社區中的節點應盡量遠離禁止節點,同時盡量靠近必要節點的潛在需求.簡便起見,文中以傾向性指代節點相對于必要節點和禁止節點的接近程度.一個節點離禁止節點越遠、離必要節點越近,則該節點的傾向性越大.本節提出了基于標簽傳播給點加權的方法(WLP),用節點的權重來表示節點的傾向性.

3.2.1 基于標簽傳播的加權過程

利用標簽傳播進行社區發現的方法包括以下步驟:首先為每個節點賦予唯一的初始標簽,接著逐輪迭代,把每個節點的標簽迭代更新為其鄰居節點中出現次數最多的那一個.經過數輪迭代后,最終把標簽相同的節點歸入同一社區.

基于上述思想,本節提出一種為節點加權的方法.初始時,先將節點權重設置如下:

接著對節點的權重進行迭代更新,但保持必要節點和禁止節點的權重固定不變.一個節點的新權重決定于其所有鄰居節點的上一輪權重.為了使得新權重落在[-1,1]區間內,以如下方式更新權重:

其中,N(v)表示節點v的鄰居節點,Wi(v)表示節點v的第i輪權重.在第1輪迭代中,必要節點和禁止節點的一跳鄰居被賦予新權重.此時,與較多必要節點相連的節點權重變大,和較多禁止節點相連的節點權重變小,體現出各自的傾向性大小.在第γ輪迭代中,這種傾向性會傳遞給必要節點和禁止節點的γ跳鄰居.

接下來,通過給定閾值λ排除權重小于λ的節點,這樣可以去除那些不宜出現在社區中的傾向性較小的節點.經過閾值篩選后的節點所形成的導出子圖可能不滿足任何的社區定義,為此,在最后需要調整該子圖的結構,例如通過FindCore算法在該子圖里尋找k-core社區.綜上,WLP方法分為如下3個步驟.

(1) 按標簽傳播的方式為各個節點賦予權重;

(2) 以給定閾值篩選出權重較大的節點;

(3) 在篩出節點集的導出子圖上進行社區搜索.

相對于“社區搜索+過濾”方法,WLP方法強調了條件中必要節點和禁止節點對周圍節點的影響,排除了那些與禁止節點過近的節點,保留了與必要節點更接近即傾向性更大的節點.

WLP方法如算法4所示,其中,第2行～第15行是權重賦值過程,第16行～第19行是篩選過程,最后一行調用FindCore在導出子圖上進行社區搜索.需要注意的是,最后一行也可以用任意的社區搜索算法進行替換.

因為在權重賦值時把禁止節點權重固定為-1,所以取λ>-1就可以保證篩選出的節點集不包含禁止節點,從而滿足搜索條件,保證了WLP方法的正確性.

算法4.WLP方法.

輸入:G=(V,E),in_set,out_set,k,λ,γ//λ表示權重的閾值,γ表示迭代次數;

輸出:社區C(in_set?C,out_set∩C=?).

例6:圖4和圖5展示了通過WLP方法解決圖3中CCS的過程.在第1輪迭代后,各個點的權重更新為其鄰居點的權重均值,得到了圖4.重復迭代,最后得到圖5.設定閾值為0,可將節點A,A1,A2和A3預先選出;接著,在這4個節點的導出子圖上應用FindCore算法.可以發現,虛線圈出部分已經是一個2-core社區.相比于圖3,它規模更小,結構更緊湊,并且社區內部的成員更靠近節點A,遠離節點B.

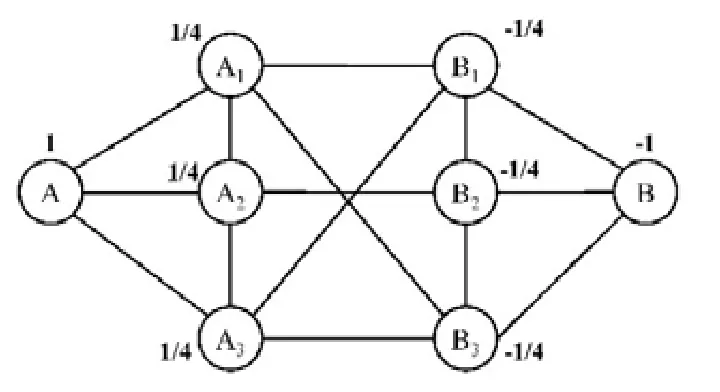
Fig.4 Result of the first propagation圖4 第1輪加權結果

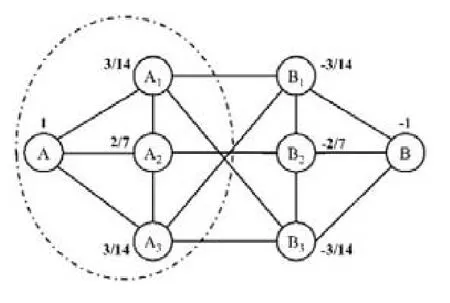
Fig.5 Result of conditional community search (WLP)圖5 通過WLP進行條件社區搜索的結果

3.2.2 WLP方法的復雜度分析

令網絡圖中邊數為m,節點數為n,迭代次數為γ,則通過標簽傳播來給點加權的過程的時間復雜度是O(n)+O(γm),其中,初始賦權重標簽的復雜度O(n).鑒于每一輪迭代的計算過程需要訪問每個節點的所有鄰居,于是,其時間復雜度為O(m).在實際計算中,可以僅維護權重不為 0的節點數組,隨著迭代,再不斷添加而不必將所有點賦予初始值.這樣做可以將上述過程的復雜度降到O(γm).

4 實驗與分析

本節首先介紹實驗環境與數據集,通過實驗展示利用簡化的搜索條件進行條件社區搜索的有效性,最后比較不同條件社區搜索方法的時間開銷和結果社區質量.

4.1 實驗環境與數據集

本文實驗所用機器的CPU是Intel Xeon E5-2650 2.0GHZ,內存大小256GB,操作系統為Windows Server 2008 R2.用Python-3.6.1實現了3種策略下(FF,OTF,SF)的“社區搜索+過濾”方法和WLP方法.

本文實驗采用的真實數據集有Football,DBLP,Amazon和Youtube,其中,Football數據集來自Khorasgani[44],其余數據集來自Stanford Large Network Dataset Collection(http://snap.stanford.edu/data/),具體統計信息見表1,均帶有真實的社區分布.表1最后一列的top5000社區是指數據集提供的前5 000個質量最高的社區(評判標準因數據集而異,如conductance,modularity等,詳見文獻[45]).我們統計發現,DBLP,Amazon和Youtube這3個數據集的top5000社區中都有95%以上的社區規模在50個節點以下.因此在后續實驗中,FindCore算法的搜索上限search_limit設置為50,以便提前終止局部搜索過程,提高算法效率.

Table 1 Datasets表1 數據集

為了研究簡化搜索條件的方法在不同規模網絡圖上的效果,本文還采用人工網絡生成工具 Lancichinetti-Fortunato-Radicchi(LFR)[46]來合成不同規模的網絡圖.具體地,合成網絡圖中節點數量n的變化范圍是 104～105.LFR工具的其他參數設置如下:節點平均度數d為5,節點最大度數dmax為50,最小社區規模cmin為20,最大社區規模cmax為100,拓撲結構混合參數u為0.1.

4.2 社區結果的評價指標

通過參考現有社區發現和社區搜索的評價標準,本文選取F1-measure和Ql(局部模塊度)來評估結果社區的質量,其中,F1-measure衡量了結果社區的正確性,Ql評估了結果社區內部的緊密程度.

F1-measure是準確率和召回率的調和平均值,用于衡量計算得到的結果社區與真實社區的接近程度,其計算公式為

其中,C代表計算出的結果社區,C′是真實社區.F1-measure的值越接近1,則計算結果越精確.需要注意的是,數據集提供的真實社區的獲取方式不盡相同.例如:Football數據集是依據球員的好友關系構建的網絡,同一個俱樂部成員標定為同一社區;DBLP是依據論文作者的協作關系構建的網絡,同一個小組的成員標定為同一社區.

依據數據集給出的真實社區,一種很自然的假定是:當單項條件社區搜索中的必要節點都來自同一真實社區,而禁止節點都在該社區外時,數據集提供的真實社區就是對應單項條件社區搜索的真實社區.在其他情況下,例如必要節點和禁止節點都來自數據集提供的某個真實社區時,本文提出的“社區搜索+過濾”方法以及WLP方法仍有返回結果的可能.該結果往往預示著數據集提供的真實社區中存在著可以細分的子社區結構,但此時的真實社區無法預知.因此,在這種情形下就無法使用F1-measure進行正確性度量,而只關心所得社區的緊密性和社區內成員相對必要節點的遠近,即,從合理性的角度去度量社區結果好壞.

局部模塊度(local modularity)指一個子圖內部所有的邊數與原圖中所有涉及到該子圖中節點的邊數量的比值[47],即:

其中,kin表示社區內部的邊數,kout表示社區內部和外部連接的邊數.Ql越大,表明社區緊密性越好.

除此之外,為了評估社區內節點與必要節點的接近程度,本文設計了相對最短路徑比這一新指標,即社區內節點分別與必要節點和禁止節點的平均最短路徑距離之比(average shortest pathdistance ratio,簡稱ASD-ratio):

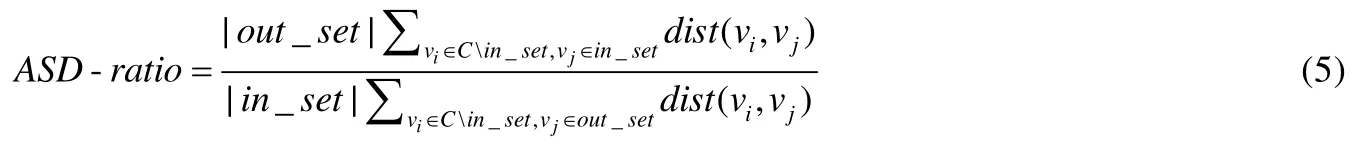
其中,in_set和out_set分別表示必要節點集和禁止節點集,dist(vi,vj)表示vi和vj之間的最短路徑距離,C表示社區結果.ASD-ratio越小,意味著社區內成員與必要節點越近,與禁止節點越遠.

4.3 搜索條件簡化的有效性

第2.3節給出了簡化搜索條件以減少單項條件社區搜索次數的方法.本節將對此進行實驗驗證.

根據第 2節提出的條件社區搜索通用框架,無論搜索條件是否經過簡化,該框架都需要先枚舉所有滿足原始搜索條件的變量組合,簡化搜索條件的有效性在之后的步驟才體現出來.因此在本節實驗中,搜索條件被設計為主析取范式的形式,相當于省去枚舉變量取值過程的開銷.該主析取范式包含q個搜索項,每個搜索項包含相同的v個節點變量.這v個節點變量按照均勻分布從網絡圖中隨機選取.此外,對每個搜索項,按照均勻分布隨機為部分節點變量添加了邏輯非運算符,表示禁止這部分節點出現在社區中.例如,(A∧B∧?C)∨(A∧?B∧C)表示一個包含2個搜索項、3個節點變量A,B和C的主析取范式形式的搜索條件.因為對任意形式的搜索條件總能得出與其等價的主析取范式[40],范式中搜索項的個數和節點變量的個數允許任意指定,并且節點變量是隨機選取的,所以上述搜索條件設計可以表達任意的搜索條件,其完備性得以保證.

本節以OTF方法為例來驗證搜索條件簡化的優勢,其他3種方法的效果類似.公平起見,簡化前后的條件社區搜索方法中的單項條件社區搜索步驟都應用了 FindCore算法.為保證實驗結果的普遍性,在不同的節點變量個數v和不同搜索項個數q下進行了多次對比.對固定的一組v和q,重復10次實驗,取時間開銷的均值.FindCore算法中的k值從2～10的范圍內逐一嘗試,保留使社區規模最大的k值.

圖6展示了簡化前后條件社區搜索方法的時間開銷隨搜索項個數v的變化情況,其中,簡化后條件社區搜索方法的時間開銷包含了化簡過程自身的時間開銷.如圖6(b)～圖6(d)所示:簡化前的條件社區搜索方法的時間開銷基本上和搜索項個數成正比,簡化后的條件社區搜索方法在時間開銷上具有明顯優勢.例如:針對DBLP數據集,當節點個數為5、搜索項個數為14時,簡化前的時間開銷是簡化后時間開銷的5倍以上.這是因為固定節點數量后,搜索項越多,越容易引發搜索項冗余現象,也越容易出現公共搜索變量.于是,當冗余的搜索項數量增多時,簡化后的條件社區搜索方法的提高效果更為明顯.

圖7展示了簡化前后條件社區搜索方法的時間開銷隨節點變量個數q的變化情況,其中,簡化后條件社區搜索方法的時間開銷包含了化簡過程自身的時間開銷.如圖7(b)～圖7(d)所示:從時間開銷隨節點個數的變化趨勢上看,節點個數增加并不會影響簡化后的條件社區搜索方法的優勢.例如在圖7(b)中,節點個數從4增加到6,簡化后時間開銷穩定地為簡化前時間開銷的1/4.

需要注意的是,圖6(a)和圖7(a)中存在簡化后條件社區搜索方法的時間開銷更高的情形(不過整體時間開銷均在0.3s內).這是因為:一方面,圖6(a)和圖7(a)對應的Football數據集規模較小,于是運行社區搜索算法的開銷較小;另一方面,社區搜索條件的化簡過程也需要一定開銷,條件越復雜,則化簡過程自身需要越多的時間.因此,當條件較復雜(比如搜索項數量大于 8)時,化簡過程的時間開銷占到較大比重,從而使簡化后的社區搜索方法耗時更多.

Fig.6 Time costs of conditional community search with different query numbers (# node variablev=5)圖6 不同搜索項個數下條件社區搜索方法的時間開銷(節點變量個數v=5)

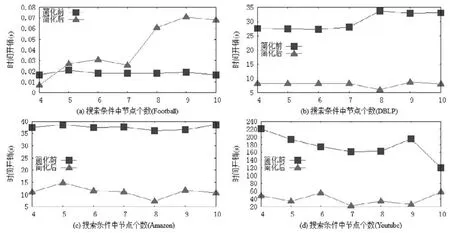
Fig.7 Time costs of conditional community search with different node numbers (# queriesq=10)圖7 不同節點個數下條件社區搜索方法的時間開銷(簡化前搜索項個數q=10)

為了分析最簡與或式化簡程度與條件社區搜索方法的關系,給出冗余項數目的概念并展示冗余項數目對簡化后條件社區搜索方法時間開銷的影響.具體地,冗余項數目定義為化簡為最簡與或式前后減少的搜索項個數.圖8展示了DBLP等3個數據集簡化后條件社區搜索方法的時間開銷隨冗余項數目的變化情況,其中,節點變量個數v為8,簡化前搜索項個數q為8.顯然,隨冗余項數目的增加,時間開銷進一步得到縮減.需要說明的是,因為Football數據集上的整體時間開銷較小,所以沒有進行展示.

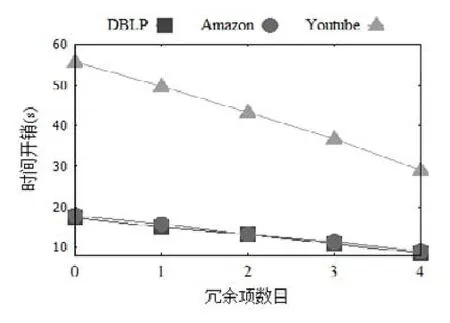
Fig.8 Effect of redundant items on the time cost圖8 冗余項數目對時間開銷的影響

圖9對比了不同網絡圖規模下條件社區搜索方法的時間開銷,其中,網絡圖的規模由圖中的節點數量表示.對不同節點變量個數v和搜索項個數q,簡化前后條件社區搜索方法的時間開銷都隨網絡圖規模的增大而增加,并且簡化后的條件社區搜索方法一直保持明顯優勢.實際上,社區規模大小只影響每次單項條件社區搜索的時間開銷而不影響對搜索條件的化簡過程,因此,化簡過程在大規模網絡圖上依然適用.

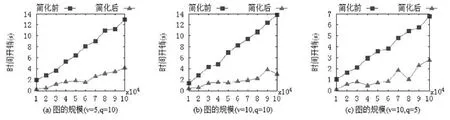
Fig.9 Time costs of conditional community search with different graph size圖9 不同網絡圖規模下條件社區搜索的時間開銷

4.4 單項條件社區搜索方法的對比實驗

第 3節提出了單項條件社區搜索方法,即“社區搜索+過濾”的方法(使用 3種不同策略的方法分別記為FF,OTF和 SF)和基于標簽傳播給點加權的方法(記為 WLP).本節將從時間開銷和社區結果質量角度對上述方法進行實驗.

由定義4可知,單項條件社區搜索的輸入條件只有一種可滿足的取值組合,因此可以通過隨機指定必要節點和禁止節點的個數來構造搜索條件.鑒于用戶輸入的節點總數通常較小,實驗中設計了 5種類型的單項社區搜索條件(見表2),對應不同的必要節點和禁止節點個數.例如,編號i對應形如A∧B∧?C的搜索條件,包含2個必要節點和 1個禁止節點.在執行具體搜索實驗時,節點變量替換為具體的節點編號,且每一種搜索條件對應100組不同的具體節點編號.不同方法中,每類搜索條件的時間開銷、F1-measure、Ql以及ASD-ratio都是相關的100組實驗的均值.

為公平起見,所有社區搜索算法均采用FindCore算法.對不同節點變量,k值在2～10的范圍內嘗試,留下使社區規模最大的一個.

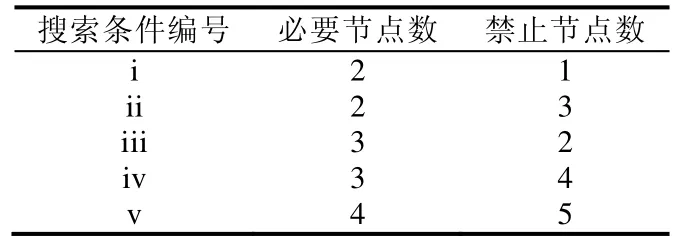
Table 2 Design of search conditions表2 搜索條件設計

圖10展示了當搜索條件為iii,WLP方法中的閾值λ在[0,0.4]范圍內取值時所得社區F1-measure的變化情況.當λ超過0.2時,在DBLP上難以找到合適社區,而在Football上社區準確性下降.需要說明的是,在兩個數據集上,-1<λ<0時F1-measure的值與λ=0時F1-measure的值相等;當λ>0.4時,得到的F1-measure的值均為0,所以在圖中沒有顯示上述范圍內的變化情況.考慮到取較大閾值可減小社區搜索范圍,因此在后續實驗中,統一將閾值λ設置為0.2.

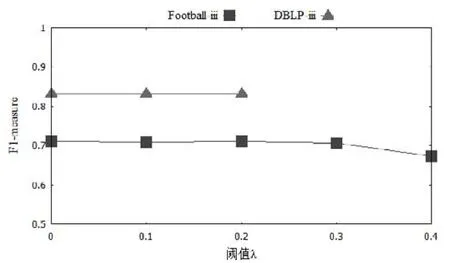
Fig.10 F1-measure with different thresholds of WLP method圖10 不同閾值下WLP方法得到的F1-measure

根據第3.2.1節中WLP方法的具體過程,第γ輪迭代中相對于必要節點和禁止節點的傾向性會傳遞給必要節點和禁止節點的γ跳鄰居.此外,考慮到六度分離的原則,當迭代至 6次時,網絡中的大部分節點已經得到了能反映出傾向性的權重.因此,實驗中的迭代次數γ被設置為6.

圖11對比了4種不同方法的時間開銷.圖11(a)和圖11(b)分別是在Football和DBLP數據集上取得的實驗結果,橫坐標編號對應搜索條件.

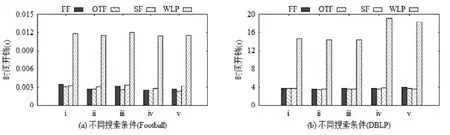
Fig.11 Time costsof different singleconditionalcommunity search methods圖11 不同單項條件社區搜索方法的時間開銷對比

因為WLP方法需要進行節點權重的計算,且該計算涉及圖中所有邊,較為費時,所以其時間開銷最大.“社區搜索+過濾”方法的3種策略FF,OTF和SF的時間開銷相近,其中,OTF策略相對稍好.這是因為FF策略存在部分冗余刪除,SF策略需要進一步調整社區結構,而 OTF策略在搜索過程中過濾掉禁止節點,從而避免了另兩種策略在效率上的不足.

圖12展示了4種不同方法在Football和DBLP數據集上所得社區結果的F1-measure.在每次單項條件社區搜索的具體實驗中,要求其搜索條件中的必要節點來自同一實際社區,同時禁止節點來自該社區外.這樣就可以根據數據集附帶的真實社區結果計算F1-measure.從圖12(a)和圖12(b)可以看出:無論是Football還是DBLP數據集,3種不同策略下“社區搜索+過濾”方法得到的F1-measure都基本相同.這表明給定符合真實社區分布的搜索條件,這3種策略都能找到相同準確程度的社區結果.WLP方法得到的社區搜索結果在多數搜索條件下有更好的準確性,在少數條件下準確性不如其他方法,如圖12(a)的 ii和圖12(b)的 i,iii和iv,但是相對差異并不明顯.這是由于WLP方法的結果受到禁止節點的影響,從而產生波動.例如:當禁止節點離真實社區較近時,WLP方法一般會得到比真實社區更小的社區.這是因為在真實社區內部,有部分與禁止節點相連的節點會被閾值過濾排除在外.這實際上是為使社區內成員與必要節點更接近而付出的必要開銷.

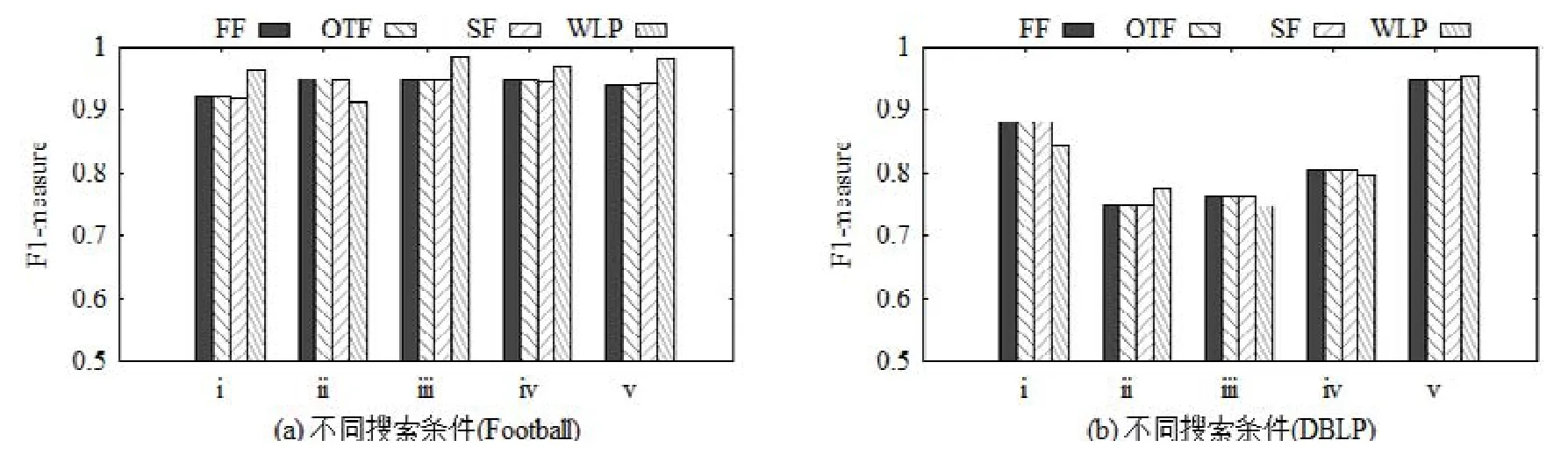
Fig.12 F1-measure of different singleconditional community search methods圖12 不同單項條件社區搜索方法的F1-measure對比

圖13對比了通過不同方法所得結果社區的局部模塊度Ql,其中,圖13(b)的搜索條件中,禁止節點和必要節點來自同一社區,即搜索條件和數據集提供的真實結果有沖突,而圖13(a)則不存在這樣的沖突.在有沖突的情形下,容易發現:在“社區搜索+過濾”方法的3種不同策略中,SF所得結果對應的Ql較低,而FF和OTF的Ql相對較高.這是因為圖中顯示的Ql為多次實驗的均值,在搜索條件存在沖突的情形下,SF在調整社區結構時可能無法得到社區結果,此時的Ql被記為0,從而導致SF的平均Ql降低.在搜索條件不存在沖突時,這3種策略所得社區結果具有相同緊密程度.通過 WLP方法得到的社區,在緊密程度上由于受禁止節點的影響存在較大波動.此外,圖12和圖13的結果也能驗證定理2,即,應用FF策略和OTF策略的FindCore算法得到的結果是相同的.

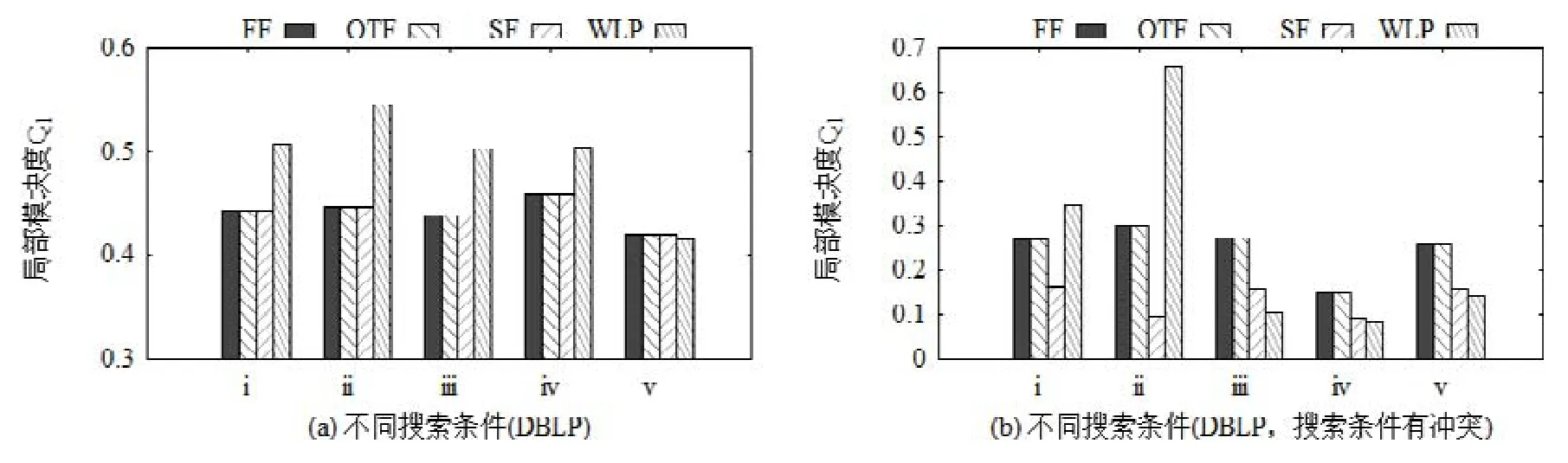
Fig.13 Qlof singleconditional community search methods圖13 不同單項條件社區搜索方法的Ql對比

圖14展示了不同方法所得結果社區的ASD-ratio.顯然,WLP方法在兩個數據集和不同的搜索條件下都具有最小的 ASD-ratio.這表明 WLP方法能夠充分考慮必要節點和禁止節點的影響,得到社區成員與必要節點更接近的社區.

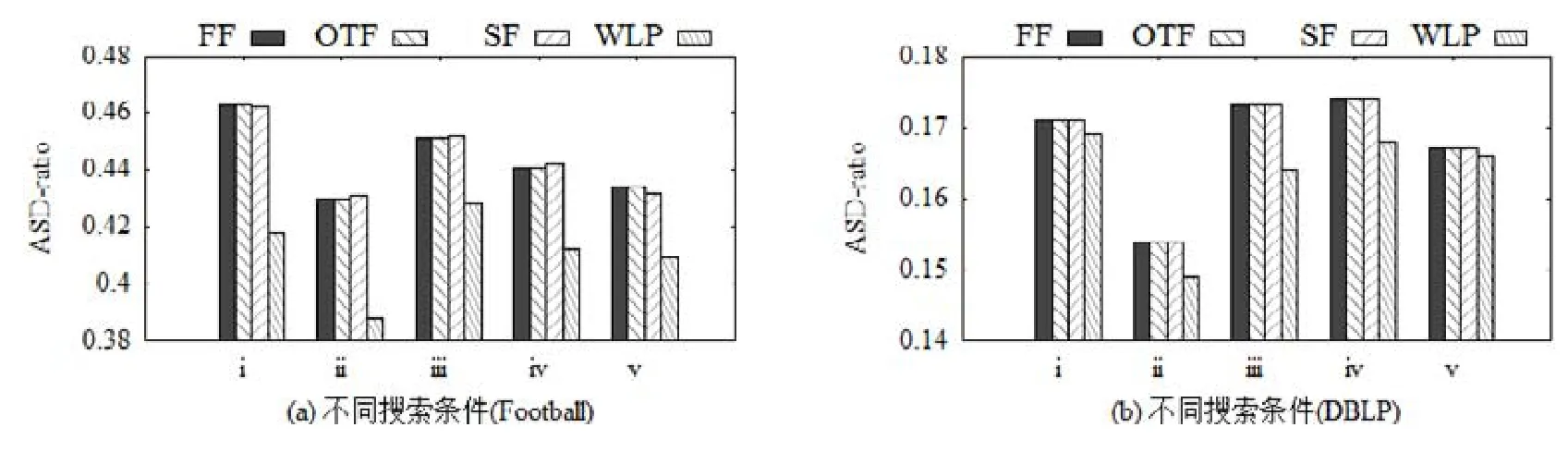
Fig.14 ASD-ratio of different singleconditional community search methods圖14 不同單項條件社區搜索方法的ASD-ratio對比

上述實驗結果表明:采用FF和OTF策略的“社區搜索+過濾”方法可以有效處理CCS,使用OTF策略則可略微提升效率.WLP方法盡管需要更多的時間開銷,所得社區在準確性和緊密程度上存在波動,但是其結果能夠體現出社區內成員對于必要節點的傾向性,排除與禁止節點相近的節點,使社區內成員與必要節點更接近,且在ASD-ratio上最優,具有較高的應用價值.

5 結束語

條件社區搜索問題是在傳統的社區搜索問題基礎上,結合實際需求提出的新問題,它包含了現有社區搜索問題,并且考慮了特定節點能否存在于社區中等復雜條件約束.

本文給出了 CCS的形式化定義,并使用布爾表達式表示搜索條件.在此基礎上,本文提出了解決 CCS的通用框架,將CCS分解為多個SCCS來處理,并通過簡化搜索條件對通用框架進行了優化.對于SCCS,本文提出了“社區搜索+過濾”的方法(包括FF,OTF和SF這3種策略)和基于標簽傳播給點加權的WLP方法.通過在4個真實數據集上的大量實驗,比較了這些方法的時間開銷和社區結果.實驗結果表明,使用OTF策略的“社區搜索+過濾”方法在時間開銷和社區結果上具有優勢.如果考慮用戶在使用條件社區搜索時讓社區成員遠離禁止節點的需求,那么 WLP方法能夠充分考慮必要節點和禁止節點的影響,找到社區內成員與必要節點更接近的社區結果.

條件社區搜索的研究尚處在探索階段,后續會考慮向CCS中引入更多類型的社區定義.對于SCCS,希望找到一種新的社區搜索算法,使得社區結構在準確性和緊密程度上達到最優的同時也能考慮必要節點和禁止節點的影響.