劣質數據上代價敏感決策樹的建立?
齊志鑫,王宏志,周 雄,李建中,高 宏
(哈爾濱工業大學 計算機科學與技術學院,黑龍江 哈爾濱 150001)
分類是數據挖掘和機器學習領域中常見的一類任務,該任務從訓練數據中提取模型,再利用該模型預測未知的數據類別[1].目前,有很多用于完成分類任務的方法被提出,如決策樹[2]、貝葉斯網[3]、神經網絡[4]、基于實例的推理[5]等.在這些方法中,決策樹憑借易解釋、計算效率高、能夠生成易理解的分類規則等優勢得到了眾多關注,并被廣泛應用于分類任務中[6].
起初,大量決策樹研究著眼于最大化分類準確率或最小化分類誤差[7-9].然而,由于一個分類任務可能產生多種類型的代價,越來越多的研究工作關注于代價敏感決策樹的建立[10-12].在目前研究的代價類型中,兩種最常見的代價是誤分類代價和測試代價[13].誤分類代價是指一個屬于類j的實例被誤分類為類i的代價,而誤分類所產生的代價常常是不均衡的.例如,將一個病人診斷為健康的代價往往比將一個健康的人診斷為病人的代價大很多.除了誤分類代價,每一次測試也關聯著相應的代價.例如在醫療診斷中,每一次血常規檢測都存在一個相關聯的代價[1].
現如今,隨著數據量急劇增長,劣質數據的出現也愈發頻繁[14].在建立代價敏感決策樹時,訓練數據集中的劣質數據會對分裂屬性的選擇和決策樹結點的劃分造成一定的影響.因此在進行分類任務前,需要提前對數據進行劣質數據清洗.然而在實際應用中,由于數據清洗工作所需要的時間和金錢代價往往很高,許多用戶給出了自己可接受的數據清洗代價最大值,并要求將數據清洗的代價控制在這一閾值內[15].因此,除了誤分類代價和測試代價以外,劣質數據的清洗代價也是代價敏感決策樹建立過程中的一個重要因素.然而,現有代價敏感決策樹建立的相關研究沒有考慮數據質量問題.為了彌補這一空缺,本文將劣質數據的清洗代價納入代價敏感決策樹建立問題的考慮因素中,該問題帶來了以下挑戰.
(1) 由于清洗后的數據將用于建立代價敏感決策樹,第 1個挑戰是如何將代價敏感決策樹的建立目標融合到數據清洗方法中;
(2) 由于不同用戶設定的數據清洗代價閾值不同,不同數據集中劣質數據所占比率不同,第 2個挑戰是針對不同的情況,如何選擇最優的代價敏感決策樹建立方法.
鑒于這兩點挑戰,本文從問題定義入手,將用戶設定的數據清洗代價閾值納入到代價敏感決策樹建立的問題中.然后,針對這一問題給出融合數據清洗算法的代價敏感決策樹建立方法.最后,測試改變用戶設定的數據清洗代價閾值或改變數據集中劣質數據比率時不同方法的總代價、分類準確率和效率,從而得出不同情況下最優的代價敏感決策樹建立方法.本文的主要貢獻有以下幾點.
(1) 研究了劣質數據上代價敏感決策樹的建立問題,是目前首個考慮到代價敏感決策樹建立過程中的數據質量問題的工作;
(2) 針對劣質數據上的代價敏感決策樹建立問題,本文提出了 3種融合數據清洗算法的代價敏感決策樹建立方法,即融合基于分裂屬性收益的分步清洗算法的代價敏感決策樹建立方法、融合基于分裂屬性收益和清洗代價的一次性清洗算法的代價敏感決策樹建立方法、融合基于分裂屬性收益和清洗代價的分步清洗算法的代價敏感決策樹建立方法;
(3) 本文通過大量實驗驗證了所提出的3種代價敏感決策樹建立方法的總代價、分類準確率和分類效率,并給出了不同情況下最優的代價敏感決策樹建立方法.
本文第 1節對代價敏感決策樹建立問題相關的研究工作進行總結.第 2節對本文問題相關的定義進行介紹.第3節對本文提出的3種融合數據清洗算法的代價敏感決策樹建立方法進行詳細地闡述.第4節對本文的實驗評估過程和實驗結果進行討論和分析,并給出實驗結論.第 5節總結全文,并對未來值得關注的研究方向進行初步探討.
1 相關工作
目前,代價敏感決策樹建立問題的研究目標主要包括3種:第1種是最小化決策樹的誤分類代價;第2種是最小化決策樹的測試代價;第 3種是最小化決策樹的誤分類代價和測試代價總和[13].本文選擇的研究目標是第3種.
針對不同的問題目標,許多代價敏感決策樹建立方法被提出.這些方法可以分為兩大類.
· 第1類是采用貪心的方法來建立一棵單獨的決策樹,例如:CS-ID3算法[16]采用基于熵的選擇方法在決策樹建立過程中最小化代價,AUCSplit算法[17]在決策樹建立之后最小化代價;
· 第2類是非貪心的方法,該方法生成多個決策樹,例如遺傳算法ICET[18]、將現有基于準確率的方法包裝在一起的MetaCost算法[19].
按照時間順序來看,Hunt等人首先發現了誤分類和測試對人們的決策存在一定的影響,并提出了概念學習系統框架[20].隨后,ID3算法[21]采用了概念學習系統框架的部分思想,并使用了信息論評估參數來選擇特征.在信息論方法被提出后,許多在決策樹建立過程中最小化代價的方法被陸續提出,如CS-ID3算法[16]、EG2算法[22].然后,在決策樹建立后最小化代價的方法被提出,如 AUCSplit算法[17].之后,遺傳方法如 ICET算法[18]、提升法如UBoost算法[23]、裝袋法如MetaCost算法[19]等被提出.隨后,多重結構的方法如LazyTree算法[24]、隨機方法如ACT算法[25]、TATA算法[26]被陸續提出.
在最小化代價敏感決策樹的誤分類代價和測試代價的基礎上,有研究著眼于包含其他限制因素的代價敏感決策樹建立問題.例如:由于有些分類任務需要在規定的時間內完成,在時間限制下的代價敏感決策樹建立方法被提出[1].有時用戶會對分類任務的準確率提出預期的要求,因此面向用戶需求的代價敏感決策樹建立方法被提出[27].然而,目前并未有研究關注劣質數據上的代價敏感決策樹建立.因此,本文將彌補這一空缺.
2 問題定義
本節將對劣質數據上代價敏感決策樹建立問題的相關定義進行介紹.
2.1 決策樹
決策樹T具有樹結構,是有向無環圖的一個特例.決策樹中包含根結點、內部結點和葉子結點的有限集合、連接兩個結點的邊的集合.圖1是決策樹的實例.
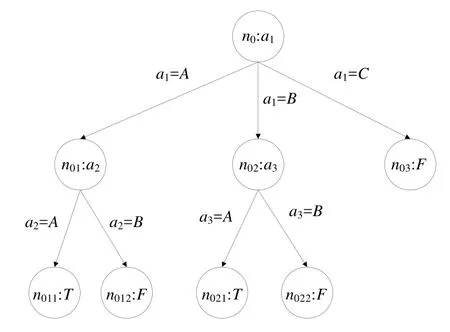
Fig.1 An instance of decision tree圖1 決策樹實例
如圖1所示,ni表示第i個結點.如果ni是內部結點,那么該結點會關聯著屬性a(ni),a(ni)被稱為在結點ni中被用到的測試屬性.如果ni是葉子結點,那么該結點關聯著一個類別標簽值.本文用inter(T)表示T中所有內部結點的集合,用leaf(T)表示T中所有葉子結點的集合,Ti表示T中根為ni的子樹.
本文用有序對(ni,nj)表示決策樹中一條關聯著結點ni和nj的邊,其中,ni是nj的父結點.當ni是關聯測試屬性a(ni)的內部結點時,邊(ni,nj)關聯一個單獨的值或一個值集合,這些值都是a(ni)可能的屬性值.決策樹中的一條路徑是邊的一個序列,本文用path(ni,nj)表示從ni到nj的路徑.假設ni到nj之間的序列是n1,n2,…,nm,那么path(ni,nj)={(ni,n1),(n1,n2),…,(nm,nj)},本文用n(ni,nj)={n1,n2,n3,…,nm}表示從ni到nj的路徑上所有中間結點的集合.
決策樹分類器通過在訓練數據集D上學習構建而成,dk表示D中的第k條記錄.每條記錄由屬性值集合和類別標簽構成.本文用a表示屬性值集合,ax表示a中的第x個屬性.表1是訓練數據集的一個實例,每一條記錄由ID、5個屬性和1個類別標簽組成.
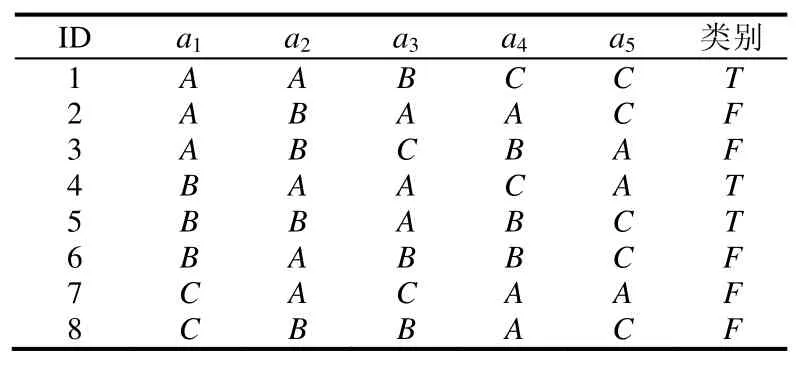
Table 1 An instance of training dataset表1 訓練數據集實例
本文用D(ni)表示D中屬性值遵循path(root,ni)中邊上屬性值的記錄集合,這說明D(ni)是滿足path(root,ni)上所有測試的記錄集合.D(root)表示整個訓練數據集D,|D(ni)|表示D(ni)中的記錄個數.根據表1中的訓練數據集構建的決策樹如圖2所示.
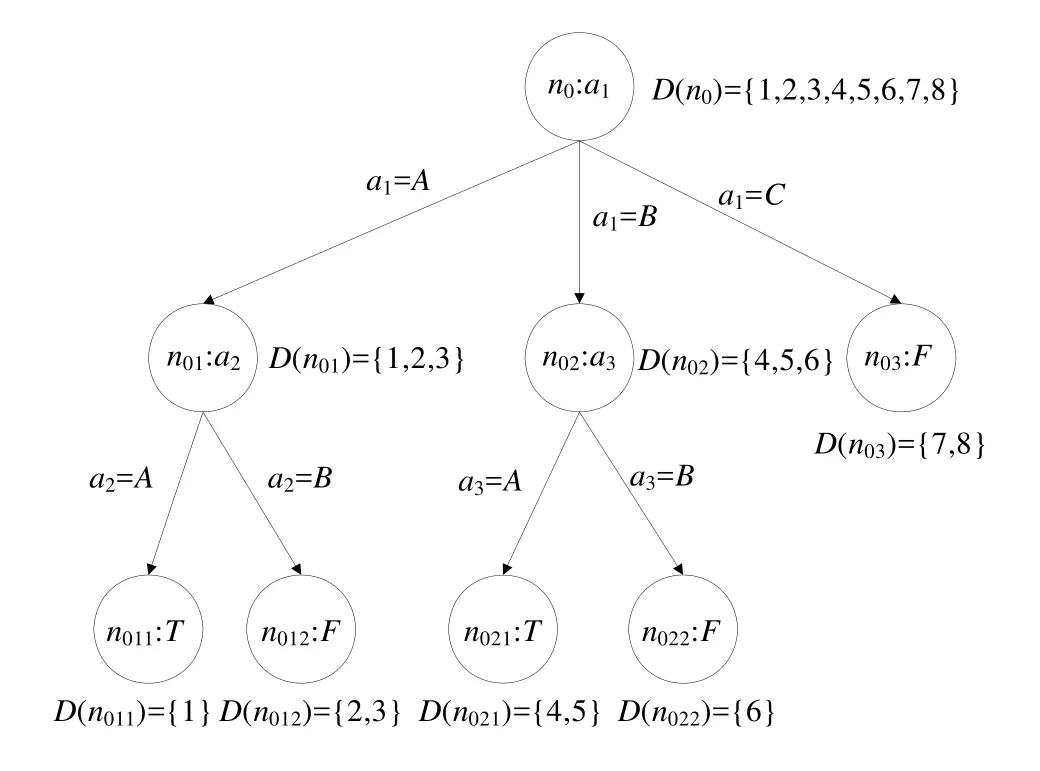
Fig.2 Decision tree trained by Table 1圖2 根據表1訓練成的決策樹
2.2 誤分類代價和測試代價
誤分類代價是指一個屬于類j的實例被誤分類為類i的代價.假設訓練數據集中有m個類別,那么誤分類代價矩陣可以用m×m的矩陣表示,見表2.本文用ClassCost(i,j)表示當一個實例屬于類j時,將其誤分類為類i的代價.從表2可知,ClassCost(T,T)=0,ClassCost(T,F)=10,ClassCost(F,T)=20,ClassCost(F,F)=0.

Table 2 A matrix of misclassification costs表2 誤分類代價矩陣
當為葉子結點分配一個標簽時,可能會導致該葉子結點關聯的記錄產生一定的誤分類代價.因此,本文用ClassCost(ni,lj)表示給結點ni分配標簽為lj的葉子結點時產生的誤分類代價,即:

例如,對于表1中的訓練數據,ClassCost(root,T)=0+10+10+0+0+10+10+10=50,ClassCost(root,F)=20+0+0+20+20+0+0+0=60.
本文用TestCost(ax)表示對屬性ax進行測試所需要的代價,用ArrCost(ni,T)表示一條記錄從T的根結點到達ni所需的總測試代價,即.表1中屬性的測試代價見表3.從表3可知,ArrCost(n01,T)=4,ArrCost(n011,T)=4+6=10.

Table 3 TestCost of attributes表3 屬性的測試代價
每一條記錄都會經過從決策樹根結點到葉子結點的測試,因此,結點ni中的記錄到達ni所花費的總測試代價為ArrCost(ni,T)×|D(ni)|.此外,ni獲得一個類別標簽時會產生一定的誤分類代價.本文用NodeCost(ni)表示誤分類代價和測試代價的總代價.如果將結點ni作為一個葉子結點,則
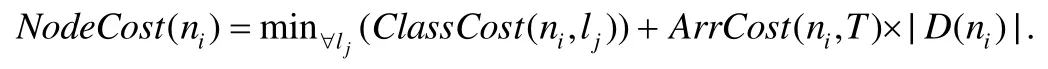
例如,對于圖2中的決策樹,NodeCost(root)=50+0×8=50,NodeCost(n01)=20+4×3=32.
圖2中其余結點的NodeCost值見表4.

Table 4 NodeCost of nodes表4 結點的NodeCost值
本文用TreeCost(T)表示決策樹T的總代價,即.例如,圖2中決策樹的總代價為TreeCost(T)=NodeCost(n011+n012+n021+n022+n03)=10+20+14+7+8=59.
2.3 檢測代價和修復代價
劣質數據清洗工作往往由錯誤檢測和修復兩部分組成[28].在對訓練數據集進行清洗的過程中,首先需要對數據集中的劣質數據進行檢測,然后針對檢測到的劣質數據進行相應的修復.數據集中的每一個屬性都對應著檢測該屬性值中可能存在的錯誤所需要花費的代價和修復該屬性錯誤值所需要花費的代價.
本文用DetCost(ax)表示對屬性ax中的每個值進行錯誤檢測所需要花費的代價.因此,對屬性ax中全部屬性值進行劣質數據檢測所需要的代價是DetCost(ax)×|ax|.如果檢測到屬性ax中的劣質數據個數為|Er(ax)|,那么對屬性ax中的全部劣質數據值進行修復所需要的代價是Rep(ax)×|Er(ax)|,其中,Rep(ax)是修復屬性ax中的每個劣質數據值所需要的代價.在本文中,xd表示屬性ax中完成了劣質數據檢測的屬性值個數,xr表示屬性ax中完成了劣質數據修復的屬性值個數.然而在實際應用中,由于數據清洗工作所需要的時間和金錢代價往往很高,許多用戶給出了自己可接受的數據清洗代價最大值.因此,本文用MaxCost表示用戶可接受的數據清洗代價閾值,并將數據清洗的代價控制在這一閾值內.
2.4 劣質數據上代價敏感決策樹建立問題
給定一個訓練數據集、用戶設定的數據清洗代價最大值、誤分類代價矩陣、每個屬性對應的測試代價、檢測代價和修復代價,劣質數據上代價敏感決策樹建立問題定義如下:基于訓練數據集,建立一個代價敏感決策樹,使得該決策樹的誤分類代價和測試代價總和最小,且清洗該數據集的檢測代價和修復代價總和不超過用戶設定的數據清洗閾值.
該問題的形式化描述是已知訓練數據集D,數據清洗代價最大值MaxCost,誤分類代價ClassCost(ni,lj),測試代價TestCost(ax),檢測代價DetCost(ax)和修復代價,建立T,使得:
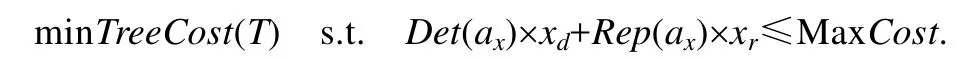
其中,
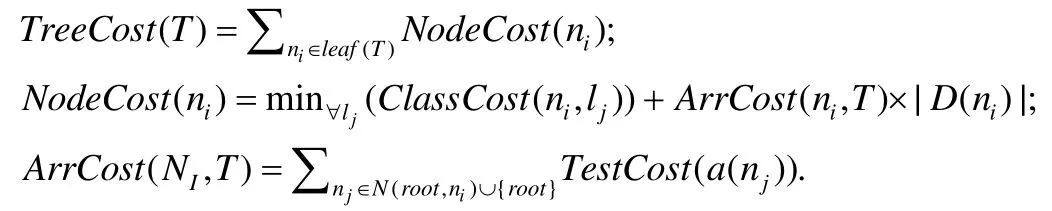
3 融合數據清洗算法的代價敏感決策樹建立方法
為了解決劣質數據上代價敏感決策樹的建立問題,本文提出了 3種融合數據清洗算法的代價敏感決策樹建立方法,即融合基于分裂屬性收益的分步清洗算法的代價敏感決策樹建立方法、融合基于分裂屬性收益和清洗代價的一次性清洗算法的代價敏感決策樹建立方法和融合基于分裂屬性收益和清洗代價的分步清洗算法的代價敏感決策樹建立方法.本節將分別對這 3種代價敏感決策樹建立方法進行闡述,并對各個方法的適用情況進行討論.
3.1 融合基于分裂屬性收益的分步清洗算法的代價敏感決策樹建立方法
由于代價敏感決策樹的建立目標是最小化誤分類代價和測試代價的總和,因此可以將誤分類代價和測試代價總和的減少程度作為決策樹分裂屬性選取的標準.本文定義了分裂屬性收益的概念來表示誤分類代價和測試代價總和的減少程度.
本文用Benefit(ax,ni)表示用屬性ax分裂結點ni的收益,結點ni會被分裂為若干個孩子結點.分裂屬性收益Benefit(ax,ni)定義為
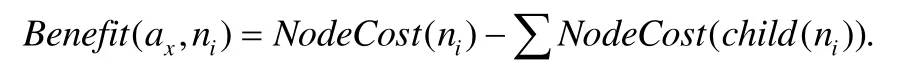
例如在圖2中,NodeCost(n01)=32,NodeCost(n011)=10,NodeCost(n012)=20.因此,Benefit(a2,n01)=32-(10+20)=2.
融合基于分裂屬性收益的分步清洗算法的代價敏感決策樹建立方法的過程如下:在決策樹建立的每一步中,選擇收益最大的分裂屬性;先對該分裂屬性中的值進行劣質數據檢測和修復,再將該屬性用于決策樹的分裂過程中;當所花費的清洗代價達到用戶設定的最大值后,不再對后續的分裂屬性進行清洗,直接用于決策樹的分裂過程中;當結點中所有記錄所對應的類別標簽相同,或沒有分裂屬性的收益為正值時不再對該結點進行分裂,將其標記為葉子結點,其類別標簽為使得誤分類代價最小的類別.
上述過程中,基于分裂屬性收益的分步清洗算法見算法1.算法的輸入是待清洗的訓練數據集、用戶給定的清洗代價閾值、數據集中每個屬性對應的劣質數據檢測代價和修復代價.首先,對根結點的分裂屬性收益進行計算,選取收益最大的屬性作為分裂屬性(第1行~第5行).對該屬性中的屬性值進行劣質數據檢測和修復,并計算剩余的清洗代價是否足夠對訓練數據集中該屬性的全部屬性值進行檢測:如果足夠,那么對該屬性的所有屬性值進行劣質數據檢測(第 6行~第 9行);如果不足夠,那么對該屬性部分屬性值進行檢測(第 10行~第 14行).在檢測出分裂屬性中包含的劣質數據后,對劣質數據進行修復,并計算剩余的清洗代價是否足夠對全部劣質數據進行修復:如果足夠,那么對該屬性中包含的所有劣質數據進行修復(第15行~第17行);如果不足夠,那么對部分劣質數據進行修復(第18行~第21行).然后,繼續為下一個結點尋找分裂屬性并清洗(第22行).當清洗代價達到用戶給定的閾值或決策樹中全部結點都被清洗完畢后,返回清洗后的訓練數據集(第23行).
算法1.基于分裂屬性收益的分步清洗算法.
輸入:訓練數據集Dm×n,清洗代價閾值 MaxCost,每個屬性x∈{1,2,…,n}的劣質數據檢測代價Det(ax)和修復代價Rep(ax);
輸出:清洗后的訓練數據集Dm×n.


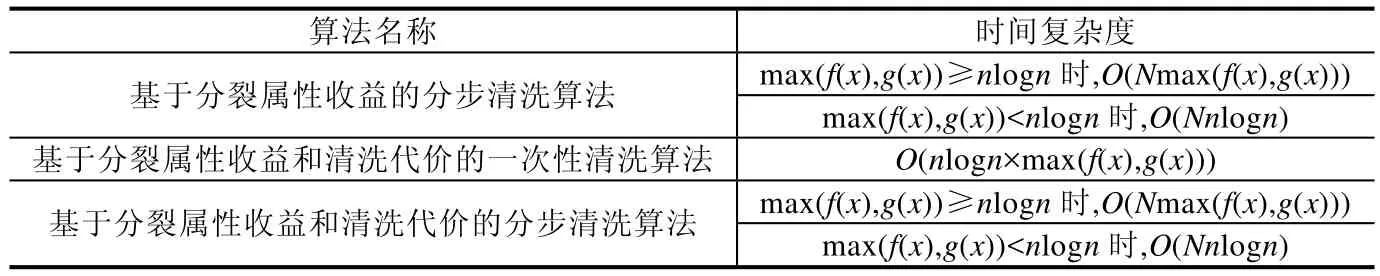
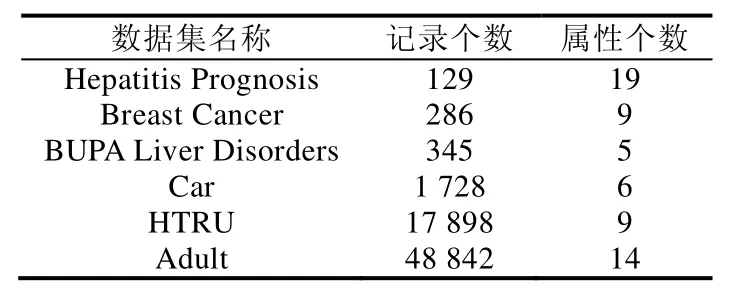
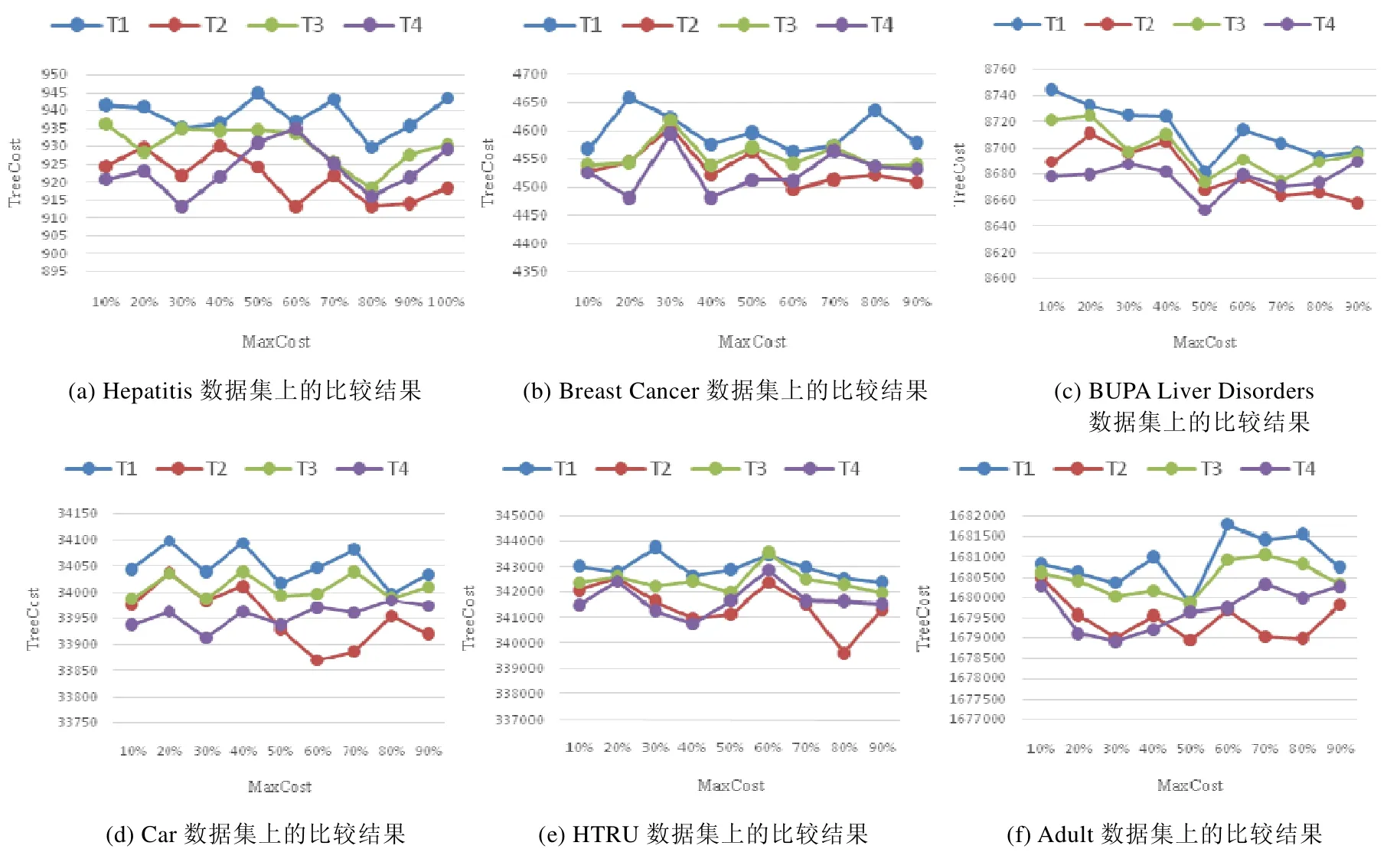
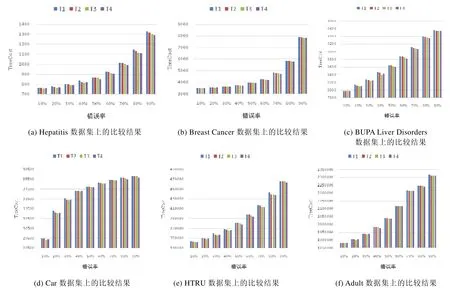
算法1的時間復雜度取決于決策樹中的結點個數N、訓練數據集中的屬性個數n和記錄個數m.假設劣質數據檢測函數Detect(x)的時間復雜度為O(f(x)),劣質數據修復函數Repair(x)的時間復雜度為O(g(x)),當max(f(x),g(x))≥nlogn時,算法1的時間復雜度是O(Nmax(f(x),g(x)));當max(f(x),g(x)) 融合基于分裂屬性收益的分步清洗算法的代價敏感決策樹建立方法盡可能地將代價敏感決策樹中前幾層的分裂屬性進行清洗后再用于分裂過程.由于決策樹中層次低的分裂結點重要性高于層數高的分裂結點,所以該方法保證了決策樹結點分裂的有效性,有效降低了決策樹的誤分類代價和測試代價總和,使得決策樹在后續的分類任務中受訓練數據集中的劣質數據影響較小.然而,當用戶設定的清洗代價閾值較小時,該方法可能會對清洗代價高的屬性優先進行清洗,使得能夠被清洗到的屬性個數較少,從而導致在這種情況下,該方法對劣質數據的清洗效果不大. 為了解決融合基于分裂屬性收益的分步清洗算法的代價敏感決策樹建立方法所存在的問題,本文將數據清洗代價考慮到數據清洗算法中,希望選擇收益高且清洗代價低的屬性優先進行清洗.本文定義了收益與清洗代價比來平衡分裂屬性收益和清洗代價這兩個沖突的因素,即Benefit(ax,n0)/(Det(ax)+Rep(ax)),其中,Benefit(ax,n0)是屬性ax在決策樹根結點n0時的分裂屬性收益,Det(ax)和Rep(ax)分別是對屬性ax的每個屬性值進行劣質數據檢測和修復的代價. 融合基于分裂屬性收益和清洗代價的一次性清洗算法的代價敏感決策樹建立方法的過程如下:將訓練數據集中的各個屬性按照收益與清洗代價比進行排序,按照順序進行一次性數據清洗.在每一次選擇分裂屬性時,對每個屬性重新計算分裂屬性收益Benefit(ax,n0),選擇收益最大的屬性作為分裂屬性.當結點中所有記錄所對應的類別標簽相同,或沒有分裂屬性的收益為正值時停止對該結點的分裂,將其標記為葉子結點,其類別標簽為使得誤分類代價最小的類別. 上述過程中基于分裂屬性收益和清洗代價的一次性清洗算法見算法 2.算法的輸入是待清洗的訓練數據集、用戶給定的清洗代價閾值、數據集中每個屬性對應的劣質數據檢測代價和修復代價.首先,對每個屬性在根結點的收益與清洗代價比從大到小排序(第1行~第4行).按照順序選取屬性進行劣質數據檢測和修復(第5行、第6行).計算剩余的清洗代價是否足夠對訓練數據集中該屬性的全部屬性值進行檢測:如果足夠,那么對該屬性的所有屬性值進行劣質數據檢測(第7行~第10行);如果不足夠,那么對該屬性部分屬性值進行檢測(第11行~第15行).在檢測出分裂屬性中包含的劣質數據后,對劣質數據進行修復,并計算剩余的清洗代價是否足夠對全部劣質數據進行修復:如果足夠,那么對該屬性中包含的所有劣質數據進行修復(第16行~第18行);如果不足夠,那么對部分劣質數據進行修復(第19行~第22行).然后,按照順序對下一個屬性進行清洗(第23行).當清洗代價達到用戶給定的閾值或全部屬性都被清洗完畢后,返回清洗后的訓練數據集(第24行). 算法2.基于分裂屬性收益和清洗代價的一次性清洗算法. 輸入:訓練數據集Dm×n,清洗代價閾值MaxCost,每個屬性x∈{1,2,…,n}的劣質數據檢測代價Det(ax)和修復代價Rep(ax); 輸出:清洗后的訓練數據集Dm×n. 算法 2的時間復雜度取決于訓練數據集中的屬性個數n和記錄個數m.假設劣質數據檢測函數Detect(x)的時間復雜度為O(f(x)),劣質數據修復函數Repair(x)的時間復雜度為O(g(x)),算法 2的時間復雜度是O(nlogn×max(f(x),g(x))). 融合基于分裂屬性收益和清洗代價的一次性清洗算法的代價敏感決策樹建立方法盡可能地優先清洗收益大且清洗代價小的屬性.該方法提前將數據集中的劣質數據清洗完畢,使得在決策樹建立過程中能夠直接利用清洗后的屬性收益選取分裂屬性,很大程度上降低了劣質數據對決策樹的影響.此外,該方法采用一次性清洗策略,與分步清洗策略相比節約了時間.然而,該方法一次性清洗到的屬性不一定都會在后續的決策樹建立過程中被選作分裂屬性.因此,在劣質數據比例較大的情況下,該方法可能沒有清洗到決策樹建立過程中的某些分裂屬性,導致數據清洗過程對分類任務的作用不大. 為了解決融合基于分裂屬性收益和清洗代價的一次性清洗算法的代價敏感決策樹建立方法所存在的問題,本文提出了融合基于分裂屬性收益和清洗代價的分步清洗算法的代價敏感決策樹建立方法.該方法的過程如下:在決策樹建立的每一步中,選擇收益與清洗比最大的分裂屬性;對該屬性中的值進行劣質數據檢測和修復,再將該屬性用于決策樹的分裂過程中;所花費的清洗代價達到了用戶設定的代價閾值時,不再對后續的分裂屬性進行清洗;結點中所有記錄所對應的類別標簽相同,或沒有分裂屬性的收益為正值時,停止對該結點的分裂,將其標記為葉子結點,其類別標簽為使得誤分類代價最小的類別. 上述過程中,基于分裂屬性收益和清洗代價的分步清洗算法見算法3.算法的輸入是待清洗的訓練數據集、用戶給定的清洗代價閾值、數據集中每個屬性對應的劣質數據檢測代價和修復代價. 首先,對根結點的收益與清洗代價比進行計算,選取比值最大的屬性作為分裂屬性(第1行~第5行).對該屬性中的屬性值進行劣質數據檢測和修復,計算剩余的清洗代價是否足夠對訓練數據集中該屬性的全部屬性值進行檢測:如果足夠,那么對該屬性的所有屬性值進行劣質數據檢測(第6行~第9行);如果不足夠,那么對該屬性部分屬性值進行檢測(第10行~第14行).在檢測出分裂屬性中包含的劣質數據后,對劣質數據進行修復,并計算剩余的清洗代價是否足夠對全部劣質數據進行修復:如果足夠,那么對該屬性中包含的所有劣質數據進行修復(第15行~第17行);如果不足夠,那么對部分劣質數據進行修復(第18行~第21行).然后,繼續為下一個結點尋找分裂屬性并清洗(第 22行).當清洗代價達到用戶給定的閾值或決策樹中全部結點都被清洗完畢后,返回清洗后的訓練數據集(第23行). 算法3.基于分裂屬性收益和清洗代價的分步清洗算法. 輸入:訓練數據集Dm×n,清洗代價閾值MaxCost,每個屬性x∈{1,2,…,n}的劣質數據檢測代價Det(ax)和修復代價Rep(ax); 輸出:清洗后的訓練數據集Dm×n. 算法3的時間復雜度取決于決策樹中的結點個數N、訓練數據集中的屬性個數n和記錄個數m.假設劣質數據檢測函數Detect(x)的時間復雜度為O(f(x)),劣質數據修復函數Repair(x)的時間復雜度為O(g(x)),當max(f(x),g(x))≥nlogn時,算法3的時間復雜度是O(Nmax(f(x),g(x)));當max(f(x),g(x)) 融合基于分裂屬性收益和清洗代價的分步清洗算法的代價敏感決策樹建立方法將收益大且清洗代價小的屬性選為分裂屬性并優先進行清洗.在決策樹建立的每一步中,分裂屬性被清洗完畢后再用于分裂.由于決策樹中層數低的分裂結點重要性高于層數高的分裂結點,該方法保證了決策樹結點分裂的有效性,有效降低了決策樹的誤分類代價和測試代價總和,使得決策樹在后續的分類任務中受訓練數據集中的劣質數據影響較小. 當用戶設定的數據清洗代價閾值較小時,融合基于分裂屬性收益的分步清洗算法的代價敏感決策樹建立方法可能會對清洗代價高的屬性優先進行清洗,使得能夠被清洗到的屬性個數較少,對劣質數據的清洗效果不大.因此,該方法不適用于這種情況.而融合基于分裂屬性收益和清洗代價的分步清洗算法的代價敏感決策樹建立方法優先對收益大且清洗代價小的屬性進行清洗,避免了優先清洗代價高的屬性,保證了數據清洗的效果和決策樹結點分裂的有效性.因此,該方法適用于這種情況. 當劣質數據比例較大時,融合基于分裂屬性收益和清洗代價的一次性清洗算法的代價敏感決策樹建立方法一次性清洗到的屬性不一定都會在后續的決策樹建立過程中被選作分裂屬性.該方法可能沒有清洗到決策樹建立過程中的某些分裂屬性,導致數據清洗過程對分類任務的作用不大.因此,該方法不適用于這種情況.而融合基于分裂屬性收益和清洗代價的分步清洗算法的代價敏感決策樹建立方法在決策樹建立的每一步中選擇分裂屬性,將其清洗完畢后再用于分裂.該方法保證了數據清洗的效果和決策樹結點分裂的有效性,有效降低了決策樹的誤分類代價和測試代價總和,使得決策樹在后續的分類任務中受訓練數據集中的劣質數據影響較小.因此,該方法適用于這種情況. 此外,為了方便讀者選擇最適合的數據清洗算法完成劣質數據上的代價敏感決策樹建立,表5從時間復雜度方面對本文所提出的3種清洗算法進行了比較,時間復雜度分析的詳細過程參見本文第3.1節~第3.3節. Table 5 Comparison of time complexity of three algorithms表5 3種算法的時間復雜度比較 為了驗證所提出方法的性能,本文從3個方面對所提出的3種融合數據清洗算法的代價敏感決策樹建立方法進行了測試:(1) 利用本文所提出的方法建立的代價敏感決策樹用于分類時產生的誤分類代價和測試代價總和;(2) 利用本文所提出的方法建立的代價敏感決策樹的分類準確率;(3) 利用本文所提出的方法建立的代價敏感決策樹的分類效率. 本實驗使用的數據集是UCI公測集上的6個經典數據集,其基本信息見表6.在實驗過程中,本文選用了劣質數據中的不一致數據進行實驗,根據在不同數據集上定義的函數依賴,向訓練數據集中人為注入錯誤.本實驗采用10折交叉驗證方法,隨機生成訓練集和測試集,并將在測試集上進行分類任務的結果取平均值作為最終的實驗結果. Table 6 Datasets information表6 數據集信息 所有實驗均在因特爾i7CPU@2.4GHz,8GB內存,1TB硬盤的電腦上完成,所有算法均用Python語言編寫. 本實驗分別對以下4種代價敏感決策樹進行了評估和比較. (1) T1:隨機對訓練數據集中的劣質數據進行清洗,再根據分裂屬性收益建立的代價敏感決策樹; (2) T2:采用融合基于分裂屬性收益的分步清洗算法的代價敏感決策樹建立方法建立的代價敏感決策樹; (3) T3:采用融合基于分裂屬性收益和清洗代價的一次性清洗算法的代價敏感決策樹建立方法建立的代價敏感決策樹; (4) T4:采用融合基于分裂屬性收益和清洗代價的分步清洗算法的代價敏感決策樹建立方法建立的代價敏感決策樹. 為了驗證所提出的代價敏感決策樹建立方法的有效性,本文對上述 4種代價敏感決策樹用于分類任務時產生的誤分類代價和測試代價總和(即TreeCost)進行了比較.首先,通過改變用戶給定的清洗代價最大值,測試分類任務產生的總代價所發生的變化.實驗結果如圖3所示. Fig.3 Comparison experiments varying MaxCost圖3 改變MaxCost值時的對比實驗 從圖3中能夠觀察到,決策樹T2和T4的總代價始終小于T1和T3,而T3的總代價往往小于T1.此外,從圖3(a)、圖3(d)~圖3(f)中可以看出:當用戶設定的清洗代價最大值MaxCost≤40%時,決策樹T4的總代價小于T2;當 MaxCost>40%時,T2的總代價小于 T4.在圖3(b)和圖3(c)中,當 MaxCost≤50%時, T4的總代價小于 T2;當MaxCost>50%時,T2的總代價小于 T4.這是由于當用戶給定的清洗代價較高時,只考慮分裂屬性收益而不考慮清洗代價,也能夠清洗到較多的分裂屬性;而當用戶給定的清洗代價較低時,如果不考慮屬性對應的清洗代價,可能會優先清洗收益高但清洗代價也高的分裂屬性,導致總清洗代價很快被用完,而能夠被清洗的分裂屬性卻很有限,從而影響了代價敏感決策樹的總代價. 因此可以得出結論:當用戶設定的清洗代價最大值較小時,代價敏感決策樹 T4的總代價最小,即采用融合基于分裂屬性收益和清洗代價的分步清洗算法的代價敏感決策樹建立方法建立的代價敏感決策樹最優;當用戶設定的清洗代價最大值較大時,代價敏感決策樹T2的總代價最小,即采用融合基于分裂屬性收益的分步清洗算法的代價敏感決策樹建立方法建立的代價敏感決策樹最優. 此外,沒有進行數據清洗而直接構建的代價敏感決策樹的總代價明顯高于融合數據清洗方法構建的代價敏感決策樹.由此可知,采用融合數據清洗的代價敏感決策樹建立方法大幅度節省了誤分類代價和測試代價.因此,數據清洗過程對于劣質數據上代價敏感決策樹的建立是十分必要的. 然后,本文通過改變訓練數據集中的錯誤率來評估分類任務產生的總代價所發生的變化.實驗結果如圖4所示. Fig.4 Comparison experiments varying error rate圖4 改變錯誤率時的對比實驗 從圖4中能夠觀察到:決策樹T3和T4的總代價始終小于T1和T2,而T2的總代價往往小于T1.此外,從圖4(a)、圖4(c)~圖4(e)中可以看出:當訓練數據集中的錯誤率小于等于40%時,決策樹T3的總代價小于T4;當錯誤率大于40%時,T4的總代價小于T3.在圖4(b)和圖4(f)中,當錯誤率小于等于30%時,T3的總代價小于T4;當錯誤率值大于30%時,T4的總代價小于T3.這是由于決策樹T3用到的一次性清洗算法并不能保證清洗到的屬性在建立決策樹的過程中被選做分裂屬性.在訓練數據集錯誤率較高的時候,可能導致許多存在劣質數據的分裂屬性并沒有被清洗到,從而影響了代價敏感決策樹分類時的總代價. 此外,通過圖4可以看出:當錯誤率上升時,總代價也不斷增大.這是由于訓練數據集中的劣質數據增多,使得代價敏感決策樹的結構更加復雜,結點數目增加,相應地,測試代價增大,總代價增大. 因此可以得出結論:當錯誤率較小時,代價敏感決策樹 T3的總代價最小,即采用融合基于分裂屬性收益和清洗代價的一次性清洗算法的代價敏感決策樹建立方法建立的代價敏感決策樹最優;當錯誤率較大時,代價敏感決策樹T4的總代價最小,即采用融合基于分裂屬性收益和清洗代價的分步清洗算法的代價敏感決策樹建立方法建立的代價敏感決策樹最優. 綜上所述,當錯誤率較大,而用戶設定的清洗代價最大值較小時,代價敏感決策樹 T4的總代價最小,即采用融合基于分裂屬性收益和清洗代價的分步清洗算法的代價敏感決策樹建立方法建立的代價敏感決策樹最優. 為驗證所提出的代價敏感決策樹建立方法的有效性,本文對 4種代價敏感決策樹的分類準確率進行了比較.實驗結果見表7,其中,MaxCost為0%的情況表示沒有對劣質數據進行清洗,直接構建代價敏感決策樹. Table 7 Experimental results of classification accuracy表7 分類準確率的實驗結果 從表7可以看出,代價敏感決策樹T1~ T4在分類準確率上相差極小.因此,在選擇代價敏感決策樹建立方法時,可以不必將分類準確率作為考慮因素.此外,沒有進行數據清洗而直接構建的代價敏感決策樹(即 MaxCost為0%)的分類準確率比融合數據清洗方法構建的代價敏感決策樹至少低7.23%(根據表7中的平均值計算).由此可知,采用融合數據清洗的代價敏感決策樹建立方法能夠有效提高決策樹的分類質量.因此,數據清洗過程對于劣質數據上代價敏感決策樹的建立是十分必要的. 為了驗證所提出的代價敏感決策樹建立方法的有效性,本文對 4種代價敏感決策樹的分類效率進行了比較.實驗結果見表8.從表8可以看出,代價敏感決策樹T1~T4在分類效率上相差極小.因此,在選擇代價敏感決策樹建立方法時,可以不必將分類效率作為考慮因素. Table 8 Experimental results of classification efficiency (ms)表8 分類效率的實驗結果 (毫秒) Table 8 Experimental results of classification efficiency (Continued) (ms)表8 分類效率的實驗結果(續) (毫秒) 綜合上述實驗,本文對所提出的 3種代價敏感決策樹建立方法進行了充分地比較.根據實驗結果,3種方法的具體適用情況見表9. Table 9 Applicable conditions of three methods表9 3種方法的適用情況 本文研究了劣質數據上代價敏感決策樹的建立問題.首先對決策樹、誤分類代價、測試代價、檢測代價和修復代價等相關概念進行了介紹,并對本文的研究問題進行了定義;然后,本文提出了3種融合數據清洗算法的代價敏感決策樹建立方法;最后,本文通過大量實驗驗證了 3種方法的總代價、分類準確率和分類效率,并給出了不同情況下最優的代價敏感決策樹建立方法.3.2 融合基于分裂屬性收益和清洗代價的一次性清洗算法的代價敏感決策樹建立方法


3.3 融合基于分裂屬性收益和清洗代價的分步清洗算法的代價敏感決策樹建立方法
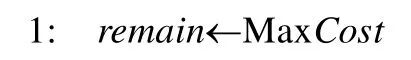

3.4 適用情況討論和時間復雜度比較
4 實驗評估
4.1 分類任務產生的總代價
4.2 分類任務的準確率

4.3 分類任務的效率



5 結 論

