時空依賴的城市道路旅行時間預測?
施 晉,毛嘉莉,金澈清
(華東師范大學 數據科學與工程學院,上海 200062)
隨著機動車保有量的激增,城市交通擁堵的狀況加劇惡化,從而導致出行效率低下、資源浪費、空氣污染等一系列問題,城市治堵已刻不容緩.合理引導出行路線可以在一定程度上緩解這一問題.隨著定位技術的發展與導航軟件的普及,越來越多的司機依賴導航軟件來規劃出行路線.旅行時間預測,即預測行駛路線的實際通行時間,可以幫助司機制定行程,避開擁堵路段,在交通管理、拼車、車輛派單等應用中具有重要意義.
定位技術的普及產生了移動對象的海量軌跡數據,例如出租車、公交車等車輛的行駛軌跡.最直接的旅行時間預測方法是通過匹配相似歷史軌跡數據來預測給定路線的旅行時間.此算法又可分為兩類:一類是直接通過歷史軌跡預測整段軌跡,但是易受到軌跡偏態分布性的影響,當綜合天氣、節假日等因素時,部分待預測軌跡可能無法找到可匹配的近似軌跡;另一類是將軌跡編碼為路網上連續的子路段,通過分別預測單個路段的旅行時間來估算給定路線的時間開銷,如圖1(b)所示.將軌跡映射到路段后,如果每個路段有足夠多的軌跡,可以有效緩解軌跡稀疏的問題.但是對各路段單獨預測會忽略了路段間上下游的信息,因此可能在一定程度上放大誤差.
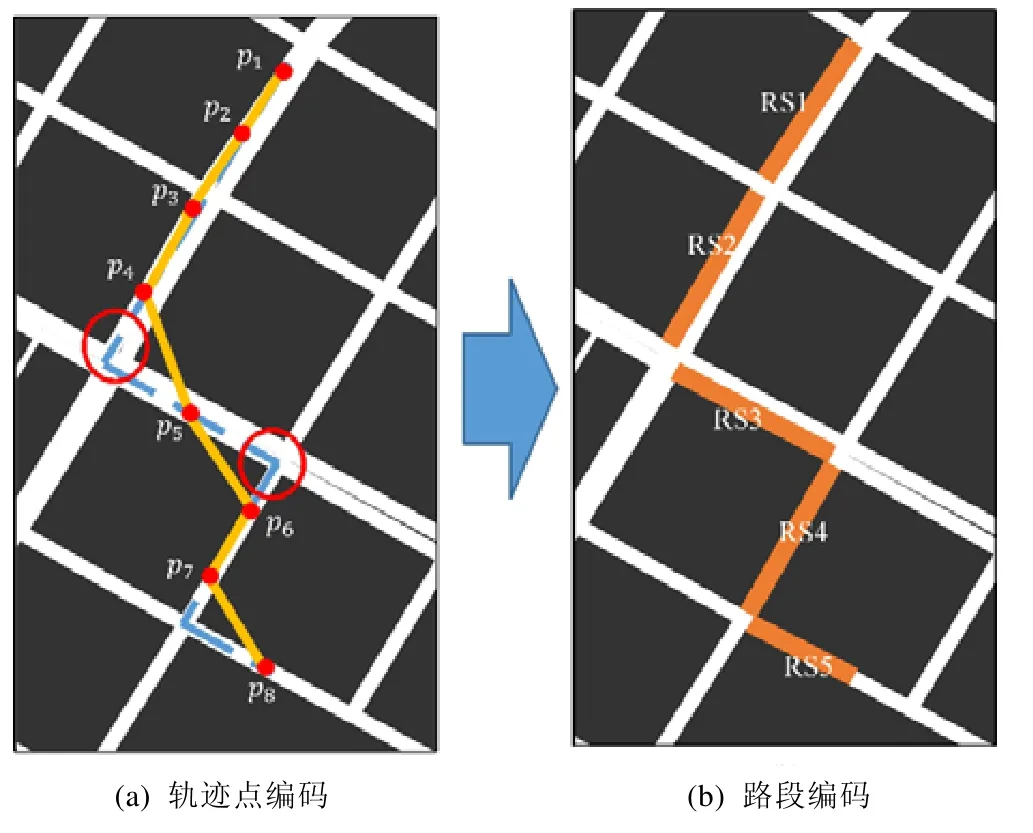
Fig.1圖1
車輛的旅行時間容易受到多重因素影響,包括路段依賴、時空相關性及其他外部因素.
1) 路段依賴主要由交通信號控制引起.例如,當行駛路線中存在綠波帶控制的路段時,旅行時間會大幅減小;此外,在路口右轉的等待時間比直行等待時間短;
2) 時空相關性體現在城市的擁堵路段,工作日早晚高峰的擁堵路段區域不同;節假日期間的擁堵路段區域與工作日的也不同;
3) 其他外部因素包括天氣狀況、司機的駕駛習慣、實時路況信息等.
由于上述因素之間相互作用關系復雜,因此旅行時間預測一直具有挑戰性.鑒于軌跡數據是不定長度的時間序列,傳統方法難以有效整合上述因素與軌跡數據.神經網絡模型是一種有效的方法.長短期記憶網絡(long short term memory network,簡稱LSTM network)在每個時間點共享參數,適于處理任意長度的時間序列.Wang等人[1]使用 LSTM 提取軌跡的時間依賴,并結合外部因素建模預測旅行時間.但是該方法依然存在不足:如圖1(a)所示,該算法將原始軌跡點均勻采樣成等距離的軌跡點作為輸入,可能會丟失部分路口的轉彎信息.例如,p4→p5→p6將被視作一條道路,從而在建模過程中引入錯誤的特征.
鑒于此,本文提出了基于路段編碼優化的深度旅行時間預測框架(road-segment encoding deep travel time estimation framework,簡稱REDTTE).REDTTE框架包括兩個階段.
(1) 針對使用原始軌跡(以經緯度坐標表示)作為輸入而引起誤差的問題,擬通過對路段建模并使用路段向量映射(road segment vectorization,簡稱RSV)模型將路段映射到低維向量中,保留路段間上下游依賴關系;
(2) 針對不定長序列數據難以處理以及外部特征較難引入的問題,結合神經網絡模型能夠處理不定長序列并且能夠捕捉軌跡時空特征的優勢,設計了長短期記憶網絡和卷積神經網絡(convolutional neural network,簡稱CNN)的混合模型對(LSTM-CNN-LSTM,簡稱LCL)預測旅行時間.
本文的貢獻主要有以下幾點.
(1) 受到詞嵌入(word embedding)技術的啟發,設計了RSV模型,融合神經網絡語言模型的處理思路至路段編碼,將路段映射到低維向量保留路段間的依賴關系.映射過程中,使用Skip-Gram模型對路段序列進行學習,確保具有上下游關系的路段向量間距離較近,無上下游關系的路段向量距離較遠.本文首次通過將深度表征學習引入改進路段的編碼方式,并將其應用于旅行時間的預測;
(2) 基于路段向量的編碼模式,設計了LCL模型用于預測旅行時間.該模型通過輸入組件將路段向量與其他外部特征(天氣、節假日)進行整合,通過LSTM與CNN的混合神經網絡分別提取時間、空間特征,在數據允許的情況下,還能將路況信息、道路限速信息、車輛型號等信息引入模型,提升預測精度;
(3) 結合RSV與LCL模型,提出了旅行時間預測框架REDTTE.通過使用出租車的軌跡數據訓練REDTTE框架,驗證了該框架的有效性.此外,基于真實數據集合的對比實驗結果表明,本文所提方法比對比算法的預測精度更高.
本文第1節介紹基于深度學習理論的軌跡序列處理技術及旅行時間預測的相關工作.第2節形式化定義相關概念,并介紹REDTTE的總體框架.第3節詳細介紹框架中兩個模型.第4節介紹本文所提方法在出租車軌跡數據集上的對比實驗結果.第5節總結全文并指出未來的工作思路.
1 相關工作
本節回顧基于深度學習理論的軌跡序列處理方法以及現有的旅行時間預測方法.
1.1 基于深度學習的軌跡序列處理技術
深度學習已廣泛應用在圖像處理、自然語言處理等多個領域.近年來,不少研究工作利用深度學習理論處理軌跡數據,其中最為普遍的是卷積神經網絡與循環神經網絡(recurrent neural network,簡稱RNN).
CNN通過卷積、池化等操作,可以提取網格結構數據中的空間特征[2].部分工作將軌跡數據轉換為網格數據使用CNN進行處理,有效提升了路段行駛速度與人流量預測的精度[3,4].RNN是專門處理時間序列數據的神經網絡模型[5].Dong使用RNN構建了一個自編碼器用于提取軌跡序列中的時間依賴特征,并分析司機的駕駛行為,在司機數量估算和軌跡分類上取得了較高的準確率[6].然而,傳統的 RNN模型僅由一個隱層記錄歷史信息,當輸入序列過長時會產生梯度消失以及梯度爆炸問題[7],導致難以處理長時間的依賴關系.LSTM 模型通過引入記憶單元存儲相關的歷史數據,有效緩解了難以捕捉長期依賴的問題[8].Song使用多層LSTM網絡模型提取軌跡數據上的時間依賴關系,用于預測城市的出行模式[9].
1.2 旅行時間預測
早期的旅行時間預測工作主要基于線圈傳感器所采集的數據,記錄車輛通過一個路段的行駛時間進行建模,來預測車輛的旅行時間[10-12].然而,由于線圈傳感器僅僅部署在城市的部分路段上,這類算法難以預測整個城市路網車輛的旅行時間.現有的工作大多使用浮動車的歷史軌跡對旅行時間進行預測,根據軌跡數據的處理方式不同,可以劃分為基于路段的旅行時間預測與基于路徑的旅行時間預測.
· 基于路段的旅行時間預測:將軌跡切分成路段,可以緩解軌跡稀疏帶來的影響.Jenelius針對低采樣率的軌跡數據使用概率建模,并用極大似然估計進行參數估計.考慮到外部因素的影響,模型將旅行時間視為一個多變量的正態分布[13].Yang通過時空相關的隱馬爾可夫模型對路段的時空依賴關系進行建模,對路段的旅行時間分布進行預測[14].該類算法未考慮結合多源的外部特征(如天氣、日期等)來提高算法的預測精度;
· 基于路徑的旅行時間預測:Rahmani根據浮動車的歷史軌跡數據提出了一種非參數的方法,通過對歷史軌跡的時間加權作為旅行時間估計結果[15].然而,直接基于歷史軌跡時間估計旅行時間會面臨軌跡稀疏問題.當待預測的行駛路線缺少與其對應的歷史軌跡時,該方法難以給出一個精確解.部分研究工作使用k近鄰搜索和加權平均的思想,通過查找相似的軌跡來減輕軌跡稀疏帶來的影響[16,17].Wang等人使用張量對映射到路段的軌跡數據進行建模,同時,利用張量分解重建技術引入路段間上下文關系的特征[18].
基于樹的模型可以整合多源的外部特征,Lam使用梯度提升決策樹(gradient boosting decision tree,簡稱GBDT)、隨機森林(random forest,簡稱RF)等多種樹模型預測旅行時間[19].Wang利用樹模型整合外部特征,結合時空相關的概率圖模型預測旅行時間[20].這兩個方法提高了預測精度,但因軌跡序列的長度不固定,傳統的機器學習模型難以處理這類數據.同時,軌跡數據是時空相關數據,這些模型不能有效提取數據中的時空依賴特征.
Wang等人提出了DeepTTE模型,結合CNN和LSTM提取軌跡數據的時空特征,并且整合Attention機制預測旅行時間[1].然而,由于該方法直接使用原始軌跡數據進行建模,在訓練過程中無法學習到路網的相關特征,容易引入錯誤特征.可以通過將軌跡映射到路段的方式引入路網特征,然而路段如果采用序號編碼無法反映路段間的上下游關系,需要對其進一步編碼.這與自然語言處理中的語言模型的處理思路類似.早期的自然語言處理中,大多采用 one-hot編碼對單詞進行表示.由于這一方法存在的巨大缺陷,Bengio提出使用三層神經網絡對語言模型進行建模[21],Collobert使用神經網絡語言模型生成詞向量,并在詞性標注、短語識別、語義角色標注等任務中表現良好[22].為了提升神經網絡語言模型在大型語料庫中的效果和性能,Mikolov提出了Skip-Gram模型[23],并推動了詞嵌入技術在這一領域的發展.由于基于負采樣的Skip-Gram模型能夠快速訓練,并且在大規模的數據集中具有較好的編碼效果,本文考慮將其引入用于路段編碼的表示優化.在此基礎上,采用LCL模型通過LSTM模型處理路段向量這一時間序列數據,并提取路段間的深層依賴關系,相比DeepTTE需先通過CNN提取軌跡點的轉彎行駛等信息,本文的方法不會放大軌跡點的定位誤差,因而有效提升了旅行時間預測精度.
2 概念定義與整體框架
2.1 概念定義
軌跡數據通過采集車輛行駛過程中的GPS數據獲得.
定義1(軌跡).一條軌跡Tra是帶有時間屬性的位置點序列,表示為Tra={p1,p2,…,pm},其中,每個位置點包含經、緯度信息以及記錄該位置點的時間戳,pi=(lngi,lati,timei).
由于軌跡數據以一定的時間間隔采集,且GPS定位技術本身也存在誤差,僅憑車輛的軌跡數據難以還原車輛真實的行駛情況.在對軌跡數據的預處理階段,常結合路網數據對原始軌跡進行地圖匹配,將車輛軌跡映射到路網中的真實路段.
定義2(路網).一個城市的路網以有向圖表示,即G=(V,R),其中:V為頂點集合,表示道路交叉口;R={r}為連接頂點之間路段的集合,其中,每個路段r包含路段標識符信息r.id以及路段長度r.dis.
將軌跡映射到路段后,軌跡點依次經過的路段序列可用來描述整條軌跡的信息.
定義3(路段序列).一個路段序列RS是通過地圖匹配將歷史軌跡序列Tra映射到一個有序路段序列RS={r1,r2,…,rn},其中,在一個路段上的連續軌跡點被映射到同一個路段r.
如果使用路段序列對軌跡進行編碼,各路段由其對應的id標識,此編碼丟失了路段之間的上下游關系,同時,也難以將其作為模型的輸入進行訓練.所以,我們使用路段向量序列對輸入軌跡進行編碼.
定義4(路段向量序列).路段向量集合是通過一定的映射方式f將路網中路段集合{r}映射到一個向量集合{rv};而路段向量序列RV則是由路段序列RS對各路段使用f映射獲得的向量序列,表示為RV={rv1,rv2,…,rvn}.
將路段向量序列與其他外部特征使用模型進行融合作為輸入特征,并以該段軌跡的旅行時間作為標簽,旅行時間預測問題可以轉換為一個監督學習的問題.
定義5(旅行時間預測).給定一段軌跡Tra={p1,p2,…,pm},對這段軌跡的旅行時間T(T=pmtime-p1time)進行預測,同時確保預測值T與真實值間的誤差最小化.此外,軌跡數據的時間戳僅用于結果的驗證,在預測過程中會將其去除.
2.2 總體框架
REDTTE框架包括3部分:軌跡預處理、模型訓練、在線預測,如圖2所示.
在軌跡預處理階段,通過地圖匹配,將歷史軌跡數據映射為路段序列,該序列將作為RSV模型訓練的輸入;
在模型訓練階段,主要針對RSV以及LCL模型進行兩階段訓練.第1階段的訓練過程中,將軌跡序列輸入到RSV模型進行訓練,使得路網中每一個道路id映射到一個低維向量.RSV模型訓練完畢后,對路段序列所有路段使用該模型進行映射;第2階段訓練LCL模型的3個組件:首先,通過特征嵌入方式將路段向量與天氣、節假日等外部特征相結合,作為模型的輸入;輸入組件對輸入特征進行整合后,將輸入的特征序列通過深度特征提取組件的LSTM和CNN模型獲取時空相關特征;最后,由LSTM和均勻池化組成的預測組件預測旅行時間進行;根據預測結果與真實值的誤差,LCL模型的訓練可通過反向傳播調整模型參數;
在線預測階段,使用訓練好的模型參數進行預測.可以直接輸入預測軌跡,也可以使用路段序列作為輸入.除軌跡數據以外,預測階段同樣需要輸入外部特征.天氣和節假日等外部特征可以通過天氣預報等信息提前獲得.REDTTE框架輸入的序列數據本質上是路段數據,因此,REDTTE框架也可以結合路況信息作為外部特征來提升預測精度.
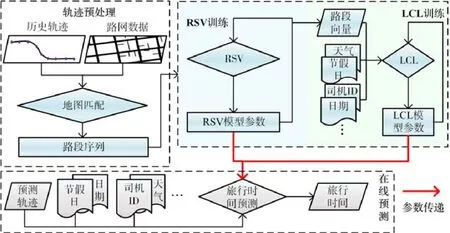
Fig.2 REDTTE’s global architecture圖2 REDTTE整體框架圖
3 模型概述
3.1 路段向量映射
將歷史軌跡通過地圖匹配方式轉換為路段序列RS={r1,r2,…,rn},其中每個路段有對應的路段序號r.id以及長度r.dis.由于僅靠路段序號無法辨識路段之間的上下游依賴關系,該編碼方式在一定程度上丟失了重要軌跡的信息.同時,若直接將序號作為模型的輸入,模型可能會認為序號相近的路段具有上下游關系,而這與事實不符.因此,需要一種方法將路段映射到低維的向量中.
one-hot編碼是一種簡單的映射方法.如后文圖4所示,輸入一個L維的向量,L為類別的數量,其中大部分項值為 0,只有與序號對應的項值為 1,表示當前路段.但這一編碼方式無法描述相鄰路段關聯性.另一種編碼方式使用每個路段中心點的經、緯度坐標來表示一個路段,但是該編碼無法識別雙向車道的上下游路段.
詞嵌入技術將詞匯映射到低維向量,語義相近的詞所對應的向量的距離較近,這與本任務的目標較為貼切,因此我們在 RSV模型中引入基于負采樣 Skip-Gram模型對路段進行映射,其主要思想是:對于一個輸入路段,預測其前后T個路段.這實質上是一個多標簽(multi-label)問題,可以通過負采樣生成負樣本的方式轉變成回歸問題.
首先,對路段序列使用滑動窗口模型生成訓練樣本,如圖3所示.對一個路段序列使用滑動窗口技術,當窗口指針指向r4向量,窗口大小為2時生成4個正樣本.
隨后構造中心路段的偽鄰居路段作為負樣本,負樣本的生成根據每個路段出現的頻次加權采樣生成,出現頻率越高的路段越容易被采樣生成負樣本.路段被采樣到的概率如下:

其中,freq(ri)函數用于統計路段出現的頻次,這里引入了拉普拉斯修正防止部分路段因缺失數據而不被采樣.
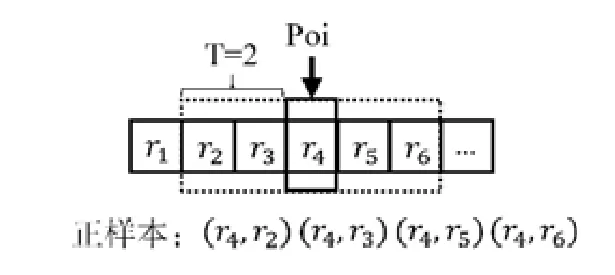
Fig.3 Example of sliding window model圖3 滑動窗口模型示意圖
樣本打分模型應能根據映射到的隱層信息,對正負樣本給予正確的判斷,即判斷出正確的具有上下游關系的路段,因此需要模型對輸入的樣本對進行打分.
圖4為樣本打分模型,主要分為輸入層、隱層和輸出層.輸入層為中心路段和鄰近路段(或偽鄰近路段)的one-hot編碼,分別為rc和rn.隱層h通過輸入層和矩陣WLH計算獲得,即h=f(r)=σ(WLHx+b),其中:b為該層的偏置向量;σ為激活函數,通常使用sigmoid函數σ(x)=1/(1+e-x).中心路段和鄰近路段分別采用不同的參數映射到隱層,即.通過矩陣將輸入映射到隱層向量后,對兩個隱層向量進行按元素相乘操作,并通過激活函數限制其大小,最后對向量進行求和,得到一個分數yscore.模型訓練完成后,中心路段的隱層為所求的低維向量,而輸入層到隱層的映射f就是所求的映射.
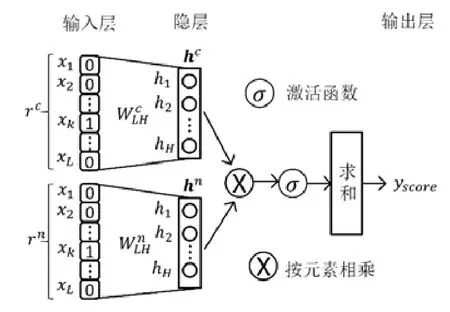
Fig.4 Scoring model圖4 樣本打分模型
RSV模型同時對輸入的正負樣本進行打分,并控制其比例為1:k.每次迭代,對輸入的一個正樣本對和k個負樣本對同時使用打分模型進行打分.打分模型的輸入為(ri,rj),模型需要最大化正樣本分數的同時最小化負樣本的分數,目標函數為

其中,Nei(ri)表示ri的相鄰路段,Neg(ri)表示對ri負采樣生成的所有路段.條件概率表示為
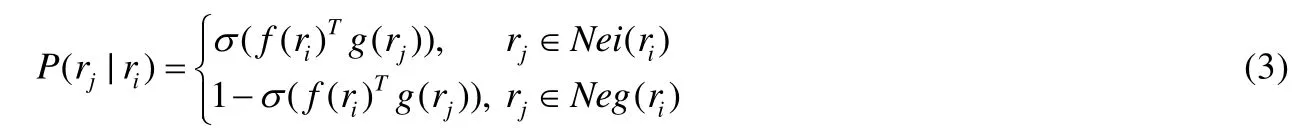
f為將道路id映射到路段向量的函數,g為輔助函數,兩函數映射后的向量維數相同,σ(x)為sigmoid函數.可以看出,目標函數存在大量的連乘.為便于計算,這里對L取對數,目標函數變為
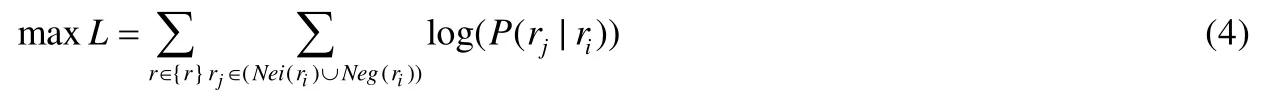
通過將歷史軌跡的路段向量通過RSV模型進行訓練,可以得到一個f將道路id映射到道路向量rvi中.通過對映射到向量空間的路段向量進一步觀察發現:具有上下游關系的路段映射到向量空間后,向量間的距離比沒有上下游關系的路段向量更近.因此,通過RSV編碼能夠很好地保留路段間的上下游依賴信息.
3.2 混合神經網絡
LCL模型的框架如圖5所示,模型分為3個組件:輸入組件主要用于結合外部特征、路段序列及其統計量(如出發時間、路段長度等)生成下一階段模型的輸入;深度特征提取組件主要用于提取輸入數據中的時空特征;預測組件根據提取出的高維度特征,結合LSTM模型和均勻池化層對旅行時間進行預測.
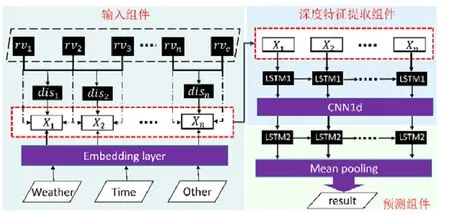
Fig.5 LCL architecture圖5 LCL模型框架圖
3.2.1 輸入組件
前面使用RSV模型將每個路段id映射到一個路段向量中,因此,將每個路段序列映射為路段向量序列RV={rv1,rv2,…,rvn,rve}作為特征組件的部分輸入.其中,為了標志軌跡序列的結尾,幫助模型對軌跡終點的判斷,引入零向量rve作為每條軌跡的終止向量.由于交叉路口的特征通常由兩個路口進行表示(例如圖1(b)中的RS2→RS3表示左轉,RS3→RS4表示右轉),因此,這里將兩個路段向量合并為一個向量作為輸入,即RVcombine={(rv1,rv2),(rv2,rv3),…,(rvn,rve)},合并后的向量長度與輸入的向量序列長度一致(為n).考慮到軌跡在不同路段的行駛距離是一個重要因素,尤其對于起始路段以及終止路段.起始及終止路段通常位于道路的中間部分,直接使用路段長度會增大模型估計的旅行時間.鑒于此,輸入組件計算目標軌跡在每個路段上的長度disi,并將其作為特征輸入.
模型的輸入組建將一些外部因素(如天氣、節假日等)與路段向量相結合,其中,天氣數據包含最高溫、最低溫、天氣狀況.與此同時,由于旅行時間預測的請求通常帶有出發時間,而出發時間是一個很重要的影響因素,考慮將一天劃分成28 800個時間槽作為特征輸入,每個時間槽對應了3s的時間間隔.由于城市的交通狀況具有一定的周期性,通常周期為一周[16],因此引入每周的天數作為輸入的特征.
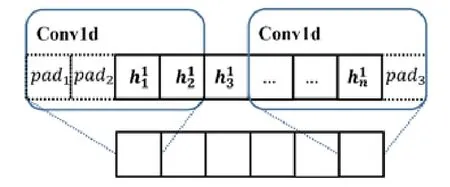
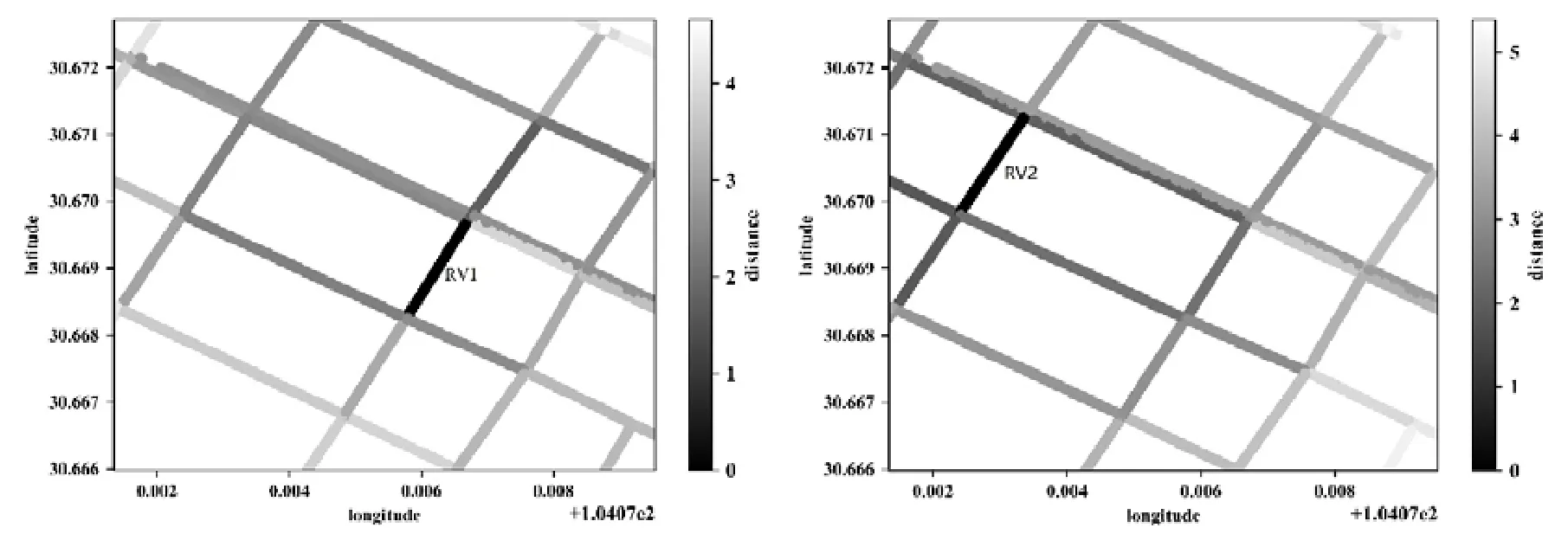
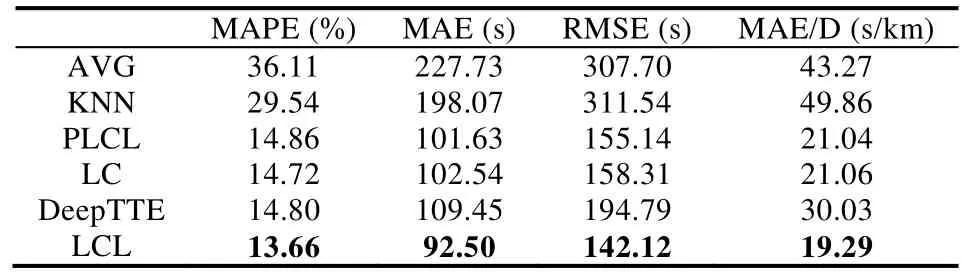
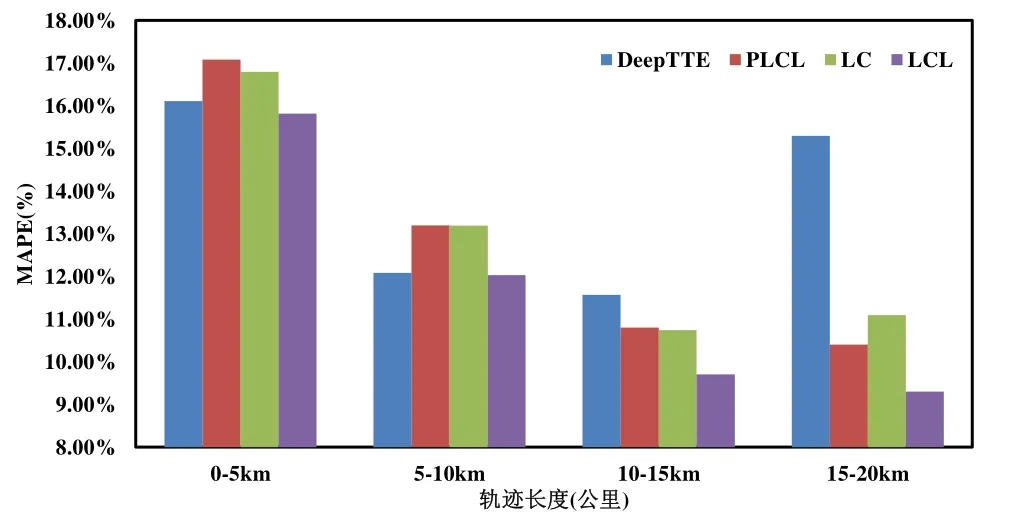
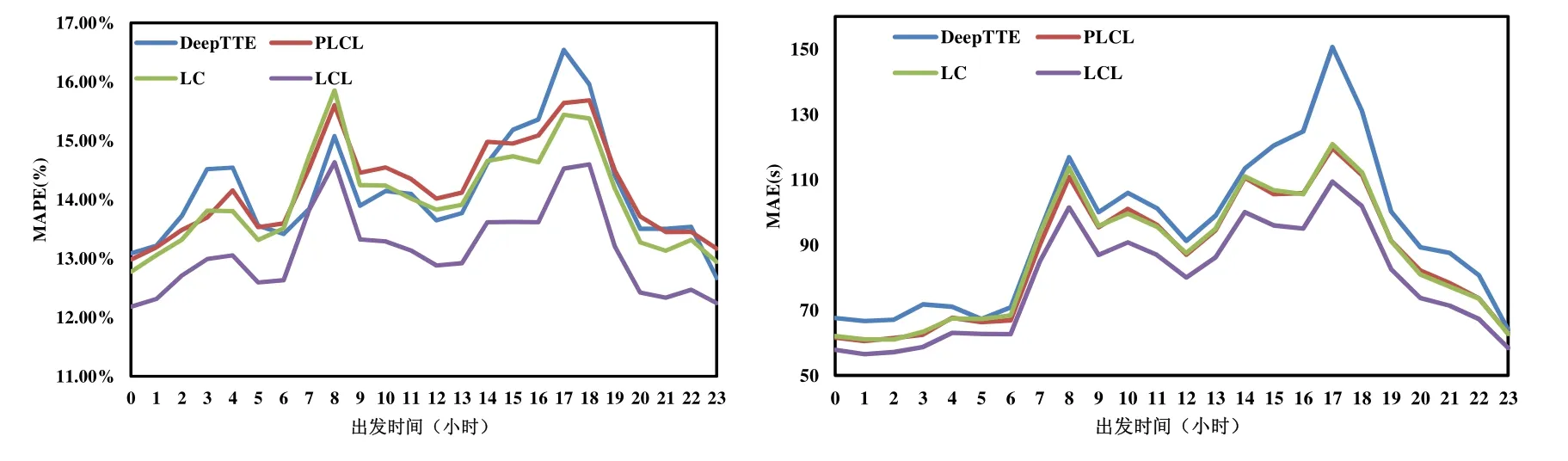
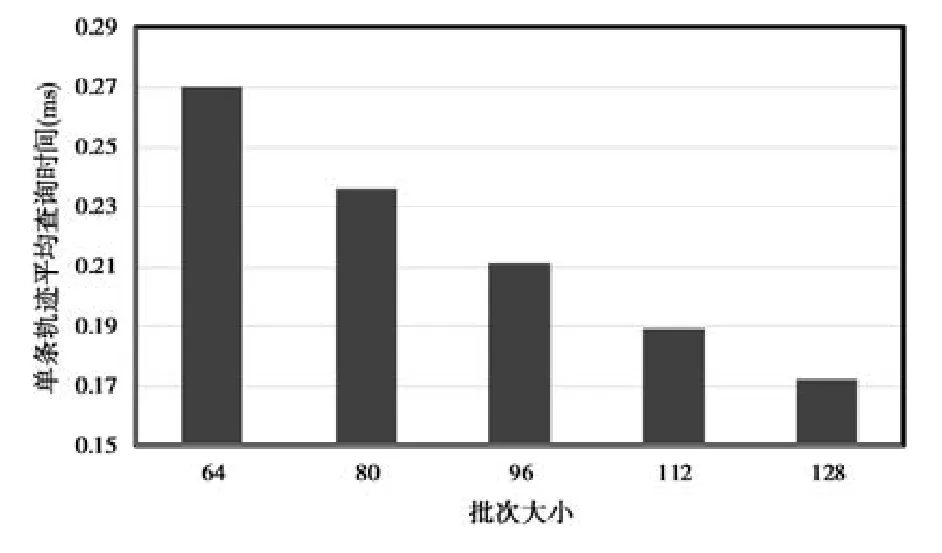
上述特征除了最低溫度和最高溫度外都是類別變量,不能直接將其作為 LSTM的輸入,采用Gal的特征嵌入方法將類別特征轉換為低維向量[20].類別特征c∈[C]通過參數矩陣WCE映射到空間RE中.其中,C為類別的數量,E為低維向量的維數,通常情況下,E< 輸入組件最后將以上特征進行整合,作為模型組件的輸入,表示為X={X1,X2,…,Xn},其中,Xi={rvi,rvi+1,disi,weather,time,…}.此外,司機畫像、車輛型號等信息同樣可以通過特征嵌入的方式進行引入,實時的路況信息和道路限速信息的引入方式與路段長度的引入方式一致. 3.2.2 深度特征提取組件 深度特征提取組件由兩層模型組成:第 1層循環神經網絡通過特征提取的方式挖掘路段向量之間的隱含關系,例如左轉、右轉、直行等特征;第 2層卷積層能夠挖掘更高層次的路段依賴關系,同時提取出更豐富的特征,如綠波帶. 鑒于使用路段向量對軌跡進行編碼,獲得的路段向量序列長度是不固定的,為提取路段向量之間的前后依賴,考慮使用循環神經網絡提取這部分的依賴特征. LSTM 的整體結構如圖6所示,它包括輸入層、隱層和輸出層,每個時間點共享同一個參數.當前時間點的隱層是由上一個時間點的隱層和當前時間點的輸入所決定的.這樣的結構使 LSTM 能夠保存前序時刻輸入的特征,從而提取輸入數據中的時間依賴關系,并處理不定長度的輸入序列.由于隱層的參數受到當前輸入和前一個時間點隱層的共同影響,因此無法通過普通的反向傳播算法進行訓練,采用隨時間的反向傳播算法(back propagation through time,簡稱BPTT)對模型進行訓練. Fig.6 LSTM structure圖6 LSTM網絡結構 圖6是LSTM的內部結構圖,與RNN相比多了一個記憶單元Ct,用于記憶歷史信息.LSTM的內部結構主要由遺忘門、輸入門、輸出門組成. · 遺忘門用于在原始記憶單元中丟失部分信息,根據上一時間點的隱層信息以及當前的輸入,通過激活函數輸出遺忘元素的概率: · 輸入門通過類似的結構篩選出輸入數據中需保存至記憶單元的數據,并將其與通過遺忘門之后的記憶單元的數據相加作為記憶單元的輸出: · 最后,隱層的數據通過輸出門的數據與新的記憶單元的數據進行逐點相乘計算得到: 在實際訓練過程中,將特征組件得到的特征序列X={X1,X2,…,Xn}依次輸入到第1層的LSTM中,并將隱層數據提取出來作為下一層模型的輸入. 通過 LSTM提取上下路段間的時間依賴后,LCL模型通過卷積神經網絡挖掘多個路段間的依賴關系來豐富特征的多樣性,同時挖掘出路段間更深層次的聯系(如綠波帶等信息). 考慮將卷積層引入,用以提取空間特征.由于輸入的隱層序列是一維的序列,因此使用一維的卷積核對序列進行卷積操作.卷積的操作如圖7所示,以大小為kn=4的卷積核為例,其中,填充向量pad用于保證輸出序列的長度和輸入序列的長度一致,個數為kn-1.我們加入了與輸入的隱層h1同維數填充零向量,卷積層的輸入為,那么其輸出為,其中,每個元素表示為 Fig.7 Conv1d diagram圖7 Conv1d示意圖 3.2.3 預測組件 LSTM 模型不僅可以用于特征提取,其輸出同樣可以用于回歸、分類等任務.在預測組件中,模型將上一層卷積層的輸出作為第3層LSTM的輸入.為了在旅行時間的預測過程中考慮到所有的路段,該層LSTM依舊使用與第1層的LSTM一致的多對多網絡結構,并將隱層的信息作為均勻池化層的輸入. 由于最后輸出的序列長度與輸入的路段序列長度相同,但旅行時間預測的目標是一個實值,因此使用均勻池化將LSTM隱層的輸出映射為一個實值作為最終預測的旅行時間: 3.2.4 損失函數 鑒于長度越長的軌跡預測誤差時間越大,直接使用MAE作為損失函數會使模型更加偏重于旅行時間較長的軌跡.為保證模型同時優化短途和長途的軌跡,采用相對百分誤差的絕對值(mean absolute percentage error,簡稱MAPE)作為模型的損失函數: 根據損失函數提供的梯度信息,模型參數可以通過反向傳播不斷學習調整. 為了驗證 REDTTE框架的有效性,本文基于出租車軌跡數據集進行對比實驗以及各模塊的有效性驗證實驗.通過與 AVG,KNN等傳統旅行時間預測算法的對比實驗,驗證深度學習模型處理旅行時間預測問題的優越性.通過與 DeepTTE算法的對比實驗來驗證 REDTTE模型結構的有效性.此外,為驗證路段向量編碼以及深度特征提取組件的有效性,分別執行了與PLCL(point LCL)及LC算法的對比實驗. 4.1.1 數據集 · 軌跡數據:本文使用滴滴開放的蓋亞計劃(https://outreach.didichuxing.com/research/opendata/)數據集.該數據集提取成都2016年11月30天的車輛軌跡數據,包含10億GPS坐標點、400多萬條軌跡.由于數據集每天采取不同的哈希函數對司機ID進行脫敏,因此,實驗中無法使用司機ID作為外部特征; · 路網數據:為了保證數據的一致性,路網數據使用成都市 2016年的 OpenStreetMap(https://www.openstreetmap.org)數據,對實驗數據進行地圖匹配后獲得5 856條路段; · 外部因素:成都市的天氣數據通過爬蟲抓取,包含天氣狀況(晴天、雨天等4種天氣狀態)、最低氣溫與最高氣溫等信息. 4.1.2 實驗環境 本文使用python語言完成全部實驗的編寫,并使用基于python的深度學習框架Pytorch 0.3框架實現了部分模型的編寫.硬件環境為160G內存,兩個8核的Intel Xeon Silver 4110處理器以及一個NVIDIA Tesla K80 GPU.模型的訓練與測試均在GPU上進行. 4.1.3 評測指標 為了更全面地評估框架預測旅行時間的效果,本文使用了 4種評測指標:平均絕對值誤差(mean absolute error,簡稱 MAE)、均方根誤差(root mean square error,簡稱 RMSE)、MAPE(見公式(13))、MAE/D. 由于MAE會受到路徑長度的影響,即越長的路徑旅行時間越長,因此誤差可能就會越大.考慮將MAE與軌跡長度的比值,即MAE/D,作為衡量算法在每公里的預測誤差時間. 4.1.4 參數設置 · RSV:考慮到部分路段長度較短,在采樣的過程中軌跡可能會跳過這些路段,因此,基于實驗數據集將滑動窗口大小設置為 3,正負樣本的采樣比為1:5.映射到向量空間的維度設為10維,為加快訓練速度,訓練過程中采取了批梯度下降,批量設為50,初始學習速率設為0.025,樣本訓練一個周期; · LCL:輸入組件部分,將每周的天數映射到3維的向量,小時映射到10維的向量,時間槽映射到40維的向量.深度特征提取組件的LSTM的隱層維數為84,CNN的通道數為36,卷積核大小為4.預測組件的LSTM與上一層的LSTM參數一致. 為加速模型的訓練,我們對數據集進行分批訓練,模型的批量為64,初始的學習速率為0.002,模型訓練10個周期. 4.1.5 對比算法 · Avg算法是作為旅行時間預測對比的一種基準算法,算法將一天以 10分鐘的間隔劃分成 144個時間槽.通過計算軌跡長度與對應出發時間的歷史軌跡平均速度的比值作為旅行時間.在計算過程中同樣考慮到了每周的天數帶來的影響,例如,周一的旅行時間會考慮歷史的周一在該時間槽內出發的軌跡的平均速度; · KNN算法是一種非參數的算法,算法根據待查詢軌跡的起點和終點查詢與其起點和終點相近的歷史軌跡,根據鄰近軌跡與查詢軌跡的出發時間和節假日、軌跡長度等信息,對鄰近軌跡的旅行時間進行加權和作為最后預測的旅行時間.在實驗過程中,選取了k=10作為具體的參數,當算法查詢不到足夠數量的鄰近點時,會同時擴大起點和終點的搜索范圍,直到找到足夠的鄰近軌跡; · PLCL(point LCL)將LCL模型的輸入由路段向量序列替換為每個路段的中心經緯度坐標點,其余的參數及特征設置與LCL一致; · LC為LCL模型的簡化版本,LC模型去掉了第3層的LSTM,將卷積層的輸出直接連接池化層,輸出最后的旅行時間.除此之外,其余參數特征與LCL一致; · DeepTTE[1]是當前主流的旅行時間預測算法.算法使用經、緯度作為模型的輸入,利用混合神經網絡分別提取軌跡數據的時空依賴.同時,通過Attention機制以及特征嵌入的方式將外部因素引入.這里,我們使用算法開放的源代碼與算法表現最優的參數,并在實驗數據集下進行微調優化.模型使用的外部特征與LCL使用的外部特征一致. 為了展示路段向量的表示效果,選取成都青羊區的部分區域進行可視化展示.圖8所示為RV1,RV2兩個路段向量的示意圖.其中,橫縱坐標分別表示經緯度.圖中反映了該區域的路網情況,以顏色的深淺表示對應路段的路段向量與示意路段向量間的距離.黑色表示距離為零,顏色越淡表示距離越遠.從圖中可以看出:路段向量的表示方式保留了路段上下游的依賴關系,與目標向量具有上下游關系的路段,其路段向量距離較近,而不具有上下游關系的路段向量則距離較遠. Fig.8 Schematic plot for road vector圖8 路段向量示意圖 為了驗證算法的準確率,將數據集中前23天的數據作為模型的訓練數據,后7天的數據作為驗證數據.表1為算法及對比算法在該數據集下各項指標的預測結果,可以看出,本文提出的方法在各項誤差指標中均擁有最低的誤差. Table1 Error comparison表1 誤差對比 通過 PLCL和 LCL的誤差對比可以發現:將路段向量替換為經緯度坐標后,模型的誤差值上升,這證明了RSV算法的有效性.同樣,通過LC和其他算法的誤差對比可以發現,直接使用深度特征提取組件的輸出預測旅行時間具有較高的準確率.通過LC及PLCL與DeepTTE的對比可以發現:使用REDTTE的部分模型結構預測旅行時間具有較好的效果,甚至在部分指標的對比中優于DeepTTE的表現. 為了驗證DeepTTE,LCL,LC及PLCL算法在不同影響因素下的敏感性以及預測精度,分別統計了不同軌跡長度以及不同出發時間對上述算法的影響.圖9為不同軌跡長度對上述算法的影響,橫坐標為軌跡的長度,縱坐標為MAPE.可以發現:在路段長度較短時,真實的旅行時間往往較短,小的偏差會導致MAPE值增大.因此,上述算法均在較短的軌跡上具有較大的MAPE值. Fig.9 Influence of trajectory distance on each algorithm圖9 軌跡長度對各算法的影響 為評測出發時間對各算法的影響,分別對比工作日與節假日的 MAE和 MAPE兩個指標的算法效果.如圖10、圖11所示,其中,橫坐標是以小時為單位劃分的時段,縱坐標為對應的各項指標值. Fig.10 Influence of start time (weekday) on each algorithm圖10 出發時間對各算法的影響(工作日) Fig.11 Influence of start time (weekend) on each algorithm圖11 出發時間對各算法的影響(節假日) 可以看出:在工作日的早晚高峰期間,算法的誤差普遍偏高.通過對早晚高峰期的數據分析,可以發現旅行時間在這一時間段擁有較高的方差,因此難以做到準確的預測.產生這一現象的主要原因是:早晚高峰期間道路情況多變,各模型因未引入路況信息作為外部特征,難以捕捉實時變化的道路擁堵狀況.在節假日期間,由于路況復雜多變,各算法的誤差要大于工作日的預測誤差. 旅行時間預測通常應用于實時性需求較強的環境中,因此其運行效率是一個重要的參考指標.為了驗證算法的執行效率以及分布式場景下的可擴展性,通過在 GPU上運行算法,設立了不同的批次模擬并行環境.同時,考慮到設備性能波動而產生的時間誤差,實驗分別在不同批次下對 100萬條軌跡進行查詢,并統計其平均時間開銷.查詢實驗的硬件環境與第4.1.2節的實驗環境一致. 圖12為算法在 64,80,96,112,128批次下平均單條軌跡的查詢時間效果圖,橫軸為批次大小,縱軸為單條軌跡的平均查詢時間.從實驗結果可以看出:算法對于單條軌跡的響應時間均為毫秒級,具有較高的實時性;并且隨著批次的增多,平均單條軌跡的查詢時間隨著線性減少.這是因為算法在運行過程中僅需要進行路段序列的映射以及 LCL模型的推斷(inference),且整體模型可以離線存儲至內存中.因此,算法能夠在大規模分布式環境下進行拓展. Fig.12 Average query time for a single trajectory on different batch size圖12 不同批次下單條軌跡的平均查詢時間 針對傳統的旅行時間預測模型難以引入多源特征的問題,本文提出了一種兩階段的旅行時間預測框架REDTTE.框架的第1階段通過引入Skip-Gram模型將路段映射到向量空間,可以有效地捕捉路段之間的依賴關系;第 2階段針對路段向量序列的特性,整合天氣日期(工作日/節假日)等外部特征,設計了深度模型用于預測旅行時間.基于海量軌跡數據的實驗結果表明,REDTTE框架因能較好提取路段間上下游依賴關系而具有較高的旅行時間預測精度.考慮到在節假日與工作日的早晚高峰時期模型的預測誤差較高,未來擬通過對路況建模,預測未來路段序列中每個路段的速度信息,將其與路段向量共同輸入以提高模型的預測精度.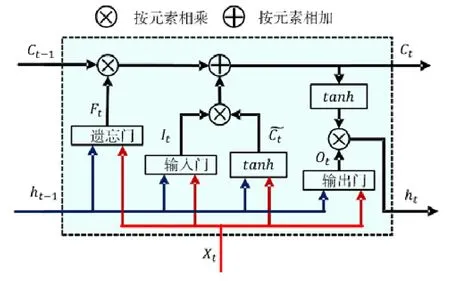






4 實 驗
4.1 實驗設置
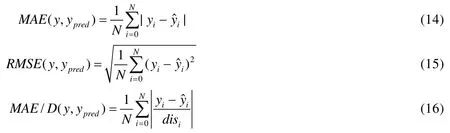
4.2 實驗效果
4.3 性能測試
5 結束語

