電池剩余放電時間預測

陳東陽 柳林思青 朱銘鋅

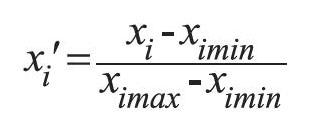
摘要：鉛酸電池在交通、電力、軍事等各個領域都起到了非常重要的作用，因而預測電池剩余放電時間具有一定的實際意義。依據采樣數據，運用BAS-BP和曲線擬合的方法建立了預測電池剩余放電時間的數學模型。利用神經網絡得到9.8V時20A到100A電流強度下電池的剩余放電時間，然后利用MATLAB擬合工具箱得到電池剩余放電時間的計算公式。

關鍵詞：BAS-BP;曲線擬合;電池剩余放電時間

鉛酸電池是一種蓄電池。由于其壽命長、維護方便等優良性能被廣泛用于各個領域。當電池在恒定電流強度下放電時，電壓與放電時間的增加而下降，直至最低額定保護電壓。在使用電池時，必須要了解電池的剩余放電時間，因此預測電池的剩余放電時間是非常重要的。

1 數據的來源及處理

參考2016年全國大學生數學建模競賽C題，利用題目所給數據，對數據進行預處理。由于電池剩余放電時間、電壓以及電流強度的單位和變異程度不同，為了消除量綱影響和變量自身差異的影響，故對數據進行歸一化處理，原理[1]為：

2 電池剩余放電時間模型的建立

原始的BP神經網絡存在很多局限性，完全依靠誤差來調整網絡的權值和閾值[3]，導致網絡的性能不是很好，對結果會產生較大的影響。利用天牛須算法為網絡選取初始權值和閾值可以提高網絡的性能[2]。

以題目中所給的6531個采樣數據為總樣本，6481個樣本作為訓練集，50個樣本作為檢驗集，選取相對誤差這一指標評價模型的性能。

BP神經網絡采用輸入神經元個數input為2，輸出神經元個數output為1，由隱含層神經元經驗公式：

可確定隱含層神經元個數 ，比較每個神經元下的相對誤差，如圖1所示：

選取相對誤差最小時的隱含層神經元個數，h的值為6，此時相對誤差為0.1917。

BAS-BP 網絡預測模型訓練集的擬合結果如圖2所示，預測數據與實際數據對比可以看出，BAS-BP模型預測結果非常逼近真實值。

利用上述建立的BAS-BP模型預測出9.8V時不同電流強度條件下的電池剩余放電時間。對求得的數據利用MATLAB的數據擬合工具箱進行擬合，發現在眾多函數中，Power函數擬合的效果最好，均方根誤差RMSE為26.83，R-square為0.9992。擬合的結果如下：

利用建立的模型，可以預測當電壓為9.8V時，任意電流強度下的剩余放電時間。利用上述方法，同樣可以計算出不同電壓下，不同電流對應的剩余放電時間計算公式。

參考文獻：

[1]羅玉彬，牛冉雯.樣本數據歸一化對GPS高程轉化結果的影響分析[J].測繪通報，2013 （8）：33.

[2]王甜甜，劉強.基于BAS-BP模型的風暴潮災害損失預測[J].海洋環境科學，2018，37 （03）：457-463.

[3]袁冰清，程功，鄭柳剛.BP神經網絡基本原理[J].數字通信世界，2018 （08）：28-29.