商用車傳動軸振動問題分析

李海建，徐海軍，梁金玲

（柳州五菱汽車工業有限公司，廣西 柳州545007）

0 引言

在后橋傳動系統的振動中，有很大一部分是由于傳動軸的振動引起的。傳動軸的振動影響整車的舒適性，人坐在車內可以明顯的感受到傳動軸對地板的振動。傳動軸的振動不僅影響整車舒適性，還對傳動軸零件的耐久產生不利的影響。比如十字軸軸承燒蝕，中間支撐橡膠開裂，中間支撐支架開裂，更為嚴重的就是使得與傳動軸連接的變速箱或者后橋零件出現故障[1]。本文針對某商用車在售后市場反饋地板振動過大，人耳噪聲過大等問題進行研究，初步判斷為傳動軸振動過大引起的。本文針對傳動軸振動噪聲過大的問題進行了優化分析

1 傳動軸振動原因分析

傳動軸作為高速旋轉件，如果傳動軸動不平衡量過大，那么在高速旋轉的時候傳動軸由于離心力的作用就會發生彎曲振動，這對整車的舒適性能是極為不利的。如圖1所示，傳動軸一階振動主要來源于傳動軸自身的不平衡，而二階振動則是由于傳動軸之間采用了不等速萬向節。不等速萬向節在傳動過程中會出現轉速和扭矩的波動，不等速萬向節產生的附加彎矩按照周期180°的正弦波變化，附加彎矩忽大忽小的變化很容易產生和它相連接的零件的振動[2]。為了盡量減少傳動軸不等速萬向節產生的振動，必須在設計初期就使得傳動軸的當量夾角比較小。導致傳動軸振動過大的因素還有傳動軸臨界轉速不符合設計要求；傳動軸與變速箱連接的法蘭或者與后橋差速器連接的法蘭徑向跳動比較大，不符合設計要求；發動機輸出的扭矩波動與傳動軸的彎曲模態耦合；中間支撐在怠速的時候上、下剛體振動會引起起步振動。這些都是需要在傳動軸的設計過程中需要解決的問題。

圖1 后橋傳動系統

2 影響傳動軸振動因素的計算校核

2.1 傳動軸殘余不平衡量值的確定

根據ISO 1940《旋轉設備動平衡標準》規定，汽車傳動軸平衡精度等級為G40，對應的G取值40，但是由于我國汽車技術的高速發展以及城市道路的改善，對汽車高速性能的要求越來越高。因此目前主機廠推薦采用G16平衡品質等級。在傳動軸總成裝配完成后，必須做動平衡檢測，在傳動軸軸管上焊接平衡塊，減小剩余不平衡量到滿足要求的范圍內。殘余不平衡量值計算公式如下：

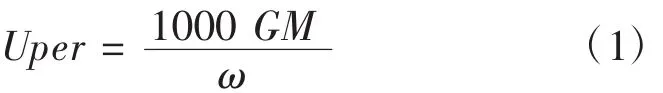
式中，G表示平衡精度（mm/s）；ω表示角速度（rad/s）；Uper表示許用不平衡量（g·mm）；M 表示傳動軸質量（kg）；其中（r/min）。

本文所研究的傳動軸最高轉速n=6 000 r/min，質量M=9.8 kg代入（1）式中得到傳動軸的殘余不平衡量值Uper=254.6 g·mm，每端許用不平衡量值Uper/3=85 g·mm在傳動軸軸管上焊接平衡塊如圖2所示，使得傳動軸動不平衡量滿足設計要求。

圖2 傳動軸焊接平衡塊示意圖

2.2 傳動軸當量夾角的分析與優化

2.2.1 傳動軸當量夾角計算

本文研究車型的傳動軸為多段式傳動軸結構如圖3所示，它由三個萬向節連接（三萬向節傳動軸如圖4所示，Ⅰ表示輸入軸，Ⅱ表示中間傳動軸，Ⅲ表示主傳動軸，Ⅳ表示輸出軸）。對本文研究車型傳動軸的當量夾角進行計算分析避免由于當量夾角過大導致轉速波動過大的問題。按照以往的經驗當量夾角θe必須小于3°。利用公式（2）對本文研究車型的當量夾角進行計算[3]。

圖3 傳動軸布置結構示意圖

圖4 三萬向節傳動軸示意圖

式中：θ1表示輸入軸與中間傳動軸軸線夾角（deg）；θ2表示中間傳動軸與主傳動軸軸線夾角（deg）；θ3表示中間傳動軸與主傳動軸軸線夾角（deg）；τ1表示順著傳動軸旋轉方向中間傳動軸與主傳動軸的軸線構成的平面與輸入軸和中間傳動軸軸線所構成的平面的夾角（超前為正，滯后為負）（deg）；τ2表示順著傳動軸旋轉方向輸出軸與主傳動軸的軸線所組成的平面與中間傳動軸和主傳動軸的軸線所構成平面的夾角（超前為正，滯后為負）（deg）；ψ1表示順著傳動軸旋轉方向中間傳動軸輸出端萬向節叉軸線與中間傳動軸輸入端萬向節叉軸線的夾角（超前為正，滯后為負）（deg）；ψ2順著傳動軸旋轉方向主傳動軸輸出端萬向節叉軸線相對與輸入端萬向節叉軸線的夾角（超前為正，滯后為負）（deg）。

本文所研究傳動軸參數如下：θ1=0.828 deg，θ2=4.298 deg，θ3=1.654 8 deg，τ1=-87.671 7 deg，τ2=-39.117 0 deg，ψ1=0 deg，ψ2=0 deg 代入公式（2）求得傳動軸的當量夾角θe=4.542 8 deg。本文計算的當量夾角已經超過了經驗值3 deg。這會造成傳動軸的振動過大，從而影響整車的NVH性能，所以必須對其進行硬點優化。

2.2.2 傳動軸當量夾角優化

從已知的傳動軸布置硬點計算得出θe=4.542 8°，數值大于設計要求3°，需要調節硬點將當量夾角θe降低。通過經驗分析，調整第二個萬向節點P3的X、Y和Z方向坐標值對傳動軸的當量夾角θe的影響較大，所以只須通過調節第二萬向節點P3基本就能找出最優的當量夾角θe。

將第二方向節點P3的坐標做成一個矩陣，X坐標點的變化范圍設置為±10 mm，每0.5 mm取一個數值，同理，Y坐標點的變化范圍設置為±5 mm，Z坐標點的變化范圍設置為±10 mm，每0.5 mm取一個數值；則P3的坐標點值形成了數組：

將P3數組逐個代入當量夾角θe計算公式中求出θe值最小時P3的硬點坐標。經過優化后的當量夾角θe=2.660 1 deg符合設計要求。利用UG運動仿真軟件計算傳動軸當量夾角優化前后的扭矩波動變化，如圖5所示可以看出優化后傳動軸的扭矩波動量降低了66.67%。證明對傳動軸當量夾角的優化對降低傳動軸的扭矩波動是有效的。

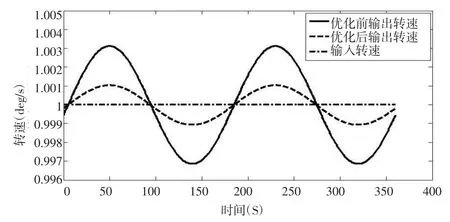
圖5 傳動軸轉速波動圖

2.3 臨界轉速計算

傳動軸一階旋轉頻率與傳動軸自身的彎曲模態一致時傳動軸發生共振破壞。這時候的轉速稱為臨界轉速。如果傳動軸在臨界轉速附近運轉，那么軸很可能斷裂，甚至破壞變速箱、驅動橋。所以設計傳動軸時候應該使其有足夠的臨界轉速。

式中：nk為傳動軸臨界轉速（r/min）；L為傳動軸長度（mm）；D 為傳動軸管的外徑（mm）；d為傳動軸管的內徑（mm）。

2.4 中間支撐對傳動軸振動的影響

用三個萬向節或四個萬向節將軸分段時，用中間支撐軸承來支撐傳動軸的中間部位。通常用球軸承來支撐軸，并通過橡膠等彈性體裝在車身或車架上如圖6及圖7所示。中間支撐的主要作用：補償傳動軸的安裝誤差和汽車運行中由于發動機的運動以及車架的變形而導致傳動軸的位移使其運動的時候可以自動尋找旋轉軸線，隔絕傳動軸產生的振動向車身傳遞。

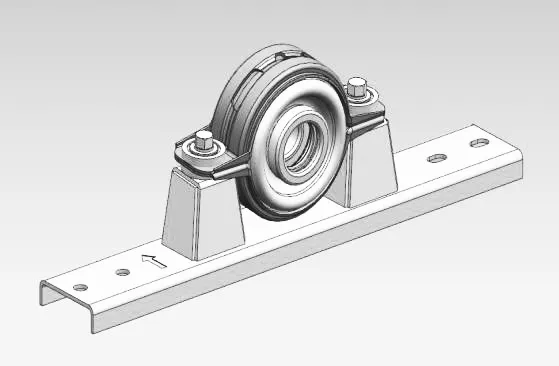
圖6 中間支撐結構示意圖

圖7 中間支撐安裝示意圖

根據系統隔振理論可知。激勵頻率ω和系統的固有頻率 ωn滿足 ω/ωn＞條件，隔振系統才真正起作用，要追求更好的隔振效果那就需要ω/ωn值越大[4]。但是由于中間支撐也起到限位的作用，因此它的剛度不可能設計得無限小這就導致了實際應用時ωn也不可取值過小，而造成傳動軸運動穩定性變差的問題。而且當ω/ωn上升到一定值后，振動傳遞率的減小趨于平緩，因此中間支撐頻率在一個合理的范圍內就能滿足要求。中間支撐的固有頻率可按下式計算[5]：

式中：f為中間支撐固有頻率（Hz）；c為中間支撐橡膠彈性元件的徑向剛度（N/mm）；m為中間支撐承受的質量（kg）。

本課題研究的車型的傳動軸中間支撐橡膠剛度c=24 N/mm，所承受的質量為m=2 kg,代入公式（4）算得f=17.43 Hz，為了使中間支撐有比較好的隔振效果需要中間支撐的固有頻率盡量避開發動機常用頻率。本文研究的車型的怠速為750 r/min，對應傳動軸的轉速為905.797 1 r/min，對應其二階振動頻率為30.19 Hz，由隔振理論支撐剛度符合隔振要求。

2.5 傳動軸的彎曲模態

傳動軸的彎曲模態頻率要求比軸工作范圍內的第一階振動頻率高10%，否則傳動軸的不平衡會引起整個軸系的振動。特別是對驅動橋旋轉軸的轉速比較高的情況，這種振動更容易產生。傳動軸一階振動頻率的計算公式如下：

式中：f為傳動軸的一階模態（Hz）；n為發動機的轉速（r/min）；i為變速箱傳動比。

本課題研究車型的發動機最高轉速n=6000r/min，變速箱五檔傳動比i=0.828代人公式（5）計算得到傳動軸一階振動頻率為120.8 Hz.所以傳動軸一階彎曲模態應該大于133 Hz。本文研究車型的傳動軸的彎曲模態由CAE分析計算值為204 Hz如圖8所示，傳動軸彎曲模態符合設計要求。

圖8 傳動軸一階彎曲振型

3 試驗驗證

通過對影響傳動軸振動因素進行了校核，對不符合設計要求的部分進行了優化使得傳動軸的振動明顯減小實測噪聲結果表明傳動軸的振動噪聲關鍵點位置噪聲值從63.28 dB變成了53.24 dB降低了10 dB如圖9所示，主觀感受傳動軸的振動明顯改善。

圖9 傳動軸振動噪聲試驗結果

4 結論

通過對故障車型的傳動軸進行優化分析及試驗驗證總結出解決傳動軸振動問題的方法：

（1）提高傳動軸殘余動不平衡量的精度等級到G16平衡品質等級對傳動軸的一階振動是有利的。

（2）控制傳動軸的當量夾角在3 deg以內可以減小傳動軸的扭矩波動可以改善傳動軸的振動問題。

（3）傳動軸在設計階段必須保證其臨界轉速符合設計要求以避免發生共振。

（4）用三個萬向節或四個萬向節將軸分段時，用中間支撐軸承來支撐傳動軸的中間部位，中間支撐的橡膠激勵頻率ω和系統的固有頻率ωn必須滿足ω/ωn＞條件，隔振系統才真正起作用。

（5）傳動軸的彎曲模態頻率要求比軸工作范圍內的第一階振動頻率高10%，否則傳動軸的不平衡會引起整個軸系的振動。