基于半正定測量的光量子OFDM通信系統在離散高斯噪聲環境下的性能分析

，

(復旦大學 信息科學與工程學院，上海 200433)

0 引言

量子通信是量子力學與通信技術相結合誕生的一個新興學科，是量子信息學的重要分支。基于量子力學原理，將微觀領域的物理特性加以分析并運用在通信技術上，量子通信具有傳統通信無可比擬的優勢，是當今世界通信領域的研究熱點[1]。然而，現有的量子通信系統通信速率較低，此類量子通信系統所需要的大量光纖資源是無法承受的。如果能在信道中同時傳輸多個不同波長的光脈沖，采用波分復用技術，就能夠很大程度的提升通信速率和信道容量。對于不同波長、頻率上獨立的光脈沖來說，正交頻分復用OFDM(Orthogonal Frequency Division Multiplexing)是契合度相當高的復用方式。目前，來自華中科技大學和電子科技大學的研究團隊分別實現了經典全光OFDM在光纖上的傳輸，分別為8路40 Gbits[2]和8路112 Gbits[3]。對于在全光OFDM系統中的量子態而言，大部分情況下都是非正交的，此時必須采用半正定算符測量POVM(Positive Operator Valued Measure)方法進行檢測，可以依據不同的準則設計相應的POVM算符對接收信號量子態進行測量。本文采用了平方根檢測SRM(Square Root Measurement)方法[4]，由信號量子態可以快速構造出用于檢測的POVM算符，具有較高的研究價值。同時，考慮到實際通信的要求，在接收端，由于量子熱噪聲的存在，接受態也會變為混合態。雖然高斯量子熱噪聲的引入會極大地增加問題復雜度，但通過對連續的高斯量子噪聲進行離散化近似，則可以在降低復雜度的同時盡可能的逼近實際情況[5]。

本文研究了量子通信的特點，基于馬赫岑德干涉儀MZI(Mach-Zehnder Interferometer)的光OFDM系統的通信、不同量子態相位調制對應的SRM檢測以及對量子高斯噪聲的離散化近似。第二部分介紹了基于MZI的光量子OFDM系統的實現過程。第三部分介紹了量子POVM檢測和量子SRM檢測方法以及該方法在量子OFDM系統接收端的應用。第四部分介紹了量子高斯噪聲對量子態的影響、離散化近似以及檢測問題。第五部分研究了基于SRM檢測的量子OFDM系統的性能，仿真了加入離散量子高斯噪聲后整體的檢測錯誤率并對其進行相應的分析說明。

1 基于MZI的量子OFDM系統

OFDM的主要思想是在頻域內將信道分成若干子信道，每個子信道上對一個子載波進行調制，各子載波并行傳輸。而基于MZI的OFDM系統可以全部在光域上實現，滿足量子通信的需求[6]。

在發送端，為保證各個子載波間的頻率間隔，由光頻梳生成器OCG(Optical Comb Generator)產生8個光子載波，彼此頻率間隔相等，在頻域上正交。然后利用MZI對于8個正交的光子載波進行量子態的調制。量子信號調制方式是基于MZI的相位調制方式。如圖1所示。

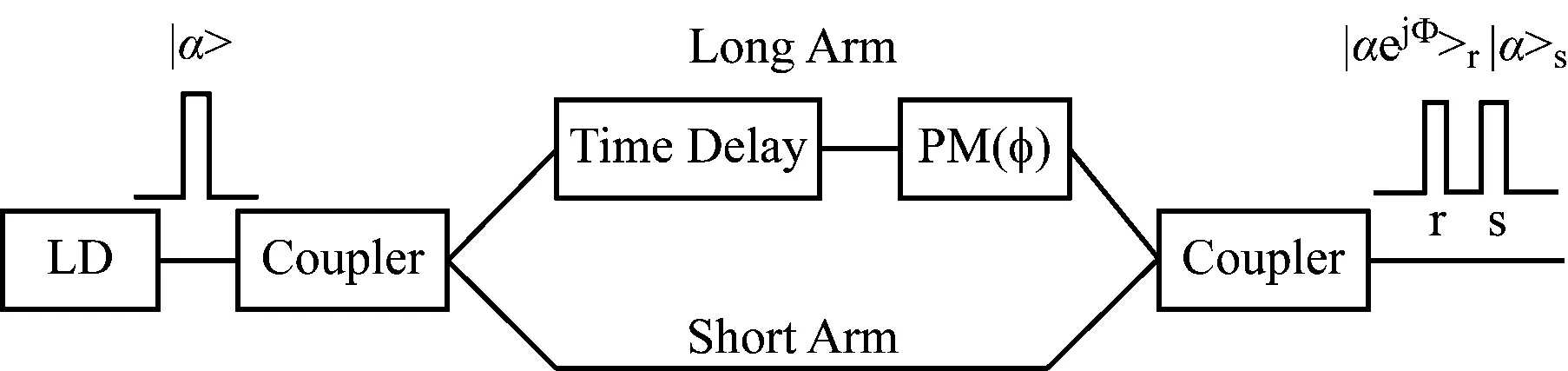
圖1 量子相位調制器

一個持續時間為T(T=1/Δf,其中Δf是子載波間隔)的光脈沖在發送方處被送入預先設定好相位差的MZI當中，輸出的結果是兩個持續時間同樣為T、非疊加的連續的脈沖，強度各為輸入脈沖的1/2，分別用r和s表示，這兩個光脈沖，他們之間的相位差Φ表征對應的經典信息，如圖2所示。

圖2 全光量子OFDM系統發射端示意圖

在對子載波調制完成后，通過光耦合器將n路光信號耦合為一路，產生攜帶光量子信息的OFDM符號。

在接收端，接收到的光量子OFDM信號通過一系列級聯的MZDI后對各路光子載波解復用，每個MZDI單元由2個耦合器、1個相移器和1段時延線組成。MZDI單元的延時與相移記為(τ,θ)，中心頻率為f，則其對應的傳輸函數可以記為式(1)。

(1)

光量子OFDM信號進入接收端后，每一級MZDI將對其進行延時和相移，經過3級MZDI延時后，光量子OFDM信號的8路光子載波被分離出來，如圖3所示。

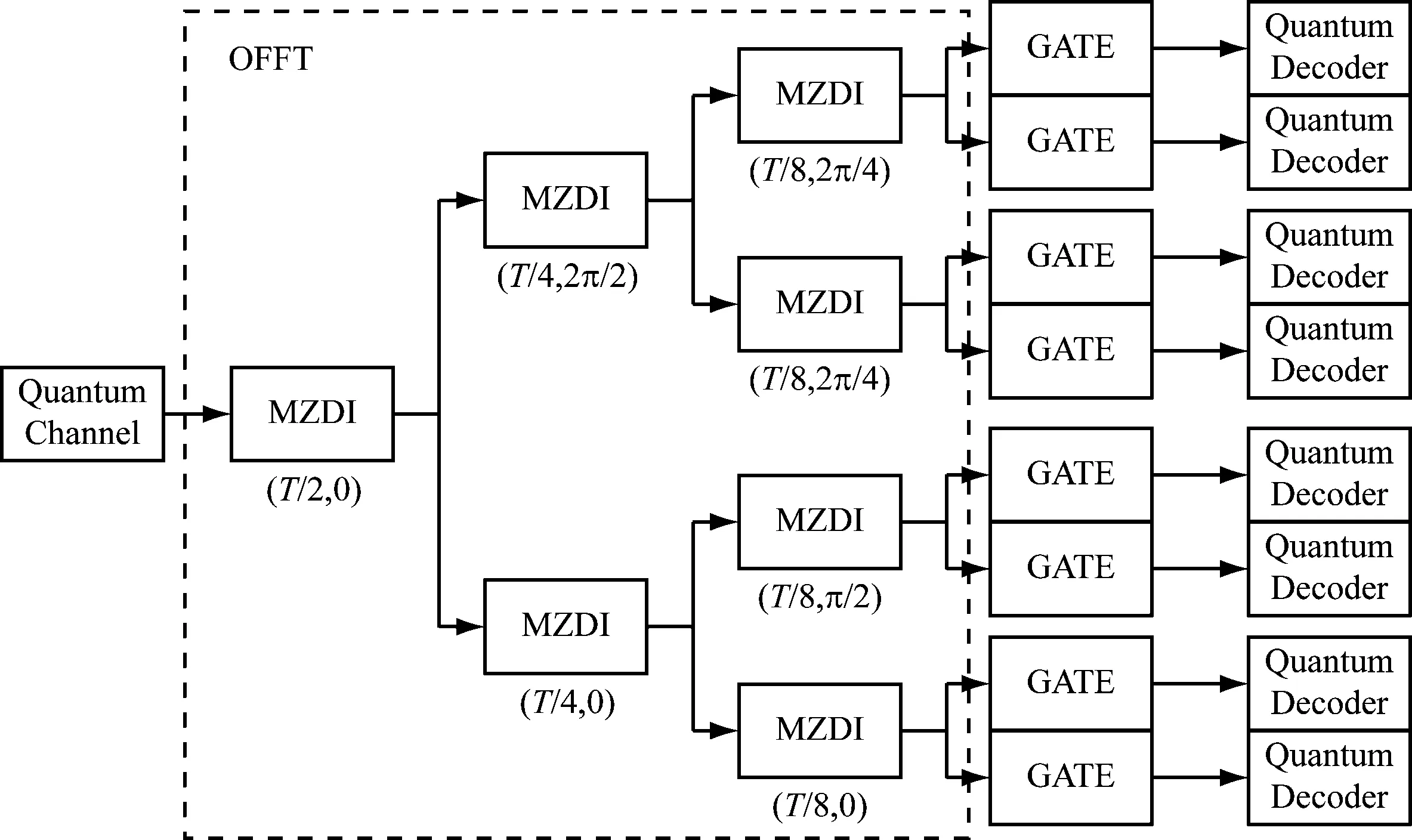
圖3 全光量子OFDM系統接收端示意圖(8路光脈沖子載波)

得到不同光子載波上的脈沖r和s后，使其通過預設好的MZI，通過檢測門得到相位差同為Φ的位于3個脈沖中間位置的光脈沖，輔以相應的檢測，從而得到量子信號當中的經典信息，如圖4所示。

圖4 量子相位解調器

由于信息調制是在兩個光脈沖相對相位上完成的，因此初始的光脈沖相位可以是任意的。同時，在系統傳輸的過程當中，由于采用了相對相位搭載信息，可能的相位影響會同時作用于兩個脈沖，并不會影響二者的相位差，使得系統對于相位噪聲有較強的抵抗能力。

2 量子相干態檢測

2.1 量子相干態

量子態有許多種形式，其中，相干態是指完全相干的量子光場，也是現實中最容易獲得的量子態。在光頻領域，電磁場借助于微觀粒子體系，通過經典源驅動，通過量子諧振產生相干態光場。因此，由激光器產生的激光就是相干態。相干態是非Hermitian算符的本征態，所以利用相干態集可以構成非正交、超完備的表象。而在光量子OFDM系統中，以QPSK經典信息向量子態的映射為例，可以直觀地看到，得到的相干態是非正交的，即式(2)。

k=1,3,5,7,m=1,3,5,7

(2)

顯然，當k≠m，即兩個相干態的本征值不同時，上式的值不等于0，即兩個相干態是非正交的。相干態的光子數態(Fock態)表象形式為式(3)。

(3)

2.2 最小平方根檢測

由于光量子OFDM系統中傳輸的量子態是相干態，而對應不同本征值的兩個不同的相干態是非正交的，因而不能通過諸如馮·諾依曼測量等基于完全正交的方法完全確定發送的量子態。因此，需要找到一組測量基，來最小化檢測非正交態的錯誤概率。量子平方根檢測是POVM檢測中效果較好的一種，是在最小平方根條件下的最優檢測。同時，也是當量子態集是由某種幾何對稱特性的量子態組成的系統中最優的方法。SRM方法的測量基構建十分簡潔，可以直接由給定的量子態集合得到。對發送的量子態集合{|αejφi〉}在光子數態表象下(維度為n)展開，得到集合{|φi〉}，它處于n維Hilbert空間中，向量|φi〉是線性獨立的，并由所有向量|φi〉構成矩陣Φ=[|φ1〉,…,|φn〉]，它是一個秩為r的n×K的矩陣。對矩陣Φ作奇異值分解，即Φ=U∑V*。記SRM測量矩陣為M，則有式(4)。

(4)

此時，對應的SRM測量是正交測量且滿足最優最小二乘測量準則。

取矩陣M的列向量，記為{|μi〉}，這就是最優的測量態集。針對SRM檢測方法，對于包含K個發射量子態的符號集系統，在輸入量子態等概率的條件下，檢測的誤碼率為[7]式(5)。

(5)

3 量子熱噪聲的引入

3.1 離散高斯噪聲模型

由于量子熱噪聲的引入，會使得接收端的量子態不再是純態而變為混合態，考慮對引入量子熱噪聲的相干態其進行近似。將積分轉換為無窮項和的形式表示，即將引入量子熱噪聲后的相干態視為一個有限數量的相干態的加權和，每個相干態出現的概率則有它所代表的區域Ajk的高斯權重決定。每一個特定的量子態對應復平面上一個特定的區域，接收到它的概率為Pjk是這片區域的權重。這一近似模型稱為“離散相干態”近似，即(DCS，discrete coherent state)。

由于高斯分布的性質，當距離更遠時，對應的權重會極大地減小，幾乎可以忽略不計。因此，以原始信號態為中心，一個單位處分布不同的疊加噪聲后的相干態足以相當準確地描述引入量子熱噪聲之后混合態的情況。

當發射的態為|φ0〉，接受態是[|φ00〉,|φ01〉,…,|φ0k〉],k=0,…,D-1中的任意一個，對應的概率為[P00,P01,…,P0k],k=0,…,D-1。這一系列可能相干態的概率分布則可以由高斯函數在對應區域內的權重得到，對于第k個發射態為式(6)。

(6)

在半徑為r圓上對上式積分，即可得到概率為式(7)。

P(r)k=1-e-(r2/N)

(7)

由于噪聲的引入，需要重新根據可能的接受態情況構造測量算符。任意一個可能的發射態都有了D個可能的接受態，故整個符號集由之前的K個變為K×D個。相對應的，對于混合態形式的接受態，其POVM算符變為式(8)。

(8)

信號矩陣Φ和測量矩陣M的尺寸均由n×K變為n×(KD)。

3.2 檢測錯誤率分析

上面已經提到，當接收量子態為純態，針對SRM檢測方法，對于包含K個發射量子態的符號集系統，在輸入量子態等概率的條件下，檢測的誤碼率由式(X)給出。而對于引入噪聲后的檢測，量子測量假設依舊適用。假設發射態為Hk，正確檢測的概率為式(9)。

(9)

對于包含K個發射量子態的符號集系統，記發射符號對應的先驗概率為P(Hk)，正確的檢測概率為式(10)。

(10)

由此易知，此時的檢測錯誤率為Pe=1-Pc。

4 系統仿真與分析

為了驗證本文中提到的光量子OFDM系統的性能，進行了相關的系統仿真。首先討論了對量子高斯近似后不同的離散量子態半徑范圍取值對實際復平面的覆蓋情況，然后仿真了引入不同強度的量子高斯噪聲對系統檢測性能的影響，最后，針對典型的不同的離散量子態半徑值在不同強度的量子高斯噪聲環境中的情況，進行了整體仿真，并就結果進行了相關討論。

在用離散相干態模型對引入的量子高斯熱噪聲進行近似時，近似量子態覆蓋區域的半徑r是一個較為重要的參數，對r分別取0.4，0.5以及0.6的情況時對整個復平面覆蓋比例的仿真結果,如圖5所示。

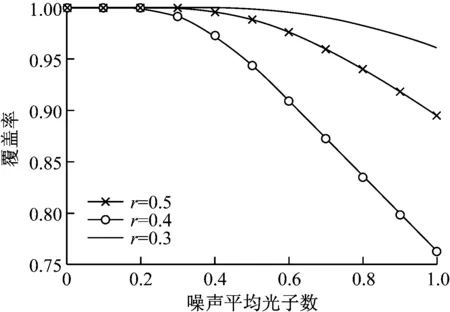
圖5 不同近似相干態覆蓋半徑覆蓋率隨噪聲平均光子數的變化

由仿真結果可以看到，在噪聲平均光子數較小，即量子高斯噪聲較小時，3種半徑取值均能很好的覆蓋整個復平面。這是因為，在噪聲較小時，疊加了噪聲的接受量子態只有很小的概率會出現在離發射的純態的位置較遠的地方。而隨著量子高斯噪聲的增大，疊加了噪聲的接受量子態出現在較遠位置處的概率不斷增大，此時較小的r覆蓋的區域就不能很好的大概率覆蓋可能的區域。

接下來我們仿真了在引入維度D=7，不同強度的量子高斯噪聲后對系統檢測性能的影響，結果如圖6所示。

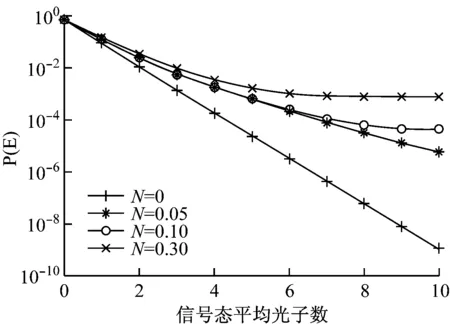
圖6 引入不同平均光子數高斯熱噪聲后系統性能(混合態維度D=5)

由仿真結果可以看到，在采用量子QPSK調制的系統中，對比N=0，即沒有任何量子高斯熱噪聲的情況，即使只引入平均光子數為0.05的量子熱噪聲，也會對系統的整體性能造成極大的影響。而隨著熱噪聲平均光子數的進一步增加，檢測的錯誤率也會進一步增大。注意到越是在信號態平均光子數較大的時候，有無噪聲的存在對系統的影響越大。這是一點可以理解的，因為在信號態平均光子數較大時，同樣的比例下疊加了噪聲的量子態會偏出更遠。

最后，為了綜合考慮前文中提到的因素，我們仿真了維度D=7情況下，兩種近似量子態覆蓋區域的半徑r對不同量子熱噪聲平均光子數的檢測性能，如圖7所示。

由仿真結果可以看到，在覆蓋區域半徑r相同的情況下，較小的噪聲平均光子數N對應的檢測錯誤率更低，與圖7所得的結論相一致。而在其他參數都相同的情況下，較小的量子態覆蓋區域的半徑的檢測正確率更低，因為它對噪聲引入的區域覆蓋的比例更低，這是可以理解的。但同時也應該意識到，這里的r也并不是取的越大越好，因為當r取的太大，實際上是將很大范圍內疊加了噪聲的混合態都作為純態處理，這樣也就失去了討論引入量子熱噪聲的實際意義。

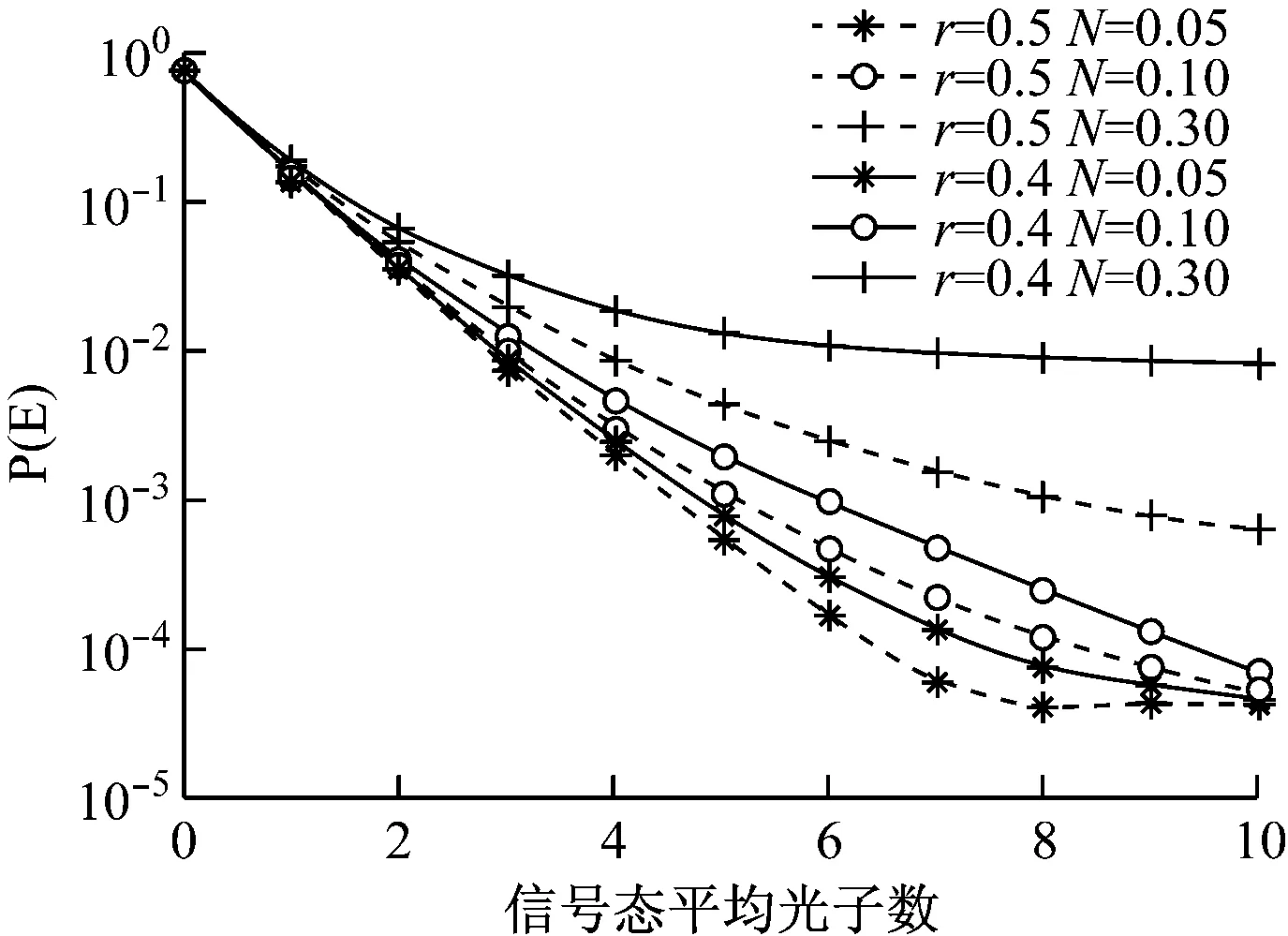
圖7 不同近似相干態覆蓋半徑下量子高斯熱噪聲對系統的性能影響(混合態維度D=7)

5 總結

本文研究了量子通信的原理特點以及基于馬赫岑德干涉儀的全光OFDM系統，結合量子相位調制的方法，研究并分析了基于馬赫岑德干涉儀的光量子相位調制OFDM通信系統。針對光量子OFDM相位調制發送量子態符號集不正交的特點，將發送量子態符號集在光子數態表象下展開，并采用了最小平方根的量子測量方法。并且引入離散量子高斯熱噪聲近似這一噪聲模型，并通過仿真討論了量子熱噪聲的引入及諸如混合態維度、近似范圍、噪聲平均光子數等不同噪聲參數對系統所造成的影響及原因。