基于換電運營模式的電動車電池充電策略研究

， ， ，

(同濟大學 電子與信息工程學院,上海 201804)

0 引言

隨著能源短缺日益嚴重，環保呼聲高漲，電動汽車(electric vehicle, EV)作為一種低碳、情節的交通工具，受到世界各國政府的高度關注[1]，成為我國新時期重點發展的7個戰略性新興產業之一[2]。電池是電動汽車運行的能量來源。規模化電動汽車運行以后，必將帶來蓄電池的充電問題[3]。本文通過蒙特卡洛方法模擬出電動汽車的出行分布特征和換電需求分布特征，并由此使用線性規劃算法求解運營成本最低的充電方案。

換電模式是一種基于換電站(Battery Swap Station, BSS)的充電模式，換電技術最初是由Renault和Better Place公司提出的，目前成為電動汽車產業發展的新模式。在這種模式下，用戶只需要在一個距離最近的換電站或配送站，用他們需要充電的電池換取已充滿的電池即可。由于換電式電動汽車在出行距離和能源交換方式方面的優勢，基于換電模式的充電策略已經提出，并且在近幾年受到了越來越多的關注[4]。

本文利用真實的私家車出行數據，通過蒙特卡洛方法模擬出大規模電動汽車在一天內的出行分布和換電需求分布，再基于這些模型建立了換電站的運營成本模型，包括了電池充電成本、儲備電池成本和充換電設備成本。在此基礎上，利用線性規劃算法求出最優的電池充電調度策略。

1 基于蒙特卡洛方法的電動汽車換電需求分析

蒙特卡洛方法[5]的基本思想是當所求解的問題是某種隨機時間出現的概率，或者是某個隨機變量的期望值時，通過某種“隨機試驗”的方法，以這種事件出現的頻率估計這一隨機事件的概率，或者得到這個變量的某些數字特征，并將其作為問題的解。由于電動汽車的換電服務仍是一個正在規劃的行業，目前沒有確切的換電服務需求模型，因此，本文查閱了小汽車出行分布模型，通過蒙特卡洛方法模擬每輛電動汽車在一個統計周期內的出行分布和剩余電量分布，從而得到電動汽車換電服務需求模型。

文獻[6]統計了北京市居民小汽車的出行時間分布，通過統計可以發現，小汽車的日均出行次數為3.16次/日。考慮到每天的差異性，對于N輛電動汽車，可以假設每天出行的總數量服從U[3N,3.32N]的均勻分布。本文依據北京市居民小汽車的出行時間分布和出行比例作為電動汽車的出行比例，在一小時內按照均勻分布,如圖1所示。

圖1 私家車出行比例

文獻[7]按照不同的城市規模和城市布局建立了私家車出行距離分布模型，發現城市私家車每次出行的距離服從瑞利(Rayleigh)分布，并且由于城市規模與布局的不同，瑞利分布的參數λ也不同，對于上海這種大型城市而言，可選λ=11.17。

假設電池容量為19.2 kWh，從滿電到空電行駛100 km。電動汽車的行駛行為是其主要的耗電原因，因此若要建立電動汽車換電的日需求模型，必須描述車輛在一天內的行駛狀況。考慮到車速不斷變化會對行駛距離造成影響，進而影響到電池電量消耗的過程，可假設電動汽車在行駛過程中每個時刻的時速S滿足正態分布，本章的每個時刻表示1分鐘的時長，可認為車輛速度在1分鐘內是恒定的。S服從N[21,32]的正態分布。

本文以換電閾值作為判斷電動汽車是否前往換電站進行換電服務的依據，換電閾值分為兩類：一類是車輛在剩余電量過低時，為了維持車輛良好的使用狀態所產生的換電需求，以QL表示其換電閾值，稱為低電量閾值，該類型需求為低電量換電需求；另一類時電動汽車在一天最后一次出行結束后，為次日進行電能儲備而產生換電需求，以QS表示其換電閾值，稱為儲備閾值，該類型需求為儲備換電需求。依據QS的定義，可以認為QL小于等于QS，并且認為電動汽車在計算初始時刻的電量與儲備閾值有關。假設QS=[0.35,0.55],QL=[0.10,0.20]]，電動汽車在日常行駛中，會在電量位于QS范圍內時隨機前往換電站進行換電，當電動汽車在進行一天內的最后一次行駛活動時，若結束時的電量位于QL范圍內，則電動汽車有可能在最后一次行駛的全過程內接受一次換電服務，進行換電服務的時間滿足均勻分布。

上海市目前常住人口為2 415萬，其中嘉定區常住人口為143萬人，至2017年上海市私家車保有量為213萬輛，取電動汽車滲透率為5%，可算出嘉定區電動汽車數量為6 330輛，本文將這6 330輛電動汽車作為換電服務的研究對象。

考慮到車輛的運行規律，部分車輛的運行可能會持續到24:00之后，且車輛每天第一次出行時的電池電量不一定滿足均勻分布。為了減小對分析結果的影響，所有計算均以2:00作為開始的時刻，連續進行兩天的計算，并將第二天的結果作為最終的模擬結果。通過蒙特卡洛方法得到的電動汽車換電的時間分布模型,如圖2所示。

圖2 電動汽車的日換電需求分布

經過一天的運行，6 330輛電動汽車會產生2 353次換電需求，如何對這些換電需求進行優化，從而減少換電站的運營成本是本文研究的核心。

2 電動汽車換電站的運營成本分析

電動汽車換電的成本模型可以分為3部分，電池充電成本，儲備電池成本和充換電設備成本。

(1) 電池充電成本

在此使用兩部制電價進行充電成本模型的建立，充電成本分為電量電價成本和基本電價成本，分別與實際充電電量與最大充電功率相關，電價使用上海市商業分時電價，具體參數如表1所示。

表1 分時電價與最大需求參數

充電成本的公式為式(1)。

(1)

式中:

Ccharge表示充電成本；

∑t∈T(C(t)×E(t)×P)表示電量電價；

C(t)表示在t時刻充電的電池數量；

E(t)表示t時刻的電價，P表示電池充電功率；

kmax_demand表示最大需量參數。

(2) 儲備電池成本

采用換電模式進行能量更換，電動汽車更換下的電池由集中式充電站安排充電，待充滿后電池會在下一個時刻運至電池配送站等待電動汽車取用，并在為電動汽車更換電池時獲得其他待充電電池。電池循環示意圖如圖3所示。

圖3 電池循環示意圖

將模型中充電站所保有的電池都視作站內儲備庫電池，根據電池循環流程圖可知，儲備庫電池分為滿電待用電池、正在充電電池和待充電電池，分別用兩個集合BF,BC和BN分別表示，可知換電站的儲備電池總數為|BT|=|BF|+|BC|+|BN|。

對于時刻t而言，對于BN,BC和BF而言分別存在約束條件，如式(2)。

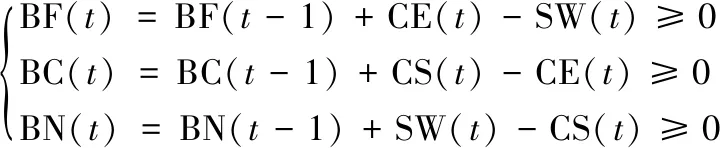
(2)

式中:

BF(t),BC(t),BN(t)分別表示t時刻滿電待用電池、正在充電電池和待充電電池的數量；

SW(t)表示t時刻更換下的待充電池數量；

CS(t)表示t時刻開始充電的電池數量，只要滿足上述約束條件即為儲備電池的可行解，儲備電池成本正比于最少儲備電池的數量；

CE(t)表示t時刻結束充電的電池數量。

儲備電池成本的計算式為式(3)。

Cbattery=|BT|×kbattery

(3)

式中，kbattery為折算后每塊電池每日的折舊成本。

(3) 充電設備成本

充電設備成本為換電站為充電準備的電池充電機的成本，該成本正比與充電策略中的最大同時充電電池數。其計算式為式(4)。

(4)

式中，kche為折算后的單臺充電設備每日運營成本。

3 換電站內電池充電策略的優化方法分析

換電站對電池充電策略相關的運營成本主要包括了電池充電成本，儲備電池成本和充電設備成本。

假設充電機的功率為5 kW，電池功率為19.2 kWh，充電策略將一天劃分為每段4小時的6個時段，分別2:00-6:00, 6:00-10:00,10:00-14:00,14:00-18:00,18:00-22:00,22:00-次日2:00。在每個時段開始時將電池統一接入充電裝置，在每個時段結束時將已充滿的電池統一從充電裝置中移除，故每個時段的充電電池數量即為該時段開始時進行充電的電池數量，每個時段獲得的新充滿待用電池數量為上一時段開始充電的電池數量，如式(5)。

(5)

6個時間段的電價向量e=[0.291 0,0.291 0,1.005 5,1.005 5,0.892 3,1.118 8]kWh。通過換電模型可知一天內更換的電池總量為2 353塊，平均每塊電池需要充電12.33 kWh。假設充電策略為c=[c1,c2,c3,c4,c5,c6]，則電量電價成本為e×c，基本電價為40.5/30×5×max(c)，充電設備運營成本為0.72×max(c)。

可以看出，構建的運營成本模型主要存在兩個非線性因素：充電設備成本計算過程中的電池最大充電數量max(c)和儲備電池成本的迭代計算過程。在使用算法對系統進行優化前，需要首先消除這兩項非線性因素。

對于非線性變量max(c)，通過對充電成本的定性研究可以發現，充電最多的時刻一定位于電價最低的時刻，即max(c)=max(c1,c2)，由于c1和c2為換電服務的低谷時間段，在這段時間內充滿電池的數量高于換電服務需求的電池數量，故c1和c2的選擇只影響充電設備成本，而不會影響充電成本和儲備電池成本。因此，最優的充電策略會讓c1和c2的值相等，且為向量c=[c1,c2,c3,c4,c5,c6]的最大元素，故可令c1=c2,max(c)=c1。

對于儲備電池成本而言，消除非線性因素的方法是假設[bf,bc,bn]為一天開始時換電供應商擁有的滿電待用電池、正在充電電池和待充電電池數量。將[bf,bc,bn]作為待求變量放入充電規劃模型中，即將規劃的解由c=[c1,c2,c3,c4,c5,c6]擴充為c=[c1,c2,c3,c4,c5,c6,bf,bc,bn]。

此時還需對式(2)的約束做線性化操作。

對BC和BT的線性化操作類似于BF，在此不做過多描述。

因此，充電策略的規劃模型為式(6)。

式中，

(6)

4 算例分析

配送站和換電站中的儲備電池，充電設備和換電設備具有不同的使用成本和使用壽命。對各類資源的單價及維護費用按表2進行設置。

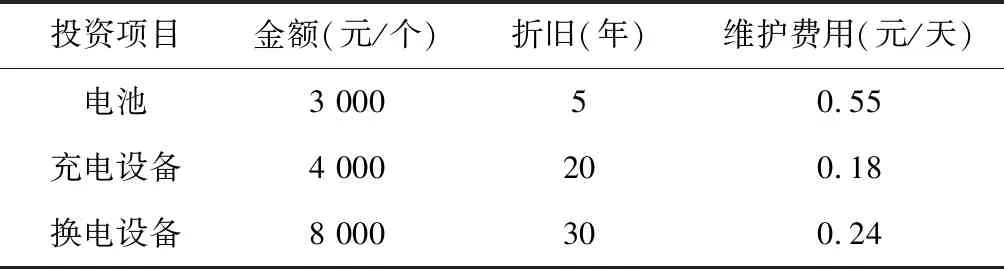
表2 設備單價及維護費參數

4.1 未進行充電策略優化的成本分析

通過蒙特卡洛方法模擬出的換電分布模型(圖2)作為研究對象，在沒有任何優化策略的條件下，可計算電動汽車換電服務商每天的運營成本。

a) 充電成本

由于電池總電量為19.2 kWh，假設充電功率為5 kW，則認為單塊電池的充電周期為4小時，因此可將一天分成6個充電周期，每個周期內充電站將上個充電周期內更換下的待充電池充滿，并將已充滿的電池配送至配送站。充電站在6個充電周期內充的電池數量,如圖4所示。

在這樣的充電分布下，充電站每日的電量電價成本為27 682元/天，折算的基礎電價為7 924元。

b) 儲備電池成本

儲備電池的數量與充電分布和換電分布均相關，在沒有任何優化措施的條件下，每個充電周期會將上個周期更換的待充電池充滿，并將這些電池在下個充電周期開始時配送至各配送站。通過24小時的迭代計算可求出儲備電池數量為1 859塊，各個充電周期內的已充滿電池和未充滿電池如圖5所示。由表2得kbattery=2.19，可計算出儲備電池成本為4 071元。

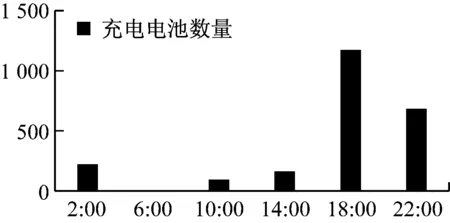
圖4 即換即充策略下的充電電池分布

c) 充電設備成本

綜上所述，在沒有任何優化策略時，換電站每日運營總成本為40 522元。如圖5所示。

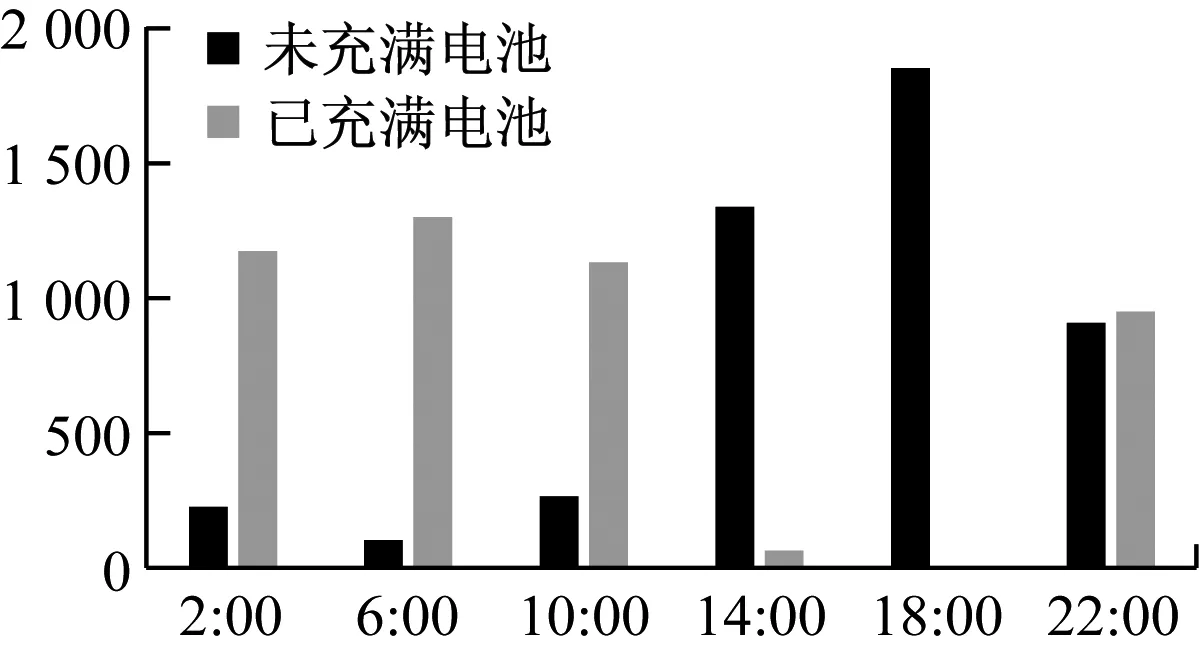
圖5 充電站已充滿電池與未充滿電池分布

4.2 進行充電策略優化的成本分析

對以上模型進行線性規劃，可求得最優解為c=[1 177,0,0,0,0,1 176]，可以看出此時充電策略(如圖6)會偏向電價較低的時間段進行充電。此時的儲備電池數量為2 348塊，換電站內3種類型的電池分布如圖6所示。

圖6 優化充電策略后充電站充電策略

使用優化充電策略后，可得換電商各部分成本為：

電量電價成本：8 448元;

基本電價成本：7 938元;

充電設備成本：847元;

儲備電池成本：5 142元。

綜上，使用充電策略優化后，換電商和充電相關的運營總成本為24 175元。使用充電策略優化后的各項運營成本與未進行充電策略優化前的各項運營成本對比如表3所示。

由表3可得，在建立的換電服務商的運營成本模型中，相比即換即充的充電策略，使用優化后的充電策略能通過減少充電成本和儲備電池的成本，減少約40%的運營成本。如圖7所示。

表3 充電策略優化前后的換電站運營成本分析

圖7 優化充電策略后充電站各類電池分布情況

5 總結

本文主要通過蒙特卡洛方法模擬出換電式電動汽車在一天內的出行分布特征和換電需求分布特征，并建立了換電運營商的運營成本模型。同時，本文建立了換電運營成本與電池充電策略之間的關系模型，并將其規約為一個線性規劃求解最優值的問題。最后，本文使用了整數線性規劃算法對充電策略進行求解，并與未進行優化前的成本進行比較和分析。可以看出，在使用的算例中，用充電策略優化后，換電運營商的成本相比未使用充電策略優化前減少了約40%。