轉盤上物塊摩擦力的分析及變式訓練

廣東 古煥標

轉盤模型問題是高中物理中學習“向心力”后的習題內容，是對摩擦力概念的深入理解，也是高考常考內容之一。按照轉盤所處的平面和物塊有無細繩牽連，轉盤模型可分為水平轉盤物體無繩牽連、傾斜轉盤物體無繩牽連、單物體有繩牽連、多物體同側或異側有繩牽連等。解決轉盤模型問題時，不少學生由于對靜摩擦力大小和方向的不確定性把握不準，對不同條件下物塊的受力分析存在較大困難，為此本文從教材入手，通過舉一反三的變式訓練讓學生掌握此類模型的解題方法。

一、回歸教材─問題源于課本

【教材】問題與練習(人教版物理·必修2，P25)

【題目】一個圓盤在水平面內勻速轉動，角速度是 4 rad/s。盤面上距圓盤中心0.10 m的位置有一個質量為0.10 kg的小物體在隨圓盤一起做勻速圓周運動，如 圖5.6 - 7。

(1)求小物體所受向心力的大小。

(2)關于小物體所受的向心力，甲、乙兩人有不同意見：甲認為這個向心力等于圓盤對小物體的靜摩擦力，指向圓心；乙認為小物體有向前運動的趨勢，靜摩擦力方向和相對運動趨勢方向相反，即向后，而不是與運動方向垂直，因此向心力不可能是靜摩擦力。你的意見是什么？說明理由。

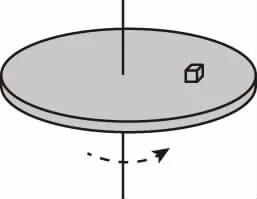
圖5.6 - 7 求盤上小物體隨盤做勻速圓周運動的向心力

【解析】(1)根據牛頓第二定律得

F=mω2r=0.1×42×0.1 N=0.16 N

(2)甲的意見是正確的。

靜摩擦力的方向與物體相對接觸面運動的趨勢方向相反。小物體在隨轉盤勻速轉動的過程中，相對轉盤有沿半徑向外運動的趨勢。

【感悟】本題的目的是讓學生綜合分析做勻速圓周運動的物體所受的靜摩擦力和運動之間的關系。

二、變式訓練─問題舉一反三

1.水平轉盤物體無繩牽連

【解題策略】物體隨水平方向上的轉盤轉動時，物體與轉盤間無繩牽連的情況，物體做圓周運動所需的向心力由轉盤對物體的靜摩擦力來提供，若F需≤F摩m，物體做圓周運動；若F需>F摩m，由于物體無繩牽連，物體將做離心運動。

【變式1】如圖1所示，兩個質量均為m的小木塊a和b(可視為質點)放在水平圓盤上，a與轉軸OO′的距離為l，b與轉軸的距離為2l。木塊與圓盤的最大靜摩擦力為木塊所受重力的k倍，重力加速度大小為g。若圓盤從靜止開始繞轉軸緩慢地加速轉動，用ω表示圓盤轉動的角速度。下列說法正確的是

( )

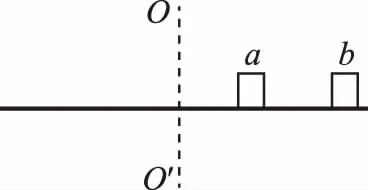
圖1

A.b一定比a先開始滑動

B.a、b所受的摩擦力始終相等

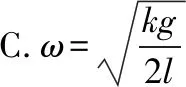
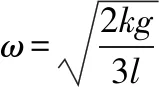
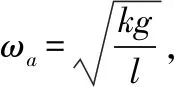
【答案】AC

【感悟】本題中小木塊a、b隨著圓盤一起做圓周運動的向心力來自圓盤對小木塊a、b的靜摩擦力，隨著轉速的增加，靜摩擦力逐漸增大。解決本題的關鍵是分析小木塊a、b所受的靜摩擦力誰先達到最大靜摩擦力，最大靜摩擦力對判斷物體的臨界狀態起著關鍵性的作用。

2.傾斜轉盤物體無繩牽連

【解題策略】物體隨傾斜轉盤轉動時，物體與轉盤間無繩牽連的情況，物體轉到傾斜轉盤上的最高點或最低點做圓周運動所需的向心力由物體本身的重力沿斜面方向的分力和轉盤對物體的靜摩擦力來提供，若F需≤F摩m，物體做圓周運動；若F需>F摩m，由于物體無繩牽連，物體將做離心運動。

( )

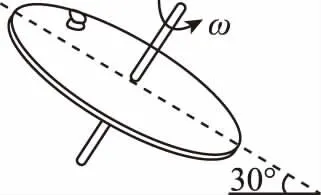
圖2

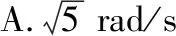
C.1.0 rad/s D.0.5 rad/s

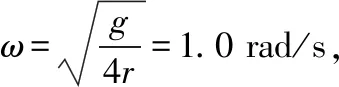
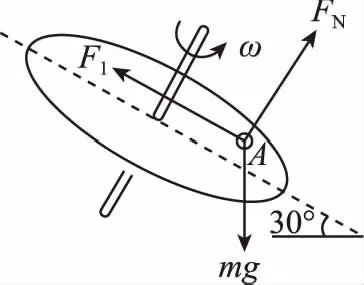
圖3

【答案】C

【感悟】解答本題的關鍵是要分析小物體轉到傾斜圓盤上最高點時和最低點時的受力情況，只要小物體轉到最低點時不發生相對滑動就能始終不發生相對滑動，當小物體轉到圓盤的最低點恰好不滑動時所需的向心力由物體本身的重力沿斜面方向的分力和轉盤對物體的最大靜摩擦力來提供。

3.單物體有繩牽連

【解題策略】物體隨轉盤轉動時，物體與轉盤間有繩牽連的情況，物體做圓周運動所需的向心力要注意臨界問題，若F需≤F摩m，繩子無張力，物體做圓周運動；若F需>F摩m，由于物體與轉盤間的最大靜摩擦力不足以提供物體做圓周運動所需的向心力，繩子此時有張力，物體做圓周運動所需的向心力由最大靜摩擦力和繩子張力的合力來提供。

【變式3】如圖4所示，水平轉盤上放有質量為m的物體(可視為質點)，連接物體和轉軸的繩子長為r，物體與轉盤間的最大靜摩擦力是其壓力的μ倍，轉盤的角速度由零逐漸增大，求：

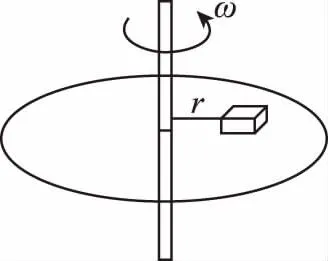
圖4

(1)繩子對物體的拉力為零時的最大角速度；

【解析】(1)當恰由最大靜摩擦力提供向心力時，繩子拉力為零且轉速達到最大，設轉盤轉動的角速度為ω0，則：

μmg=mω02r

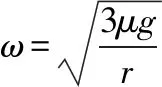
F+μmg=mω2r

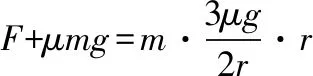
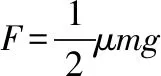
【感悟】本題涉及物體有細繩牽連，解決此類問題的關鍵是要考慮達到臨界條件時物體所處的狀態，只有當物體所受的靜摩擦力達到了最大靜摩擦力后，再增大轉速，拴住物體的細線才有張力作用，分析該狀態下物體的受力特點，結合圓周運動知識，列出相應的動力學方程綜合求解。

4.多物體同側有繩牽連

【解題策略】兩個物體與轉盤間有繩牽連、同側放置的情況，物體做圓周運動所需的向心力要注意臨界問題，分析各個物體的受力特點，若兩個物體所需的向心力都小于或等于最大靜摩擦力，即F需≤F摩m，此時繩子無張力，物體做圓周運動；若其中一個物體所需的向心力大于最大靜摩擦力，即F需>F摩m，此時繩子有張力，物體靠細線的張力與圓盤的靜摩擦力的合力提供向心力做勻速圓周運動，列出相應的動力學方程來求解。

【變式4】如圖5所示，一圓轉盤可在水平面內勻速轉動，沿半徑方向有兩個物體用輕繩連接，兩物體質量相等，且與轉盤間的動摩擦因數相同，當圓盤轉速加快到兩物體剛好還未發生滑動時，某一時刻剪斷繩子，則兩物體的運動情況是

( )

A.兩物體均沿切線方向滑出轉盤

B.兩物體均沿半徑方向滑出轉盤

C.兩物體仍隨轉盤一起做勻速圓周運動，不會發生滑動

D.A仍隨轉盤一起做勻速圓周運動，B發生滑動

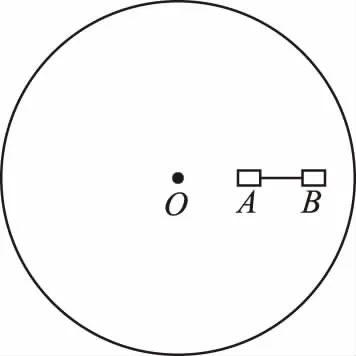
圖5

【解析】當圓盤轉速加快到兩物體剛要發生滑動時，B物體靠細線的拉力與圓盤的最大靜摩擦力的合力提供向心力做勻速圓周運動，A靠指向圓心的靜摩擦力和拉力的合力提供向心力，所以剪斷細線后，B所受最大靜摩擦力不足以提供其做圓周運動所需要的向心力，B要發生相對滑動，離圓盤圓心越來越遠，但是A所需要的向心力小于它的最大靜摩擦力，所以A仍保持相對圓盤靜止狀態，做勻速圓周運動.故D正確，A、B、C錯誤。

【答案】D

【感悟】本題中要關注臨界狀態，即靜摩擦力達到最大值后，繩子才開始有張力。解決本題的關鍵是對A、B兩個物體進行受力分析，找出向心力的來源，知道A、B兩物體是由摩擦力和繩子的拉力提供向心力。

5.多物體異側有繩牽連

【解題策略】兩個物體與轉盤間有繩牽連、異側放置的情況，物體做圓周運動所需的向心力要注意臨界問題和靜摩擦力方向發生改變的問題，分析各個物體隨轉速增大的動態受力特點，若兩個物體所需的向心力都小于或等于最大靜摩擦力，即F需≤F摩m，此時繩子無張力，物體做圓周運動；若其中一個物體所需的向心力大于最大靜摩擦力，即F需>F摩m，此時繩子有張力，而且隨著轉盤轉速的增大，靜摩擦力的方向可能會發生改變，物體靠細線的張力與圓盤的靜摩擦力的合力提供向心力做勻速圓周運動，列出相應的動力學方程來求解。

【變式5】如圖6所示，在勻速轉動的水平圓盤上，沿半徑方向放著用細線相連的質量均為A和B，它們分居圓心兩側，與圓心距離分別為RA=r,RB=2r，與圓盤間的動摩擦因數μ相同，當圓盤轉速加快到兩物體剛好還未發生滑動時，最大靜摩擦力等于滑動摩擦力，下列說法正確的是

( )

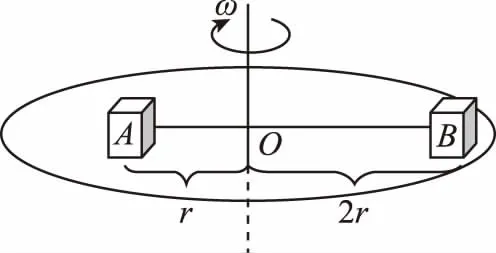
圖6

A.此時繩子張力為3μmg

C.此時A所受摩擦力方向沿半徑指向圓外

D.此時燒斷繩子，A仍相對圓盤靜止，B將做離心運動

【解析】兩物體剛好未發生滑動時，A受背離圓心的靜摩擦力，B受指向圓心的靜摩擦力，其大小均為μmg，則有：

FT-μmg=mω2r

FT+μmg=mω2·2r

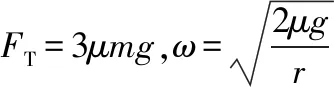
故選項A、B、C正確；

當燒斷繩子時，A所需向心力為：

F=mω2r=2μmg>Ffm

所以A將發生滑動，選項D錯誤。

【答案】ABC

【感悟】本題注意分析物體A和B所受靜摩擦力的大小和方向隨圓盤轉速的變化而發生變化，解決本題的關鍵是要知道角速度達到最大時，A和B的靜摩擦力都達到最大靜摩擦力，但方向相反，分析向心力來源，運用牛頓第二定律求解。