建模例析天體漂浮瓦解問題——2018年全國Ⅱ卷一道天體問題給物理教學帶來的啟示

遼寧 姜宗祎

2018年全國Ⅱ卷第16題是一道天體物理問題，主要考查萬有引力定律的理解和運算，但是許多學生反映解題時存在諸多疑惑。下面筆者結合教學實踐，具體闡述在天體漂浮瓦解問題的教學中，如何突破教學難點的實踐經歷。

1.建構地球表面物體萬有引力、重力、向心力關系模型

解決天體漂浮瓦解問題，首先應該弄清楚萬有引力到底等于什么(充當什么力)？重力與萬有引力有何關系？一般只有如下兩種情況：

(1)地球上的物體(忽略地球自轉影響)，一般來說F萬=G。

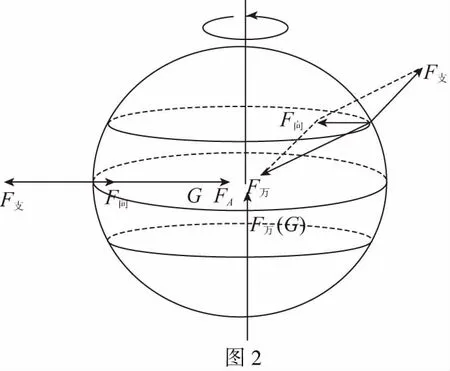
注意上式中是矢量的運算，滿足平行四邊形法則，如圖1所示。萬有引力是原始力，提供了兩個效果，一個是讓物體圍繞地軸旋轉，另外一個是使物體壓緊地球。此時也可等效理解為將萬有引力進行分解，其中一個分力指向地軸，提供物體所需的向心力，另外一個分力與支持力相平衡，這個分力就是重力。這里的重力其實就是在地面上用平衡稱量法測出的重力。

在兩極，物體沒有自轉效果，故向心力為零，萬有引力等于重力，均指向地心。在赤道，萬有引力、重力、向心力共線，重力過地心，這個時候自轉效果最明顯，所以物體的向心力最大，不過依然只有萬有引力的0.3%。 因此，忽略地球自轉可認為地球表面的萬有引力等于重力。

我們還可以從另外一個角度理解，以地心為參考系，物體做繞地軸上某點的勻速圓周運動，故物體受萬有引力和支持力，二者的合力提供物體所需的向心力，如圖2所示。

2.根據物理模型，設計物理問題，促進物理規律的融合

對于天體漂浮瓦解問題，難點在于學生對重力與萬有引力關系分析不清，向心力來源分析不清。因此，我們要通過一些問題的訓練，讓學生體會物理情境與物理規律的融合。

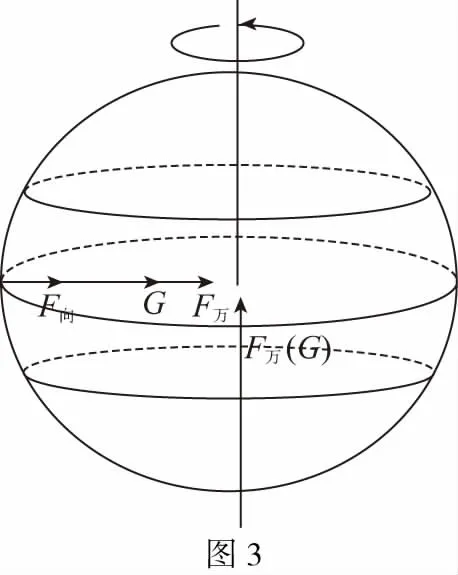
問題1：天空中有一顆繞恒星做勻速圓周運動的行星，此行星上一晝夜的時間為T，在行星的赤道處用彈簧測力計測量物體的重力讀數比在兩極時測量的讀數小10%，已知萬有引力常量為G,求此行星的平均密度。

試題分析：根據題意,赤道物體做勻速圓周運動所需向心力為萬有引力與重力之差,兩極位置重力等于萬有引力。如圖3所示，設行星半徑為R,質量為M，物體質量為m(視為質點)

在赤道上，F萬-G物=F向

根據牛頓第二定律列方程得

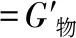
根據萬有引力定律列方程得

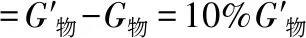
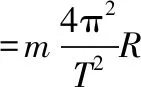
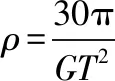
問題2：在問題1中，若在赤道處用彈簧測力計測量物體的重力讀數比在兩極時測量的讀數小9%，設想該行星自轉速度加快，在其赤道上的物體會自動“漂浮”起來，求這時該行星自轉周期。

試題分析：由題意可知,赤道表面物體做勻速圓周運動，所需向心力為萬有引力與重力之差，在地面上靜止的物體，物體對地面壓力數值上等于物體所受重力。若星球的自轉角速度越大、則周期越小,需要的向心力越大,物體對地面壓力越小，當周期達到某一最小值時,物體對星球表面應剛好沒有壓力,物體會離開星球表面，即赤道表面上的物體所受萬有引力恰好充當物體做勻速圓周運動所需的向心力。故赤道上物體“漂浮”即萬有引力全部充當向心力，根據牛頓第二定律列方程得：

再根據赤道兩極萬有引力和重力關系易知，在赤道上物體將其9%的萬有引力提供向心力，根據牛頓第二定律列方程得：

由以上兩式聯立得T0=0.3 T

問題3：(2018全國Ⅱ卷第16題)2018年2月，我國500 m口徑射電望遠鏡(天眼)發現毫秒脈沖星“J0318+0253”，其自轉周期T=5.19 ms，假設星體為質量均勻分布的球體，已知萬有引力常量為6.67×10-11N·m2/kg2。以周期T穩定自轉的星體的密度最小值約為

( )

A．5×109kg/m3

B．5×1012kg/m3

C．5×1015kg/m3

D．5×1018kg/m3

【試題分析】題干給出自轉周期T,引力常量G，要求星體穩定自轉，求最小密度。這道題看似簡單，其實不然。“最小”“穩定”四字涉及重力、萬有引力和向心力的深入考查。進一步分析可以得出“最小”“穩定”這兩個關鍵詞背后的隱含條件，即星體穩定運行，臨界狀態是其赤道上物體隨星體一起自轉不瓦解，也就是星球內部對其赤道表面物體的萬有引力恰好提供其所需向心力。當然萬有引力也可以比向心力大，所以星體密度有最小值。假設赤道上隨星體自轉的一個質點質量為m，星體質量為M，星體半徑為R，則滿足：

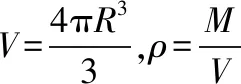
3.總結

問題1中天體穩定運行，問題2中天體剛好“漂浮”，問題3中要求天體穩定運行不瓦解，通過這三個問題情境創設，使學生徹底弄清了模型中重力、萬有引力、向心力之間的關系，從而掌握了處理天體漂浮瓦解問題的解題方法。