弧面分度凸輪機構動態特性的研究

劉 超 何雪明 黃海楠 陳小飛

(1. 江南大學江蘇省食品先進制造裝備技術重點實驗室，江蘇 無錫 214122；2. 三一重機有限公司，江蘇 蘇州 215300)

弧面分度凸輪機構因具有結構簡單，精度高，分度性能良好等優勢，被廣泛地應用于間歇分度機械中，尤其是在一些食品包裝機械中，包括飲料罐裝機、旋蓋機等。為了提高這些機械運作的精度，分析動力學性能是提高機械運作精度的重點。Taylor等[1]通過赫茲接觸理論計算出凸輪系統當中線接觸和點接觸的接觸剛度，并計算了時頻內的動態運動方程和應力情況，又在滑動接觸的條件之下，分析并比較了凸輪機構中非線性和摩擦特性情況。張興鈺等[2]考慮到彈性變形、彎曲和扭轉等因素對弧面分度凸輪機構的影響，整合剛柔耦合動力學相關的理論，通過UG、ADAMS、ANSYS 3個建模和工程分析軟件建立凸輪機構的剛柔耦合動力學模型，并通過仿真分析闡述了不同因素對整個弧面分度凸輪機構動態特性的影響情況。馮立艷等[3]先利用ADAMS對已建好的弧面分度凸輪機構模型進行剛柔耦合運動學仿真分析，以此來驗證該模型的正確性，再對該機構處在不同機構參數下進行動力學仿真分析，從而獲取不同參數情況下主從動件之間接觸力的變化曲線圖。劉言松等[4]通過虛擬樣機技術和多體動力學理論對弧面分度凸輪機構進行動力學仿真分析，這為后續凸輪機構的動力學研究創造了一種新的途徑與方法。Livija[5]將主從件的柔性、整個機構當中非線性和阻尼等因素考慮進去，構造出凸輪、從動件及驅動軸系統集成一體的凸輪機構模型，以此來分析其動力學特性情況，并驗證分析了從動件的穩定性及逼進穩定情況的條件。為了得到精確的弧面分度凸輪機構運動仿真結果，必須考慮構件的柔性條件。因此，如何建立合適的分析模型一直是實現該機構剛柔耦合運動仿真的核心問題。本研究擬基于虛擬樣機技術，在ADAMS軟件的基礎上結合ANSYS軟件建立剛柔耦合動力學模型，通過對該模型設置不同的凸輪轉速、阻尼等運動參數，進一步分析其角速度、角加速度和接觸力等運動性能的響應情況，旨在為該機構后續的動力學建模、動力學優化等研究提供參考。

1 弧面分度凸輪機構的建模

弧面分度凸輪機構在建模過程中，先需要對弧面分度凸輪的運動參數及幾何機構參數進行確定，再利用雙三次樣條曲面算法重構出弧面分度凸輪的輪廓面；然后在此基礎上，根據已知的參數對弧面分度凸輪、主動軸、分度盤、滾子、從動軸及載荷盤6個部件進行三維建模，并完成整個部件的裝配。

1.1 弧面分度凸輪三維模型的建立

弧面分度凸輪的主要設計參數如表1所示，根據其具體參數可完成弧面分度凸輪模型的建立。

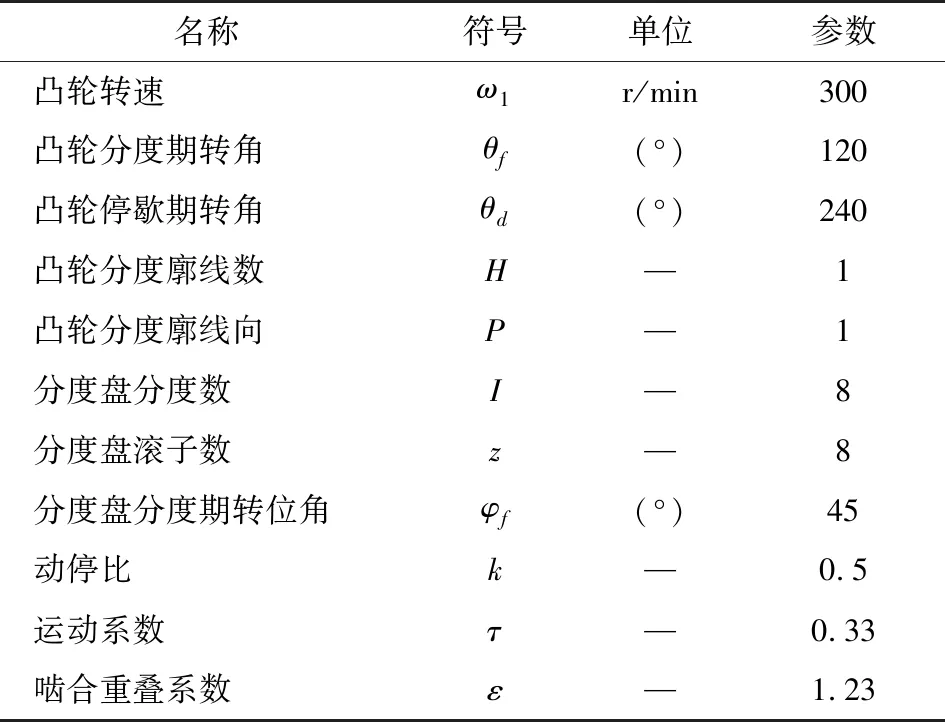
表1 弧面分度凸輪機構的運動參數

弧面分度凸輪具體建模過程：根據表1中弧面分度凸輪機構參數，結合C++導出弧面分度輪廓面的設計模塊，輸入其相應的參數，即可生成分度期工作輪廓面的點云數據，再將點云數值保存為txt文件；通過輪廓面重構模塊讀取txt文件，通過樣條曲面重構算法，顯示出重構后弧面凸輪分度期重構面，將4個重構后的分度期曲面導出成IGES格式；當4個弧面分度凸輪輪廓面IGES格式文件分別導入UG后，在已有的4個弧面分度凸輪輪廓面的基礎上，通過旋轉命令完成2個弧面分度凸輪分度期曲面；在得到2個分度期面的基礎上，根據表1的參數，對弧面分度凸輪進行建模、曲面合并、多余的工作輪廓面進行切除，再通過“旋轉”“拉伸”等命令，便完成凸輪主體建模[6]。其實體模型如圖1所示。

圖1 弧面分度凸輪實體Figure 1 Body of globoidal indexing cam

1.2 弧面分度凸輪機構的裝配

1.2.1 弧面分度凸輪機構三維模型的建立 完成弧面分度凸輪的建模，根據已知參數對弧面分度凸輪、主動軸、分度盤、滾子、從動軸以及載荷盤等6個部件進行三維建模，弧面分度凸輪機構的結構參數如表2所示；最后根據構造完成的三維模型，完成弧面分度凸輪機構的裝配。

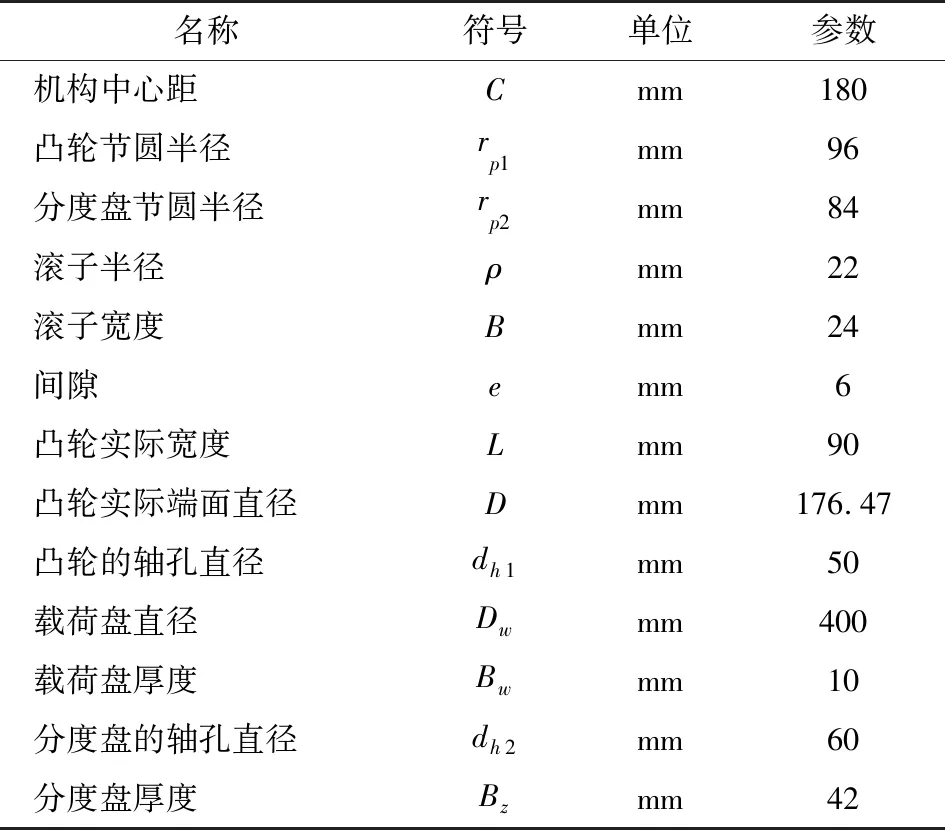
表2 弧面分度凸輪機構幾何結構參數

1.2.2 弧面分度凸輪機構中各個部件的裝配 弧面分度凸輪機構中部件的運動關系主要分為三類：固定連結關系、轉動關系和共軛接觸關系。

(1) 固定連結關系是指凸輪機構在工作過程中，2個零部件之間相對位置一直保持不變的關系。其中，輸入軸與弧面分度凸輪，輸出軸與分度盤，輸出軸與載荷盤之間均為此種關系[7]。

(2) 轉動關系是指2個零部件之間存在一定相對轉動的關系。其中，輸入軸與機架，輸出軸與機架，各個滾子與分度盤均為此種關系。

(3) 共軛接觸關系是指弧面分度凸輪與滾子之間所存在的相對運動關系。根據表2中的安裝尺寸，完成整個弧面分度凸輪機構中各部件間裝配關系。

根據以上弧面分度凸輪機構參數，完成了弧面分度凸輪機構中各個部件的裝配之后，還需要干涉檢測方法，檢查整個弧面分度凸輪機構是否存在缺陷[8]。其各部件裝配示意圖如圖2所示。

1. 滾子 2. 分度盤 3. 輸入軸 4. 載荷盤 5. 弧面分度凸輪 6. 輸出軸

圖2 弧面分度凸輪機構的三維裝配模型

Figure 2 3D assembly model of Globoidal Indexing Cam Mechanism

2 弧面分度凸輪機構運動特性分析與優化

2.1 弧面分度凸輪機構多剛體仿真模型的建立

研究重構后弧面分度輪廓面的動態特性，需對已經裝配完畢的弧面分度凸輪機構模型進行運動仿真分析。將在UG中建立弧面分度凸輪機構的整個三維裝配模型保存為“Parasolid”中間格式文件，導入到ADAMS軟件中，得到整個弧面分度凸輪機構的動力學實體模型。

弧面分度凸輪仿真模型包括以下主要條件的設置：

(1) 環境的設定：對弧面分度凸輪機構所處的環境進行定義，主要包括重力場[9]。

(2) 材料屬性設定：完成導入弧面分度凸輪機構模型之后，需要對弧面分度凸輪機構的各個部件材料進行設置。

(3) 約束關系的設定：輸入軸和輸出軸2個部件與大地之間建立旋轉關系，輸入軸與弧面分度凸輪之間建立固定約束關系，而輸出軸與載荷盤和分度盤之間建立固定約束關系，8個滾子與分度盤之間也建立固定約束關系。

(4) 接觸力的定義：由于接觸關系，弧面分度凸輪在旋轉過程中，與滾子之間產生一定的接觸力，只有通過這兩者之間的接觸力才能實現分度盤的運轉。因此，在弧面分度凸輪機構進行運動仿真分析過程之中，需要通過添加接觸力來模擬與分析真實運轉情況[10]。

在弧面分度凸輪機構運轉過程中，從動件上各個滾子分別與弧面分度凸輪進行接觸。因此，該2個零部件之間會有接觸力，而弧面分度凸輪與滾子之間建立的接觸關系為單次碰撞，則采用沖擊函數法(Impact)顯示更加合理。根據赫茲接觸理論，阻尼對機構產生的能量損耗在總損耗能量所占的比例中是較小的。因此，取比較小的阻尼系數。

接觸剛度按式(1)計算：

(1)

在式(1)中彈性模量E*按式(2)計算：

(2)

式中：

E*——彈性模量，N/mm2；

E1——凸輪的彈性模量，N/mm2；

μ1——泊松比；

E2——滾子的彈性模量，N/mm2；

μ2——泊松比。

當量半徑按式(3)計算：

(3)

式中：

R1——凸輪當量半徑，mm；

R2——滾子接觸點的當量半徑，mm。

取E1=2.12×105N/mm2，E2=2.19×105N/mm2；μ1=0.289，μ2=0.3，令R1=R2=22 mm，則計算出K=5.218×105N/mm。

在ADAMS界面中設定接觸力，設置非線性指數為e=1.5，阻尼系數為C=60 N·s/mm，穿透深度為d=0.1 mm。具體參數設置，如圖3所示。

(5) 驅動設定：在弧面分度凸輪和大地之間的旋轉副上增加電機旋轉的驅動，設置順時針旋轉，主動件的轉速ω1=300 r/min=1 800 r/s。

通過以上5個步驟的參數設置，由此便完成了整個弧面分度凸輪機構的運動仿真模型的建立[11]。

2.2 弧面分度凸輪機構運動學仿真

在仿真前需要設定合理的參數，一方面，將驅動轉速條件設定為300 r/min；另一方面，為了選用運動仿真的可靠性更好、計算精度更高的求解器。仿真完畢后，進入ADAMS后處理模塊中查看仿真結果。為了校核重構之后弧面分度凸輪輪廓面的正確性，以分度盤作為研究對象，分析其運動規律是否符合理論值。同時，以分度期作為弧面分度凸輪主要研究過程，對仿真之后分度盤上角位移、角速度和角加速度與理論上修正正弦運動規律曲線進行對比與分析。

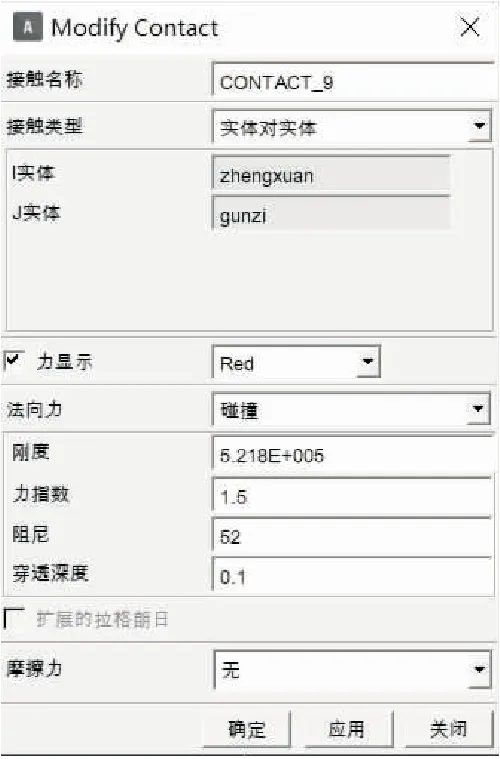
圖3 ADAMS中Impact接觸力設定Figure 3 Contact parameters setting

圖4為多剛體模型的角位移、角速度和角加速度在ADAMS中的仿真結果，可以看出，在進入分度期后，角速度出現了輕微的波動，而角加速度的振動較為明顯。但是，整體趨勢與運動規律為修正正弦加速度相一致。所以，本研究中所建立的凸輪模型是正確的。

2.3 弧面分度凸輪剛柔耦合動力學模型創建

2.3.1 柔性體的建立 由于弧面分度凸輪機構多用于高精度、高轉速的應用場合，屬于比較復雜的多體變形系統。因此，為了讓模型更加準確、仿真更精確，考慮到部件的彈性變形，需要建立弧面分度凸輪機構的剛柔耦合動力學模型。

弧面分度凸輪機構在高速運行并在接觸力、慣性力及負載作用下，難免造成機構產生扭轉變形、彎曲變形等，機構中輸入軸和輸出軸的影響最為明顯。由于輸入軸長度比較小，具有相對較大的剛度，可忽略其產生的彈性變形。因此，為了更好地研究弧面分度凸輪機構動態情況，本研究將弧面分度凸輪機構中輸出軸視為柔性體，而其他部件視為剛性體。柔性體模型建立過程如圖5所示。

(1) 將輸出軸導出“.x_t”格式的中性文件。

(2) 將輸出軸導入ANSYS當中，并按照表3設置材料屬性；然后將其網格單元類型定義為三維8節點單元solid85，采用自由網格劃分的方法來劃分輸出軸的網格，從而建立輸出軸的有限元模型。

(3) 在輸出軸與機架的旋轉中心建立結點，以此作為外部結點與剛性構建的連接。同時劃分剛性區域，將其導出成.mnf 中性格式文件。

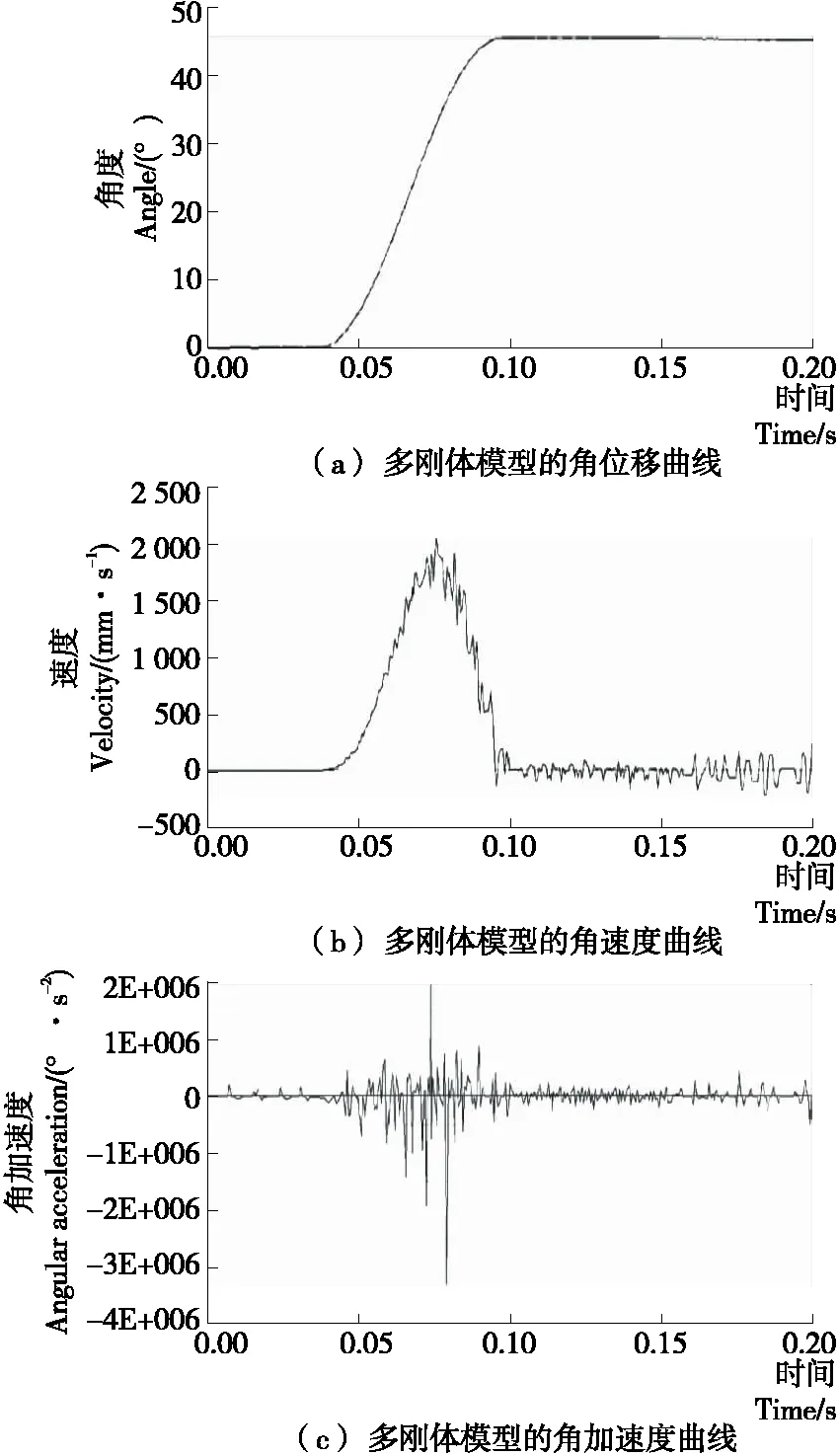
圖4 弧面分度凸輪多剛體運動仿真分析結果Figure 4 Simulation results of multi rigid-body motion of globoidal indexing cam

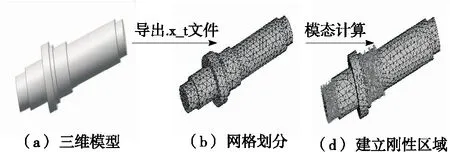
圖5 輸出軸柔性體建模過程Figure 5 Modeling process of output shaft flexible body

2.3.2 弧面分度凸輪剛柔耦合模型的建立 在原有運動仿真模型的基礎上，先將輸出軸替換為柔性體模型，然后刪除原有的運動副約束，在輸出軸上重新建立約束關系，從而完成剛柔耦合動力學模型的建立[12]，其剛柔耦合動力學模型如圖6所示。

3 不同工況下弧面分度凸輪機構動態特性

在弧面分度凸輪機構從動件旋轉過程當中，其速度會發生周期性的變化，尤其在高速工況下顯得更為明顯，主動件和從動件兩部件之間將會產生動載荷的沖擊。同時，還有其他因素將會對弧面分度凸輪機構的動態性能產生影響。而影響其動態性能的主要因素有以下幾個：弧面凸輪機構結構參數、工況、加工精度和安裝誤差等。本試驗重點研究轉速和阻尼系數對弧面分度凸輪機構動態特性的影響。

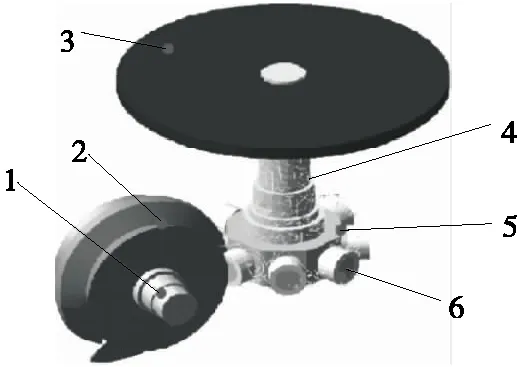
1. 輸入軸 2. 弧面分度凸輪 3. 載荷盤 4. 輸出軸 5. 分度盤 6. 滾子

圖6 弧面分度凸輪機構剛柔耦合動力學仿真模型

Figure 6 Rigid-flexible coupling dynamic simulation model of globoidal indexing cam mechanism

3.1 轉速對弧面分度凸輪機構動態性能的影響

為了滿足不同轉速工況下的要求，需根據具體應用場合設定相應的轉速，載荷盤的厚度為10 mm，不考慮載荷盤上的載荷，設定轉速為300，600，800，1 000 r/min，以此來分析弧面分度凸輪機構中不同轉速對其自身動態性能(角加速度、接觸力)的影響。

由圖7、8可知，凸輪轉速對整個機構的動態特性有顯著的影響。尤其在分度期過程，隨著弧面分度凸輪轉速的提高，分度盤角速度和接觸力都呈現逐步增大的趨勢。然而，一方面，隨著弧面分度凸輪轉速的提高，一個周期內接觸力波動次數逐步變少，在一定程度上能夠降低弧面分度凸輪與滾子之間碰撞次數，進而降低弧面分度凸輪的工作輪廓曲面的磨損；另一方面，弧面分度凸輪轉速的提高將會直接導致角加速度相應地增加，進而導致整個弧面分度凸輪機構的慣性力快速地增大，這對弧面分度凸輪動態特性是不利的。

然而，中國要打造離岸國際商事法庭仍有較多的工作需要開展。其中，如何吸引當事人選擇中國法律或者中國國際商事法庭管轄是首要問題。當前，最高人民法院采取的主要措施是安排有豐富審判經驗和能夠熟練運用中英文的資深法官擔任國際商事法庭的法官，并組建國際商事專家委員會。該做法能夠增強當事人對中國國際商事法庭的信心，但還遠遠不夠，我們還需要在兩個方向上同時努力：一個是國內商事制度的完善，另一個是國際商事法庭規則的設計。

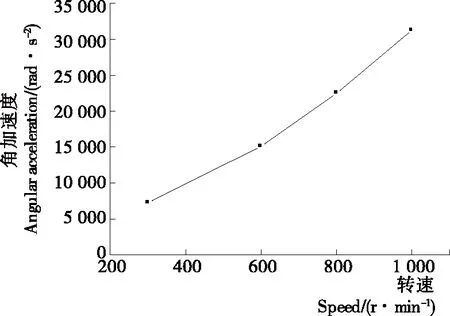
圖7 轉速與角加速度之間的變化趨勢Figure 7 The changing trend between rotational speed and angular acceleration

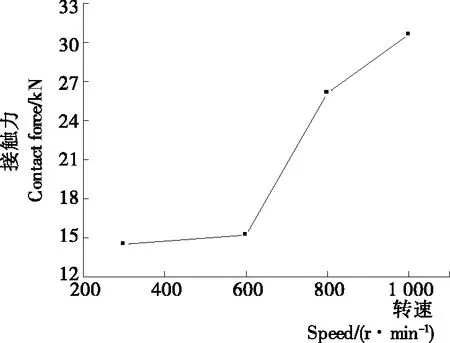
圖8 轉速與接觸力之間的變化趨勢Figure 8 The changing trend between speed and contact force

3.2 阻尼系數對弧面分度凸輪機構動態性能的影響

由于弧面分度凸輪始終接觸于滾子，而阻尼的大小會對該接觸關系產生影響。因此，為了研究不同阻尼對弧面分度凸輪機構動態特性的影響，需要對弧面分度凸輪機構不同的阻尼進行對比與分析，本研究不考慮載荷盤上的負載，設載荷盤的厚度為10 mm，設阻尼系數分別為60，100，150，200 N·s/mm，以此來分析弧面分度凸輪機構的不同阻尼系數對其自身動態性能的影響。

如圖9、10所示，隨著阻尼系數值的增大，分度盤的最大角加速度值將會先減小再增大，而滾子與分度盤之間的接觸力會隨著阻尼系數的增大而上升。

隨著阻尼系數的增加，其對弧面分度凸輪機構將產生較大的影響。分度過程中，在角加速度值由正轉負的中間時刻，凸輪將對滾子產生橫越沖擊，導致其產生最大角速度值。

在弧面分度凸輪機構一個運動周期內，隨著阻尼系數的提高，分度期內接觸力波動次數正在逐步減小。在分度期橫越沖擊時刻，接觸力的波動將會隨著阻尼系數的增加而相應地增加。因此，橫越沖擊的波動正比于阻尼系數。在弧面分度凸輪機構中停留期時，由于滾子與凸輪之間基本上無明顯的受力情況，所以接觸力和角加速度無明顯的波動，其數值基本上為零。因此，在停留期，阻尼系數對分度期中弧面分度凸輪機構的接觸力影響不大。

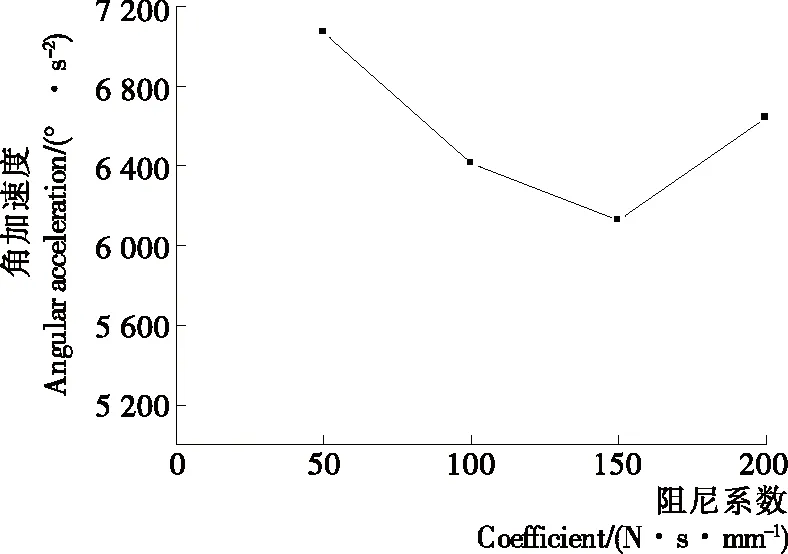
圖9 阻尼系數與角加速度之間的變化趨勢Figure 9 The trend of variation between damping coefficient and angular acceleration

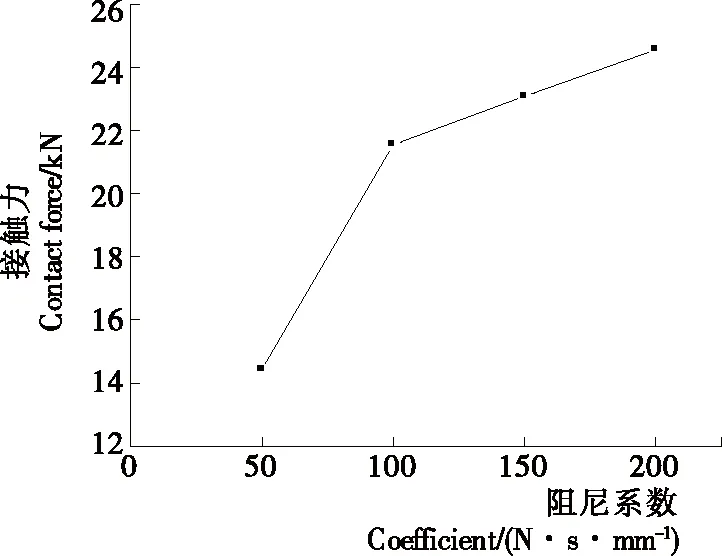
圖10 阻尼系數與接觸力之間的變化趨勢Figure 10 Variation trend between damping coefficient and contact force

4 結論

通過以上分析可知，在整個弧面分度凸輪機構中，需將轉速分別對弧面分度凸輪與均勻分布在分度盤上滾子之間接觸力和角加速度的影響考慮進去，選取最合理的轉速參數，這對提高整個機構的動態特性起到至關重要的作用。而阻尼系數將對整個機構的動態特性產生一定影響，尤其在橫越沖擊時，角加速度和接觸力變化最為明顯，弧面分度凸輪與滾子之間的阻尼將在一定程度上防止角加速度方向的改變，這將導致整個機構出現較大的波動現象。因此，在后續的設計中，采用合理的阻尼系數，能夠緩解整個機構的明顯波動現象，減少其對機構的沖擊力，保證其穩定性。