基于熵權TOPSIS法的節水灌溉方式選擇
崔世彬,宋艷艷,趙維志
(1.蓬萊市農村水利處,山東 蓬萊 265600;2.蓬萊市平山水庫管理所,山東 蓬萊 265600)
我國人均水資源占有量約為2 100 m3,為世界人均水資源占有量的1/4。2016年全國總用水量6 040.2億m3,其中農業用水3 768.0億m3,占總用水量的62.4%。農業灌溉是我國用水大戶,發展節水灌溉是發展節水農業的基礎。然而節水灌溉的方式有很多,在實際應用中,設計者會面對從多種節水灌溉方式中選取一個最優的設計方式,而選擇時必須綜合考慮諸多因素的影響,因此節水灌溉方式的優化選擇是一個多目標決策問題。
為了科學合理地選擇灌溉方式,張慶華等運用層次分析法對節水灌溉方式進行了優化選擇,門寶輝等運用灰色關聯投影法選擇井灌區最優節水灌溉方式。多目標決策方式中各因素指標之間往往是有一定聯系而不是相互獨立的,盡管他們之間的關系不明確,但是實際上卻是存在的。因此各個指標權重的確定,會不可避免地受到人為因素的影響,TOPSIS優化法可以很好地克服這個問題。本文采用TOPSIS法進行節水灌溉方式優化選擇。
1 原理與方法
TOPSIS是系統工程中有限方式多目標決策分析的一種常用方法,對樣本資料無特殊要求,使用靈活簡便。他通過歸一化后的數據規范化矩陣,找出多個目標中最優目標和最劣目標(分別用理想解和負理想解表示),分別計算各評價目標與理想解和負理想解的距離,獲得各目標與理想解的貼近度,按理想解貼近度的大小排序,以此作為評價灌溉方式優劣的依據。貼近度取值在0~1之間,該值愈接近1,表示相應的評價目標越接近最優水平;反之,該值愈接近0,表示評價目標越接近最劣水平。
用于節水灌溉方式的優選建模步驟如下:
1)建立節水灌溉方式的決策矩陣。設適合的節水灌溉方式有m種,有n個評價指標,則決策矩陣為A=(aij)m×n。
2)對節水灌溉方式決策矩陣進行標準化處理。處理時評價指標要同趨勢化,因此要將低優指標(成本型指標)轉化為高優指標(效益型指標)。

3)確定節水灌溉方式的評價指標熵權wj。根據信息熵的定義求解輸出熵Dj和指標的差異度Kj,從而計算出熵權 wj。


4)建立考慮指標權重的決策矩陣Z′,并進行歸一化得出歸一化的矩陣Z。
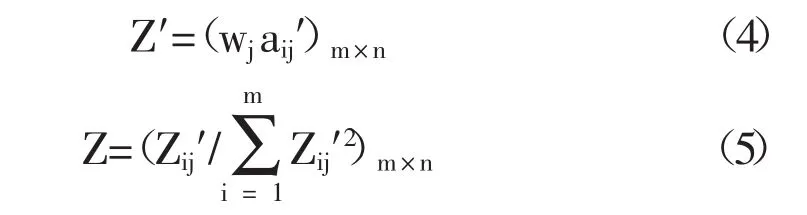
5)確定節水灌溉方式優化指標的理想解Z0=[Z01,Z02,…,Z0n]和負理想解]。


7)計算各節水灌溉方式指標值與理想解的相對接近度Gi。
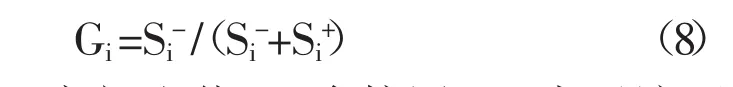
Gi在0~1之間取值,Gi愈接近1,表示該評價對象越接近最優水平;反之,Gi愈接近0,表示該評價對象越接近最劣水平。
8)根據Gi大小對節水灌溉方式進行排序,Gi的順序就是灌溉方式優劣的順序。
2 應用實例
某節水灌溉項目有管道灌溉、噴灌、滴灌、小管出流灌溉4種方式(分別為方式A、B、C、D)供選擇,以國民經濟評價(凈現值E1、收益率E2、投資回收期E3、效益費用比E4)、技術指標計算(灌水均勻度T1、灌水強度T2、灌溉水利用率T3)、專家社會評價(安全可靠性H1、地形適應性H2、作物適應性H3、農民歡迎程度H4、便于施工程度H5)為評價指標進行節水灌溉方式的優選。評價指標見表1。
下面用基于熵權TOPSIS法選擇最優節水灌溉方式。
由表1可以看出,地形適應性H2指標不具有區分節水灌溉方式的作用,故該指標不包括在模型之內,即模型中的評價指標為11個。11個指標中投資回收期E3為成本型指標,其他10個為效益型指標。
經優化計算,最終得相對接近度
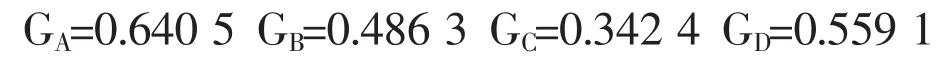
對 Gi進行排序,GA≥GD≥GB≥GC,可見節水灌溉方式的優劣順序為方式A、方式D、方式B、方式C。此結果與文獻[2]的結果(方式A、方式B、方式D、方式C)雖有差別,但最優方式卻相同,而且用熵權TOPSIS法對節水灌溉方式進行優化,各個方式的相對接近度差別較大,易于區分。
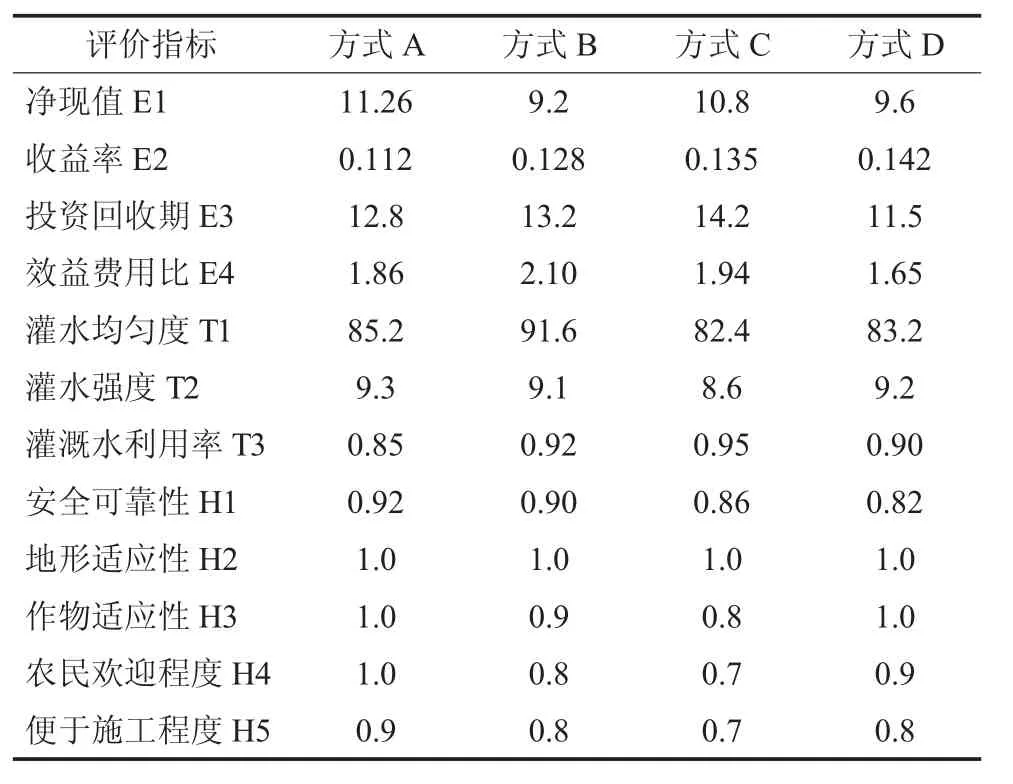
表1 評價指標
3 結語
本文應用基于熵權TOPSIS法對節水灌溉方式進行優化,建立了評價指標的TOPSIS模型,通過實例驗證取得了可靠的評價結果。應用TOPSIS法對節水灌溉方式進行優化選擇,克服了人為賦予權重的隨意性,具有簡單實用的特點。從結果來看,用熵權TOPSIS法對節水灌溉方式進行優化,各個方式相對接近度差別較大,易于區分。由于實例中選取的評價指標無法涵蓋全部的節水灌溉影響因素,模型在應用中還需不斷完善。

