基于粒子群算法的RBF神經網絡零件表面缺陷分類

文/岳曉峰 劉天

1 引言

金屬工件精加工表面缺陷主要分為三類：劃痕、斑點、凹坑。金屬工件表面缺陷常用分類方法有三種：人工神經網絡分類法、支持向量機分類法和樹狀分段線性分類法。人工神經網絡分類算法對非線性擬合問題表現突出，模擬大腦神經網絡處理、記憶信息的方式進行信息處理。在1985年，Powell提出了多變量插值的RBF函數（Radical Basis Function，簡稱RBF）方法。1988年，Moody和Darken提出了一種神經網絡結構，即RBF神經網絡，屬于前向類型的神經網絡，它具有以任意精度逼近連續函數，特別適合于解決分類問題。RBF神經網絡的缺點是，若RBF神經網絡結構和參數選取不當，則會導致網絡收斂慢甚至造成網絡發散。針對標準RBF神經網絡算法的不足，本文提出了一種基于粒子群算法改進的RBF神經網絡的分類方法，利用粒子群算法優化RBF神經網絡的基函數的中心xi、方差σ、輸出權值ω，并對網絡進行訓練提高分類準確率。

2 RBF神經網絡模型的建立

2.1 RBF神經網絡結構

RBF網絡的結構與多層前向網絡類似，它是一種三層前向網絡。第一層為輸入層，由信號源節點組成；第二層為隱含層，隱含層的單元數量由所描述問題決定，隱含層單元的變換函數是對中心點徑向對稱且衰減的非負非線性函數；第三層為輸出層，對輸入模式的作用作出響應。從輸入空間到隱含層空間的變換是非線性的，而從隱含層空間的輸出層空間變換是線性的。由輸入層、單一隱含層和輸出層構成的RBF神經網絡結構如圖1所示。

RBF神經網絡的激活函數一般使用RBF函數（如Gaussian函數）作為激活函數，以輸入向量和權值向量之間的距離||dist||作為自變量的。RBF神經網絡激活函數的一般表達式為：

2.2 RBF神經網絡的學習算法

RBF神經網絡學習算法需要求解的參數有3個：基函數的中心xi、方差σ、隱含層到輸出層的權值ω。根據RBF函數中心選取的方法不同，RBF神經網絡有多種學習方法，如隨機選取中心法、自組織選取中心法、有監督選取中心法和正交最小二乘法等。本文采用K-均值聚類方法，學習算法具體步驟如下。

（1）網絡初始化。

隨機選取h個訓練樣本作為聚類基函數中心xi(i=1,2,…,h)。

（2）將輸入的訓練樣本集合按最近鄰規則分組。

按照xp與中心為xi之間的歐式距離將xp分配到輸入樣本的各個聚類集合?p(p=1,2,…,P)中。

（3）重新調整基函數的聚類中心。

計算各個聚類集合?p中訓練樣本的平均值，即新的基函數聚類中心xi，如果新的基函數聚類中心不再發生變化，則所得到的xi即為RBF神經網絡最終的基函數中心，否則返回①，進入下一輪基函數中心的求解。

（4）求解方差σi。

RBF神經網絡的基函數為Gaussian函數，因此方差σi可由下式求解。

式中，cmax為所選取聚類中心之間的最大距離。

（4）計算隱含層和輸出層之間的權值。

隱含層至輸出層之間神經元的連接權值可以通過最小二乘法直接求得ω，計算公式如下。

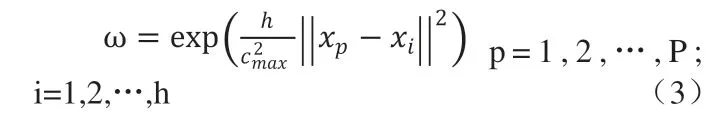
2.3 RBF網絡分類器的設計

圖2：RBF神經網絡分類流程圖

圖3：PSO算法流程圖

在RBF神經網絡結構圖中，輸入層到隱含層的權值是1，隱含層的激活函數為徑向基函數，關鍵要求解出基函數的中心xi、方差σ、隱含層到輸出層的權值ω。首先運用K-均值聚類方法確定基函數的中心xi，并通過公式（2）的計算求解出方差σi，由公式（3）求得隱含層到輸出層的權值ω。由分類數決定輸出節點數。將標準RBF神經網絡應用于金屬工件表面缺陷分類處理。金屬工件表面缺陷分類3類，那么劃痕的期望輸出向量為L1（1,0,0），斑點的期望輸出向量為L2（0,1,0），凹坑的期望輸出向量為L3（0,0,1）。經過以上步驟，便構建完成RBF神經網絡分類器的設計，RBF神經網絡分類器的分類流程圖如圖2所示。

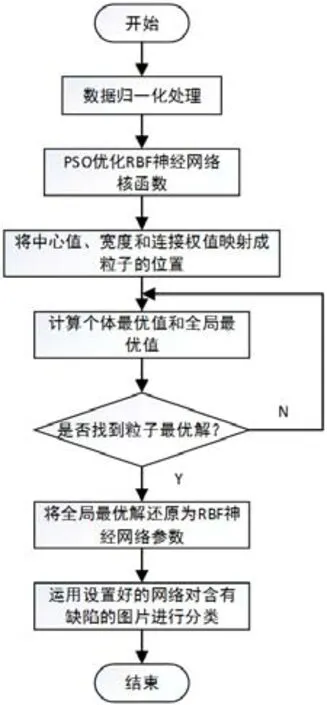
圖4：PSO改進的RBF神經網絡分類流程圖

3 基于粒子群算法改進的RBF神經網絡模型的建立

3.1 粒子群算法

粒子群算法，也稱粒子群優化算法或鳥群覓食算法（Particle Swarm Optimization），是由J. Kennedy和R. C. Eberhart等提出的一種新的進化算法。在PSO算法中每個優化問題的潛在解都可以想象成搜索空間中的一只鳥，稱之為“粒子”。在每一次迭代中，粒子通過跟蹤兩個“極值”來更新自己，第一個極值是粒子本身所找到的最優解，這個解叫作個體極值pbest；另一個極值是整個種群當前找到的最優解，這個極值是全局極值gbest。粒子群算法的流程圖如圖3所示。其具體過程如下

（1）粒子群初始化，包括群體規模N，每個粒子的位置xi和速度vi。

（2）計算每個粒子的適應度值Fit[i]。

（3）用適應度值Fit[i]和個體極值pbest(i)比較，若Fit[i]>pbest(i),則用Fit[i]替換掉pbest(i)。

（4）用適應度值Fit[i]和全局極值gbest(i)比較，若Fit[i]>gbest(i),則用Fit[i]替換掉gbest(i)。

（5）根據公式：

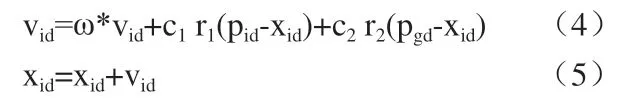
式中c1，c2為學習因子，更新每個粒子當前的速度和位置。

（6）如果滿足結束條件（尋找到個體極值pbest和全局極值gbest或者達到最大循環次數）退出，否則返回（2）。

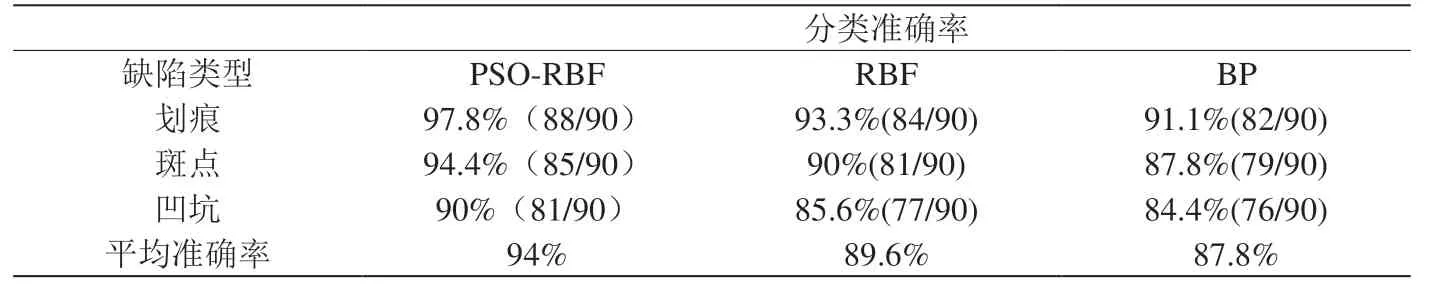
表1：分類準確率

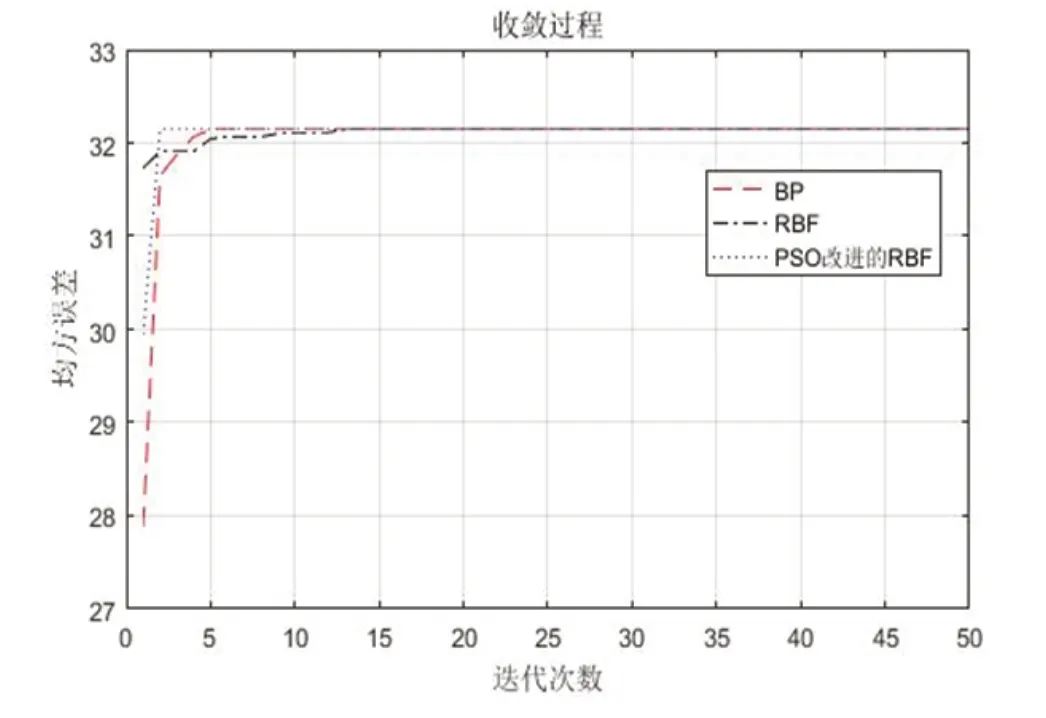
圖5：3種方法性能對比圖

3.2 權重改進的粒子群算法

PSO算法最大的優點是不需要調節過多的參數，但是算法中的群體規模N、慣性權重ω、加速度常數c1和c2卻直接影響算法的性能和收斂性。其中慣性權重ω是最重要的參數。增大ω的值可以提高算法的全局搜索能力，減小ω的值可以提高算法的局部搜索能力。常見的PSO算法有自適應權重法、隨機權重法和線性遞減權重法等。本文采用線性遞減權重法確定PSO算法中的慣性權重。針對PSO算法容易早熟及后期容易在全局最優解附近產生振蕩現象，采用了線性遞減權重法，即使慣性權重依照線性從大到小的遞減，其變化公式為：

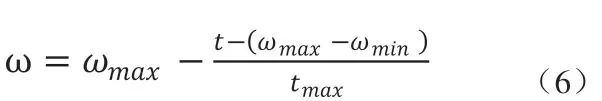
式中ωmax為慣性最大值；ωmin為慣性最小值；t為當前迭代次數。

線性遞減權重法的計算步驟如下：

（1）隨機設置各個粒子的速度和位置。

（2）評價每個粒子的適應度，將粒子的位置和適應值儲存在粒子的個體極值pbest中，將所有pbest中最優適應值的個體位置和適應值保存在全局極值gbest中。

（3）更新粒子位移和速度：

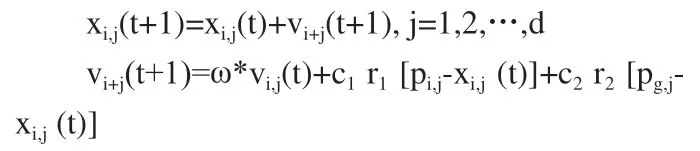
（4）更新權重：

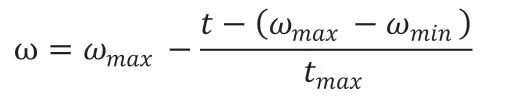
（5）將每個粒子的適應值與粒子的最好位置比較，如果相近，則將當前值作為粒子最好的位置。比較當前所有的pbest和gbest，更新gbest。

（6）當算法達到其停止條件，則停止搜索并輸出結果，否則返回（3）繼續搜索。

3.3 基于PSO改進的RBF神經網絡分類算法實現

基于PSO 的RBF神經網絡分類具體過程：

（1）讀取輸入樣本和測試樣本。

L1，L2，L3分別表示劃痕、斑點、凹坑。每種缺陷的訓練樣本和測試樣本各100幅圖片。

（2）數據歸一化處理。

在建立神經網絡之前需要對訓練樣本和測試樣本數據進行歸一化處理，提高神經網絡的收斂速度和泛化能力，同時增加每個樣本之間的關聯信息，使其擬合效果更好。實驗中將數據歸一化到[0,1]之間并找出樣本X中的最大值Xmax和最小值Xmin，用如下公式計算：

Xi表示歸一化后的數據，這樣所有的數據都在[0,1]之間。

（3）RBF神經網絡核函數參數的優化。

初始化粒子群及RBF神經網絡，建立PSO算法中粒子與神經網絡連接權值之間的映射；計算各粒子之間的適應值，將神經網絡的方差作為PSO算法的適應函數，適應度函數值越大說明粒子的位置越好，其公式如下：

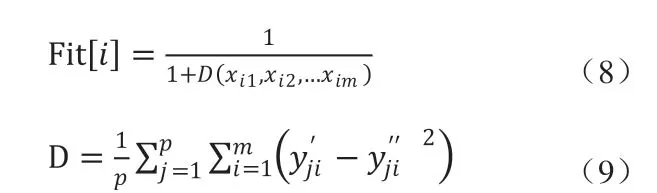
式中Fit[i]為第i個粒子的適應度值，D為神經網絡的方差，p為訓練樣本總數，m是輸出層的節點數，為實際輸出值，為期望輸出值；根據公式（4）和（5）更新粒子的速度和位置；重復上述步驟，直到找到粒子的最優解或者最大循環次數。

（4）運用經過PSO改進后的RBF神經網絡對測試樣本進行缺陷分類，分類流程圖如圖4所示。

圖7

4 實驗結果比較與分析

本文通過MATLAB R2016a軟件進行編程，為了驗證算法的有效性，首先使用標準RBF神經網絡算法和PSO改進的RBF神經網絡算法以及之前研究的BP神經網絡算法進行性能對比實驗，實驗結果如圖5所示。從圖中可以看出在取得相同均方差時，PSO改進的RBF神經網絡所需的迭代次數更少。

為驗證程序的穩定性，將程序運行20次求得迭代次數平均值，如圖6所示。

運用RBF神經網絡、PSO改進的RBF神經網絡和BP神經網絡對金屬工件表面的缺陷進行分類。采集含有缺陷的圖片300幅，其中含有劃痕、斑點、凹坑三種缺陷的圖片各100幅。三種典型缺陷圖片如圖7所示。

對抽取的測試樣本進行試驗，分類結果如表1所示。

從表1中可以看出，劃痕的分類識別準確率最高，達到97.8%，其次是斑點和凹坑，缺陷的平均識別率在94%。為證明本文中PSO改進的RBF神經網絡分類方法優于RBF神經網絡和BP神經網絡分類方法，進行對比試驗。采集含有缺陷的圖片300幅，其中含有劃痕、斑點、凹坑三種缺陷的圖片各100幅，統計結果如圖8所示。

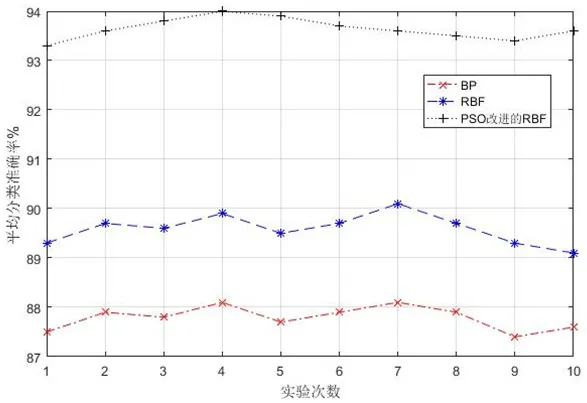
圖8：分類方法對比實驗

5 結論

本文應用PSO算法對RBF神經網絡基函數的中心xi、方差σ、隱含層到輸出層的權值ω進行訓練尋求最優值，消除了人為因素選取RBF神經網絡中心參數導致網絡收斂慢甚至造成的網絡發散問題。在標準PSO算法的基礎上引進線性遞減權重法對ω進行優化，提高了PSO算法的收斂速度和精度。對比實驗表明PSO算法改進的RBF神經網絡比標準RBF神經網絡和BP神經網絡分類識別準確率有較大提高。