基于SAP2000的錯層結構動力彈塑性時程分析

鄒仁華，張 浩，張 瓊，許嘉偉，楊 帆

（西安科技大學 建筑與土木工程學院，陜西西安 710054）

0 引言

為了解決錯層框架結構中常出現短柱以及錯層節點處傳力路線差等現象，本文提出了帶鋼管混凝土柱的新型錯層結構。目前國內外對此類新型錯層結構抗震性能方面的研究少之又少，為此，本文利用SAP2000彈塑性時程分析，對此類工程的抗震性能進行系統的研究。

1 錯層結構計算模型

1.1 CG1結構模型概述

本文所選擇的工程計算模型為錯層框架結構，在2、4軸線處錯層，布置位置對稱。建立鋼筋混凝土錯層結構將其標記為GC，建立的帶鋼管混凝土柱的錯層結構標記為XGC。建筑結構總高度為16.5m，總長度為24m，總寬度為10.8m。首層高度為4.5m，其他層為3m。錯層部位首層為3.6m，錯層高度。

混凝土為C35，鋼管選擇Q235，該建筑的抗震設防烈度為8度（0.2g），設計地震分組為第二組，場地類別為Ⅱ類。該工程選擇柱下獨立基礎，并采用不上人屋面。錯層框架結構中的節點無特殊處理，其結構的平立面布置圖如圖1所示。

1.2 其他工程模型的建立

鋼管混凝土構件的受力情況有別于一般混凝土構件，其主要影響因素是鋼管對混凝土的約束作用。參照韓林海對鋼管混凝土柱的研究[1]，以及對方形鋼管混凝土柱抗剪性能方面的研究，本文設計了五個工程建模方案，如表1所示。

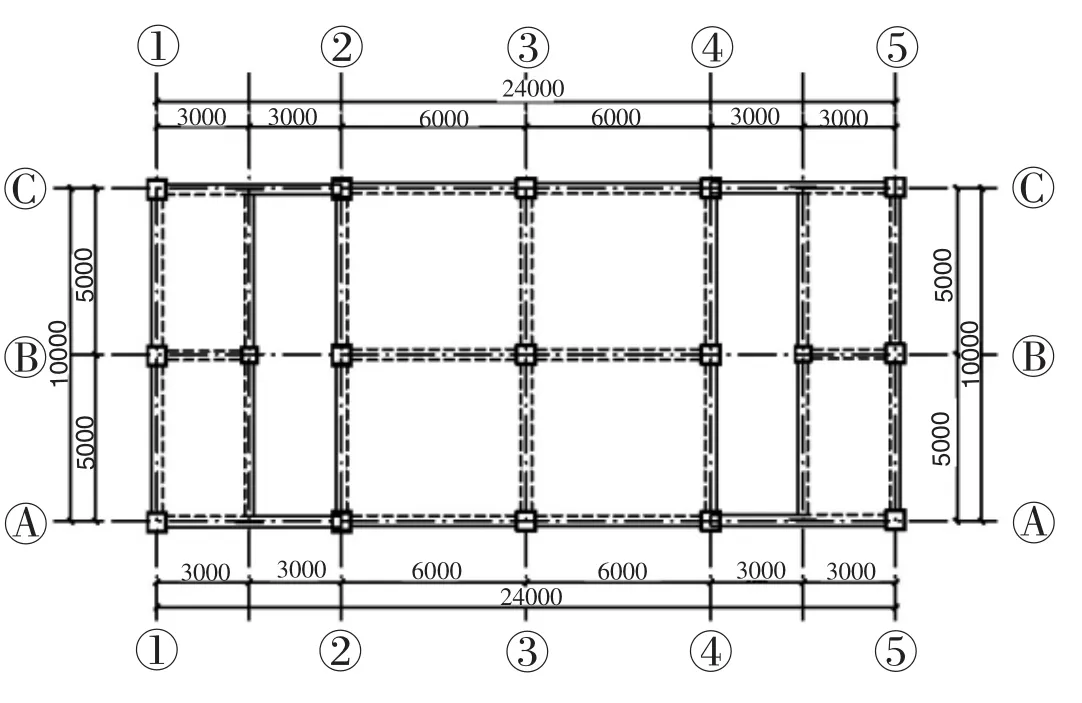
圖1 GC1結構平面圖

表1 設計主要參數及等級

2 工程有限元模型的建立

2.1 結構模型假定

（1）材料屬性的定義

在建模過程中，對材料進行各向同性的假設，其表現為材料的行為獨立于荷載方向或材料朝向，剪力行為與膨脹行為不耦合，并且不受溫度的影響。一般混凝土和鋼材都符合該假定。各向同性材料應變與應力以及溫度變化的力學、熱性能的關系如下式所示：

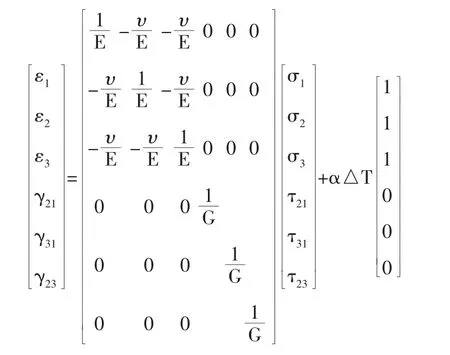
式中：E為楊氏彈性模量；υ為泊松比；G為剪切模量；α為熱膨脹系數。

（2） SAP2000模型簡化假定

依賴于《混規》5.1.5條對剛度樓板的相關規定，本文建模中樓板采用剛性隔板假定，有限元建模中用薄殼單元（SHELL）來模擬分析。該假定減少了結構的計算自由度，從而縮減后期系統中求解方程的數量，使程序計算效率大大提升。

將梁柱構件簡化為空間桿，并都用桿單元進行建模，只考慮單元的剪切變形和軸向變形。并將處于錯層的梁柱連接節點假定為理想鉸接。

2.2 結構模型的建立

（1）單元的剖分

工程模型在進行有限元分析之前，需要對其相關構件進行單元網格劃分，其最低要求是保障每個研究對象的計算精度。本文SAP2000工程中殼單元采用自動網格劃分，并將最大剖分長度設置為1.2m。

（2）質量源的定義

SAP2000程序提供給我們質量源的定義方式有三種，本文選擇“來自荷載”這一方法，并遵循《荷載規范》選擇荷載組合方式，即恒荷載加1/2的活荷載的組合方式。

（3）錯層模型的處理

錯層結構會出現在同一層中兩個不同標高的樓板，本文在SAP2000建模時采用的方法是按照兩個標準層來建模，其相當于樓板大開洞的情況，從而實現錯層樓板的布置。

（4）鋼管混凝土柱截面的定義

本文對鋼管混凝土柱建模，定義材料分別為鋼管選用Q235，截面設計選擇“箱型截面”；混凝土選用C35并設定為約束模式，截面設計中采用矩形截面。利用Xtract進行鋼管混凝土柱截面設計計算，并得出相關鉸屬性的定義參數。

應用軟件SAP2000進行結構模型建立，其由各種梁柱桿系單元以及薄殼單元組成有限元空間分析模型，如圖2所示。

2.3 鉸屬性特征值有效性的驗證

通過SAP2000對文獻[1]的試驗模型進行建模并對其進行Pushover分析，并將輸出的模型頂點的荷載位移曲線與試驗結果對比，從而驗證本文提及的鉸屬性特征值的確定方法是否有效，具體結果如下圖3和圖4所示。

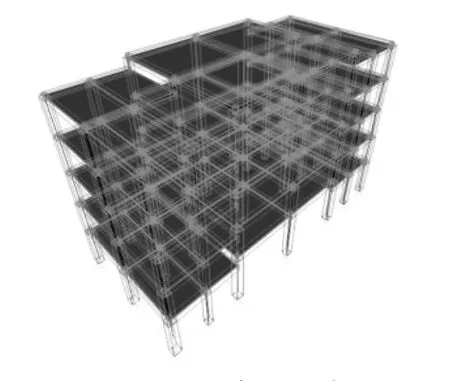
圖2 GC1有限元空間分析模型

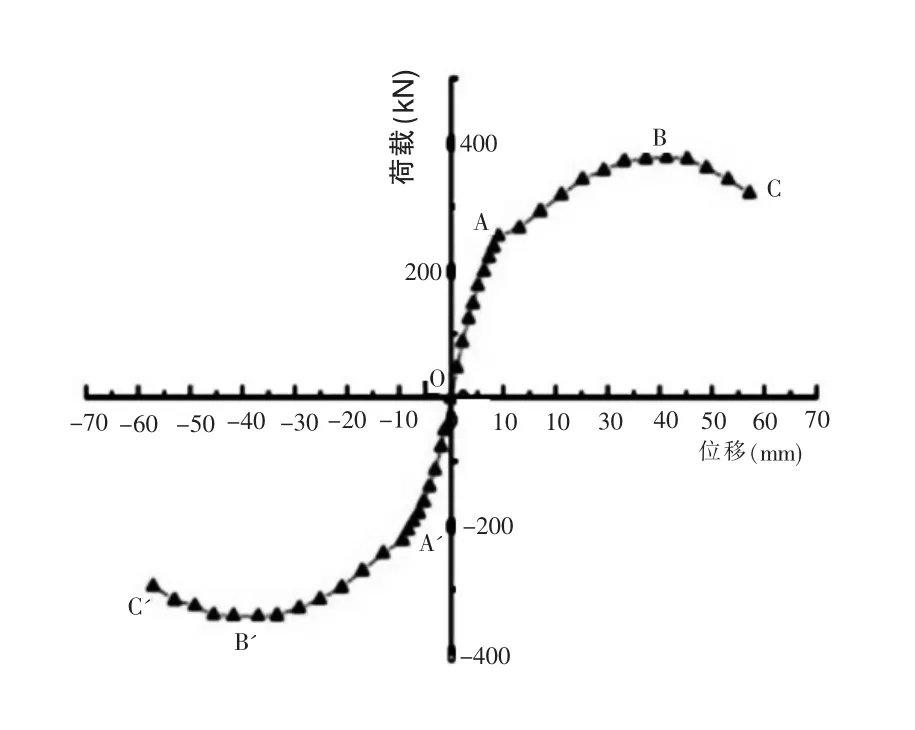
圖3 頂點位移試驗結果圖示

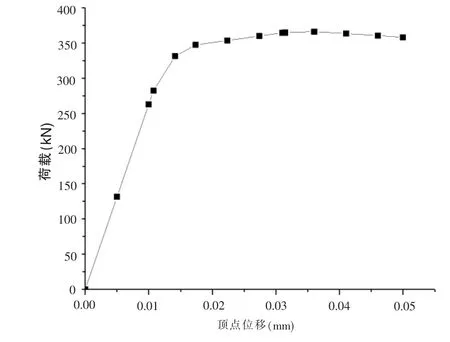
圖4 頂點位移Push-over分析結果圖示

在加載工程中整體結構經歷了彈性、彈塑性工作階段和破壞階段。試驗結構破壞時塑性鉸的出現順序是先在底層梁端出現塑性鉸，然后是二層梁端，最終底層柱底出現塑性鉸而導致框架破壞，塑性鉸的發展過程符合“強柱弱梁”的設計理念。在加載的過程中，控制位移所施加的側向力為F=46.86~191.17kN時，荷載-位移曲線可近似為線性段，結構處于彈性階段；當側向荷載F=219.61kN時，結構出現屈服，靠近施載底層梁端出現塑性鉸；側向位移△=41.28mm時，結構承受最大側向力F=375.57kN，此時柱底出現塑性鉸，結構的承載力開始下降。整體而言，試驗得到的荷載-位移曲線較光滑[2]。

通過SAP2000建立試驗模型，并利用Push-over計算的基地剪力-位移曲線如圖4所示。從圖中可以看出，模型計算試驗模型的極限承載力為F=366kN，計算的頂點位移為△=36.4mm，可得出兩者的誤差分別為2.5%和11.8%。在模型分析中塑性鉸的出現順序和試驗結果顯示中相一致，并在頂點位移為△=36.4mm時，模型中的塑性鉸全部出現，標志著構建端部各個截面逐漸開始退出工作，結構整體的承載力出現顯著下降的趨勢。

根據基底剪力-位移相關數據的對比和塑性鉸的發展情況進行分析對比，依據分析結果可以得出建立的此類分析模型中塑性鉸自定義的方法是切實可行的，能夠有效確定鋼管混凝土柱塑性鉸的特征值相關參數。

3 動力時程分析

3.1 時程分析理論

《建筑抗震設計規范》（GB 50011-2010）第 3.6.2條規定“不規則且具有明顯薄弱部位可能導致地震時嚴重破壞的建筑結構，應按本規范有關規定進行罕遇地震作用下的彈塑性形分析[3]。此時，可根據結構特點采用靜力彈塑性或彈塑性時程分析方法。對于高階振型且比較復雜的結構，由于在第一階振型結構運動中結構本身的薄弱部位不一定會顯現出來，或者當結構雖然產生了較大的扭轉效應，但是并沒有在靜力非線性分析中得到反應，這類結構就需要應用動力彈塑性分析方法來分析罕遇地震作用的位移反應[4]。

本文選擇兩條實際地震波以及一條人工波，分別為Lan Zhou 1波、EL-Centro波和Tang Shan EW波，對上面提及的5個工程模型進行時程分析。其通常采用的積分方法主要有Newmark法、Wilson法和HHT（Hiber-Huges-Taytor）法，本文選擇HHT法進行數值計算。HHT法其實是對Newmark法的改進與提升，用系數對結構的運動方程進行調整，由Huges在1987年的時候提出。

3.2 時程分析結果

在三條時程波作用下，對各工程模型進行非線性時程分析，本文從結構變形、樓層剪力和塑性鉸的發展這三方面進行對比分析，探討了設計方案中提及的兩個變量參數對工程模型的影響狀況，對XGC模型抗震性能的影響因素進行評估。

選擇LanZhou1波時程分析輸出在X方向的數據進行分析，下面分別給出了各個模型在Lan Zhou1波下的層間位移變化曲線和層間基底剪力圖，如圖5和圖6所示。

圖5、圖6分別給出了LanZhou1波作用下，各個模型的層間位移和樓層剪力的數值變化曲線。通過對比，可得出下面相關理論：

（1）GC模型在X向的層間位移曲線既不符合典型剪切型的層間位移隨層高增大而減小的趨勢，也不符合彎曲型的隨層高增加而增加的趨勢。

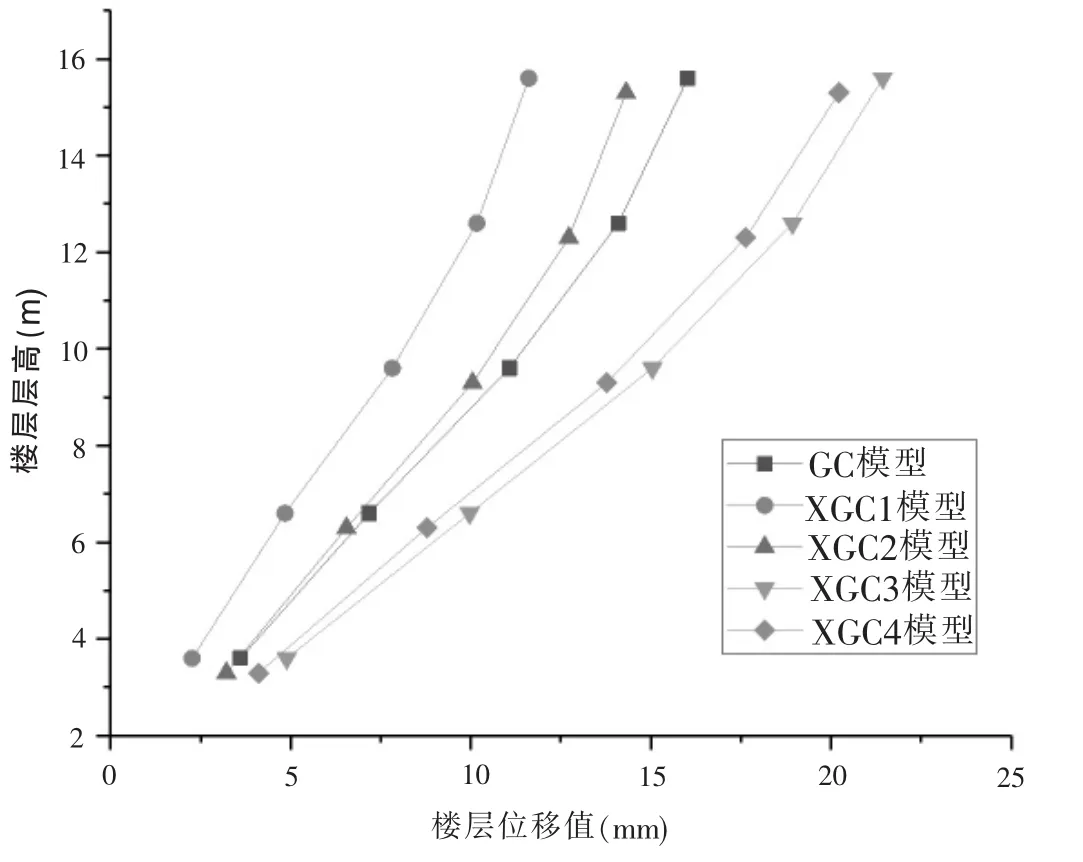
圖5 各模型層間位移LanZhou1波圖示

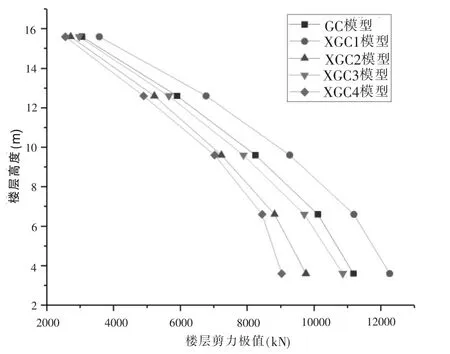
圖6 樓層剪力極值LanZhou1波圖示

（2） 圖5中，通過對模型XGC1、模型XGC2和模型XGC3、模型XGC4對比，可得出XGC模型的鋼管混凝土柱截面尺寸的增大，使得結構模型的樓層位移值也隨之增大。通過這一現象，可以看出其自身質量大于剛度增值對位移值的影響。

（3）通過圖7給出的各工程模型在LanZhou1波作用下樓層剪力極值的變化曲線，將各工程模型的剪力變化趨勢兩兩對比，能夠得出影響XGC模型樓層剪力值變化的主要因素是結構的錯層高度。

通過時程分析輸出數值的對比，得到EL-Centro波下輸出的位移值最大。特此，在上面的基礎上，提供罕遇地震下彈塑性時程分析的各個模型層間位移角的相關數值，利用抗震規范的相關規定進行驗證分析。下面對該波下的層間位移進行整理計算，結果如表2所示。

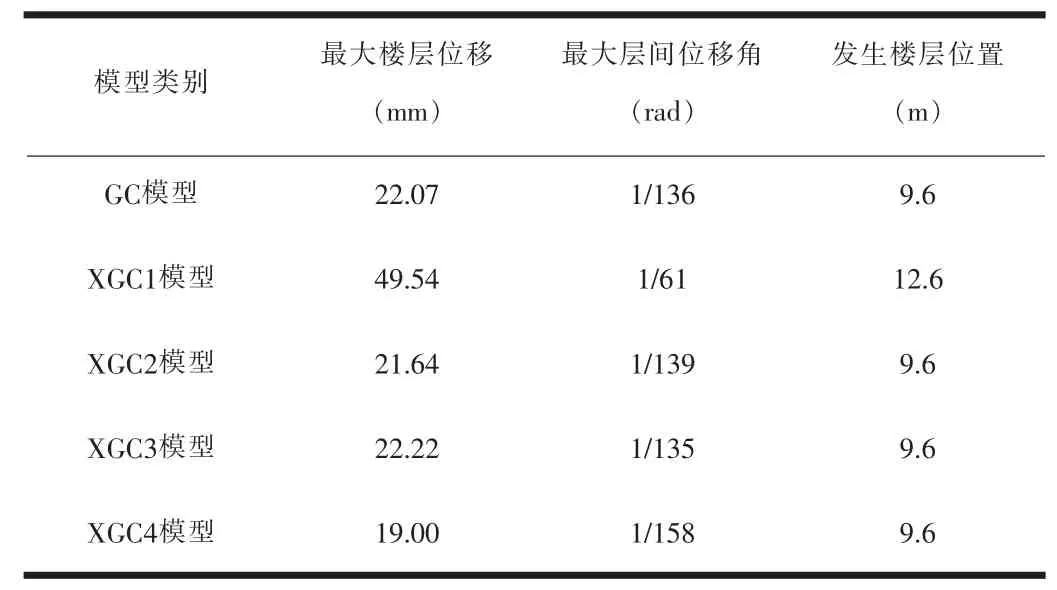
表2 各工程模型彈塑性層間位移角結果示表

（4）抗震規范中對彈塑性層間位移角的規定限值為1/50，可看出各個模型都符合該項要求。表2中XGC1模型的層間位移角為1/61，遠大于其他四個模型，并且其發生位置在12.6m處，其他的在9.6m處，可得出XGC1模型的整體剛度要小于其他模型。通過分析可發現，該現象的出現是因為相比于鋼筋混凝土構件，其側向剛度和錯層節點處傳力路徑較差，而XGC1模型的錯層高度較小無法完全發揮出鋼管混凝土柱的延性，這正是僅相比于XGC2模型也會出現層間位移突變的原因。

3.3 塑性鉸的發展

上面給出的位移、樓層剪力和層間位移角都是結構時程分析最終時刻的結果，無法反映工程真實受力的變形過程。為此，對各個工程在8度罕遇地震波作用下的塑性鉸相關結果進行整理輸出。下面以LanZhou1波為例進行相關結果輸出，如圖7所示。

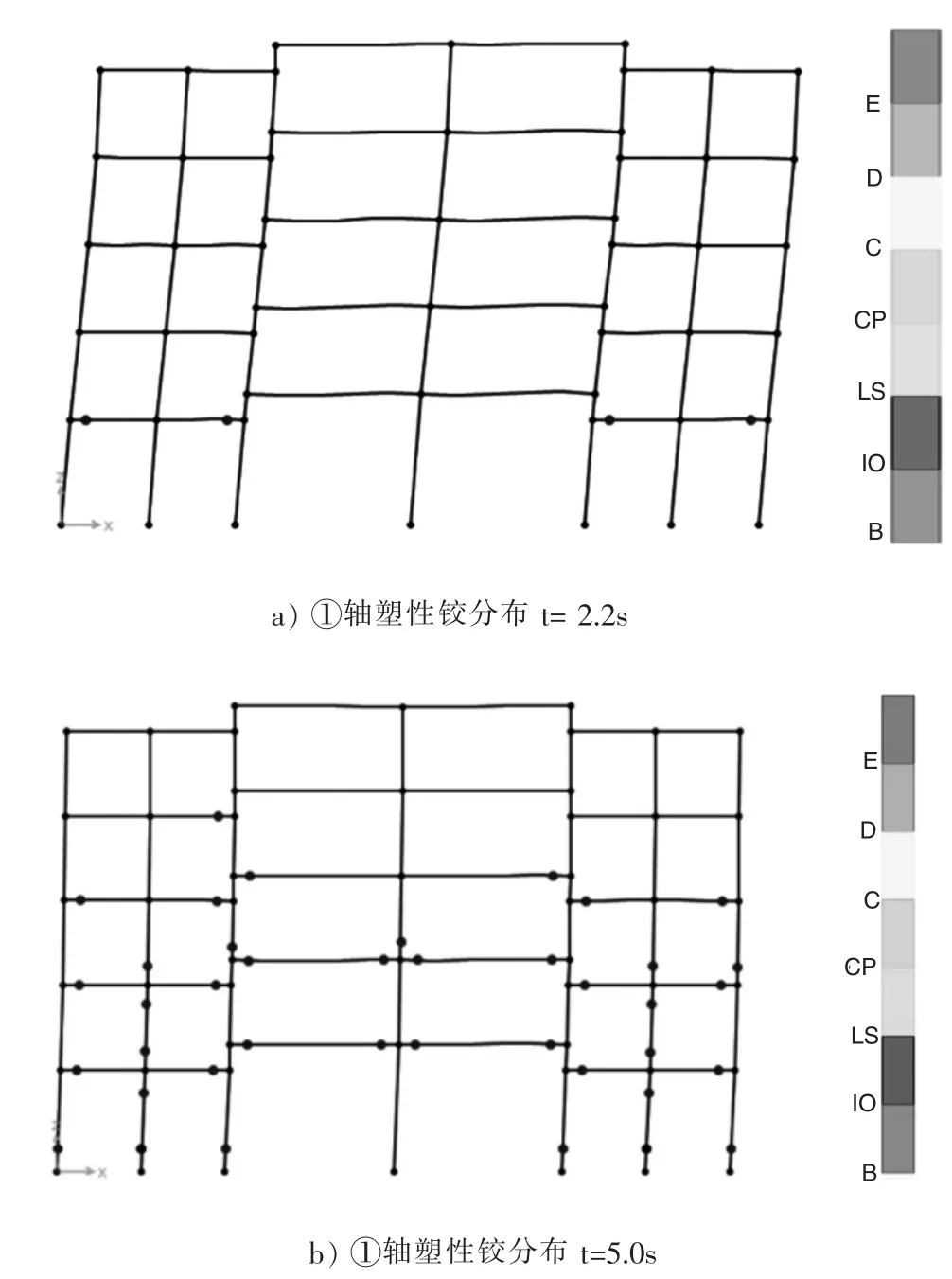
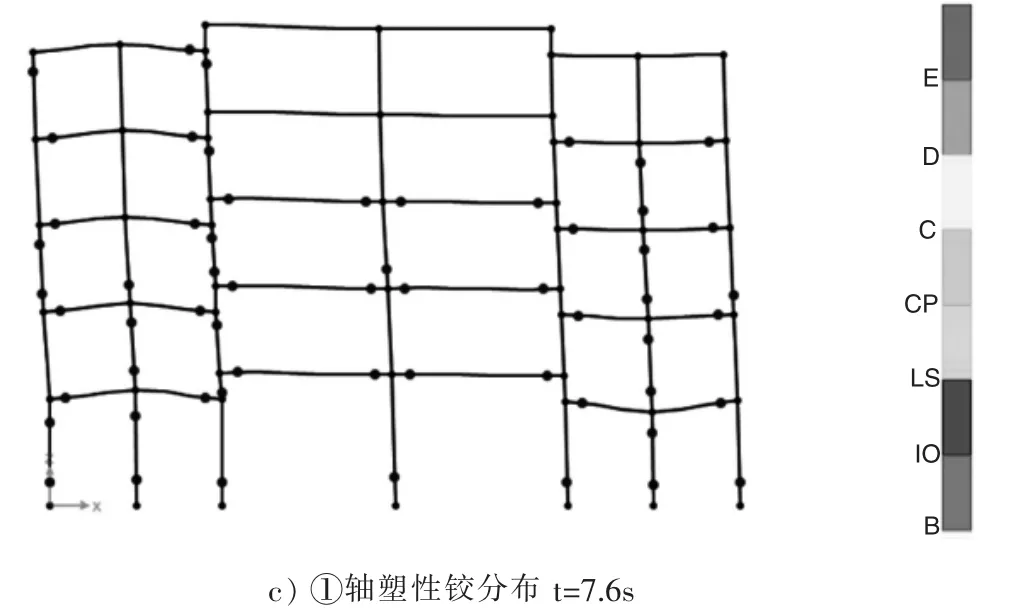
圖7 GC模型LanZhou1波作用下塑性鉸發展

圖7 給出了在LanZhou1波作用下，GC模型塑性鉸的出現情況，在2.2s時開始出現塑性鉸，先是在第二層兩端出現塑性鉸，主要集中在錯層柱兩側的梁端處；在5.0s時，即LanZhou1波幅值的極值出現時刻，逐漸在三、四層梁端處以及部分柱底端陸續出現塑性鉸，出現塑性鉸的混凝土柱主要分布于模型結構層高較低的兩側還有第三層；在7.6s時，首層柱底端首先進入破壞狀態。通過上面可以看出，建立的GC模型雖然符合“強柱弱梁”的設計理念，但是因為錯層的原因使得模型在第三層和錯層節點處出現薄弱層，讓模型的整體性變得較差。本文對其他四個帶鋼管混凝土柱的錯層結構在LanZhou1波作用下其塑性鉸的發展情況進行簡單闡述，如圖8—圖11所示。

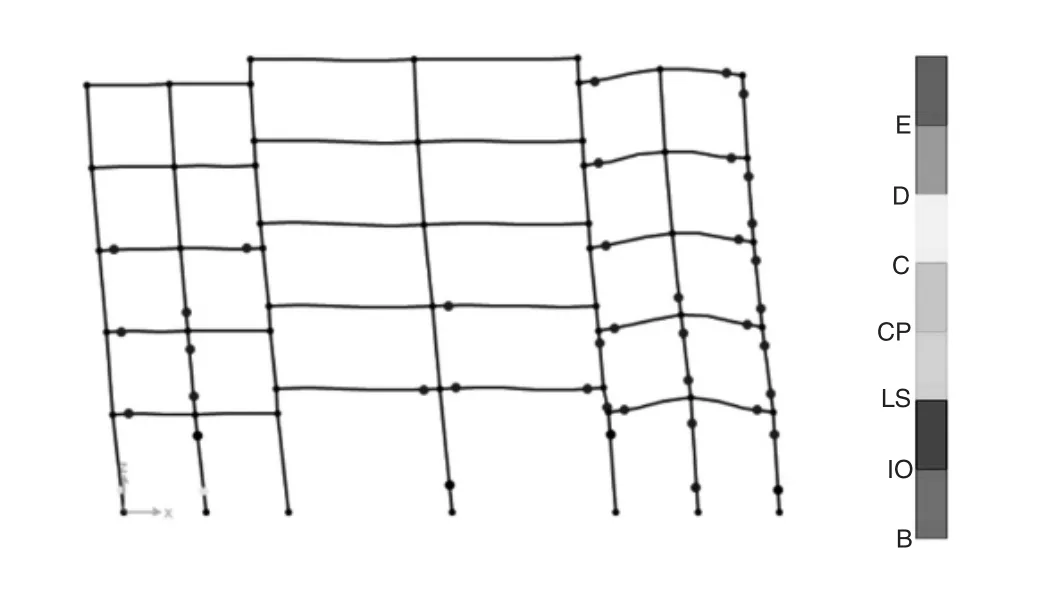
圖8 XGC1模型塑性鉸發展（t=6.0s）

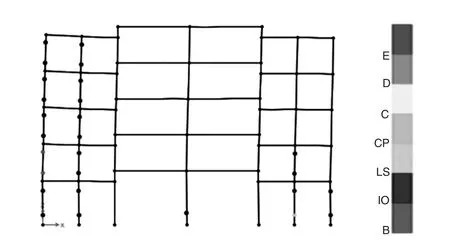
圖9 XGC2模型塑性鉸發展（t=4.7s）

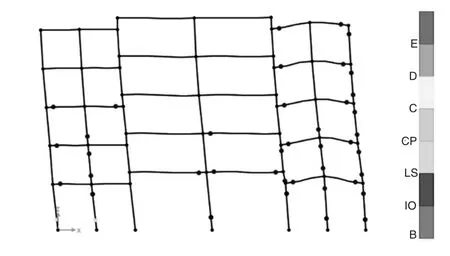
圖10 XGC3模型塑性鉸發展（t=6.0s）

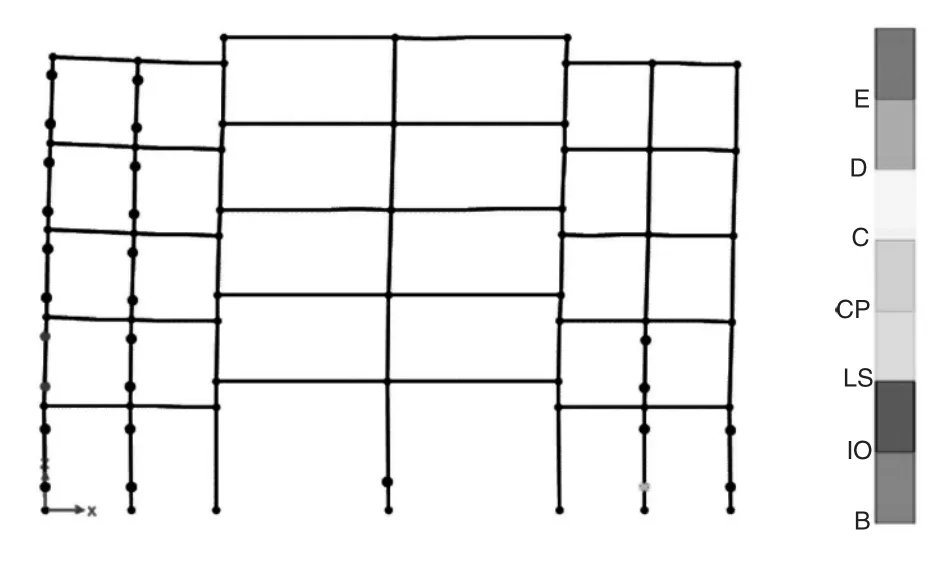
圖11 XGC4模型塑性鉸發展（t=9.2s）

圖8 —圖11展示出了四個帶鋼管混凝土柱的新型錯層框架結構的塑性鉸發展情況，可以得出模型XGC1和XGC2的塑性鉸首先出現在軸線2、4的底層柱的底端，而其塑性鉸極限破壞階段分別在6.0s和4.7s，并且此過程中鋼管混凝土柱上未出現塑性鉸，其主要出現在兩側的梁柱構件上。可以得出雖然300*300的鋼管混凝土柱能夠提供與GC模型相當的承載力，且其自身延性較好，但是其側向剛度較差，從而使得兩側梁柱上塑性鉸出現的較為密集，這兩個工程模型無法提供良好的抗震性能。

圖11和圖12為模型XGC3和XGC4塑性鉸的發展圖示，相比鋼管混凝土柱截面尺寸較小的模型XGC1和XGC2，其塑性鉸都是出現在2.2s時，在梁端和底層柱上陸續出現，其極限破壞階段出現時刻分別為6.0s和9.2s。可以看出鋼管混凝土柱與混凝土柱的側向剛度相近時，在一定程度上，模型中錯層高度越大，模型表現出的延性越好。

模型XGC4與模型GC相比，兩種工程模型的極限狀態出現時間分別是9.2s和7.4s，雖然后期都在第一、三層柱端出現塑性鉸，但是對比可以發現，模型XGC4僅是在2、4軸零星出現，并在錯層柱段處未出現塑性鉸。上面的種種現象表明，相比于模型GC，在地震作用下，模型XGC4表現出來了較好的整體變形能力，并且極大地改善了模型GC1的抗震性能。

對建立的五種工程模型進行動力彈塑性分析，通過對塑性鉸發展情況對比分析，可以得出模型XGC1和模型XGC2中的鋼管混凝土柱的側向剛度較小，無法改善GC模型塑性鉸的發展情況。模型XGC3和模型XGC4塑性鉸的發展情況符合“強柱弱梁”的設計理念，并且改善了原模型在錯層柱段塑性鉸的變形情況，相比較而言，模型XGC4破壞階段出現較晚，表現出了良好的抗震變形能力。

4 結語

對各個模型進行動力彈塑性時程分析，通過對比三種地震波作用下，各個模型所展示出的結構變形和樓層剪力變化曲線，可得出僅依賴框架柱等軸壓承載力替換得出的XGC模型無法滿足結構側向剛度的要求。

通過塑性鉸出現和發展的趨勢，發現GC模型在錯層柱段易出現塑性鉸，總結得出錯層結構傳力路徑差和柱段短柱等因素，正是造成該模型抗震性能差的原因。相比較其他四個新型帶鋼管柱的錯層結構，通過有限元模擬得出模型XGC1和模型XGC2雖然避免了錯層處柱段塑性鉸的出現，但其工程結構的側向剛度差，因此其結構整體性也較差。模型XGC3和模型XGC4中塑性鉸發展緩慢，未在錯層處出現塑性鉸，且相比于模型XGC3，增大錯層高度使得柱底塑性鉸退出工作的時間出現了延長。模型XGC3和模型XGC4極好地改善了模型GC的抗震性能。

通過對上面結論進行整理分析，可得出模型XGC3和模型XGC4能夠改善GC模型的抗震性能，主要表現在避免了錯層柱段處塑性鉸的出現、延長了結構出現破壞的時間，以及避免了第三層薄弱層的出現，即本文提出的XGC模型確實對錯層結構的抗震性能有極大的改善，為之后相關的工程實際應用和后期研究打下了堅實的理論基礎。