基于投影的點云配準算法
江 盟 ,蔡 勇,張建生
(1.西南科技大學制造科學與工程學院,四川 綿陽 621010;2.制造過程測試技術省部共建教育部重點實驗室,四川 綿陽 621010)
0 引言
點云配準技術是逆向工程和產品檢測中非常重要的環節。目前,點云自動配準算法中應用廣泛的是迭代最近點(iterative closest point,ICP)算法及其改進算法[1]。配準點云的初始位置是ICP算法非常重要的限制條件。該條件影響ICP算法的配準速度和全局收斂。粗配準技術能有效解決ICP算法對初始配準位置的要求。文獻[2]在逆向工程中,將多次掃描得到的點云數據先采用主成分分析(principal component analysis,PCA)粗配準,再采用ICP算法實現精細化配準。PCA算法的特點是粗配準速度非常快,但魯棒性很差。為增強粗配準的魯棒性,文獻[3]利用二維圖像提取特征點實現點云配準,但提取特征的過程相當耗時,且噪聲對算法的影響比較大。
點云配準本質是求優化解的過程[4]。其中比較重要的兩個問題是:第一,設計一個可行的評價函數;第二,采用一種有效的搜索方法[5-7]。評價函數有空間分布熵[5]、表面融合[7]等。遺傳算法對于多變量多目標的問題求解具有非常好的效果,因此許多學者在點云配準中使用遺傳算法作為搜索方法[8-10]。此外,將隨機抽樣一致性算法引入點云配準[11-12],也能達到很好的配準效果,但是其配準速度比較慢。
本文提出了一種降維處理點云數據的配準算法。首先,將配準點云投影到三個坐標平面,并且劃分平面以統計每一個格子中的點數;然后,分別求解每個投影平面的熵值,再利用遺傳算法來搜索使得三個投影平面熵值和最小的空間變換矩陣;最后,將最優矩陣作用于目標點云,實現配準。
1 點云空間位置關系評價
快速、精確地評價點云的空間位置,是點云配準中非常重要的環節。本文將點云數據的三維立體圖形經過投影降低維度到二維,再經過統計計算來評價兩片點云的空間位置關系。
1.1 信息熵的定義
對于包含N個點的點云P,將其投影到某平面得到二維投影點云P’。將投影平面的橫坐標和縱坐標均按間隔ΔL進行柵格化,統計輸入點云數據的總點數N及每個非空柵格內的點數ni,得到每個非空柵格的點云出現頻率pi為:
(1)
點云P在該平面的投影熵SE定義為:
(2)
1.2 投影
在工程制圖中,通常采用三視圖來表達物體的形狀和各部件的相對位置關系。因此,三視圖能完整地表達各部件的相對位置關系。一個物體確定后,其各個部件的相對位置關系也就確定。點云配準本質為找出點云之間的相對位置關系。因此,通過確定空間點云的投影位置,就能確定空間點云的位置關系。空間點云三坐標平面投影如圖1所示。
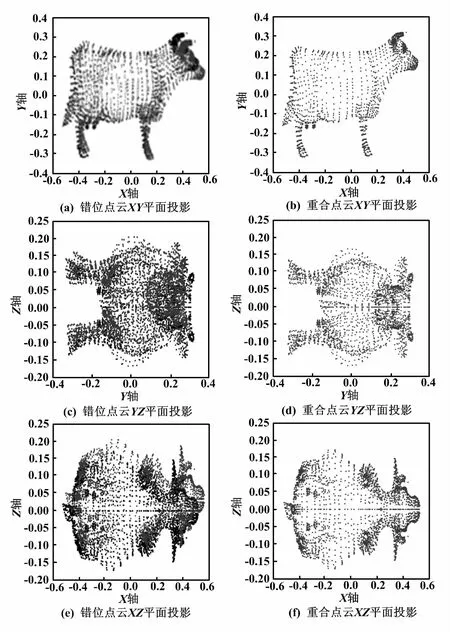
圖1 空間點云三坐標平面投影圖
由圖1可知:兩個錯位(未配準的)點云模型在二維平面的投影是不重合的,兩重合(配準后的)點云在二維平面的投影是重合的。本文基于此原理,提出了一種降維評價三維空間點云位置關系的新方法。
1.3 信息熵評價點云空間位置關系
對于待配準的兩片點云,由圖1可以看出,當兩片點云的角度沒有偏差的時候,其投影也沒有偏差。當點云角度偏差為0°時,兩片點云在該平面上的投影相對聚集。此時,投影點云分布密度的不均勻性最大。當點云角度偏差不為0°時,由于兩片點云不在同一坐標系下,故投影點云將較為均勻分布在整個投影平面上。此時,投影點云分布密度的不均勻性較小。由不同點云偏差角度可得到不同的投影點云分布,因而有望利用投影點云分布密度估計點云的空間位置。
根據空間點云僅在一個平面的投影,不能非常精確地估計點云位置關系。如在點云位置相差90°時,利用一個平面的投影尚不能估計出點云空間位置關系。而利用三個坐標平面投影熵之和,能消除點云錯位90°不能估計的情況。
將兩片點云投影到XY、YZ、XZ三坐標平面,依據式(1)和式(2)計算得到點云在XY、YZ、XZ平面的投影熵,分別為SEXY、SEYZ、SEXZ。
定義總的點云投影熵E為:
E=SEXY+SEYZ+SEXZ
(3)
從式(3)可知,點云的投影分布越密集,總投影熵就越小。
2 基于投影的點云配準
本文采用總投影熵作為遺傳算法的目標函數,來尋找空間變換的最優解。第一步是設置空間最大的變換空間;第二步是初始化目標種群并計算其適應度值;第三步是進行個體選擇、交叉和變異以產生子代個體,直到滿足設定的遺傳代數或目標函數收斂的條件來終止遺傳算法;第四步是得到最優空間變換矩陣,并應用于配準點云,得到配準結果。
2.1 變換空間
兩次掃描的點云空間坐標系是任意的,而在遺傳算法中需要設置其變換空間最大范圍。因此,需要尋找出最大變換空間。算法的求解步驟如下。
①設點云P中有N個點,點云Q中有M個點,分別計算出中心。計算式為:
(3)
(4)
②中心化點云。
(5)
③計算出兩片點云在X、Y、Z方向上的最大值和最小值。
④旋轉矩陣R參數。
對于旋轉矩陣[α,β,γ],如果確定了繞軸旋轉的角度α、β、γ,就能求解旋轉矩陣。在三維空間中,繞其中一個坐標軸最大轉動角度為2π,因此選用旋轉角度取值區間為[-π,π],則α∈[-π,π]、β∈[-π,π]、γ∈[-π,π]。
⑤平移矩陣T參數為:
(6)
(7)
(8)
2.2 編碼方案
本文使用給定長度的二進制符號串來表示群體中的個體,其等位基因由二值符號集{0,1}所組成。
①編碼。設某一參數的取值范圍為[W1,W2],采用長度為u的二進制編碼符號來表示該參數,則它共能產生2u種不同的編碼,可使參數編碼時的對應關系為:
0000L 00=0→W1
0000L 01=1→W1+σ
0000L 02=2→W1+ 2σ
… …
1111L 11=2u-1→W2
式中:W1為參數取值下限;W2為參數取值上限;u為編碼長度;σ為編碼間距。
②解碼。假如某一個體的編碼為bubu-1…b2b1,則對應的解碼公式為:
(9)
2.3 適應度函數
在遺傳算法中,個體的適應度大小決定了該個體被淘汰的概率。個體的適應度值越小,其越可能被淘汰。而在本文中,需要目標函數值越小越好,適應度值越大越好。所以,通過目標函數構造的適應度函數為:
FitnV=CE
(10)
式中:E為總投影熵;C=0.618。
2.4 算法實現
本文遺傳算法的各進化算子分別采用輪盤賭方法、單點交叉和單點變異,并將空間三坐標平面的投影熵之和作為遺傳算法的目標函數。算法步驟如下。
①最大變量域中初始化種群P,并設定最大遺傳代數G。
②種群P分別作用于目標點云,求取每次初始變換空間的X、Y、Z坐標方向最大最小值,確定最大變換空間位置。
③計算個體的目標函數和適應度值。
④選取種群中最優個體,得到其總的點云投影熵E,令全局最小總的點云投影熵Emin=E。
⑤根據適應度值進行優良個體選擇并使用最優保存策略,對選擇的種群進行交叉和變異操作,產生新一代進化種群。
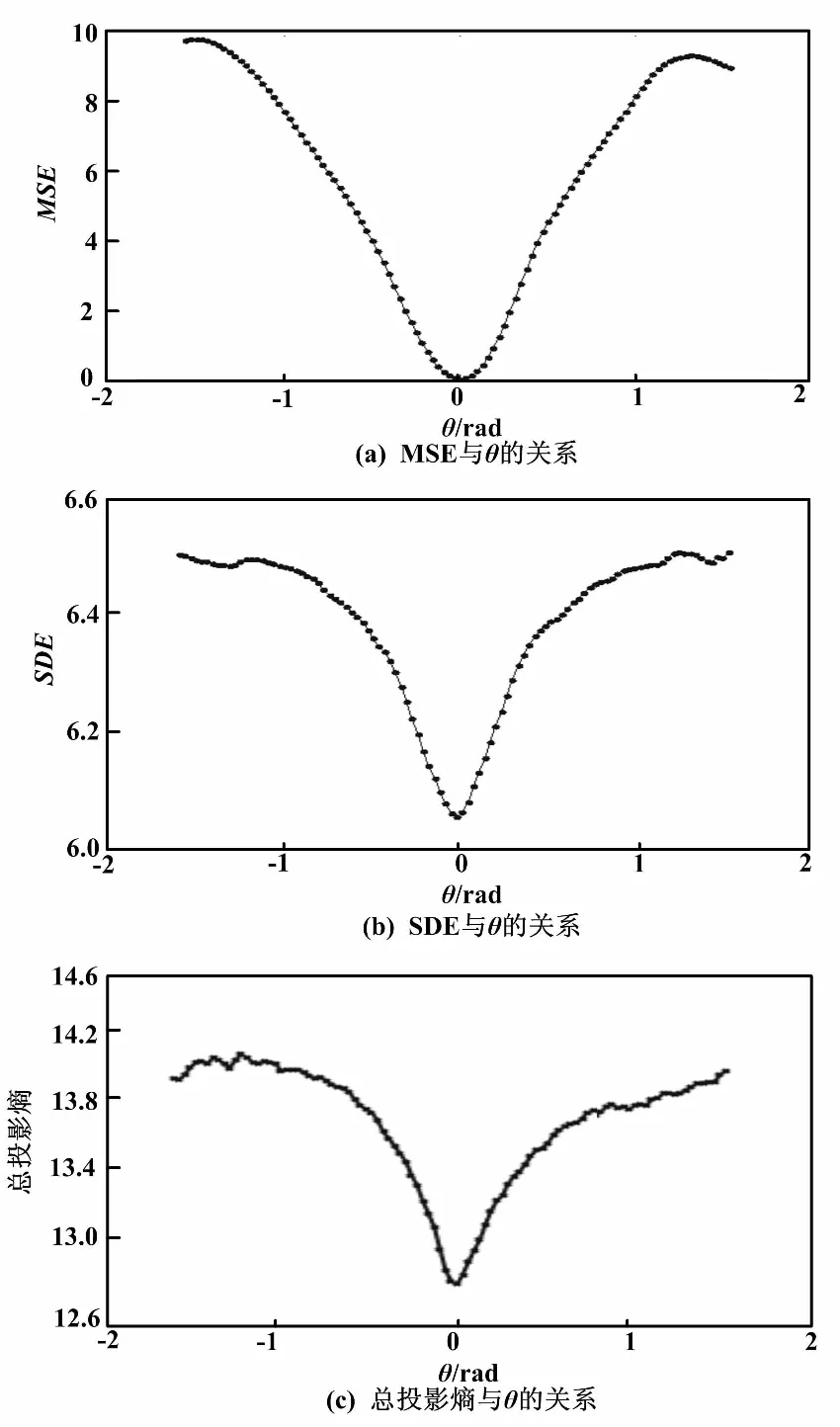
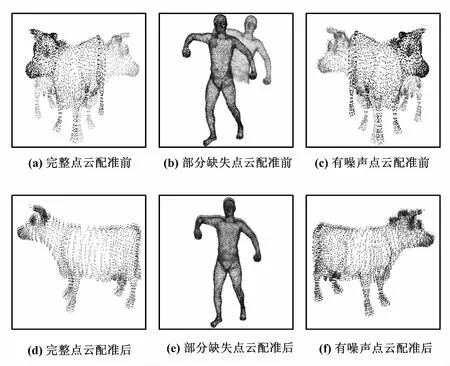
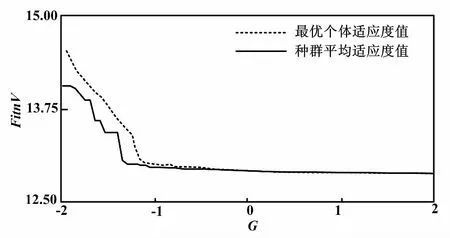
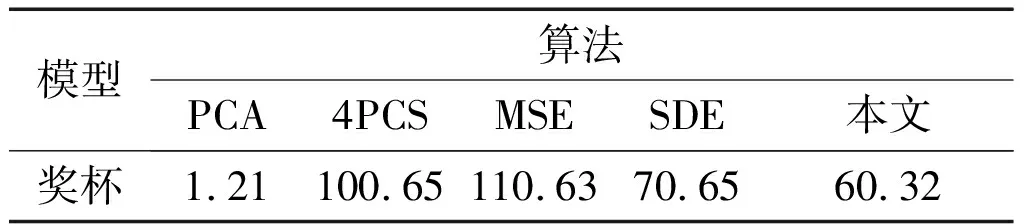
⑥求解新一代種群所有個體的適應度值FitnV,比較該代最優個體的總的點云投影熵SE′和全局最小總的點云投影熵Emin。如果E′ ⑦檢查當前代數是否達到最大代數G,以及E是否收斂。若沒有達到,則轉到步驟⑤,繼續求解;否則,輸出全局最優個體,解碼得到空間最優旋轉、平移矩陣。 ⑧更新點云位置,輸出配準點云。 基于投影的點云配準算法流程如圖2所示。 圖2 基于投影的點云配準算法流程圖 為了驗證算法的可行性、魯棒性和有效性,在Intel Core-i5、8 GB內存的Windows 7操作系統中,基于MATLAB平臺進行配準試驗。該試驗主要以有缺陷和有大量噪聲點的點云來進行驗證。 圖3 不同算法的空間位置評價示意圖 由圖3可知:MSE、SDE和總投影熵算法都能滿足空間位置的評價。當點云完全配準時,三種評價算法都是全局最小。但此過程中,MSE算法運行時間為93.159 s,SDE算法運行時間為3.135 s,本文算法(總投影熵)運行時間為2.527 s。由此說明,本文算法耗時最少。由于遺傳算法尋優時需要不斷評價個體的空間位置,因此需要頻繁的調用。而本文算法在滿足準確性要求的條件下,具有快速性的特性,很適合作為遺傳算法目標函數。 為了說明本文算法的有效性,將本文算法分別應用于完整的、部分缺失的、有噪聲的點云模型。不同類型模型的配準效果如圖4所示。由圖4可知:本文的粗配準算法對于三種點云模型都具有很好的配準效果,能夠為精配準算法提供優良的初始位置。設定最大遺傳代數G=80,初始種群的個體數為80,交叉概率為0.9,變異概率為0.09。 圖4 不同類型模型的配準效果圖 以圖4中(a)模型為例,圖5為遺傳代數與適應度值的變化關系圖。 圖5 遺傳代數與適應度值變化關系圖 圖5顯示了每一代種群適應度平均值和每一代種群中最優個體的適應度值。本文的配準算法采用遺傳算法作為搜索策略。由圖5可知:隨著遺傳代數的增加,種群朝著最優解的方向遺傳進化,最優個體也隨著遺傳進化而趨近于全局最優解。由此說明,本文采用遺傳算法求解最優空間變換矩陣是有效的。 為了驗證本文算法的優異性,選用四種粗配準算法進行比較。不同算法的配準效果對比如圖6所示。圖6(b)為文獻[2]中的PCA算法;圖6(c)為文獻[12]中四點匹配法(4-point congrugent set,4PCS);圖6(d)為文獻[6]中MSE算法;圖6(e)為文獻[5]中SDE算法。以下模型是西南科技大學獎杯,參考點云是完整的點云,目標點云是含有部分噪聲的點云。設定最大遺傳代數G=50,初始種群的個體數為40,交叉概率為0.9,變異概率為0.05。由圖6可知:PCA算法配準效果最差,4PCS和MSE算法配準效果較好,SDE算法配準效果不夠理想,本文算法效果最好。 圖6 不同算法的配準效果對比圖 不同算法運行時間對比如表1所示。 表1 不同算法運行時間對比 Tab.1 Comparison of running timeof different algorithmss 模型算法PCA4PCSMSESDE本文獎杯1.21100.65110.6370.6560.32 由表1可知:PCA算法用時最少,本文算法相對4PCS、MSE和SDE算法用時較少。再結合圖6結果,可得本文算法的配準性能最高。 本文通過計算三視圖中的投影熵來描述兩片點云的位置關系,提出了一種降維評價點云空間位置的方法。由于可以把點云配準作為優化問題處理,利用該評價方法簡單快速的特點,再采用遺傳算法作為搜索方法、投影熵作為目標函數,可以準確、快速地尋找出最優的匹配。該配準算法利用了遺傳算法,但還沒有充分挖掘遺傳算法的特性,在運行效率方面可以進一步提高。
3 試驗結果與分析
3.1 點云空間位置關系
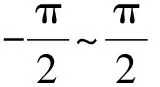
3.2 不同類型模型配準結果分析
3.3 不同粗配準算法效果比較

4 結束語

