基于特質波動率的投資組合研究

段瀟儒 鄭 旭

（上海交通大學 安泰經濟與管理學院，上海 200030）

風險與收益之間的關系一直是金融學研究的重要內容。理論上，經典的資本資產定價模型（CAPM）指出，由于投資者都持有充分分散的投資組合，風險資產的預期收益只與該資產所承擔的系統性風險有關，其特質風險不影響均衡價格。而根據Miller，存在賣空限制的情況下，投資者的異質信念會導致證券被系統性地高估，因為此時股票定價由市場上最樂觀的投資者進行，悲觀投資者的情緒無法體現在市場上，而過高的定價最終會回落，這就意味著異質信念與風險調整后的收益率成反比。Merton提出了投資者認知假說（IRH），認為由于所掌握的信息不完全，投資者只持有自己熟悉（了解風險和收益特征）的證券，在持有的組合未能完全分散的條件下達到均衡時，證券的預期收益率與特質報波動率成正比。

實證研究中，Ang等使用美國市場從1963年到2000年的股票數據，首次對公司層面的特質波動率進行了研究，以每月中的日頻數據進行Fama-French三因子回歸，用殘差的標準差度量特質波動率，發現股票特質波動率與橫截面預期收益顯著負相關，并且該現象不能由規模、賬面市值比、杠桿、流動性、成交量、換手率、買賣價差、協偏度、分析師預測分歧程度、動量等因素解釋。Ang等擴大樣本范圍，對23個發達國家市場進行檢驗，發現這一現象依舊顯著。表征異質信念的分析師預測分歧度無法解釋這一現象，意味著與Miller的理論不符，而負相關關系又與Merton的理論預測相悖，Ang等將這一異象稱為“特質波動率之謎”。

針對“特質波動率之謎”，國外的研究進行了不同的解釋。Jiang發現信息披露質量可以在很大程度上解釋特質波動率對收益率的預測效力，因為通常更少的信息披露會導致投資者之間的異質信念，從而增加股票的波動率，而信息披露越少，未來的預期收益越低，這支持了Miller的理論。Boehme等認為Merton和Miller的理論不沖突，前者是針對低“可見性”的股票，而后者對“可見性”則沒有要求，用前52周周超額收益率的標準差度量特質波動率，以機構持股度量“可見性”，在低“可見性”的股票范圍中，控制相對賣空比例，發現股票的特質波動率和預期收益顯著正相關，符合Merton的理論。Bali等則認為Ang等的結論并不穩健，使用月頻數據而非月內日頻數據估計特質波動率，使用市值加權法而非等權法構造投資組合，以及使用不同的方法分組，都會影響特質波動率與截面預期收益率之間負相關的存在性和顯著性。Fu檢驗了特質波動率的時間序列特性，發現滯后一期的特質波動率不能很好地估計下一期的特質波動率，而使用EGARCH模型估計的預期特質波動率，與期望收益率存在顯著的正相關關系；Fu還發現Ang等的結果在很大程度上受到了一部分高特質波動率的小公司的影響，這些公司在特質波動率高的月份的收益率相對更高，而在隨后的月份中則出現了負的超額收益。Huang等同樣發現控制了短期的反轉效應之后，特質波動率與預期收益率之間的顯著負相關關系消失了。

國內不少的研究發現A股市場存在特質波動率異象。楊華蔚等沿用Ang的方法估計特質波動率，發現中國市場中，股票特質波動率與橫截面收益率存在顯著的負相關關系，但與成熟市場不同，特質波動率的異常收益在小規模公司和大規模公司股票中都存在，并且換手率可以部分解釋這種負相關，他們將此解釋為市場存在的大量散戶投資者和賣空機制的缺失等交易者結構與制度限制所致。左浩苗等研究國內股票市場，同樣發現特質波動率越高，橫截面收益率越低，并且這種負相關關系與特質波動率的估計方法（GARCH、EGARCH、ARIMA模型一步向前預測的特質波動率）和組合加權方式都無關，但在控制了表征異質信念的換手率后，這種負相關關系消失了，他們將此解釋為賣空限制和投資者異質信念共同作用，導致資產被高估從而降低未來的收益率。劉維奇等、虞文微等對A股市場的研究同樣肯定了“特質波動率之謎”的存在，前者發現價格極差可以在一定程度上解釋但不能完全解釋“特質波動率之謎”，后者發現賣空機制的引入能夠降低異質信念的程度，減弱特質波動率異象。

也有研究得到了不同的結論。鄧雪春、鄭振龍發現使用ARMA模型估計得到的預期特質波動率與預期收益率之間存在顯著的正向關系，并且這種關系在考慮了各種控制變量之后依然成立。田益祥、劉鵬發現使用EGARCH（1，1）模型估計得到的預期特質波動率與股票收益率存在顯著的正相關關系，同時機構投資者持股比例越低的股票，特質風險越大，股票預期收益越高。李竹薇等基于HP濾波法將特質波動率分解為長期特質波動率和短期特質波動率兩部分，分別研究二者與股票截面收益之間的關系，發現長期特質波動率與股票截面收益成正向關系，短期特質波動率與股票截面收益成反向關系。羅登躍基于Fama-French規模-賬面市值比5×5組合對特質波動率與橫截面收益的關系進行檢驗，發現當期已實現特質波動率和非預期特質波動率均與收益顯著正相關，滯后一期的已實現特質波動率與收益的關系并不顯著，只有在控制了非預期特質波動率時，預期特質波動率才與收益顯著正相關。

以上關于特質波動率的研究主要討論了股票特質波動率與截面收益率之間的相關性，整體來看國內外都沒有形成統一的認識，原因在于研究結果與所用數據及估計特質波動率的方法有關。而另一些研究討論了特質波動率因子的表現，Mc Lean發現特質波動率越高，反轉效應越強，并且使用特質波動率作為權重能顯著提升反轉因子的效果，而動量效應與特質波動率并不相關。焦健采用規模分層提高了特質波動率因子的單調性，使得特質波動率從一個只有頭尾區分性的因子升級為具有整體單調性的優質因子。柴宗澤同樣考察了基于特質波動率的動量效應和反轉效應，發現觀察期或者持有期較長時，低特質波動率組合存在動量效應，高特質波動率組合存在反轉效應。馮佳睿、袁林青發現特質波動率因子的選股效果自發現以來并沒有減弱。

總的來看，關于特質波動率的研究多集中于特質波動率與截面收益率的關系上，而對特質波動率因子的研究較少。基于此，本文使用不同的方法、不同頻率和時間范圍的數據估計特質波動率，并從投資組合的策略表現角度，著重考慮不同估計的區別，以加深對特質波動率的理解，同時得到對投資者有參考意義的指導。

1 研究方法及數據說明

1．1 預期特質波動率的估計方法

本文采用三類不同的方法對特質波動率進行估計。

1．Fama-French三因子模型殘差的標準差

參照Ang等，將Fama-French三因子模型的殘差波動率，作為對特質波動率的估計IV1（也叫實現特質波動率）。具體地，在每個月末，對每只股票使用包括當月的最近k個月內（考慮k取1／3／6的情況）所有有交易的日度數據進行如下回歸：

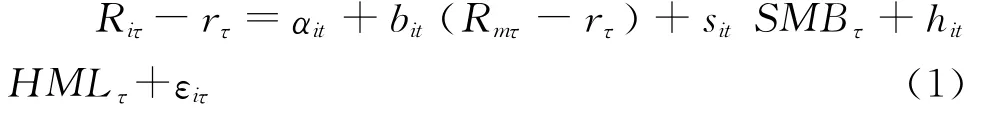
式中：i表示股票；τ表示交易日；t表示月份，τ∈t；Riτ為股票i在t月第τ日的收益率；rτ為t月第τ日的無風險收益率；Rmτ、SMBτ和HMLτ分別表示市場組合的收益率、市值因子收益率（小市值組合與大市值組合收益率之差）、賬面市值比因子收益率（高賬面市值比組合與低賬面市值比組合的收益率之差）；bit、sit和hit分別是股票超額收益率對市場組合超額收益率、市值因子收益率以及賬面市值比因子收益率的敏感系數；αit是股票i在t月的回歸的常數項，εiτ是股票i在t月第τ日的回歸殘差項。

則股票i在t月的特質波動率為

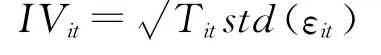
其中Tit為股票i在t月的交易天數；std（εit）為股票i在t月的殘差項序列的標準差。

2．GARCH族模型

Fu等認為，用滯后一期的實現特質波動率估計預期特質波動率，暗含特質波動率是鞅過程，對其進行單位根檢驗發現當期的特質波動率不能較好地估計下期的值，因此他們使用EGARCH（p，q）模型估計特質波動率。基于此，本文將Fama-French三因子模型作為均值方程，對日度數據或月度數據使用GARCH（1，1）和EGARCH（1，1）模型估計特質波動率。

（1）GARCH模型：若使用日度數據，對每只股票，在t月末，使用包括該月交易數據的最近k月的日度數據，估計以下GARCH（1，1）方程的系數：

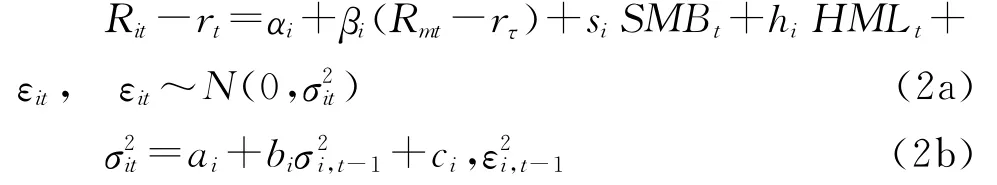
根據模型參數的估計值，將估計的σ2it序列的平均值作為對特質波動率的估計值IV2。

若使用的是最近若干月的月度數據，則將當月的波動率估計值σ2it作為對特質波動率的估計值IV2。

（2）EGARCH模型：對日度數據或月度數據，使用同上的方法估計以下EGARCH（1，1）模型，并得到估計值IV3。

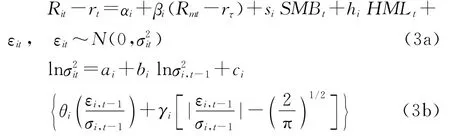
3．ARIMA模型

參考左浩苗等，本文首先估計每只股票每個月的三因素模型，得到各股票的月實現特質波動率的時間序列。t月末，使用包括t月的最近36個月的數據，對該序列采用擬合最優的ARIMA（p，q）過程（1≤p≤2，1≤q≤2，以最小AIC為標準選擇最優模型），進行一步向前預測，得到特質波動率的估計值IV4。

1．2 其他變量的選取

為對比特質波動率因子與其他因子的選股效果，本文選取以下幾個因素進行研究。

1．規模（mv）和賬面市值比（BM）。規模與賬面市值比分別代表了公司的市場特征和基本面特征。已有的研究表明，A股市場具有顯著的市值效應和賬面市值比效應。本文采用的規模變量定義為每個月月末、以億為單位的股票總市值的對數，賬面市值比定義為每個月月末、股票最新的賬面價值與總市值的比值。

2．前一個月的收益率（R-1）。Jegadeesh和Titman發現美國市場存在顯著的中期動量效應。國內股市動量效應的研究結果有所不同，朱戰宇等、周琳杰、馬超群和張浩均發現在中國市場只有形成期和持有期在4周內的周度策略中存在異常的動量收益。由此，本文以每只股票上個月末到當月月末的持有收益率衡量反轉效應。

3．換手率（turnover）。楊華蔚等、左浩苗等發現換手率可以部分解釋特質波動率與截面收益的負相關關系，而國內的研究表明換手率可以度量投資者異質性信念波動的程度（張崢和劉力），因此，本文以月換手率度量異質信念。

1．3 組合構建方法

以月為周期滾動調倉，每個月月末，在上市已滿1年的全部滬深A股中，剔除ST股票、處于停牌狀態的股票，以及當月實際交易天數不足當月總交易日的90%的股票，對剩余的股票使用當月的交易數據計算特質波動率（或其他變量）。根據計算結果將股票從低到高排序，并等分為5個投資組合，在下月第一個交易日按收盤價買入，并在最后一個交易日賣出，對買入當日漲停或停牌的股票放棄買入，賣出當日跌停或停牌的股票，延后至第一個有交易且收盤非跌停的交易日賣出，手續費按雙邊千分之三計，以等權的方式計算組合的收益率。多空組合的收益率用最低組的收益率減最高組的收益率得到。

1．4 樣本數據

本文構建組合的時間段范圍是2005年2月至2016年12月，共計143個交易月。由于某些模型估計參數需要較長時段的數據，本文所用的數據范圍包括2000年初至2016年底滬深交易所交易的所有A股的日數據和月數據，包括所有股票的上市日期，每日的后復權收盤價、交易狀態、是否ST、是否漲跌停，月末的總市值、賬面價值，每月的換手率等，以上數據來自萬德數據庫。另外，用于三因素模型回歸的Fama-French三因素日數據和月數據來源于國泰安數據庫，所用的三因素數據使用流通市值加權來構建，無風險收益率采用央行公布的三月定存基準利率折算得到。

2 實證結果

2．1 不同方法估計特質波動率所構建組合的對比

首先考慮用日度數據估計特質波動率的方法。表1給出了用不同時長的日度數據，按照不同方法估計得到的特質波動率的統計特征，IV1使用Fama-French三因子回歸殘差的標準差估計，IV2使用GARCH（1，1）模型估計，IV3使用 GARCH（1，1）模型估計，由于對GARCH族模型的估計存在不收斂的情況，IV2和IV3的樣本數都明顯少于IV1。另外，無論使用哪種方法，對特質波動率的估計值都隨著估計時間的增加而逐漸增大。

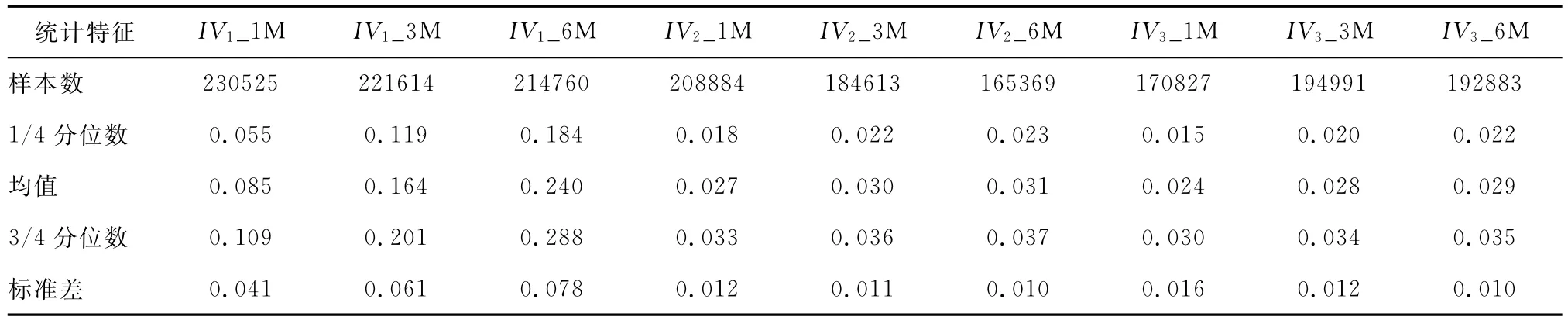
表1 使用日度數據，不同估計方法、不同估計時間得到的特質波動率的統計特征

表2給出了使用日度數據，基于不同估計特質波動率的多空策略組合的表現，包括組合月收益率的統計特征，組合的年化收益率、夏普比率、最大回撤，以及三因子回歸的截距項。在三種不同的估計方法中，對于相同的估計時間，使用Fama-French三因子回歸殘差標準差得到的組合，每期交易的股票數量最多，表現也更好：其月均收益率更高，標準差更小，正偏程度以及超額峰度都更大，年化收益率和夏普比率明顯更高，最大回撤也更小。其中，使用一個月數據估計的特質波動率組合表現最好，年化收益率高達22．06%，夏普比率達到了1．702，最大回撤僅為10．34%。另外，表2還顯示，對于同一種方法，使用的估計時間越長，得到的多空組合的表現一般越差，說明時間越遠的市場信息對投資者的指導意義越弱。

為檢驗不同估計方法對組合表現的差異是否由所交易股票樣本的不同而引起，考慮對同樣的估計時段，某只股票只有存在所有方法的估計值時，才將其列入待交易的股票池中，這一做法保證了股票樣本一致，得到的結果與表2基本一致，限于篇幅此處不再列出。

對于使用月度數據的模型，參考Fu，本文考慮使用最近60個月的月度數據估計EGARCH（1，1）、GARCH（1，1）模型，以及基于最近36個月的實現特質波動率的 ARIMA（p，q）模型（1≤p≤2，1≤q≤2）。表3給出了使用月度數據，基于不同估計特質波動率的多空策略組合的表現。可以看到，根據GARCH（1，1）和 EGARCH（1，1）模型估計的特質波動率得到的組合，除EGARCH（1，1）表現與使用日度數據估計的組合相近外，月收益率均值、年化收益率、夏普比率甚至稍小于使用日數據估計的組合，不同之處在于使用EGARCH（1，1）模型的組合的最大回撤顯著更低，不到9%。另外，使用ARIMA模型得到的組合表現介于GARCH族模型和實現波動率之間，這可能是因為部分實現波動率序列具有平穩性（鄧春雪、鄭振龍）。

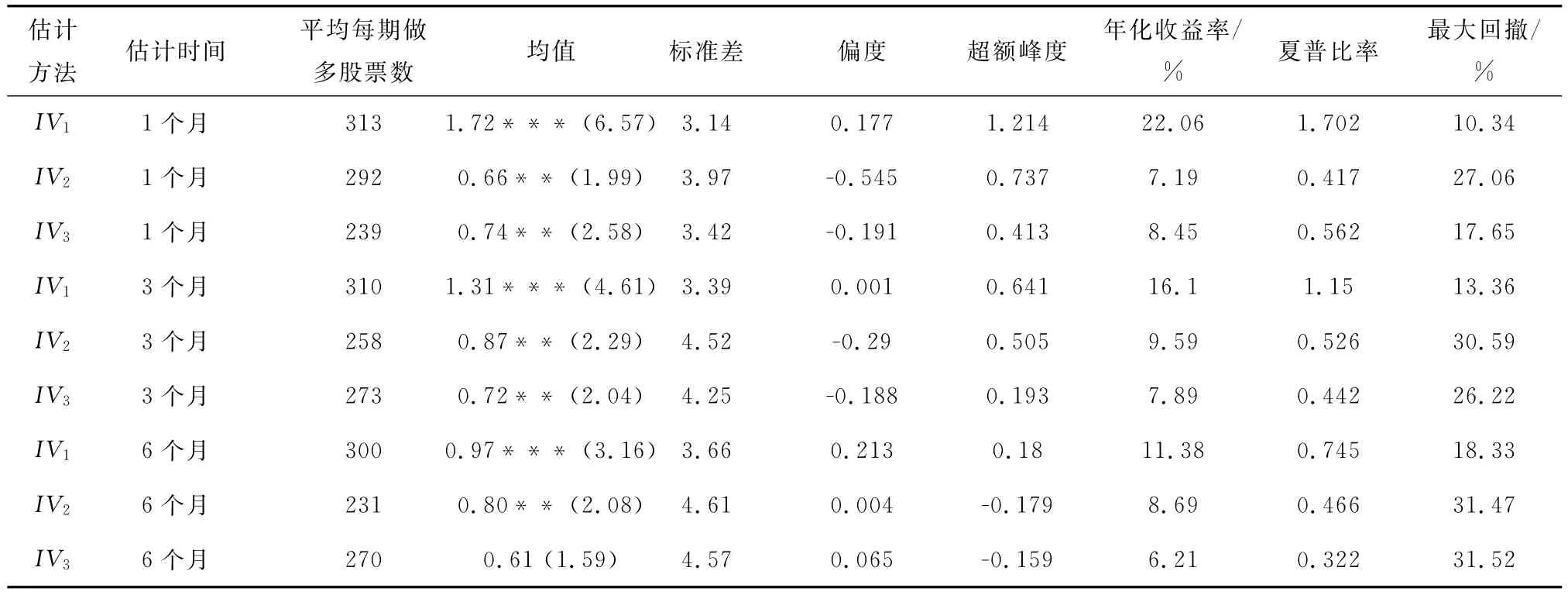
表2 使用日度數據，基于不同估計特質波動率的等權多空組合的策略表現

表4將基于實現特質波動率的多空組合，與市場組合以及基于其他分組變量形成的多空組合的表現進行對比。由該表，雖然實現特質波動率多空組合的月均收益率和年化收益率稍低于反轉組合，但它有最大的夏普比率和最小的最大回撤，整體表現最好，而市場組合的夏普比率最低。

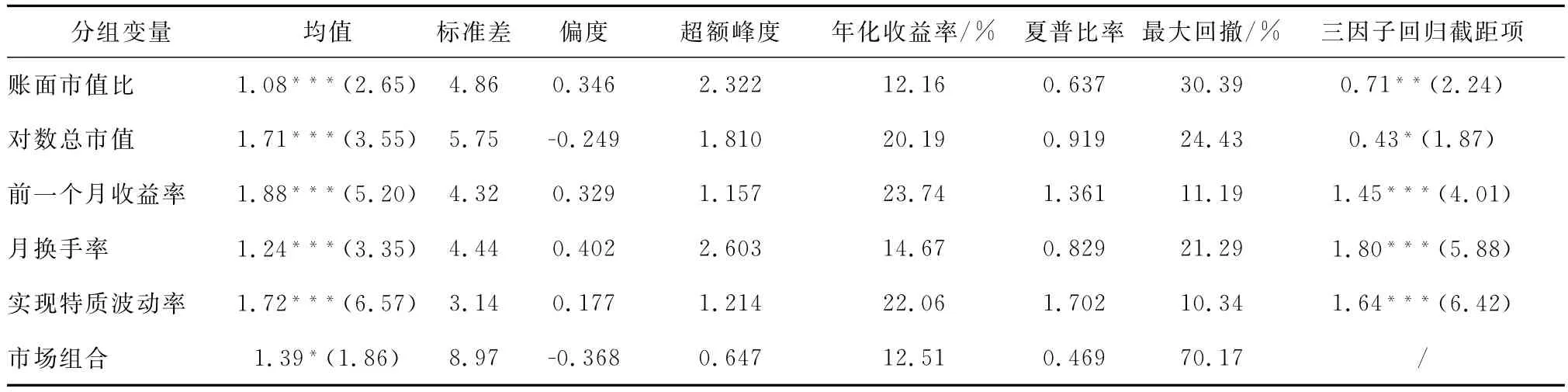
表4 單因子分組多空組合月收益率統計特征對比

2．2 根據實現特質波動率分組的各投資組合特征

以上結果表明，使用1個月的日數據估計實現特質波動率，并基于此形成的投資組合表現優于使用基于其他方法或數據估計的特質波動率的組合，也比使用其他變量形成的投資組合更好，以下考慮根據實現特質波動率分組的各投資組合特征。

表5統計了基于實現特質波動率的分組交易情況。在143個月中，每組交易的股票數量最少為163個，最多為517個，平均每月交易股票數量343個。另外，實現特質波動率越高，由于漲停或停牌無法買入，以及由于跌停或停牌賣出的情況越多。

表6統計了根據實現特質波動率分組的各組合表現。盡管各組合的夏普比率都不是很高，并且最大回撤都在50%以上，但是各組合的表現隨特質波動率的增加呈現出單調變化，均值、偏度、超額峰度、年化收益率、夏普比率都隨實現特質波動率嚴格遞減，而標準差和最大回撤隨之嚴格遞增，這說明實現特質波動率是一個好的分組變量。

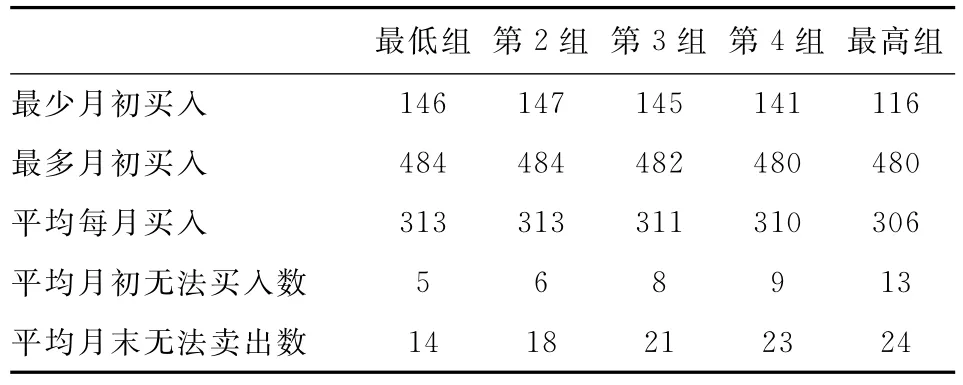
表5 根據實現特質波動率分5組，等權持倉、各組合交易股票情況

表6 根據實現特質波動率分5組，等權持倉，各組的月收益率統計特征等

表7給出了各分組組合的其他變量的平均值，由該表，實現特質波動率越高，賬面市值比、對數總市值越小，而前一月收益率和月換手率則越高，這與表8顯示的實現特質波動率多空組合的收益率與市值組合收益率負相關，與其他組合正相關一致。

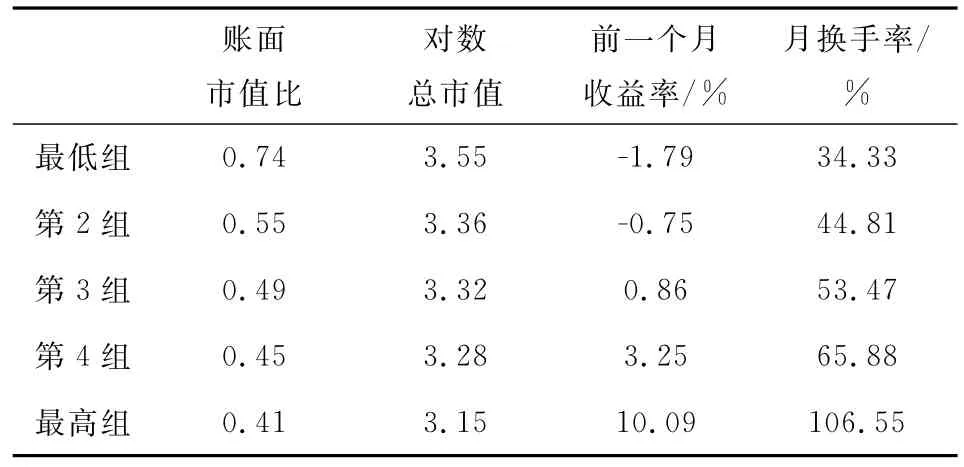
表7 根據實現特質波動率分5組，各組其他變量的平均值

表8 特質波動率多空組合與其他因子多空組合收益率相關系數

2．3 實現特質波動率多空組合的收益分解及改進

考慮實現特質波動率多空組合的收益來源，對多空組合月收益率進行多因子回歸，表9給出了多元回歸分析的結果，其中R＿M、SMB、HML分別為市場因子、市值因子、賬面市值比因子，MOM、TUR分別表示參照Fama、French構建的動量因子和換手率因子。由該表，三因子模型下，截距項顯著為正，組合市場收益率顯著負相關，與市值因子的關系不顯著，與賬面市值比顯著正相關且系數較大。單獨加入動量因子或者換手率因子會降低截距及市場因子的絕對值和顯著性，提高賬面市值比的顯著性并大幅增加調整后的R2，加入換手率因子后，市場因子的影響不再顯著，而市值因子的影響則變為正顯著，模型的解釋力大幅提高。包含所有因子的模型中，系數及顯著性從大到小依次為換手率、賬面市值比、反轉、截距項，市場因子則不再顯著。這些結果與左浩苗等所發現的，在控制換手率之后，特質波動率與截面預期收益率之間的關系不再顯著一致，說明特質波動率在一定程度上可以表征異質信念。

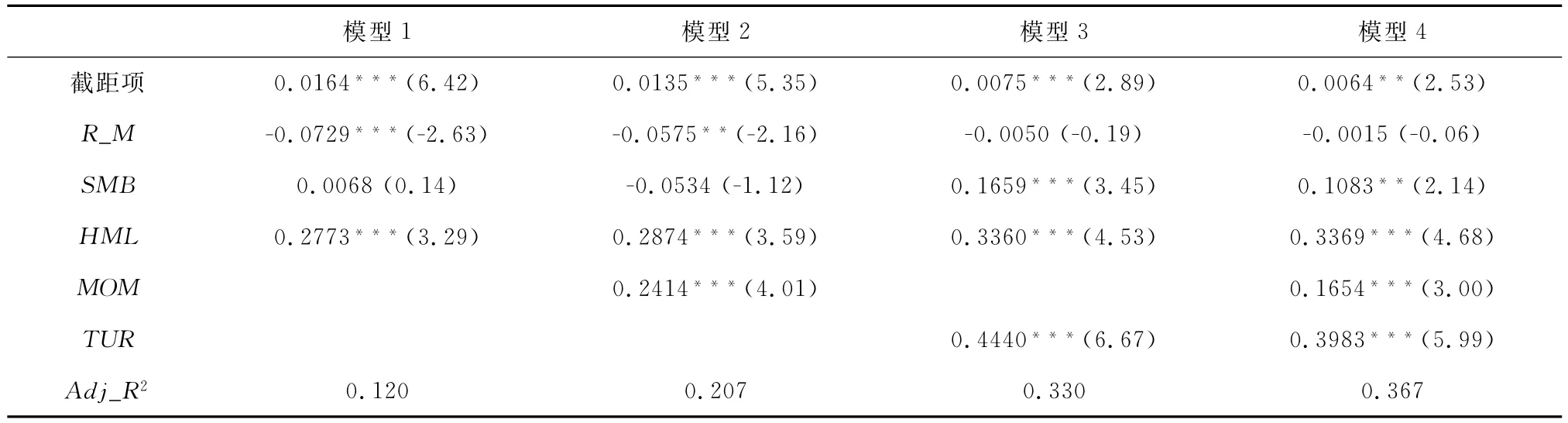
表9 實現特質波動率多空組合月收益率的回歸分析

表9的模型1說明實現特質波動率多空組合的收益率與市場因子顯著負相關，由此，實際中可以考慮利用市場組合進行對沖。簡單起見，每個月末使用未對沖的組合最近12個月內的日數據，估計組合的β系數，對沖組合的收益率用原始組合收益率減去β與市場收益率之積。由于需要12個月的時間估計，對沖組合共有131個交易月。由表10，相比未對沖的組合，對沖組合的月均、年化收益率以及夏普比率都有所提高，最大回撤、收益率標準差、超額峰度等相差不大。圖1也直觀地反映了對沖組合的表現確實穩定地優于未對沖組合。

表10 對沖與未對沖的多空組合對比

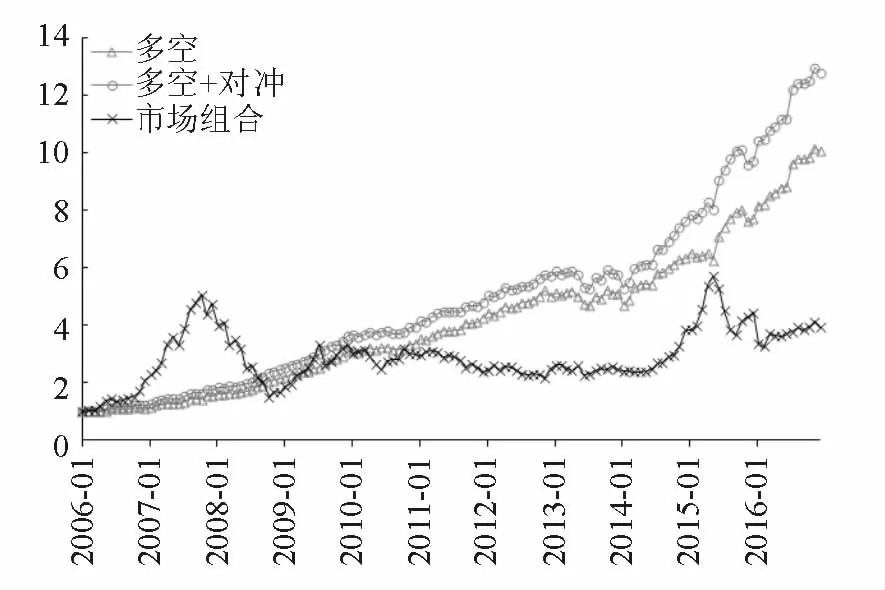
圖1 對沖、未對沖組合與市場組合的對比

3 小結

本文首先使用三因子模型回歸殘差波動率、EGARCH（1，1）、GARCH（1，1）以及 ARIMA 等不同估計方法，基于不同頻率或時段的數據估計特質波動率，進一步構造多空組合，對比發現使用Ang等提出的三因子殘差波動率（實現特質波動率），基于1個月的日度數據估計的特質波動率，得到的投資組合的表現顯著優于其他方法得到的組合，而GARCH族模型估計的特質波動率構造的多空組合表現一般，但是其年化收益率多數為正，這支持了左浩苗等的結論，并與田益祥、劉鵬等人的結果相反。同時，該組合也優于使用賬面市值比、市值、前1個月收益率、換手率等指標分組構建的多空組合。

對基于實現特質波動率的組合分組統計，發現特質波動率越高，賬面市值比、市值越小，前期收益率及換手率越高，組合收益率與市值因子負相關，與其他因子正相關。進一步對月回歸進行分析，可知換手率因子對組合收益率的解釋力最大，這與國內已有的研究一致，說明特質波動率因子的收益率可以由異質信念解釋。