CrI3高壓相變及其光學性質理論研究

張麗琴, 袁五屆, 張金峰, 徐士濤

(淮北師范大學信息學院， 淮北 235000)

1 引 言

伴隨著碳六元環組成的石墨烯被Geim小組[1]成功分離，二維材料在電學[2]、磁學[4,5]、光學[6,7]、熱學[8]等方面所展示出來的獨特魅力，引起科學家的關注. 隨著科學家在理論研究和應用領域的不斷探索及深入研究，越來越多的二維材料被相繼找到. 如過渡金屬硫族化物(TMDS)[9-11]，其體材料具有間接能隙，單層變成直接能隙半導體且價帶劈裂成兩個自旋極化的能帶；同時通過施加極化強光，發現單層具有劇烈的光吸收現象. 他們獨特的電子結構和光學性質使其在光電子器件上具有非常廣泛的應用前景[12-28]. 進一步的研究發現，單層黑鱗具有各項異性的能帶結構[14, 15]. 更加奇異的是，隨著層數的增加，帶隙變的連續可調[18, 19]，這個使其在低維壓電材料中的應用成為可能. 隨著維度的減小[17,24]，單層二硫化鉬(MoS2)在層間耦合效應消失的同時[25,27]，其體相也由間接帶隙半導體變成單層的直接帶隙半導體且谷自旋效應得以實現[21,29].

然而，大多數二維材料，包括石墨烯等，都不具有本征鐵磁性. 盡管可以通過磁原子摻雜和磁近鄰效應等方法引入鐵磁性，但在二維半導體中實現長程有序的自旋排列面臨巨大挑戰. 兩維的CrI3是非常罕見的本征鐵磁半導體[29,30]. 徐曉棟教授和他的合作團隊從實驗上論證了CrI3隨著層數的不同，展現出跟體相完全迥異的物理性質. 實驗證實，單層的CrI3成為具有面外自旋取向的Ising鐵磁體. 雙層CrI3所展現出的磁性受到了抑制，而三層CrI3則顯示，其被抑制的鐵磁性得到了修復. 這使得兩維CrI3在磁傳感器以及信息存貯方面有著極大的應用前景. 理論上，zhang等人[27]詳細研究了體相下CrI3的磁性及其光學性質. 并進一步驗證單層CrI3的電子、光學和磁性性質. 然而，到目前為止，理論上鮮少涉及體相材料CrI3結構及其光學性質. 本文基于第一性原理的理論計算，對體相材料CrI3的上述性質進行了詳細的分析.

2 基本理論和方法

在本文中，利用基于密度泛函理論的第一性原理平面波軟件包CASTEP計算體相CrI3極性條件下及電子性質和光學性質[31,32]. 采用Perdew-Burke-Emzerhof(PBE)作為交換關聯泛函，用綴加投影贗勢波描述離子實和價電子間的相互作用[33]. 采用廣義梯度近似(GGA)的PBE泛函處理電子之間的相互交換關聯作用.

首先，計算不同壓強下體相CrI3的電子性質和光學性質. 在計算過程中選取截斷能為750 eV，布里淵區K點網格為9×8×8. 其次，計算的平面波基組采用700 eV截斷能，布里淵區K點的積分網絡由Monkhorst-Pack形式產生,總能量的收斂精度為10-5eV. 結構優化和計算的網絡分別為3×3×1和9×9×1.

3 結果與討論

3.1 體相CrI3的幾何結構和穩定性

3.2 體相CrI3的能帶密度結構

在不考慮電子自旋的情況下，通過廣義梯度近似計算(GGA)得到體相CrI3的能帶結構，如圖1所示，從圖中可以清晰的看出，在零壓常溫下得到的禁帶寬度為3.204 eV,遠遠高于Dillon團隊[35]于1964年所測量的實驗值1.2 eV. 實驗值跟理論值出現了接近三倍的偏差，究其原因，一是CrI3是一種磁性材料半導體，沒有考慮其自旋. 二是因為Cr原子含有d軌道，存在較強的旋軌耦合和強關聯，沒有加入U. 考慮到電子的自旋及其存在的d軌道而導致的強關聯耦合，得到如圖2所示. 從圖中可以看出，CrI3的禁帶寬度是1.09 eV的半導體，與已經存在的實驗值非常接近. 結合圖3的能態密度圖，可以看出，在Fermi能級附近，參與軌道成鍵的主要來自于I的p軌道和Cr的4d軌道. Cr的4d軌道能帶寬度比較大，說明Cr 4d軌道參與了成鍵. 同理，I的5p軌道在Fermi能級附近參與了成鍵. 在Fermi能級附近，I的5p軌道和Cr 4d軌道能帶較寬且態密度的峰值比較尖銳，說明在這些位置，離域性強且存在較強的軌道自旋耦合. 因為帶越寬，成鍵越強，態密度峰跨度越大，離域性越強，成鍵越強，軌道自旋耦合越強. 考慮到包利不相容原理，I的5p軌道由于存在較大的電負性而Cr 4d軌道金屬部分容易失去電子而對原子軌道的貢獻較少. 考慮到電子的自旋以及軌道耦合，可知隨著成鍵作用的加強，成鍵分子軌道下移而反鍵分子軌道上移. 自旋向上的原子的成鍵軌道下移而自旋向下的反鍵原子軌道上移，導致能帶變窄.

圖1 零壓下不考慮電子自旋及其關聯耦合時的能帶圖Fig. 1 Energy band diagrams at zero pressure without considering electron spin and associated coupling

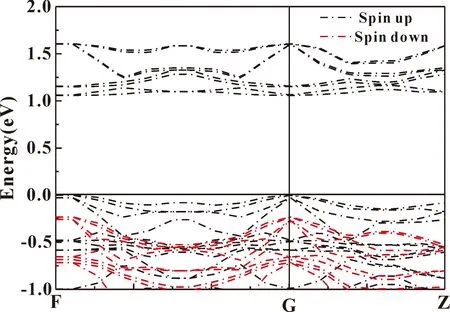
圖2 零壓下考慮電子自旋及其關聯耦合的能帶圖Fig. 2 Energy band diagrams at zero pressure considering electron spin and associated coupling

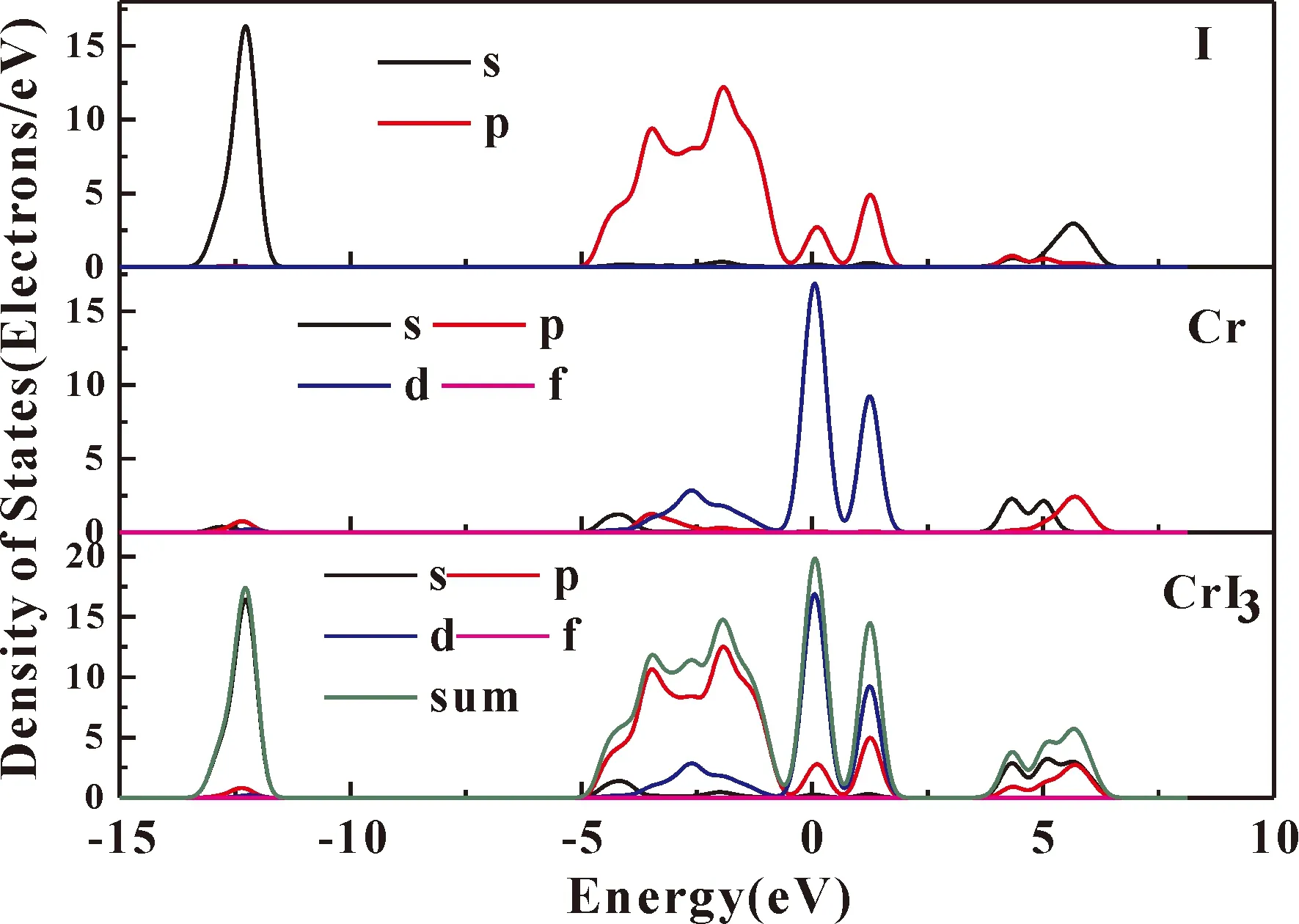
圖3 零壓下CrI3態密度圖Fig. 3 Density of states of CrI3 at zero pressure

圖4 P=26.1 GPa CrI3的能帶圖Fig. 4 Energy band diagrams at pressure 26.1 GPa of CrI3 considering electron spin and associated coupling

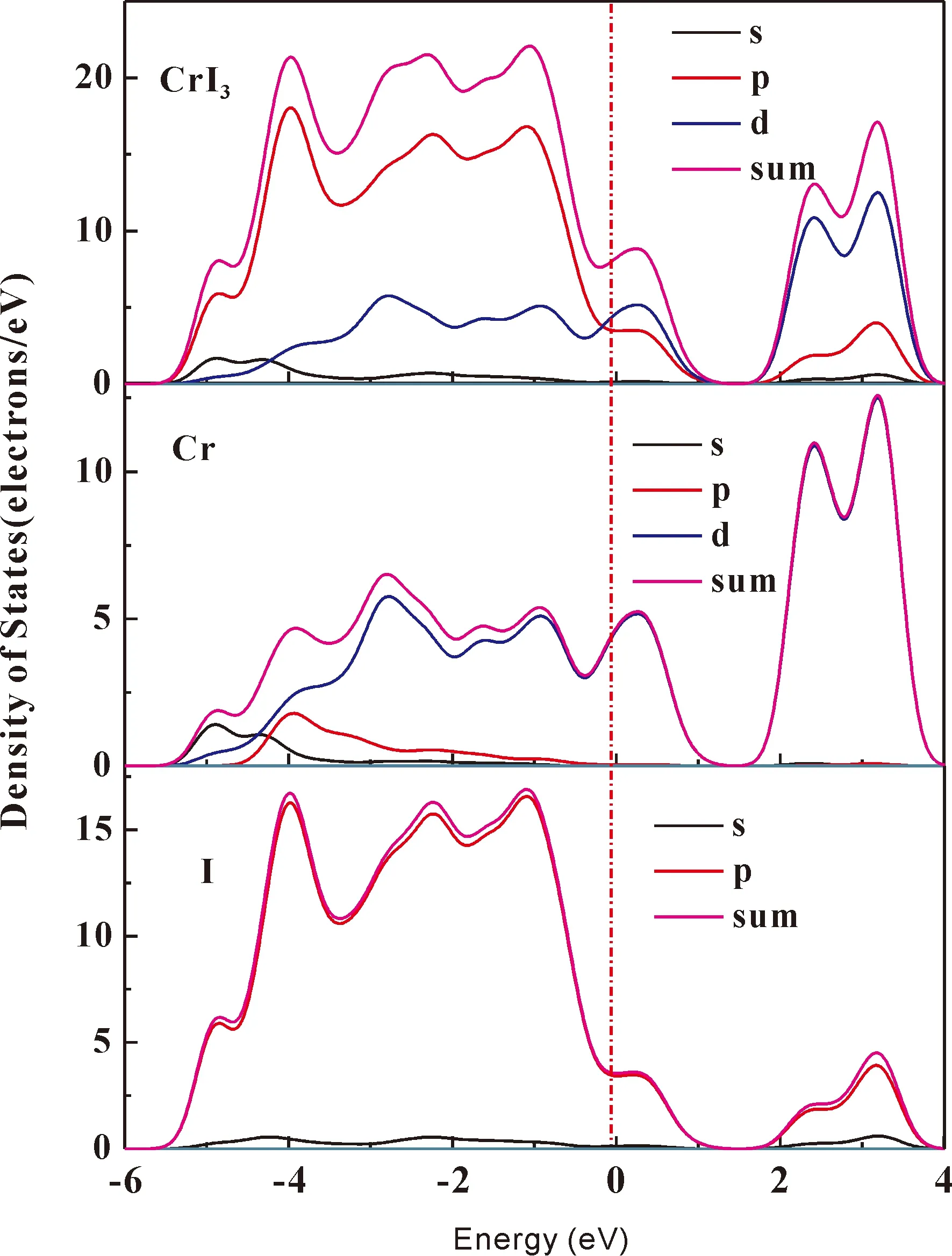
圖5 P=26.1 GPa CrI3的態密度圖Fig. 5 Density of state diagrams of CrI3 at pressure 26.1 GPa considering electron spin and associated coupling

3.3 體相CrI3的差分電荷密度

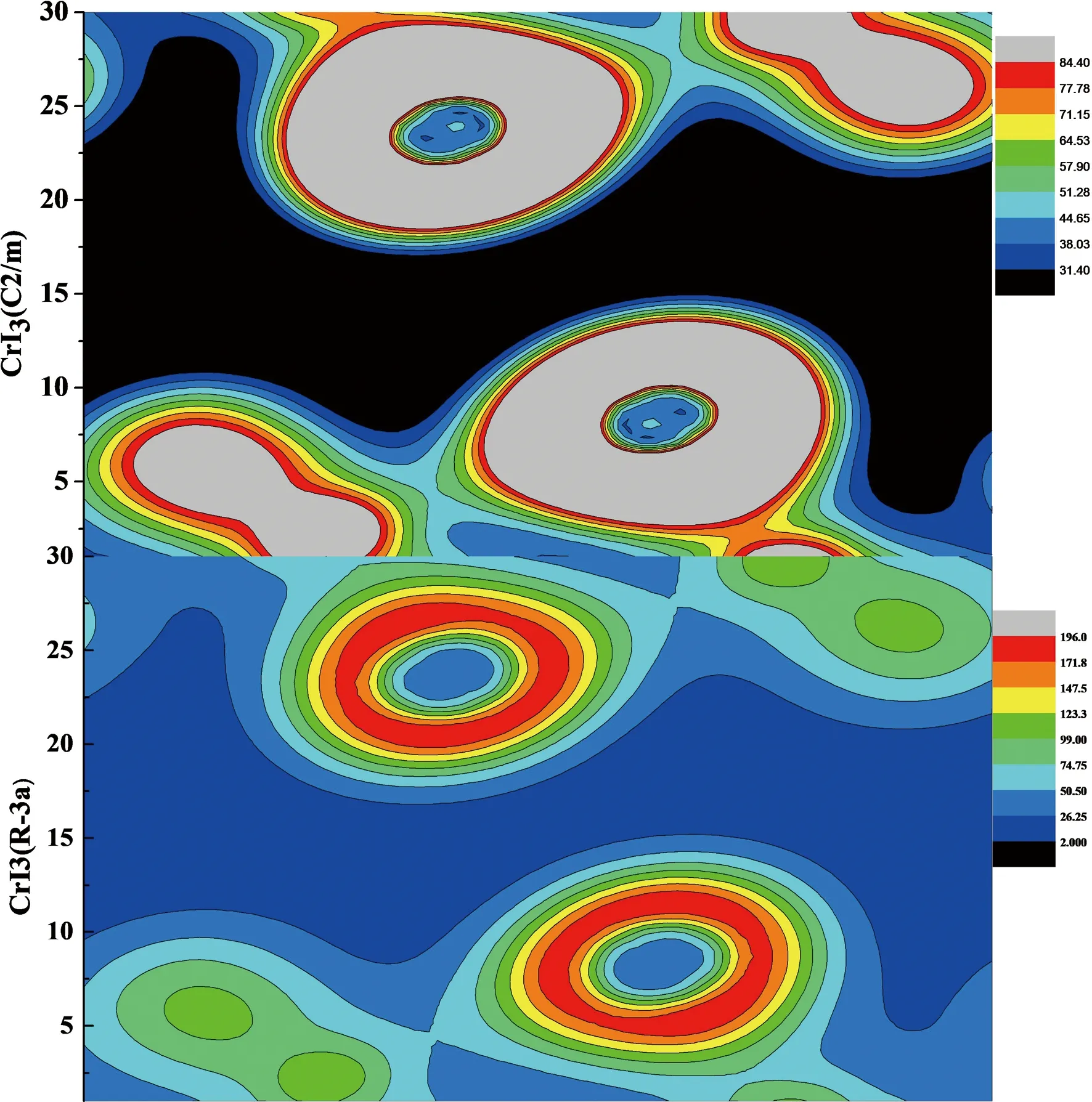
圖 6 體相CrI3分別在到C2/m相是的差分電荷密度圖Fig. 6 Differential charge density diagram of CrI3 at phase and phase C2/m

3.4 體相CrI3的光學性質

物質的光學性質對研究其在光學成像，光學器件的制備，傳感技術，機械工程技術方面有舉足輕重的作用. 在光電子物理、凝聚態光譜、半導體光電子物理已經得到廣泛的應用. 本文通過計算體相CrI3的吸收譜、介電函數、反射譜、損失函數等光學性質來進一步了解其物理性質. 利用能帶結構，躍遷矩陣和電子態密度，可以推導得到介電函數的實部、虛部、折射率、吸收系數、消光系數等. 利用Kramas-Kronig關系，得到關于介電函數的實部和虛部之間的關系.

f(kn)×(1-f(kn′)δ(Ekn-Ekn′-?ω)

(1)

(2)

其中，n和n′分別表示導帶和價帶,f(kn)為第一布里淵區的動量矩陣元，根據公式[1]和[2]我們可以得到吸收系數、折射率和消光系數.

吸收系數

(3)

折射率

(4)

消光系數

(5)

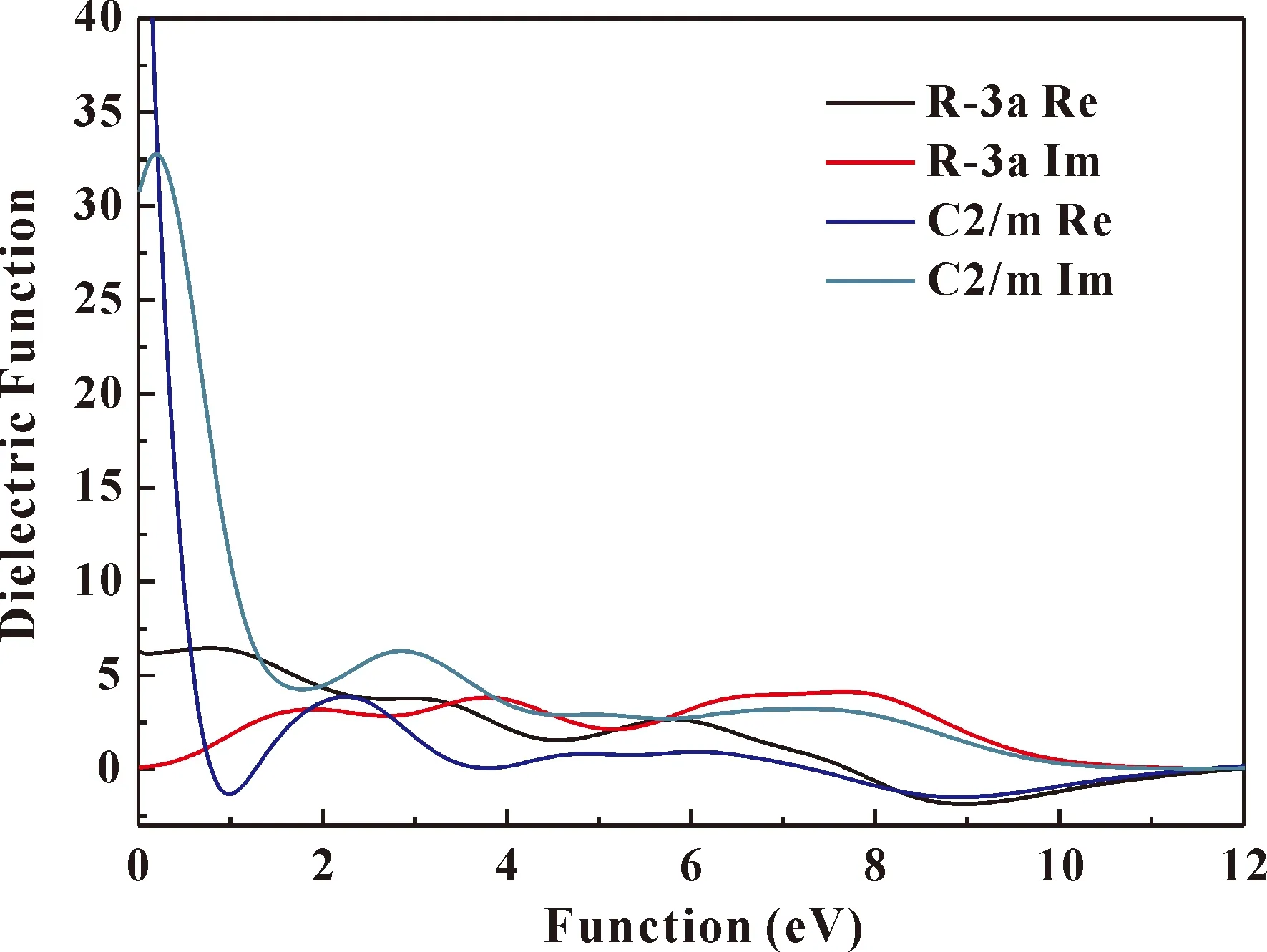
圖 7 體相CrI3分別在到C2/m相時的介電函數Fig. 7 Dielectric functions of CrI3 at structural and C2/m respectively

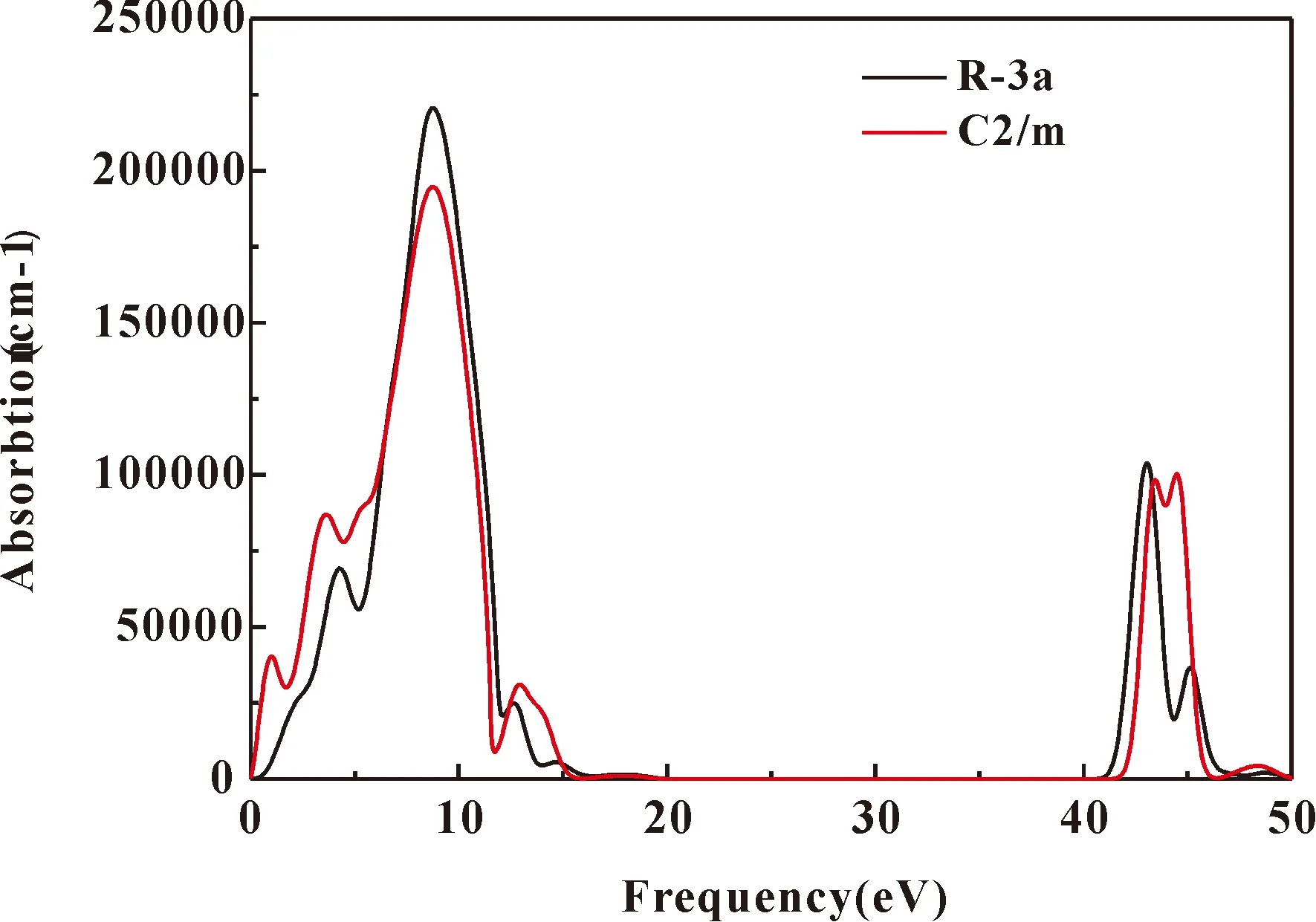
圖 8 體相CrI3分別在到C2/m相時的吸收譜Fig. 8 Absorption spectra of CrI3 at structural a and C2/m respectively

折射率和消光系數分別來源于復折射率的實部(n)和虛部(k)，折射光譜、消光光譜在近紅外區域電子躍遷非常活躍. 可見區域2.0 eV-5.0 eV附近，電子的折射光譜與消光光譜都對應一個相當寬的頻率區間. 復折射率的實部(n)在虛部(k)上升和下降的斜率處分別出現了極值，這與其譜線的峰值較多是相對應的，均由于體相CrI3能帶結構彌散性相比較強引起的變化.

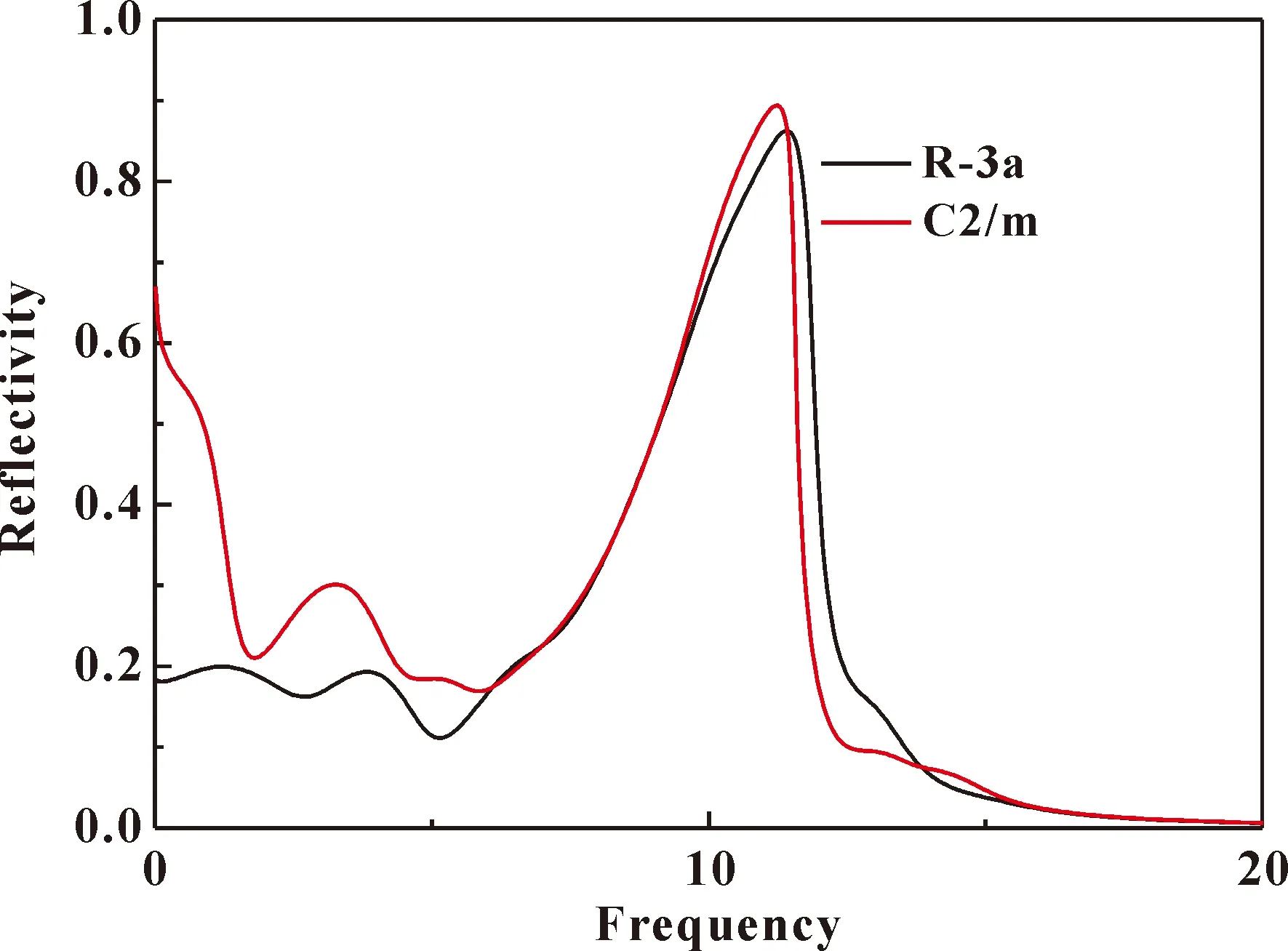
圖9 體相CrI3分別在到C2/m相時的反射譜Fig. 9 Reflectivity spectra of CrI3 at structural and C2/m respectively

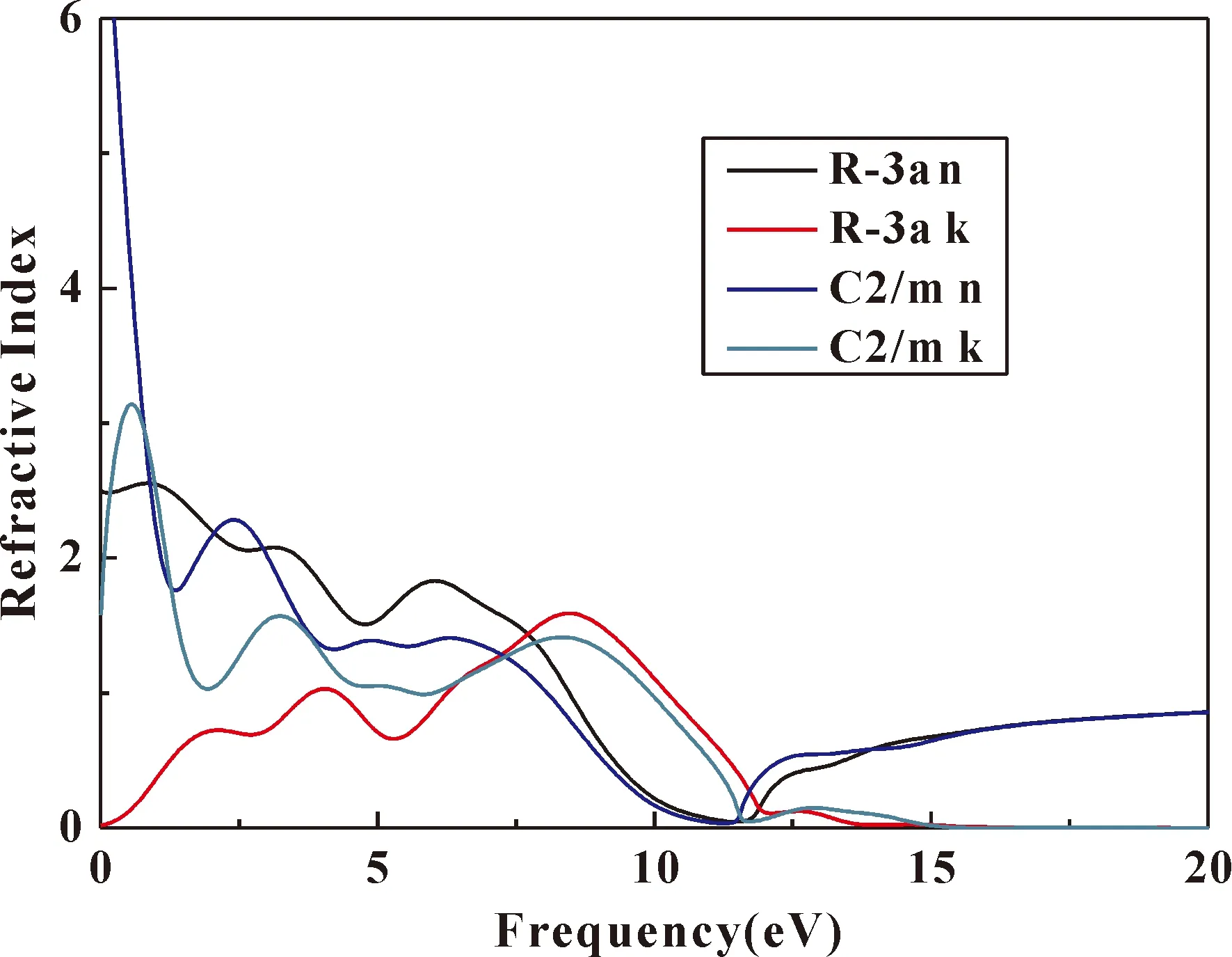
圖10 體相CrI3分別在到C2/m相時的折射譜Fig. 10 Reflective index of CrI3 at structural and C2/m respectively

4 結 論