鈾氫化反應過程中氫擴散行為的第一性原理研究

賓 韌， 王 鑫， 敖冰云， 汪小琳

( 1.表面物理與化學重點實驗室，江油 621908； 2.中國工程物理研究院材料研究所，江油 621907； 3. 中國工程物理研究院，綿陽621900 )

1 引 言

鈾的氫化腐蝕以其快速反應和對材料的顯著破壞而備受研究者們關注. 而極高的化學活性使得金屬鈾表面不可避免存在由氧化物及吸附雜質構成的表面層，從而導致了鈾氫化反應行為非常復雜. 表面層的狀態如氧化層厚度及特性、表面吸附雜質種類和濃度、表面粗糙度、機械加工導致的殘余應力等，都影響著氫化反應的成核機制及動力學特征[1].

鈾氫化反應可分為四個階段：(1)孕育期. 其主要原因是反應初期氫需擴散通過表面層，在界面處累積到臨界濃度才能生成氫化物. 氧化層的厚度決定了氫在其中擴散到達界面并達到足夠濃度所需要的時間[2]. (2)線性生長階段. 孕育期結束后，氫化物發生局部形核并開始生長. 這一階段由于表面層及金屬基體的不均勻性，氫化物形核位點具有離散且分布不均勻的特性[3]. 但單個氫化物核的尺寸增長速率近似為線性，而整體氫化反應速率曲線呈S型. (3)體相反應階段. 這一階段各氫化物形核點相互連接并完全覆蓋金屬表面，這也意味著表面氧化層的完全破壞. 此時反應速率達到最大值且近似不變，反應由氫化物-金屬界面的性質控制[4]. (4)終止階段. 這一階段反應物耗盡，反應速率逐漸降低直至終止.

從微觀上看，在鈾氫化反應過程中涉及的介質及其主要作用有：

(1)鈾氧化物. 研究表明，UO2表面氫分子吸附的粘滯系數約6×10-4，氫原子在UO2晶格中溶解度僅為7×103cm-3，而擴散勢壘達57-60 kJ·mol-1[5, 6]，這使其在氫化反應過程中起到擴散阻擋層的作用，其厚度影響孕育期和初期成核速率[7].

(2)金屬鈾. U與H2的反應在能量上是有利的，因此反應速率主要由動力學因素決定. 氫在U晶格中的飽和溶解度僅為5×1017cm-3[8]，遠小于生成氫化物所需的臨界氫濃度(1.4×1023cm-3)，這導致氫不可能在鈾表面均勻反應，而是在晶界、第二相界面等處優先聚集到足夠濃度才能形核[9, 10].

(3)鈾氫化物. 在氫化反應的體相階段，反應生成的UH3成為阻隔H2與金屬基體的唯一介質. 但與氧化物不同的是，疏松的UH3不僅不能阻止反應，反而對氫化反應起到促進作用，反應速率在體相階段達到最大值. 目前氫在UH3晶格中的溶解與擴散行為仍沒有定量研究數據.

為研究鈾的氫化反應動力學及產物特性，筆者在其表面沉積一層相對惰性的金屬Pd，以促進氫的解離吸附、阻擋表面生成氧化層并降低雜質氣體的吸附，因此鈾的氫化反應不存在孕育期. Pd對H2具有較高的選擇透過性，且其氫化物PdHx(x=0.6～0.7)中氫原子密度達43 nm-3，更易達到β-UH3的成核的臨界氫濃度(82 nm-3)，因此氫化反應后在Pd膜下生成了厚達數個微米的均勻層狀α-UH3.α-UH3只能在低溫、低壓、惰性氣體稀釋下緩慢反應生成[11-13]，而通常條件下鈾氫反應產物幾乎全部為β-UH3. 在沉積Pd的條件下，反應初期氫化速率在較長時間內保持恒定；而在反應后期Pd膜破裂后氫化反應速率明顯上升. 這表明與通常氫化反應體相階段相比，Pd膜的存在導致氫化反應的速率受到了限制，導致反應產物主要為α-UH3.α-UH3被認為是亞穩態，或者氫化反應過渡產物，長時間加熱將不可逆地轉化成β-UH3. 事實上，α-UH3與β-UH3具有相似的結構和密度，兩者的形成能非常接近[14]，實驗測得的生成焓差異小于量熱裝置的誤差[15]. 因此鈾氫化反應產物的選擇性，主要由動力學因素控制，即主要涉及氫在上述介質中溶解、擴散過程.

然而，對鈾氫化反應動力學特性及產物選擇性的研究，難以在實驗上深入到微觀層次. 這是因為鈾及其氫化反應產物均具有非常高的化學活性，在制備和分析過程中會發生嚴重的氧化；通過實驗制備的α-UH3不可避免地混有大量的β-UH3，且無法有效的分離，也對α-UH3相關性質的實驗研究帶來困難. 采用理論計算可以模擬微觀尺度上氫化反應的發生過程，是對實驗研究的有力補充. 但以往對U-H體系的理論研究報道多以氫化物基態性質和氫原子的靜態性質為主[16-18]，缺乏動力學相關的詳細報道，因此，本文利用第一性原理計算方法，嘗試從微觀上分析氫在UO2、PdHx及兩種氫化產物α-UH3、β-UH3中固溶、擴散的行為，來研究不同表面狀態下氫化反應動力學特性，以期解釋Pd膜作用下氫化反應產物具有選擇性的原因.

2 計算方法和模型

本文用于實現密度泛函計算的程序為VASP (Vienna Ab-initio Simulation Package)[19]，采用基于廣義梯度近似 (GGA)的Perdew-Burke-Ernzerhof泛函[20]，所選取的贗勢也對應為采用投影綴加平面波方法構建的PAW-PBE贗勢，涉及元素選用的價電子態為U 5f36s26p66d17s2，Pd 4s24p64d10，O 2s22p4，H 1s1. 經收斂性測試，截斷能統一設定為600 eV，并采用足夠的k網格密度(0.05 ?-1)以保證能量收斂到10-5eV. 在晶體結構弛豫方面采用精度逐漸提高的分步優化方法，即先采用共軛梯度(CG)方法對晶格進行初步優化，再用精度更高的擬牛頓(RMM-DIIS)方法進行進一步的結構優化，直到所有原子的受力收斂到0.001 eV/?-1，然后采用Bl?ch修正的四面體方法進行靜態計算. 考慮到U-H體系具有磁性，在計算時考慮自旋極化，并確定α-UH3和β-UH3的基態磁性質.

對氫原子在材料中的擴散路徑和擴散勢壘的相關計算是利用Henkelman小組開發的VTST(Transition State Tools for VASP)程序包提供的CI-NEB(Climbing image nudged elastic band)方法來實現. 它通過確定兩個能量最低的摻雜構型作為初態或終態(可能是能量相同的等效構型)，設計可能的擴散路徑，再使用CI-NEB方法計算擴散路徑中原子逐漸運動的一系列構型的能量、受力情況，所獲得能量最高的點確定為擴散路徑中的過渡態. 弛豫后得到的一系列中間構型即為擴散過程中的最小能量路徑(minimum energy path, MEP)，過渡態與基態(初始態或終態)之間的能量差即為擴散勢壘. 由于摻雜構型的體系較大且對稱性較差，對擴散路徑中各鏡像的計算精度稍有降低(k點網格密度0.1 ?-1，受力收斂到0.01 eV/ A-1). 獲得鞍點構型后，為了進一步提高過渡態的結構和能量精度，再利用Dimer方法在該構型附近進行更精細的過渡態結構搜索[21, 22]. 另外，對原子構型文件的編輯處理及相關圖像繪制均利用免費軟件VESTA[23]完成并輸出.

3 結果及討論

3.1 氫化物晶體結構

α-UH3和β-UH3均具有Pm-3m(223)的空間構型，但兩者的原子占位不同. 兩種氫化物的晶體構型如圖1所示. 在α-UH3單胞中有兩個U原子和6個H原子，分別占據Wyckoff 2(a) (0, 0, 0)和6(d) (1/4, 0, 1/2)位置；而在β-UH3單胞中，8個U原子分為兩組(UI和UII，如圖1b所示)，分別占據了2(a)和6(d)的格點(對應α-UH3中U、H原子的位置)，而24個氫原子占據了24(k) (0, 0.156, 0.313)位置[24]. 可以看出，α相和β相中，所有U原子均處于12個氫原子組成的二十面體籠中，U-H距離均為2.31 ?[25].

圖1 α-UH3和β-UH3的晶體結構Fig. 1 Crystal lattice structures of α-UH3 and β-UH3

3.2 兩種氫化物形成能的計算

衡量通常狀態下兩種氫化物相之間穩定性差異，最直接的方法是比較兩者的形成能ΔEf(Energy of Formation)，對氫化反應

(1)

定義UH3的形成能ΔEf

(2)

即生成物總能減去生成該物質所需的反應物總能之和. 與鑭系元素類似[26, 27]，在計算時也要考慮磁性的貢獻. 表1列出了計算得到的α-UH3、β-UH3的晶格常數和形成能，作為對比還計算了α-U的晶格常數、UO2的晶格常數及形成能，并與實驗值對照.

表1α-U、α-UH3、β-UH3和UO2等物質的晶格常數及形成能

Table 1 Calculatedand experimental lattice constants and energy of formation forα-U,α-UH3,β-UH3and UO2

Lattice constant (?)Energy of formation (eV)CalculatedExperimentCalculatedExperimentα-Ua=2.805b=5.844c=4.902a=2.844,b=5.869,c=4.932 [28]--α-UH3a=4.123 (FM*)a=4.038 (NM*)a=4.161[11]-1.073 (FM)-0.756 (NM)-β-UH3a=6.590 (FM)a=6.464 (NM)a=6.631 [24]-1.093 (FM)-0.769 (NM)-1.190[29]UO2a=5.416a=5.471 [30]-10.782-10.650[31]

*FM：ferromagnetic，NM：non-magnetic

由表1可以看出，考慮了自旋極化后，α-UH3、β-UH3的基態均具有鐵磁性，其晶格常數、形成能的計算值與實驗值均符合較好. 雖然α-UH3的生成焓略高于β-UH3，被認為是亞穩態，但計算結果表明它們之間生成焓的差異非常小，只有0.020 eV/atom U (2.03 kJ·mol-1). 單純從熱力學穩定性差異來解釋α-UH3產量遠少于β-UH3這一現象并不充分. 下面我們建立氫原子在α-UH3、β-UH3、UO2和PdHx中摻雜的模型，比較不同濃度下摻雜的溶解能，并計算摻雜原子在間隙中擴散的勢壘.

3.3 摻雜體系的溶解能

氫原子自身體積非常小，在晶格中一般以填隙固溶的方式存在，對晶格中所填充的間隙位而言，它的優先占據首先必須考慮間隙的大小. 由于α-UH3和β-UH3晶格中的鈾原子均與最近鄰的氫原子構成了UH12正二十面體，氫原子較易進入這些正二十面體之間的間隙. 如圖2所示，這樣的間隙一共有三種，分別為α-UH3(0, 1/4, 1/2)、β-UH3(0, 1/4, 1/2)和β-UH3(1/4, 1/4, 1/4)，這些間隙均由氫原子構成，間隙內氫原子并不會與鈾原子直接接觸.

圖2 氫化物晶格中的幾種間隙Fig. 2 Interstitials in α-UH3 and β-UH3 lattices

不考慮摻入氫原子后引起的晶格畸變，這些間隙中心與最近鄰的氫原子之間的距離分別為1.47 ?、1.39 ?、1.82?，均顯著大于氫原子半徑，這表明這些間隙可能具有容納多個氫原子的能力. 近期研究者們通過理論和實驗研究發現，類似LaH10[32]，在加壓的情況下鈾與氫可形成一系列的化合物且可能具有超導特性[33, 34].

不考慮溫度和壓力條件，氫化物中氫原子的溶解能為

(3)

其中Eintrinsic和Edoped為摻雜前后氫化物晶胞的能量(均充分弛豫)，EH2為孤立氫分子能量，n為晶格中摻入的H原子數目，m為所計算晶胞中U的數量. 為得出溶解能隨摻雜濃度的變化趨勢，選取α-UH3的2×2×1超晶胞及β-UH3單胞，依次向對應間隙填充氫原子，對這些摻雜構型進行計算得出該間隙氫的溶解能. 為使摻雜體系能量最低，插入的氫原子兩兩之間盡可能遠、且對稱性盡可能高. 計算結果如圖3所示. 作為對比圖中也給出了UO2晶格中氫原子的溶解能變化.

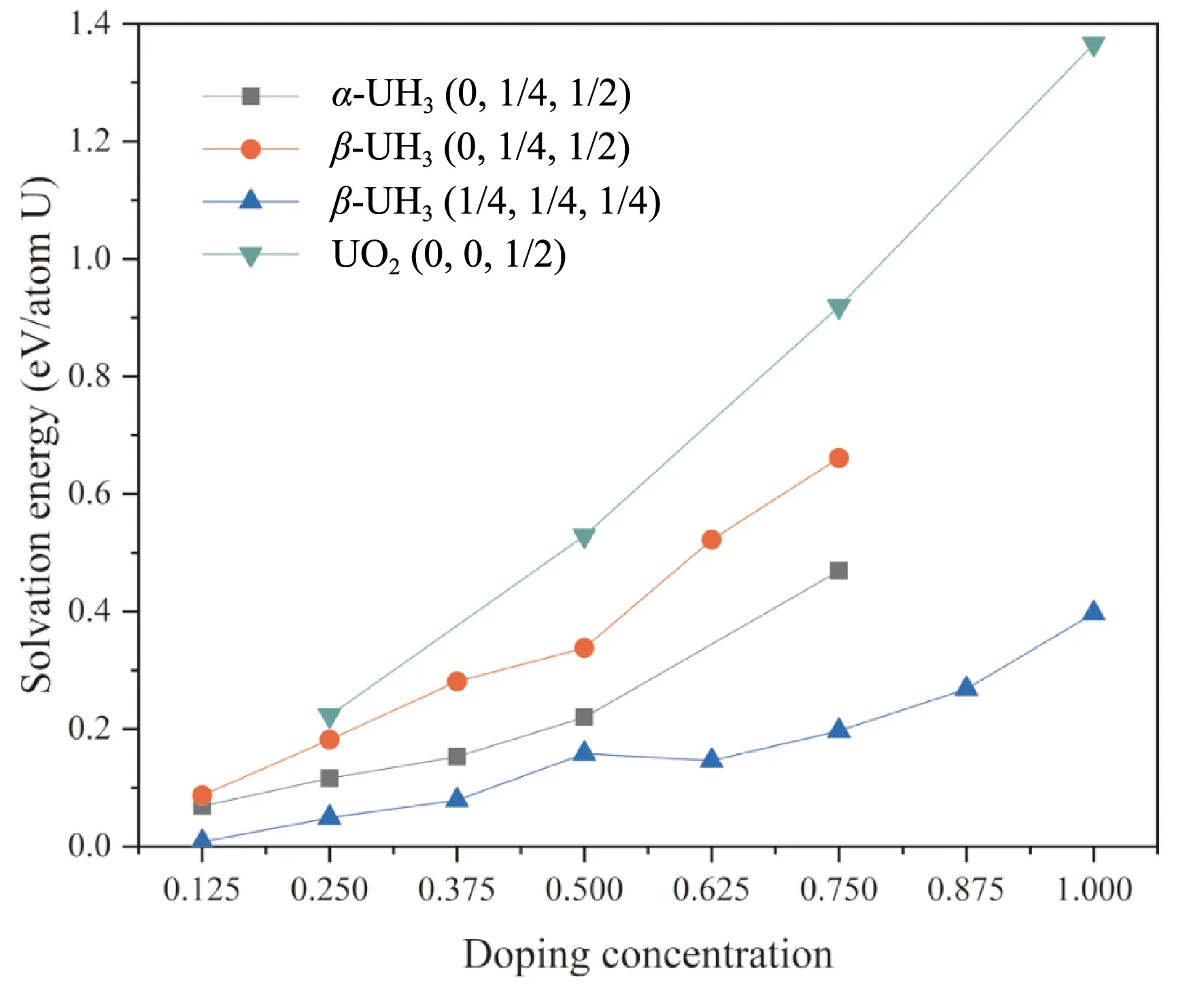
圖3 α-UH3(0, 1/4, 1/2)、β- UH3(0, 1/4, 1/2)、β- UH3(1/4, 1/4, 1/4) 及UO2(0, 0, 1/2)三種間隙氫原子溶解能隨摻雜濃度的變化Fig. 3 Energies for H dissolved in α-UH3(0, 1/4, 1/2), β- UH3(0, 1/4, 1/2), β- UH3(1/4, 1/4, 1/4) and UO2(0, 0, 1/2) interstitials as a function of doping concentration

在間隙插入H原子后，UO2晶格中的八面體間隙(0, 0, 1/2)摻雜氫原子后能量顯著升高，這與UO2中氫溶解度極低的實驗結論相符. 兩種氫化物晶格的氫溶解能及其升高的幅度均較小，其大小關系為β-UH3(0, 1/4, 1/2) >α-UH3(0, 1/4, 1/2) >β-UH3(1/4, 1/4, 1/4)，這說明較大的間隙摻入氫原子后發生的畸變較小，因而氫溶解能及其隨摻雜濃度的升高幅度較小. 比其他兩種間隙小一個量級. 在摻雜濃度較小時，體系的溶解能近似呈線性上升，表明距離較遠的間隙可近似視為孤立，這些位置上摻雜基本互不影響. 更高的摻雜濃度溶解能的變化偏離線性，且往往是正偏離，表明摻雜H原子之間的相互作用使得體系的能量上升.

β-UH3單胞中(1/4, 1/4, 1/4)間隙位摻雜一個氫原子的的溶解能僅為0.008 eV，而α-UH3(0, 1/4, 1/2)間隙摻雜一個氫原子的溶解能為0.069 eV，為兩種晶格中溶解氫原子的優先位點，因此下文主要就這兩種間隙位的氫原子擴散擴散討論.

3.4 氫在幾種介質中的擴散勢壘

根據擴散Arrhenius方程

(4)

不考慮指前因子差異的情況下，具有更低遷移勢壘的晶格中氫的擴散速率更高，因此擴散勢壘可以在一定程度上體現氫在材料中擴散速率的快慢. 為對比氫原子在氫化反應過程中可能涉及的介質中的擴散特性，下面計算H原子在α-UH3(0, 1/4, 1/2)間隙、β-UH3(1/4, 1/4, 1/4)間隙、UO2(0, 0, 1/2)間隙及PdHx(0, 0, 1/2)間隙中擴散的最小能量路徑，及對應的擴散勢壘.

3.4.1α-UH3(0,1/4,1/2)間隙

由于氫原子半徑較小，它在晶格中的擴散往往通過格點原子的間隙進行. 但完整無缺陷的晶格中氫原子的擴散較難，因為它會導致晶格原子發生較大畸變，使得擴散過程的勢壘較高. 圖4是α-UH3中氫原子沿(0, 1/4, 1/2)間隙直接擴散的最小能量路徑，可以看出其擴散勢壘高達1.04 eV，表明氫原子采取這種方式進行擴散的概率較小.

圖4 間隙H原子在α-UH3直接擴散的MEP曲線Fig. 4 The minimum energy path for direct diffusion of H atoms between α-UH3 interstitials

考慮到α-UH3中存在大量格點氫原子，且U原子對周圍的H原子接近于金屬氫中的弱陷獲作用，格點處的氫原子較容易脫離平衡位置發生遷移. 因此，可以假設處于間隙的氫原子與格點上氫原子之間發生協同擴散，即位于間隙處的氫原子向擴散路徑上的格點位移動，而原先位于格點處的氫原子同時向下一個平衡間隙位置移動. 在這種擴散模式下，除了擴散原子與協同擴散的原子外，其他原子發生的原子位移很小，因而擴散勢壘與直接擴散相比有顯著的降低.α-UH3中H通過協同擴散進行遷移的反應路徑如圖5所示. 可以看到，最小能量路徑呈現出周期性起伏，勢壘僅為0.16 eV.

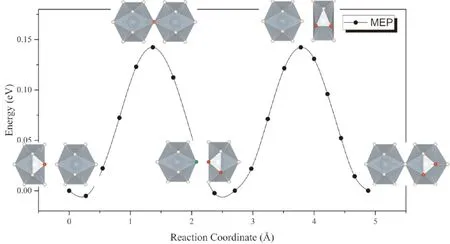
圖5 H原子在α-UH3中通過格點原子H協同擴散的MEP曲線Fig. 5 The MEP of interstitial H diffusion in α-UH3 lattice with the cooperation of H in lattice position

3.4.2β-UH3(1/4,1/4,1/4)間隙

同樣考慮上述兩種擴散模式，一種是位于間隙的氫原子直接向相鄰同種間隙擴散，可以看到擴散過程種附近的UH12正二十面體發生較大畸變，因而勢壘同樣高達0.93 eV (圖6)，表明按照此種方式進行擴散的速率非常低，這一點與通過α-UH3間隙擴散的情形相似. 而考慮間隙處的氫原子與UH12正二十面體中的一個氫原子協同擴散的話，擴散勢壘大幅降低到了0.09 eV (圖7).

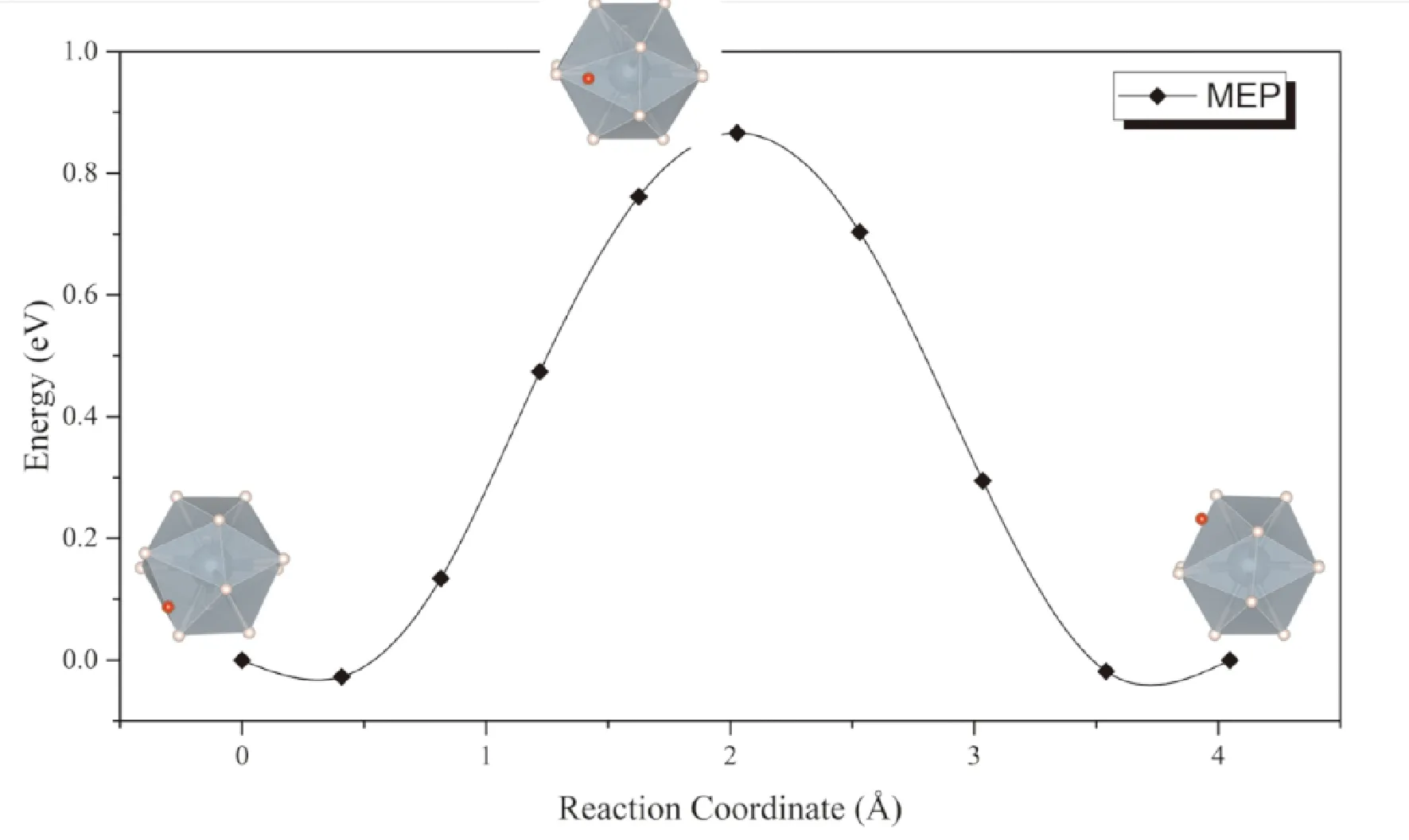
圖6 H原子通過β-UH3間隙擴散的MEP曲線Fig. 6 The MEP for direct diffusion of interstitial H in β-UH3

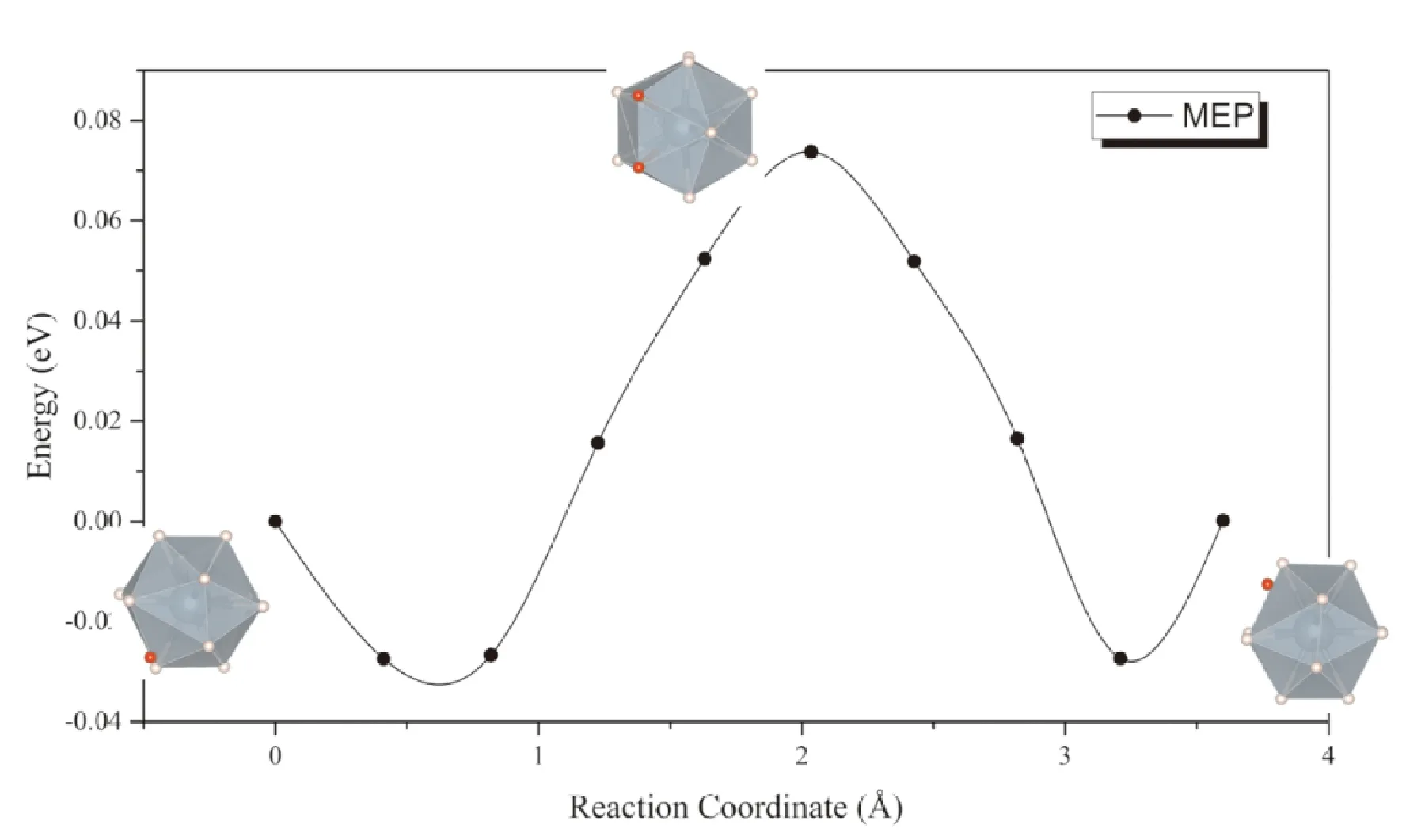
圖7 H原子在β-UH3中通過格點原子協同擴散的MEP曲線Fig. 7 The MEP of interstitial H diffusion in β-UH3 lattice with the cooperation of H in lattice position

由于氫原子的溶解能較低，在與α-UH3密度相近的情況下，β-UH3中氫的溶解度比α-UH3要高. 而從圖7可以看出，同樣是在二十面體上的格點氫原子協同下，氫在β-UH3中擴散的勢壘也顯著低于其在α-UH3中擴散的勢壘. 因此，氫通過β-UH3進行擴散的速率，將顯著高于其通過α-UH3擴散的速率.

3.4.3UO2(0,0,1/2)間隙

對擴散勢壘的計算主要考慮H原子在相鄰八面體間隙之間擴散的情形. 從圖8中可以看出，擴散過程中能量鞍點的構型為氫原子位于兩個O原子中間，三者在一條直線上的情形. 計算結果表明H原子在UO2晶格中的擴散勢壘的計算值為213 kJ·mol-1(2.20 eV)，顯著高于57-60 kJ·mol-1的實驗值. 這表明H原子通過鈾氧化物的擴散主要通過間隙、晶界等氧化層內的缺陷進行擴散，而在完整晶格中的擴散幾乎可以忽略.

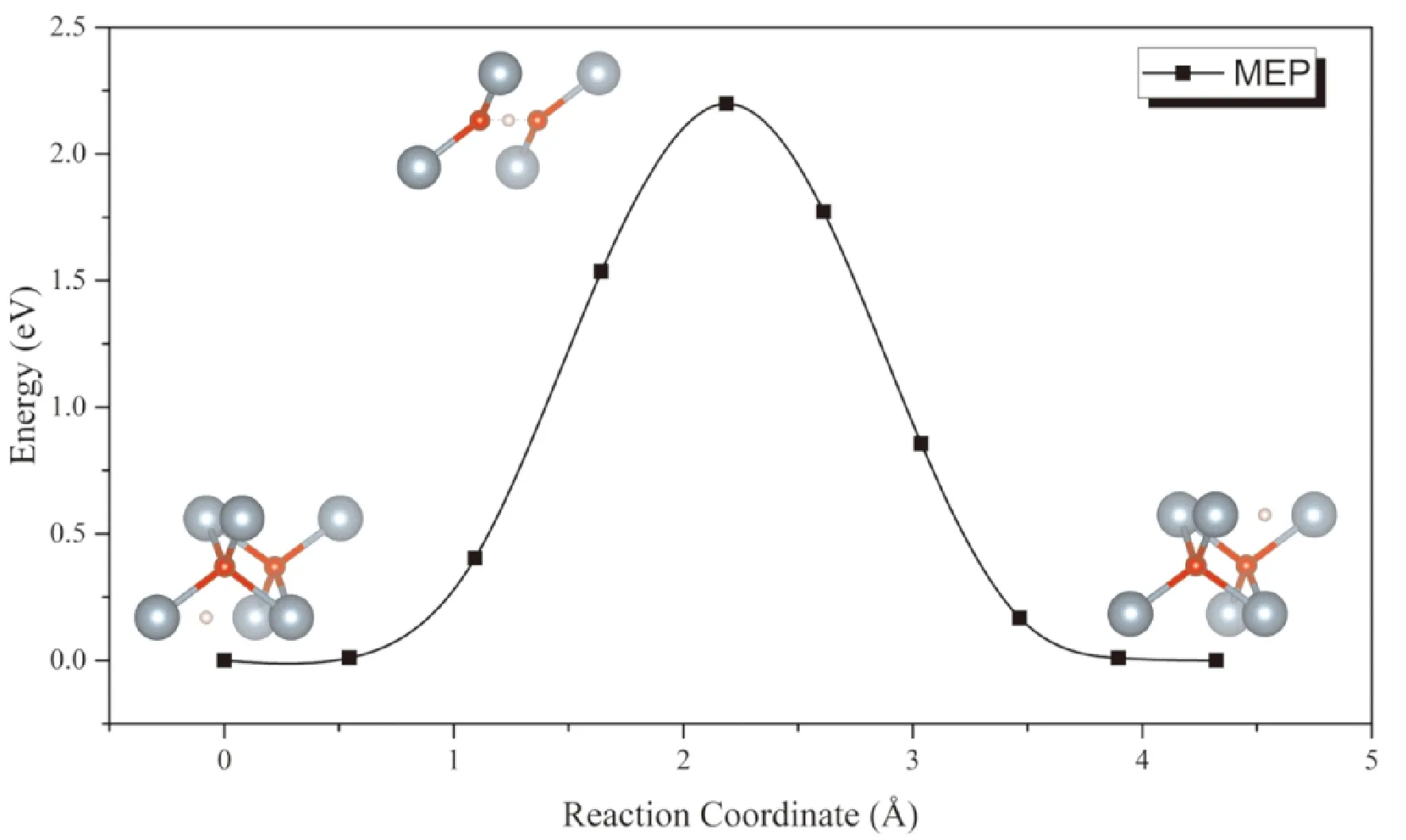
圖8 H原子在UO2間隙通過擴散的MEP曲線Fig. 8 The MEP of H diffusion in UO2 interstitials

3.4.4PdH0.5(0,0,1/2)間隙

依據文獻報道[35]，PdHx晶格中H占據Pd晶格的八面體間隙，形成NaCl型晶體結構. PdHx晶格中氫原子含量升高，Pd的面心立方骨架結構不變，氫原子隨機填充剩余八面體間隙，導致其晶格發生一定膨脹. 為了簡化討論，選取PdH0.75的本征原子配比，其中H原子分別占據Pd晶格的三個八面體間隙位，考慮其中一個摻雜H原子向鄰近間隙移動的擴散模型.

由于PdH0.5晶格中僅有一半的八面體間隙被H原子隨機占據，H原子可以在相鄰的間隙之間迅速遷移. 從圖9中可以看出，擴散過程中能量鞍點的構型為氫原子位于Pd組成的八面體籠的一條棱的中點(即相鄰的四面體間隙位)，此時體系能量較低，但在這種過渡態構型下Pd原子骨架仍發生了一定的變形，這導致H原子在PdH0.5晶格中擴散的勢壘為0.19 eV，略高于H原子在α-UH3中的擴散勢壘.

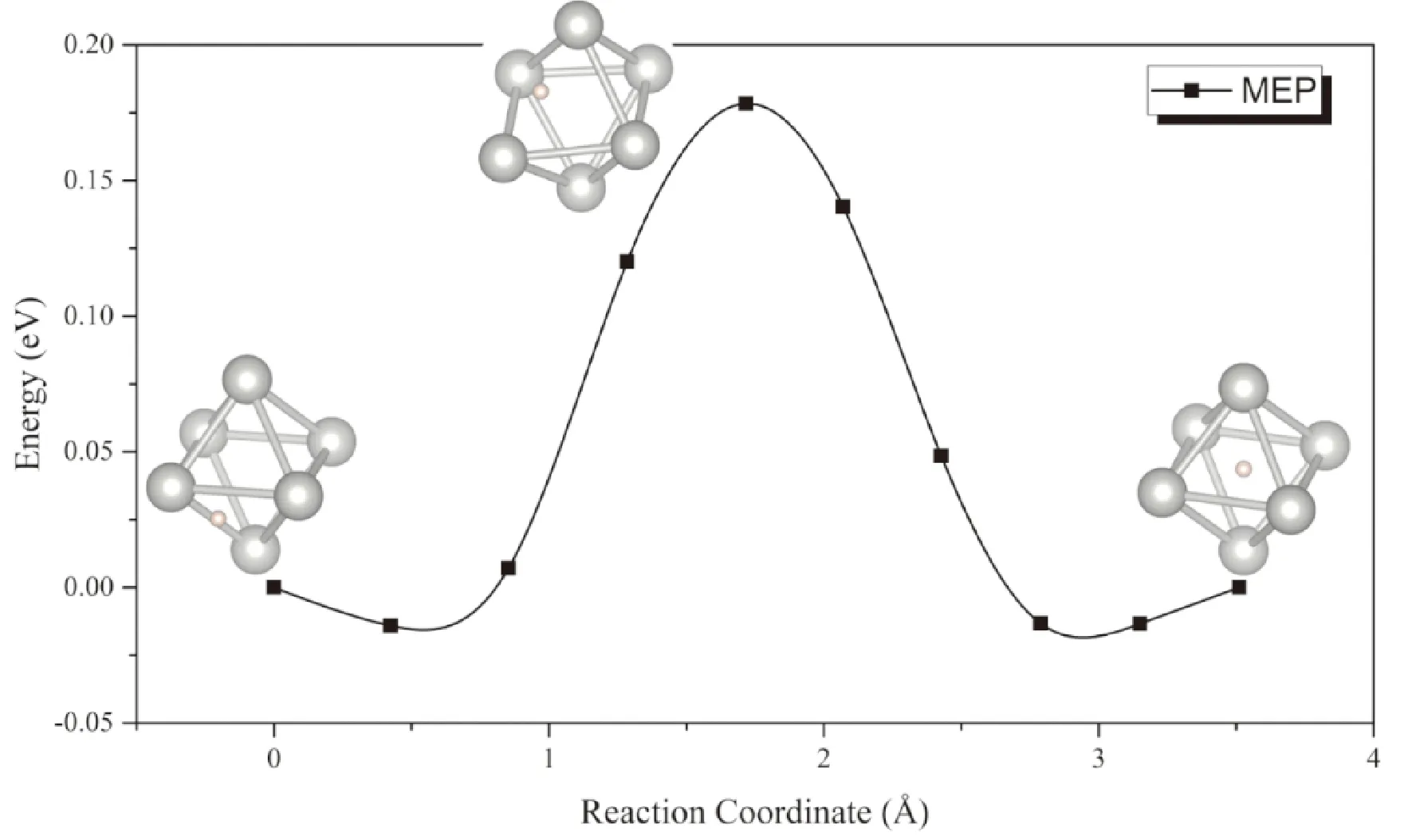
圖9 PdH0.75中氫原子在Pd晶格八面體間隙移動的MEP曲線Fig. 9 The MEP of the migration of H atom between octahedral interstitials in PdH0.75

3.5 幾種介質中氫擴散勢壘的討論

α-UH3、β-UH3、UO2、PdHx四種介質中H的摻雜溶解能和擴散勢壘如表2所示.

表2 四種介質中氫摻雜的溶解能和擴散勢壘

Table 2 Energy of dissolution and diffusion barriers of H atoms in four mediums

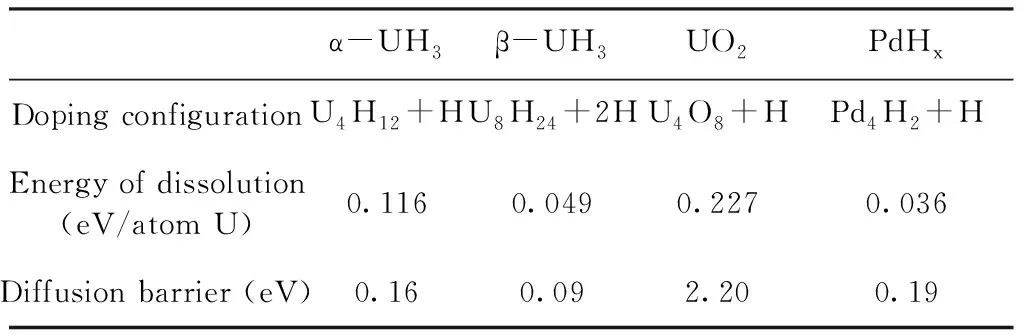
α-UH3β-UH3UO2PdHxDoping configurationU4H12+HU8H24+2HU4O8+HPd4H2+HEnergy of dissolution(eV/atom U)0.1160.0490.2270.036Diffusion barrier (eV)0.160.092.200.19

由上面的分析可以看出，無論是α-UH3還是β-UH3中，氫原子單獨在間隙中進行擴散的勢壘非常大，接近1 eV；而通過格點處氫原子協同進行擴散，其勢壘則非常小，分別為0.16 eV (15.5 kJ·mol-1)和0.09 eV (8.7 kJ·mol-1)，甚至可以借助熱運動進行擴散. 同時由于鈾氫反應為放熱反應，因此氫的擴散不會成為反應的速率控制步驟. 而氫在α-UH3晶格中引發的溶解能比β-UH3中大，且擴散勢壘也相對較高，因此氫在α-UH3晶格中的擴散速率相對較低.

考慮到氫在氫化物表面可以自發解離，可以預計，一旦氫氣與鈾氫化物直接接觸，尤其是與溶解度和擴散速率均較高的β-UH3直接接觸，將很快解離成氫原子并擴散通過氫化物層到達反應界面，加上β-UH3具有超高的比表面積[36, 37]，這也是氫化物具有自催化效應的原因. 向鈾表面沉積一層金屬Pd膜，一方面可以通過限制到達反應界面的氫通量來降低反應速率，使產物中α-UH3的比例升高，另一方面可以限制β-UH3與氫的接觸，從而抑制β-UH3的生成.

4 結 論

第一性原理計算結果表明，固溶氫原子在α-UH3和β-UH3中能量最低的間隙位分別為(0, 1/2, 1/4)和(1/4, 1/4, 1/4)，且低濃度下氫原子溶解能隨摻雜濃度近似線性增加. 氫在UO2中具有非常大的擴散勢壘(2.2 eV)，表明完整UO2晶格中氫的擴散非常困難，使得氫的擴散需通過空位等缺陷進行. 在α-UH3和β-UH3中，間隙氫原子可通過格點氫原子進行協同擴散，使得它們具有非常低的擴散勢壘，但α-UH3中擴散勢壘(0.16 eV)高于β-UH3中的擴散勢壘(0.09 eV)，對應著較低的氫化反應速率. Pd層中氫的擴散勢壘為0.19 eV明顯高于β-UH3而與α-UH3相近，表明Pd膜覆蓋的情況下，其反應速率與表面生成α-UH3的情形相近，這可以部分解釋Pd膜覆蓋下鈾氫化反應主要產物為α-UH3的現象.