圖的符號星獨立數

汪曉馬，葉淼林

(安慶師范大學數學與計算科學學院，安徽安慶246133)

隨著圖論的快速發展，涌現出許多重要的結論和分支。最近，Nikiforov給出了譜半徑和哈密爾頓圖的最小度[1]；Zhou給出了k-連通圖的一些充分條件與哈密爾頓連通圖譜的一些充分條件[2-3]。另外，圖的控制理論是圖論的一個重要而有趣的分支，圖的控制理論也由原始的點控制逐步向邊控制發展，徐保根在文獻[4-5]中給出的“圖的符號星控制”概念就是其中一個重要的邊控制，本文中“圖的符號星獨立數”概念源于“圖的符號星控制數”。

設G=(V,E)是階數為n的簡單圖，圖G的頂點集記為V(G)={v1,v2,…,vn},圖G的邊集記為E(G)={e1,e2,…,en},用e(G)表示圖G的邊的個數，即e(G)= ||E(G)，G的頂點v的度d()v是指G中與v關聯的邊的數目，用Δ=Δ(G)和δ=δ(G)分別表示圖G的最大度與最小度。圖G與H的并表示為G?H，即G?H=(V(G?H),E(G?H))。對于實數x，用■■x表示不大于x的最大整數，■■x表示不小于x的最小整數。本文中未說明的符號及術語與參考文獻[6-7]一致。

下面先給出一些相關定義、引理及證明。

定義1設G=(V,E)是一個圖，如果存在一個雙值函數f:E(G)→{-1,1}對任意v∈V(G)，都有，則稱f是圖G的符號星獨立函數。

定義2稱W(G)=f為圖G的符號星獨立函數 }為圖G的符號星獨立數，并稱此時的符號星獨立函數為G的一個最大符號星獨立函數。

其中，邊集{e ∈E(G)|f是圖G的符號星獨立函數且f(e)=1}叫做圖G的符號星獨立集；邊集{e∈E(G)|f是圖G的最大符號星獨立函數且f(e)=1}叫做圖G的最大符號星獨立集。

顯然，任何非空圖的符號星獨立函數總是存在的，在每條邊上都取值為-1即可。對于任何有限圖G，最大符號星獨立函數總是存在的，但不一定唯-一。

規定：空圖的符號星獨立數為0，即W(Kn)=0。由定義可知，圖G的符號星獨立數也可以取正數、負數，例如，W(K2)=1,W(K3)=-1。

引理1設v是圖G的一個頂點，f是G的一個符號星獨立函數，則有

證明由圖G的符號星獨立函數定義直接可得。

引理2(K?nig,Egerváry)[8]設圖G是一個二部圖，則G的最大邊獨立數等于最小點覆蓋數。

引理3圖G是一個二部圖，則G的最大邊獨立數至少為

證明設α′、β分別表示圖G的最大邊獨立數與最小點覆蓋數。因為圖G的每個頂點至多覆蓋Δ(G)條邊，所以β個頂點至多覆蓋β?Δ(G)條邊，因此β?Δ(G)≥e(G)，即，由引理2，得

引理4[9]完全圖K2n是一個1-因子和n-1個哈密爾頓圈的和。

引理5[9]完全圖K2n是一個1-可因子化的。

下面給出本文的主要結論及證明。

定理1設G是任意n階圖，分別用no、ne表示圖G的奇度點個數和偶度點個數，則有

證明設f為圖G的最大符號星獨立函數，則

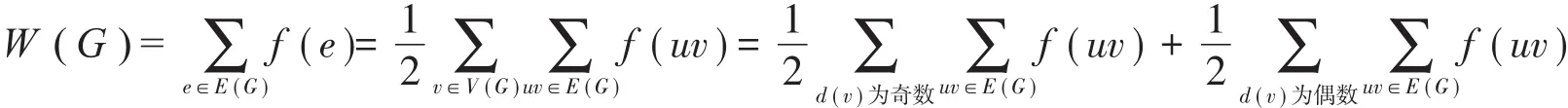
由引理1，得

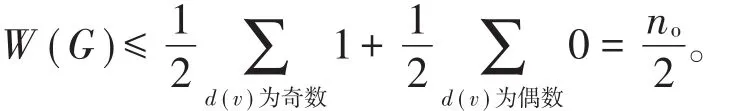
定理1給出了圖的符號星獨立數的上界。對于任何一個圖，偶數度頂點的個數不超過該圖頂點的個數。于是，從定理1的結論，容易得到下面的推論。

推論1設圖G是n階圖，則有

證明由定理1知，又因為no≤ n，故

事實上，推論1是定理1的一個平凡的推論，從這兩者的關系中，又可以得到如下的結論：

推論2設圖G是n階圖，則等式成立的充分必要條件是圖G中度數為偶數的點的個數為0且

證明（必要性） 設，由定理1知，于是n ≤ no，因此ne=0，即圖G中度數為偶數的點的個數為0，并且W(G)=

下面分析圖的符號星獨立函數的概念與圖的匹配集概念之間的關系。事實上，只要讓圖的匹配集中邊賦值為1而其他邊賦值為-1，就得到了該圖的一個符號星獨立函數，由此可以得到圖的符號星獨立數的一個下界。

定理2對任意圖G，均有W(G)≥2α′-e(G)，其中α′為圖G最大匹配集中元素個數。

證明設M是圖G的一個最大匹配集，則有 ||M=α′。令

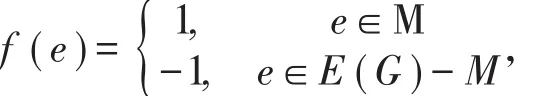
顯然f是圖G的一個符號星獨立函數(不一定是最大的符號星獨立函數)，故

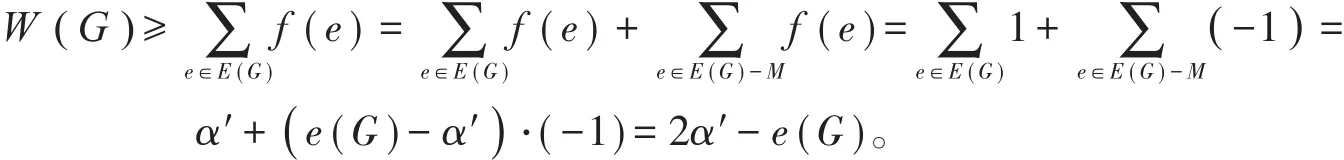
定理3設G是一個二部圖，則

證明由定理2與引理3可得W(G)≥2α′-e(G)≥

推論3設G是一個二部圖，若Δ(G)≤2，則W(G)≥0。

定理4設Cn是階為n的圈，則當n為奇數時，W(Cn)=-1；當n為偶數時，W(Cn)=0。

證明當n為偶數時，給圈Cn每條邊交錯的取值-1和1，不難驗證，這樣的賦值正好得到Cn的一個最大符號星獨立函數，并且-1與1的個數正好相等，所以W(Cn)=0。當n為奇數時，用同樣的方法給圈Cn每條邊賦值，必然恰有兩條相鄰的邊都賦值-1，容易證明，這樣的賦值也正好得到Cn的一個最大符號星獨立函數，并且-1的個數比1的個數恰好多一個，因此W(Cn)=-1。

定理5設圖G為歐拉圖，則有

（1）當 ||E(G)為奇數時，W(Cn)=-1；

（2）當 ||E(G)為偶數時，W(Cn)=0。

證明由歐拉圖的定義以及用定理4的方法在歐拉閉跡的每條邊上賦值，即可得證。

在圖的控制理論中，求解圖的符號星控制數是比較困難的。類似地，求解一個圖的符號星獨立數也是困難的。最后給出完全圖Kn的符號星獨立數。

定理6設Kn是n(n≥2)階完全圖，則

證明(證法一)（1）當n為奇數時，Kn的每個頂點的度數n-1為偶數，從而Kn是歐拉圖。下面分兩種情況討論。

(i)當n-1為4的倍數時，設n=4k+1（k為正整數），則為偶數，由定理5（2）知，W(G)=0。

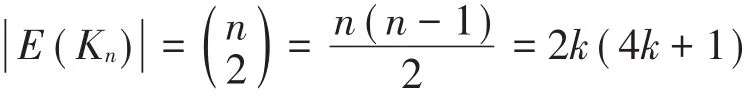
(ii)當n-1不是4的倍數時，設n=4k-1（k為正整數），則

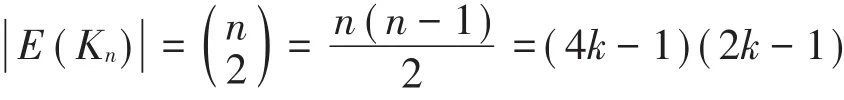
為奇數，由定理5（1）知，W(G)=-1。

（2）當n為偶數時，當n=2時，定理顯然成立。下設n≥4。

ni爾頓圈Hi的長度n是偶數。

定義Kn的一個符號星獨立函數f：當e∈F時，令f(e)=1;在每個哈密爾頓圈Hi上，交錯地取f的值為1和-1，因為Hi的長度n是偶數，所以在每個哈密爾頓圈Hi上1與-1的個數相等。顯然，這樣的定義滿足符號星獨立函數的定義。因此

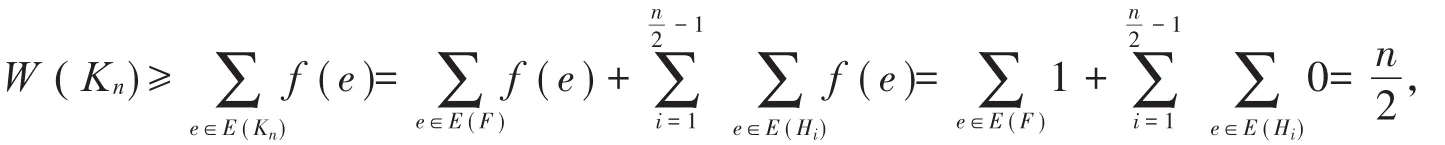
(證法二)（1）同證法一。

（2）當n為偶數時，當n=2時，定理顯然成立。下設n≥4。由引理5可知Kn是1-可因子化的，所以可設圖Kn分解成n-1個是1-因子Fi(i=1,2,…,n-1)之和。令

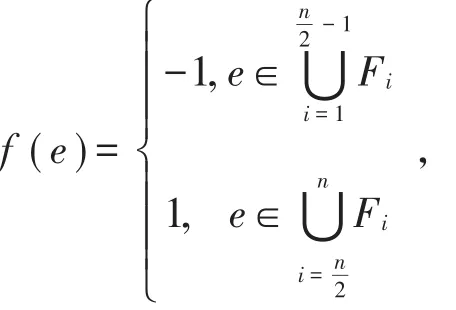
顯然，f是圖Kn的一個符號星獨立函數，所以，再由推論1的結論得W(Kn)=。

實際上，從定理6中偶數階完全圖的符號星獨立數的結論可知，定理1中n階圖符號星獨立數的上界其實是上確界。