環R+uR+vR+uvR上的斜常循環碼

劉 瑋，宋賢梅

(安徽師范大學數學與統計學院，安徽蕪湖241003)

眾所周知，循環碼是編碼中的一種重要碼，它能夠高效快速完成譯碼過程，從而在實踐中得到廣泛的運用。1994年，Hammons等證明了某些二元非線性碼可以看作是Z4上的循環碼Gray像[1]。自此之后，有限鏈環及一些特殊的有限鏈環上的循環碼及其相關的研究受到越來越多的關注。萬哲先等系統介紹了Galois環上的循環碼[2]；Wolfman等研究了Z4上的負循環碼與循環碼[3]；Dinh研究了Galois環上長為偶數的負循環碼[4]；錢建發研究F2+uF2上(1+u)-常循環碼和循環碼[5]；朱士信等研究了Fp+uFp上的常循環碼和Gray像[6]；Boucher等首次提出了Fp上的斜循環碼概念[7]，并說明斜循環碼的漢明距離大于已知最好的線性碼，其后又研究了Galois環上的斜常循環碼[8]；Jitman等研究了有限鏈環上的斜常循環碼及對偶碼[9]；宋賢梅等研究了非有限鏈Fq+vFq+v2Fq上的斜常循環碼及對偶碼的相關性質[10]。隨著環的不斷推陳出新，環之間存在著一定的局限性和關聯性，從最開始普通的循環碼逐步研究到更深層次的斜循環碼，到目前的斜常循環碼并取得豐富的結論。因不同環上的斜常循環碼具有相似的結論，所以本文構造全新的環來研究上述文獻中的結論和性質。針對環?=R+uR+vR+uvR(u2=-u,v2=-v,uv=vu)上的斜常循環碼及對偶碼性質，得到線性碼C是斜常循環碼的充要條件，并討論斜常循環碼C的生成多項式與對偶碼C⊥的生成多項式。

1 預備知識

記環?=R+uR+vR+uvR，其中u,v滿足u2=-u,v2=-v,uv=vu,R為有限鏈環。 r表示有限鏈環R的極大理想且rl=0,l為其冪零指數，則R r是域，記為K。記 ||K =q，則 ||R =ql。令e1=1+u+v+uv,e2=uv,e3=-u-uv,e4=-v-uv，令ei=∈ R,i=1,2,3,4，且當i≠ j,eiej=0,e1+e2+e3+e4=1，因此有直和分解

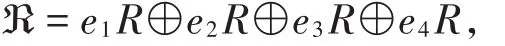
且?中元素r可唯一表示為

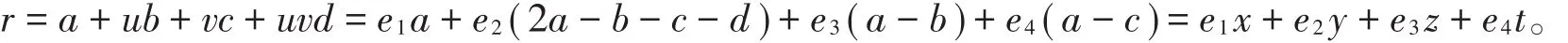
易知1+2u是環?的一個單位，且滿足(1+2u)e1=e1,(1+2u)e2,(1+2u)e3=-e3,(1+2u)=e4，?n={(a0,a1,…,an-1)|ai∈?,i=0,1,…,n-1 }是一個交換環。若C是?n的非空子集合，則稱C是?上長為n的碼。若C是?n的R-子模，稱C是R上長為n的線性碼。

設X=(x1,x2,…,xn),Y=(y1,y2,…,yn)∈?n，定義X,Y的歐幾里得內積為

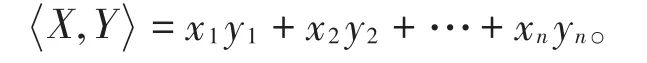
設C是長為n的碼，C⊥={ }x∈?n|x,c=0,?c∈C 稱為C的歐幾里得對偶碼。

設θ是有限鏈環R的一個自同構，定義?上的自同構θˉ滿足：

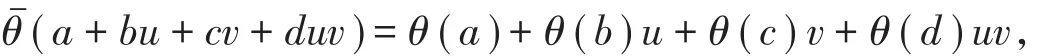
?到R4的Gray映射?定義為對任意r=a+ub+vc+duv∈?有

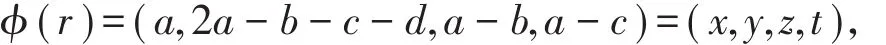
擴展到?n上，則對任意r=a+ub+vc+duv∈?，其中ci=e1xi+e2yi+e3zi+e4ti(i=0,1,2,…,n-1)有

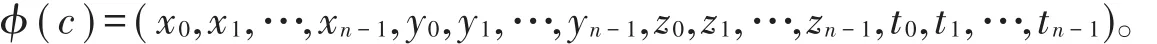
設C是?長為n的線性碼，對c∈C，c的Gray重量為WG(c)=WH(x,y,z,t)，易知?是?n到?4n的雙射且是一個保距映射。

下面給出碼的直和與卡氏積定義，設B1、B2、B3、B4是?上長為n的線性碼，

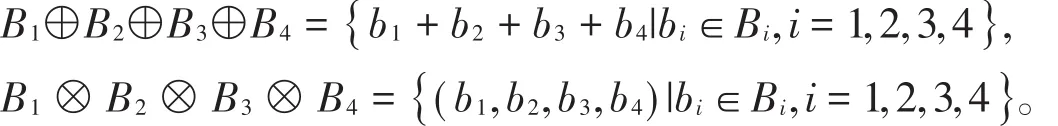
假設C為環?上長為n的線性碼，定義集合：

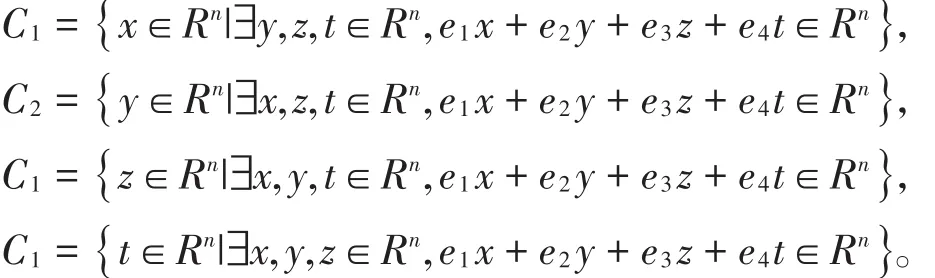
易知：

(1)Ci(i=1,2,3,4)是R上長為n的線性碼；

(2)線性碼C可以唯一表示為e1x⊕e2y⊕e3z⊕e4t；

(3)C= |C1|?| C2|?|C3|?|C4|。

通過線性碼C的直和分解可以得到C的對偶碼C⊥及?(C⊥)與?(C)⊥的相關性質，從而得到如下命題。

命題1設C=e1C1⊕e2C2⊕e3C3⊕e4C4是?上長為n的線性碼，則下面結論成立：

（1）C⊥=e1C1⊥⊕e2⊕e3⊕e4，

（2）?(C)=C1?C2?C3?C4且 | ?(C)|= |C1|?| C2|?|C3|?| C4|，

（3）?(C⊥)=C1⊥? C2⊥? C3⊥? C4⊥。

證明(1)定義集合={x∈ Rn|?y,z,t∈ Rn,e1x+e2y+e3z+e4t∈ C⊥}，同理定義,易知 C⊥=e1⊕e2⊕e3⊕e4。下面僅需證明=(i=1,2,3,4)，不妨證=，對任意x ∈，有e1x+e2y+e3z+e4t=c′∈ C⊥，因此對任意x′∈ C1,有e1x′+e2y′+e3z′+e4t′=c∈ C且＜ c,c′＞=e1xx′=0，從而xx′=0，則?。另一方面，若x∈，則c′=e1x′+e2y′+e3z′+e4t′∈ C⊥，有＜ e1x,c′＞=e1xx′=0，于是x∈ ?⊥1，故=。同理可證=,=,=,所以 C⊥=e1+e2+e3+e4。

(2)由線性碼C的直和表示及?的定義，易知?(C)?C1?C2?C3?C4。對任意c=(x,y,z,t)∈C1?C2?C3?C4，令 r=e1x+e2y+e3z+e4t，則 r∈C 且 ?(r)=c=(x,y,z,t)，故C1?C2?C3?C4??(C)。因此?(C)=C1?C2?C3?C4，注意到?是雙射，所以

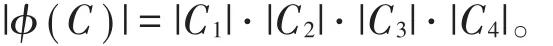
(3)由(1)(2)以及?的定義易知?(C⊥)??(C)⊥且注意到?是雙射，于是

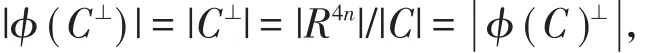
所以? (C⊥)= ? (C)⊥，類似(1)的證明有? (C)⊥=???。

2 環?上的斜常循環碼

定義1設是?上的自同構，λ是?的單位，ρθˉ,λ是?n的自同態，若對任意c=(c0,c1,…,cn-1)∈ C有ρθˉ,λ(r0,r1,…,rn-1)=(ˉ(λ)ˉ(rn-1),ˉ(r0),…,ˉ(rn-2))∈ C，則稱碼C是斜常循環碼或- λ-常循環碼。 特別地，當λ=1時，稱C為斜循環碼；當λ=-1時，稱C為斜負循環碼。

引理1設n為正整數是?的一個自同構，xn-(1+2u)∈?[x;，則下列說法等價：

（1）〈xn-(1+2u)〉是? [x;的雙邊理想；

（3）xn-(1+2u)是? [x;的中心。

證明(3)?(1)顯然。

(1)?(2)對任意的 ax∈?，由條件(1)知 ax(xn-(1+2u))=(xn-(1+2u))ax，即 a(1)xn+1-1+2u)x=(a)xn+1-(1+2u)ax，比較系數得(a)=a，即|＜＞ ||n且(1+2u)=1+2u。

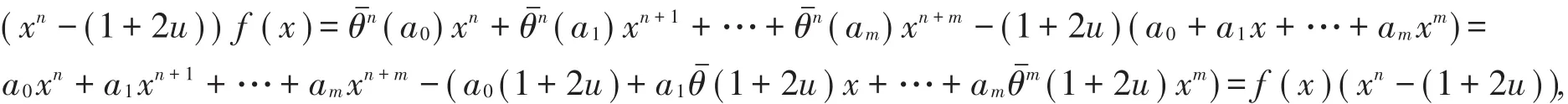
所以xn-(1+2u)是? [x;的中心。

注下面討論的內容，均是在〈xn-(1+2u)〉是雙邊理想的前提下，因此需要條件θˉ的階整除n,θ(1+2u)=1+2u。

定理1設C=e1C1⊕e2C2⊕e3C3⊕e4C4是?上長為n的線性碼，則C是θˉ-(1+2u)-常循環碼當且僅當C1、C4是?上長為n的斜循環碼，C2、C3是?上長為n的斜負循環碼。

證明設r=(r0,r1,…,rn-1)∈C，其中ri={e1ai+e2bi+e3di+e4di∣ai,bi,ci,di∈R(i=0,1,2,…,n-1)}，令a=(a0,a1,…,an-1),b=(b0,b1,…,bn-1),c=(c0,c2,…,cn-1),d=(d0,d1,…,dn-1)，可知

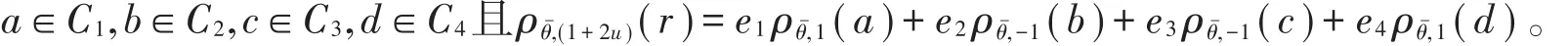
因此 ρθˉ,(1+2u)(r)∈ C 的充分必要條件是 ρθˉ,1(a)∈ C1,ρθˉ,-1(b)∈ C2,ρθˉ,-1(c)∈ C3,ρθˉ,1(d)∈C4，即 C 是 ? 上長為n的斜常循環碼的充分必要條件是C1、C4是?上長為n的斜循環碼，C2、C3是?上長為n的斜負循環碼。

命題2設C=e1C1⊕e2C2⊕e3C3⊕e4C4是?上長為n的(1+2u)-線性碼，gi(x)是Ci的生成多項式，且i=1,4時，gi(x)右整除xn-1；當i=2,3時，gi(x)右整除xn+1，則存在唯一的g(x)=e1g1(x)+e2g2(x)+e3g3(x)+e4g4(x)∈ ? [x;，使得C=＜ g(x)＞，g(x)右整除xn-(1+2u)且|C|=

證明令g(x ) =e1g1( x ) +e2g2( x ) +e3g3( x ) +e4g4( x )，下證C=＜g(x)＞。 一方面，易知C?〈e1g1(x),e2g2(x),e3g3(x),e4g4(x)〉，而eigi( x ) =eig( x )(i =1,2,3,4)，可得C?〈g(x)〉。另一方面注意到g(x)∈C，故C=〈g(x)〉。

現證g(x)右整除xn-(1+2u)。由條件可得存在fi(x)∈ ?[x;(i=1,2,3,4),使得

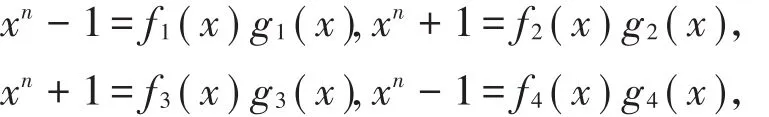
由于(1+2u)e1=e1,(1+2u)e2=-e2,(1+2u)e3=-e3,(1+2u)e4=e4，于是

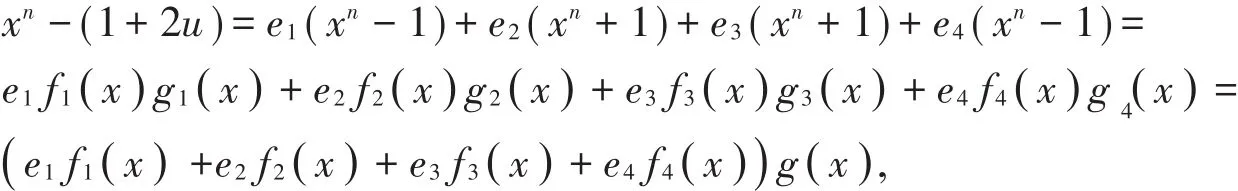
故g(x)是xn-(1+2u)的右因子。

最后，由于|C|=|C1|?|C2|?|C3|?|C4|,gi(x)是Ci的生成多項式，因此

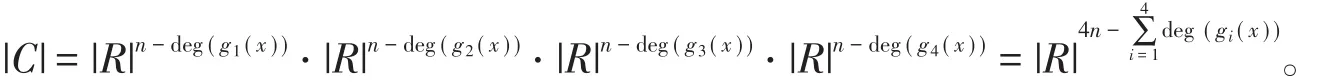
3 斜常循環碼的對偶碼

下面討論環?上長為n的斜常循環碼的對偶碼與其之間的聯系，并給出斜常循環碼的生成多項式。

定理2設θˉ的階是2且n為偶數，C是?上長為n的線性碼，則C是θˉ-(1+2u)-常循環碼當且僅當C⊥是θˉ-(1+2u)-1-常循環碼。

證明假設C是θˉ-(1+2u)-常循環碼，對任意u=(u0,u1,…,un-1)∈C有如下等式成立因此對任意v∈C⊥有0=〈(u),v〉，

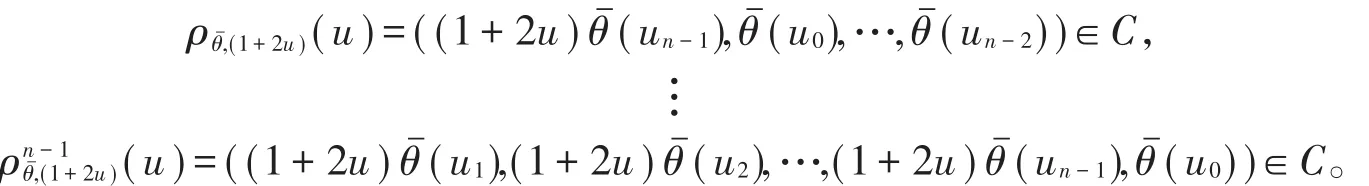
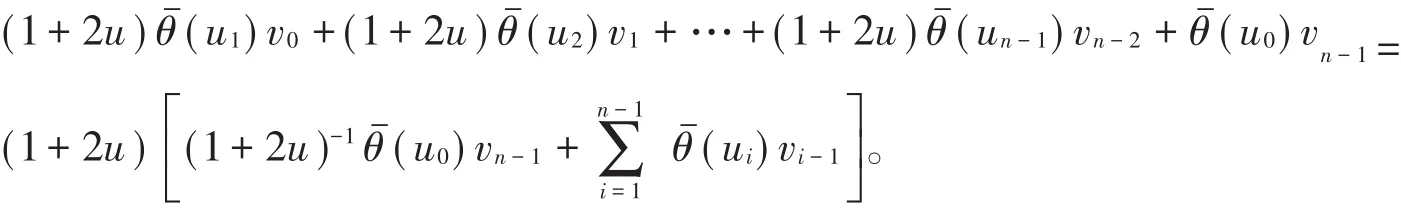
從而

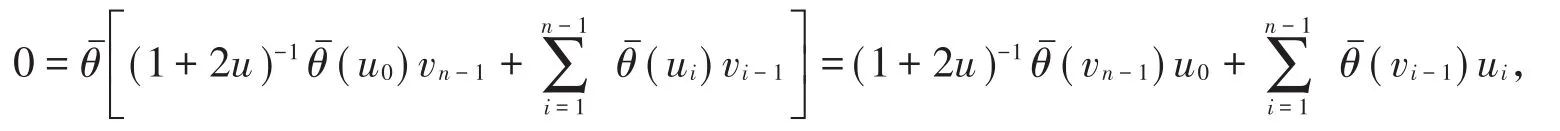
即〈(1+2u)-1θˉ(vn-1),θˉ(v0),…,θˉ(vn-2),(u0,u1,…,un-1)〉 =0，所以(1+2u)-1θˉ(vn-1),θˉ(v0),…,θˉ(vn-2))∈ C⊥，即 C⊥為θˉ-(1+2u)-1-常循環碼。

反之設C⊥為 θˉ-(1+2u)-1-常循環碼，利用前面類似的結論及(1+2u)-2=1 易知 C=(C⊥)⊥是θˉ-(1+2u)-常循環碼。

引理2設a(x)=a0+a1x+a2x2+ …+an-1xn-1,b(x)=b0+b1x+ …+bn-1xn-1∈?[x;θˉ]，則下面三條性質等價：

(1)當i∈{0,1,2,…,n-1}時，a(x)的系數向量與xi(xn-1φ(b(x)))的系數向量歐幾里得正交。

(2)(a1,a2,…,an-1)與(bn-1,θˉ(bn-2),…,θˉn-1(b0))以及它的θˉ-(1+2u)-常循環移位正交。

(3) 在? [x;θˉ]/(xn-(1+2u))中，a(x)b(x)=0。

定理3設|＜θˉ＞|=2，且n為偶數，C是?上長為n的θˉ-(1+2u)-常循環碼，g(x)是其首一的生成

(1)斜多項式xdeg(h(x))φ(h(x))是xn-(1+2u)的右因子。

(2)C⊥是由xdeg(h(x))φ (h(x))生成的θˉ-(1+2u)-1-常循環碼。

證明(1)由條件有|＜ θˉ＞ |∣n，且θˉ(-(1+2u))=-(1+2u)，于是

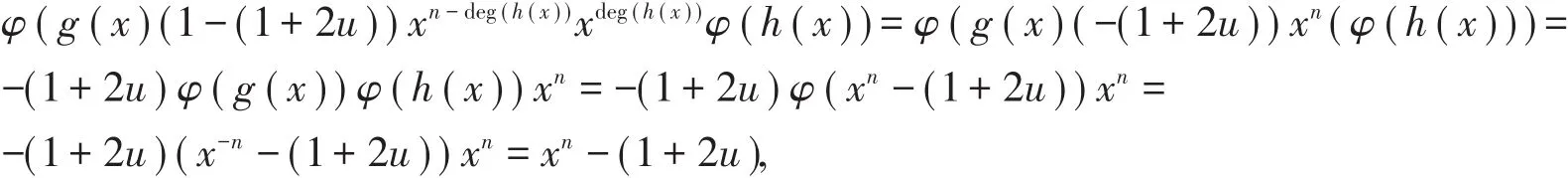
從而xdeg(h(x))φ (h(x))是xn-(1+2u)的右因子。

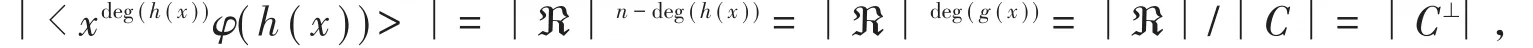
所以＜ xdeg(h(x))φ(h(x))〉=C⊥。