非線性三階常微分方程的多點邊值正解問題探索

何林海

?

非線性三階常微分方程的多點邊值正解問題探索

何林海

湘潭醫衛職業技術學院, 湖南 湘潭 411102

針對非線性三階常微分方程多點邊值正解問題研究較少的現狀，本文以錐上不動點定理為基礎，構建相應的等價方程，證明非線性三階常微分方程存在正解的可能性。計算結果表明：在Banach空間的錐中，當條件（）成立，若（1）成立，則至少存在3個正解；若條件（2）成立，則至少存在2個正解；若條件（3）、（4）成立，則存在至少1個正解。相對于已有文獻的研究結果，本文的解法有一定的創新價值。

三階常微分方程; 非線性; 多點邊值; 正解

三階常微分方程的多點邊值問題在天文學、流體力學等領域廣泛出現[1]。學者們對于該問題的正解研究進行了多方嘗試，試圖證明三階常微分方程存在1個或多個正解，并取得豐碩的成果。根據文獻[2]提出的三階常微分方程三點邊值問題，證明了至少存在3個正解[2]。文獻[3]同樣證明了三階常微分方程三點邊值至少存在3個正解[3]。文獻[4]則通過錐上不動點定理，證明三階常微分方程三點邊值存在正解的可能性[4]。但在以上文獻中，關于非線性三階常微分方程的多點邊值問題討論較少。本文基于錐上不動點定理，建立非線性三階常微分方程等價方程，通過計算證明非線性三階常微分方程有1個或多個正解，得到與當前文獻不同的結果，具備一定的創新價值。

1 非線性三階常微分方程的相關定義

定義1：設為Banach實空間，的錐為ì，稱之為非空閉凸集。該定義要滿足以下條件：∈，若∈，則≥0；，-∈，=0。

定義2：對于[0,1]，函數為凸泛函，滿足條件如下：(1+(1-)2)≥(1)+(1-)(2),,1,2∈[0,1]

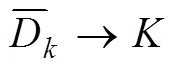
（1）若∥A∥≤∥∥，∈?D，則i(,D)=1；

（2）若有∈{0}，令1A+，∈?D，>0，則i(,D)=0；

2 計算結果與證明

首先對非線性三階常微分方程的邊值問題進行考慮，有：???()=()，∈[0,1] (1)

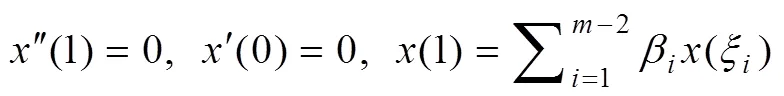
引理2：令0=0，-1=1，0=β-1=0，()∈[0,1]，式（1）（2）與下面等價：

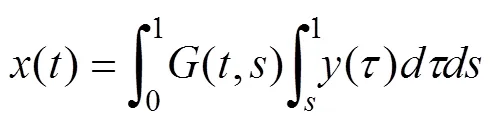
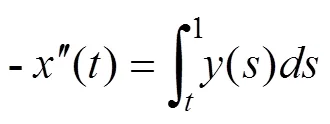
設(,)為邊值的問題，則下式成立：-??()=0 (6)

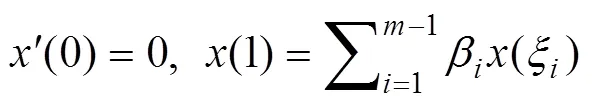
根據Green函數的定義與性質，對式（7）的邊值條件進行結合，得出下式：

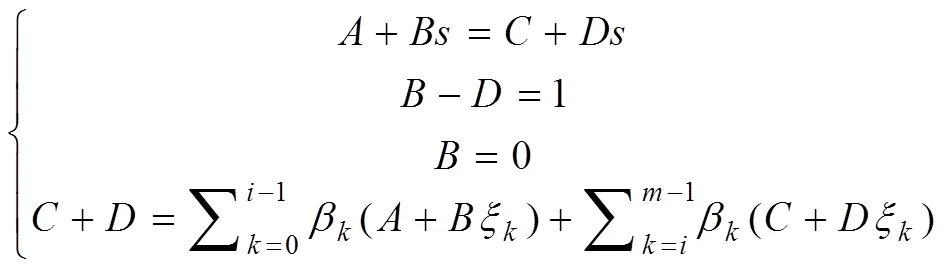
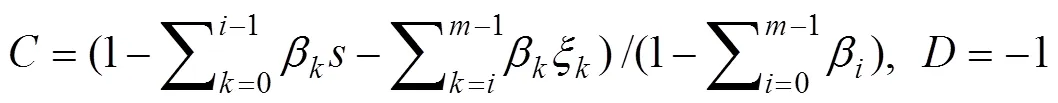
引理3：(,)滿足以下條件(,)≥0,,∈[0,1]。

對于-1≤≤，=1,2,…,-1,≥，下式成立：

綜合以上證明，(,)≥0,,∈[0,1]。

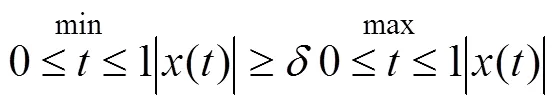
()具有凸性：((1)-(0))≤()-(0)。

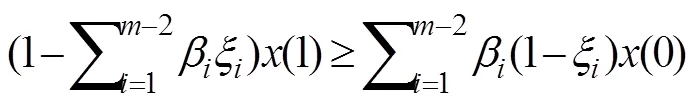
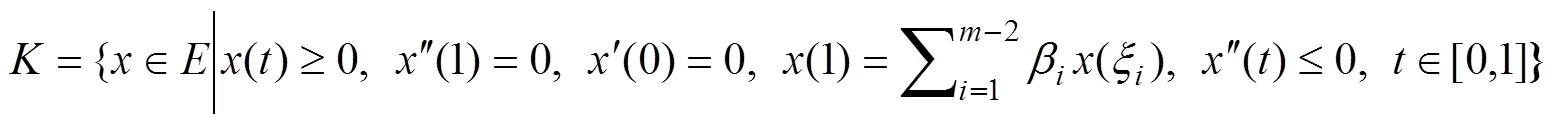
進一步計算：()=min{,1-},∈[0,1] (19)

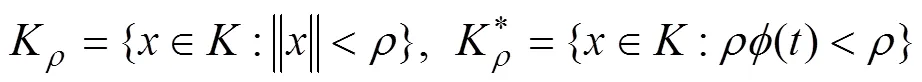
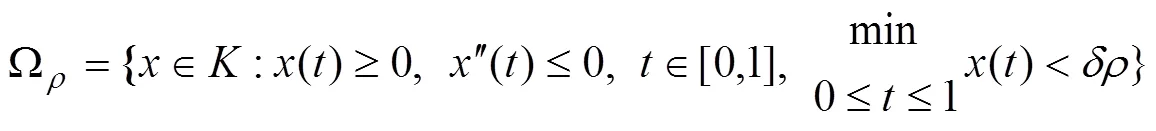
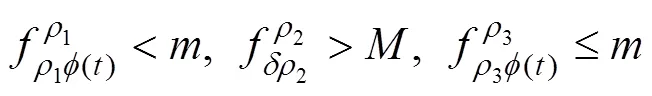
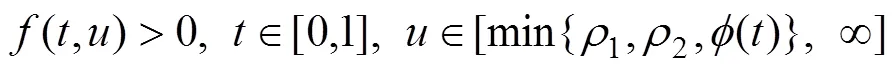
則非線性三階常微分方程的多點邊值問題在里面至少存在2個正解。

證明4：假設條件（1）成立，對輔助函數*(,)∈((0,1)×(0,∞),(0∞))進行計算：

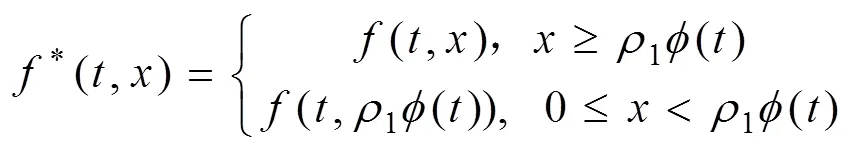
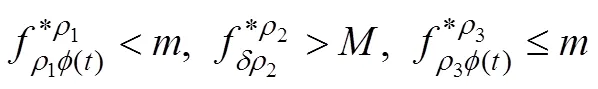
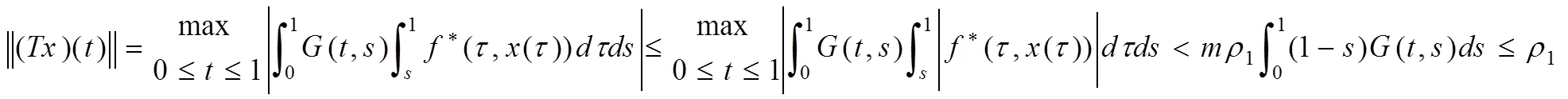
說明∥()∥≤∥∥，∈?。設()≡1，∈[0,1]，則∈1。以下必成立：1+，∈??2，≥0。否則必有：0∈??2，0≥0，得出0=0+0。但：

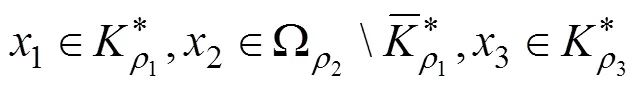
這樣就容易驗證（*）在[1(),∞]里面的正解，說明非線性三階常微分方程的多點邊值問題至少會存在3個正解。設條件（2）成立，存在的正解同樣可以證明，與定理1完全相似，因此得到以下結論：

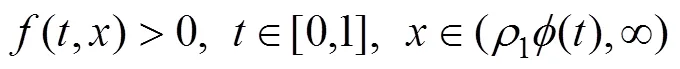
若條件（4）也成立，則（4）中有正常數1,2∈(0,∞)，并滿足以下條件：1<2，令：

則說明非線性三階常微分方程的多點邊值問題至少會存在1個正解。

3 討論

三階常微分方程組的類型對于解法有較大的影響，而且需要掌握相關的定理。最近幾年，關于非線性三階常微分方程的邊值正解問題，逐漸引起學者們的關注，但研究依然較少。Kreutz等通過萊格特·威廉姆斯定理，證明非線性三階常微分方程的兩點邊值問題，結果表明存在3個正解[5]。Mukhigulashvili研究了三階常微分方程的非線性特征值，在對該類型方程有界集的非線性特點考察的基礎上，構建問題正解的存在性以及多解性[6]。Bhaumik等探究了非線性三階常微分方程的正解，認為非線性項在有界集上的高度函數積分若恰當，則非線性三階常微分方程至少存在1~3個正解[7]。

4 結論

常微分方程是代數領域最簡單也最重要的方程組之一，三階常微分方程被人們廣泛用于解決日常問題，包括電子通信、化學反應、自動化、航空航天等領域的計算。本文在前人研究的基礎上，通過錐上不動點定理的運用，對非線性三階常微分方程的多點邊值正解問題進行了探索，主要得出以下結論：在Banach空間的錐中，當條件（）成立，若（1）成立，則至少存在3個正解；若條件（2）成立，則至少存在2個正解；若條件（3）、（4）成立，則存在至少1個正解。

[1] Yebdri M. On Weak Solutions of a Functional Differential Equation[J]. International Journal of Applied Mathematics & Statistics, 2018,57(2):83-88

[2] Bhaumik P, Ghosal S. Bayesian inference for higher-order ordinary differential equation models[J]. Journal of Multivariate Analysis, 2017,157(3):103-114

[3] Haug EJ. An Ordinary Differential Equation Formulation for Multibody Dynamics: Nonholonomic Constraints[J]. Journal of Computing and Information Science in Engineering, 2016,17(1):1-13

[4] Dallas S, Machairas K, Papadopoulos E. A Comparison of Ordinary Differential Equation Solvers for Dynamical Systems With Impacts[J]. Journal of Computational and Nonlinear Dynamics, 2017,12(6):37-48

[5] Hass H, Kreutz, C, Timmer J,. Fast integration-based prediction bands for ordinary differential equation models[J]. Bioinformatics, 2016,32(8):1204-1210

[6] Mukhigulashvili S. The mixed BVP for second order nonlinear ordinary differential equation at resonance[J]. Mathematische Nachrichten, 2017,290(2):393-400

[7] Bhaumik P, Ghosal S. Efficient Bayesian estimation and uncertainty quantification in ordinary differential equation models[J]. Bernoulli: official journal of the Bernoulli Society for Mathematical Statistics and Probability, 2017,23(4):3537-3570

Exploration for Multipoint Boundary Value Positive Solutions of Nonlinear Third Order Ordinary Differential Equations

HE Lin-hai

411102,

In view of the current situation that there are few studies on positive solutions of multi-point boundary value of third-order non-linear ordinary differential equations, this paper constructs corresponding equivalent equations on the basis of fixed point theorem on cone, and proves the possibility of existence of positive solutions of third-order non-linear ordinary differential equations. The results show that:in the coneof Banach space, if condition () holds and (1) holds, there are at least three positive solutions;If condition (2) holds, there are at least two positive solutions, and if condition (3) and (4) holds, there is at least one positive solution. Compared with the research results in the existing literature, the solution in this paper has some innovative value.

Third order ordinary differential equations; nonlinear; multipoint boundary values; positive solutions

O175.14

A

1000-2324(2019)02-0346-04

10.3969/j.issn.1000-2324.2019.02.036

2018-07-10

2018-09-20

何林海(1973-),男,本科,講師,研究方向:應用數學. E-mail:helinhai88@126.com