基于自動搜峰和shannon熵的車輛軸承多普勒畸變故障聲信號校正研究

(上海工程技術(shù)大學(xué) 城市軌道交通學(xué)院，上海 201620)

0 引言

滾動軸承是車輛(軌道車輛、汽車、電動車)必不可少的零部件，它承受著車輛牽引動力、制動阻力、齒輪嚙合不良引發(fā)的附加載荷。這些載荷使車輛出現(xiàn)軸承故障頻率較高，嚴(yán)重影響了車輛的運(yùn)行安全。所以對軸承故障診斷意義重大[1]。

在道旁安置傳聲器陣列來獲取運(yùn)動軸承發(fā)出聲音的故障診斷系統(tǒng)研究開始于1980年。在基于道旁聲學(xué)檢測的軸承故障診斷過程中，須使傳聲器安置位置與車輛之間有一段不可忽略的間隔，導(dǎo)致聲源在傳播過程中波長發(fā)生改變，傳聲器接收到的信號頻率與聲源發(fā)出的信號頻率不同，從而會造成信號存在多普勒畸變。這種多普勒畸變會使測量信號在頻域中產(chǎn)生頻帶展拓、頻率轉(zhuǎn)移等問題，使信號在頻域中較難分析出聲源所產(chǎn)生的故障特征頻率，降低了故障診斷的可靠性和準(zhǔn)確性[2]。為了解決多普勒畸變所帶來的問題，國內(nèi)外的許多學(xué)者對其進(jìn)行了深入的研究。國外的Stojanovic 等利用鎖相環(huán)技術(shù)矯正方法，使畸變信號在一定程度上得到了矯正，但該方法仍有一定的缺陷[3]。隨后Johnson等改進(jìn)了此方法，提出了PLL與DFE 算法相結(jié)合的校正方法[4]。國內(nèi)的楊殿閣等研究出一種非線性時(shí)段映射的方式，實(shí)現(xiàn)了在時(shí)域中矯正信號[5]。張翱等利用能量重心法的特性，實(shí)現(xiàn)了多普勒畸變的矯正，在一定程度上提高了診斷精度[6]。

多普勒校正的關(guān)鍵在于對原信號進(jìn)行重采樣，獲得重采樣時(shí)間序列，通過瞬時(shí)頻率估計(jì)方法可解決此關(guān)鍵[7]。目前使用最多的瞬時(shí)頻率估計(jì)方法大致有3種，分別是：STFT譜峰搜索法、隱馬爾科夫模型方法、分段最小二乘擬合方法。但這幾種常用的算法都有其各自的缺點(diǎn)，如進(jìn)行STFT譜峰搜索的瞬時(shí)頻率時(shí)，采用了遮隔技術(shù)，大大增加了計(jì)算量，除此以外，還需提高頻率分辨率。隱馬爾科夫模型瞬時(shí)頻率估計(jì)方法須采用大量的矩陣運(yùn)算，運(yùn)算量也較為復(fù)雜[8]。分段最小二乘擬合算法是根據(jù)在分段點(diǎn)位置判斷是否為速度瞬變點(diǎn)來設(shè)定邊界條件[9]。因此這幾種常用的算法都有其各自的局限性。

由于STFT譜峰搜索法常應(yīng)用在實(shí)際中，針對STFT譜峰搜索法所存在的計(jì)算量大且頻率估計(jì)精度低等問題，本文提出一種基于自動搜峰和shannon熵的滾動軸承多普勒畸變故障聲信號校正方法。首先對所采集的聲音信號進(jìn)行STFT時(shí)頻分析；然后利用自動搜峰方法進(jìn)行瞬時(shí)頻率估計(jì)，設(shè)置shannon熵來提高瞬時(shí)頻率估計(jì)精度，并得到擬合的瞬時(shí)頻率曲線，進(jìn)而得到信號重采樣時(shí)間點(diǎn)；最后對原信號進(jìn)行時(shí)域重采樣，從而使畸變信號得以矯正。

1 多普勒效應(yīng)

在傳聲器采集過程中，由于車輛基本勻速行駛，因此軸承聲源的速度v可以近似看作是恒定的，如圖1所示。由于軸承聲源與傳聲器之間有一段的距離，從而造成傳聲器采集到的頻率發(fā)生了改變，使信號在頻域中發(fā)生頻帶展拓及頻移，即道旁多普勒信號畸變。

圖1 運(yùn)動模型示意圖

在車輛行駛時(shí)，雖然車輛有多個(gè)軸承，但本文把整個(gè)車輛滾動軸承聲源看作單聲源。根據(jù)莫爾斯聲學(xué)理論，傳聲器處采集到的聲壓P為傳播距離衰減的聲場輻射項(xiàng)C與近場效應(yīng)D之和[10]，即：

P=C+D

(1)

其中：

(2)

(3)

其中:q單位時(shí)間內(nèi)流過的物質(zhì)的質(zhì)量，q'=?q/?t，t為聲源運(yùn)動時(shí)刻，θ為聲源運(yùn)動方向與聲源和傳聲器連線之間的夾角，R(t)為t時(shí)刻軸承聲源與傳聲器之間的距離，c為聲速，v為聲源的移動速度，M=v/c為馬赫數(shù)。

由于D值較小，可以忽略不計(jì)。因此采集到的聲壓為：

(4)

等號左右兩邊對相位進(jìn)行求導(dǎo)，整理后可得出頻偏率w。

(5)

式中，x為t=0時(shí)刻時(shí)聲源位置與傳聲器位置水平距離，r為傳聲器到聲源的垂直距離，f0為聲源信號頻率，f為傳聲器采集到的信號頻率。由式(5)可以看出頻偏率隨時(shí)間非線性變換，傳聲器所采集的信號存在多普勒畸變。

2 校正理論與瞬時(shí)頻率估計(jì)方法

2.1 基于瞬時(shí)頻率的多普勒畸變校正原理

目前對多普勒畸變校正較多采用瞬時(shí)頻率估計(jì)方法。在多普勒畸變信號中，假設(shè)原信號只存在f0頻率，原信號的瞬時(shí)頻率與采樣頻率存在如下關(guān)系[11]:

(6)

式中，fs為原信號采樣頻率，fsi為畸變信號i點(diǎn)處的采樣頻率，fi為畸變信號i點(diǎn)處的瞬時(shí)頻率[12]。

根據(jù)采樣間隔和采樣頻率的關(guān)系，即fs=1/dt，代入上式可得:

fi*dti=f0*dt=consti=1,…,N-1

(7)

式中，dti即為重采樣時(shí)間間隔，重采樣時(shí)間點(diǎn)為重采樣時(shí)間間隔之和，即:

(8)

由于當(dāng)重采樣時(shí)間點(diǎn)達(dá)到畸變信號的時(shí)間點(diǎn)即可，所以定義最大重采樣時(shí)間點(diǎn)tM,該值應(yīng)滿足的條件為：

(9)

(10)

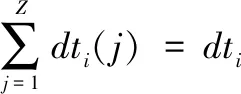
對任意區(qū)間內(nèi)的Z個(gè)時(shí)段求和得：

(11)

可以發(fā)現(xiàn)，當(dāng)Z越大時(shí)，上式可以變?yōu)椋?/p>

(12)

對上式進(jìn)行求解，然后再通過三次樣條插值便可得到矯正信號。

y=[y(ti(1))y(ti(2)) …y(ti(M))]

(13)

2.2 自動搜峰和shannon熵的瞬時(shí)頻率估計(jì)

經(jīng)研究，自動搜峰方法可以解決STFT譜峰搜索法存在的計(jì)算量問題，shannon熵可以提高瞬時(shí)頻率估計(jì)精度。本文通過自動搜峰與shannon熵相結(jié)合進(jìn)行瞬時(shí)頻率估計(jì)。首先利用STFT局部平穩(wěn)特性，從最低頻率到最高頻率進(jìn)行局部自動搜峰，然后設(shè)置shannon熵提高瞬時(shí)頻率估計(jì)精度。自動搜峰和shannon熵的瞬時(shí)頻率估計(jì)流程如圖2所示。

圖2 自動搜峰和shannon熵的瞬時(shí)頻率估計(jì)

具體步驟如下：

1)在STFT時(shí)頻圖上，把總時(shí)間平均分成N份，把頻率長度平均分成 M份，以采集時(shí)刻tNB=0為起點(diǎn)，令fm=kfi，fm為頻率搜索參考峰值，k為加權(quán)因數(shù)，也設(shè)置為N份。同時(shí)k可以控制頻率點(diǎn)數(shù)；

2)對tNB時(shí)刻這一列的頻率進(jìn)行自動分段，即從最低頻率到最高頻率依次開始，當(dāng)出現(xiàn)連續(xù)f(tNB,mi)≥fm時(shí)，搜索出Q個(gè)頻段[13]，即，

Pj(tNB,hkj)=f(tNB,mi)

(14)

式中:Pj(tNB,hkj)為第j個(gè)聲源分量所包含的頻率數(shù)組；hkj=1,L,kj；kj為聲源分量瞬時(shí)頻率寬度，j=1,…,QQ為頻帶個(gè)數(shù);

i=1,…,l1,l1+1,…l1+k1-1,…,l2,l2+1,…,

l2+k2-1,,…,lQ,lQ+1,…,lQ+kQ-1

(15)

3)依次對每一個(gè)聲源頻率數(shù)組Pj(nNB,hkj),j=1,…,Q，分別進(jìn)行峰值搜索，得到相應(yīng)的最大頻率值。由于shannon熵可以衡量信息的價(jià)值，熵越大，不確定性越大，信息量越大[14]。因此可設(shè)置shannon熵來提高瞬時(shí)頻率的估計(jì)精度，具體算法為:

(16)

其中：argmax表示取最大值；Pj(tNB,mMj)為最大頻率峰值；H為shannon熵校準(zhǔn)。

4)從tNB時(shí)刻，改變時(shí)間tg，向右側(cè)重復(fù)步驟2)逐列進(jìn)行自動搜峰，得到所有時(shí)間列的聲源頻率帶寬。Pj(tNB,hkj)為第g個(gè)時(shí)間列中，第j個(gè)聲源分量所包含的頻率數(shù)組；hkj=1,…,kj;kj為聲源分量瞬時(shí)頻率寬度，g=1,NB-1,NB+1,…,N;j=1,…,Q。

5)對每一個(gè)聲源帶寬頻率，分步進(jìn)行峰值搜索，具體算法為：

(17)

其中：arg max 表示取最大值；Pj(tNB,mMj)為最大頻率峰值；H為shannon熵校準(zhǔn)。

2.3 基于自動搜峰和shannon熵的多普勒畸變信號校正方法

基于自動搜峰和shannon熵的多普勒畸變信號校正方法如圖3所示。

圖3 多普勒畸變信號校正流程圖

具體步驟如下：

1)STFT時(shí)頻及頻偏率分析。通過STFT時(shí)頻譜，確定出步驟2)所需求的頻率搜索參考峰值fm。通過頻偏率分析，確定加權(quán)因數(shù)k的范圍。

2)運(yùn)用基于自動搜峰和shannon熵瞬時(shí)頻率估計(jì)。由2.2節(jié)所述方法，獲得所估計(jì)的所有聲源的瞬時(shí)頻率；

3)最小二乘法非線性擬合。對所得的離散瞬時(shí)頻率進(jìn)行非線性插值擬合，得到瞬時(shí)頻率擬合值；

4)時(shí)域重采樣。通過擬合后的瞬時(shí)頻率計(jì)算出重采樣的時(shí)間點(diǎn)，從而消除多普勒畸變；

5)判斷還原的信號是否校正。通過頻域分析確定信號是否校正，若信號未能校正，則調(diào)整頻率搜索參考峰值，重新進(jìn)行瞬時(shí)頻率估計(jì)。

6)頻域分析。在頻域中分析校正的信號來驗(yàn)證本文方法的可行性。

3 仿真驗(yàn)證

3.1 仿真試驗(yàn)

本文運(yùn)用matlab軟件創(chuàng)建仿真試驗(yàn)。為更好突出多普勒畸變效果，仿真3個(gè)聲源信號，頻率為f1=100 Hz，f2=200 Hz，f3=300 Hz。設(shè)定采樣頻率為10.24 kHz，設(shè)置仿真參數(shù)x=10 m,r=1 m,c=340 m/s,以及v=10 m/s，信噪比為5 dB。由于多普勒信號畸變在頻域中突出，因此本文重點(diǎn)在頻域分析。仿真的原信號如圖4和圖5所示。

圖4 仿真的原信號頻譜圖 圖5 仿真的原信號STFT圖

3.2 結(jié)果分析

由圖4可以看出仿真的多普勒畸變原始信號頻率發(fā)生了頻移，100 Hz的頻率移動至60.3 Hz，200 Hz的頻率移動至121.3 Hz，300 Hz的頻率移動至181.9 Hz，同時(shí)200 Hz的頻率和300 Hz的頻率也發(fā)生了頻帶展拓。由圖5和圖6可以看出瞬時(shí)頻率隨時(shí)間連續(xù)變化。在時(shí)刻t=0時(shí)，100 Hz頻率出現(xiàn)在103 Hz處，因此搜索算法中設(shè)定103 Hz 為起始點(diǎn)，設(shè)定加權(quán)因數(shù)k為1.03-0.97(由頻偏率圖可知)，再通過自動搜峰和shannon熵的瞬時(shí)頻率估計(jì)得到各段對應(yīng)的瞬時(shí)頻率。把序列自動分為512段(由計(jì)算速度和收斂性確定)，如圖7為序列的shannon熵值。

圖6 仿真的原信號頻偏率 圖7 shannon熵校準(zhǔn)

由于shannon熵在值為6.5處發(fā)生突變且大多數(shù)信號序列的shannon熵值大于6.5，因此選取shannon熵大于6.5的數(shù)據(jù)點(diǎn)。得到瞬時(shí)頻率后，進(jìn)行非線性最小二乘法擬合，其瞬時(shí)頻率擬合圖如圖8 所示。擬合函數(shù)中有6個(gè)未知量，即f1，f2，f3，r，v，x。如表1為將仿真參數(shù)值與擬合值的相對誤差。

圖8 瞬時(shí)頻率擬合圖

仿真值擬合值相對誤差/%f1/Hz100100.00010.0001f2/Hz2002000f3/Hz3003000x/m10100v/(m?s-1)1010.00010.001r/m10.99860.14

最后，采用本文提出的信號畸變校正方法。由圖9和圖10所示，可以清晰地看出，所設(shè)置的頻率均得到了還原，而且從表1可以看出各參數(shù)的誤差均很小，都在誤差范圍之內(nèi)，從而驗(yàn)證了本文所提出的多普勒畸變校正方法的可行性。

圖9 重采樣后頻域圖 圖10 重采樣后的STFT圖

4 試驗(yàn)驗(yàn)證

為有效驗(yàn)證本文方法的可行性，本文利用電動車運(yùn)載聲源形成多普勒效應(yīng)。如圖11(a)所示，聲源是利用錄音筆從軸承型號為SKF 6016的試驗(yàn)臺錄制而成，設(shè)置靜止實(shí)驗(yàn)臺軸的轉(zhuǎn)速為114 r/min(對應(yīng)實(shí)際車輛36 km/h車速)。實(shí)驗(yàn)臺所用的滾動軸承的內(nèi)徑為80 mm,外徑為125 mm，滾子直徑為14 mm，滾子個(gè)數(shù)為14，接觸角為0°，軸承寬度為22 mm。

根據(jù)軸承故障特征頻率計(jì)算公式，可以得出理論的內(nèi)圈故障特征頻率應(yīng)為15.1 Hz。具體計(jì)算的內(nèi)圈故障特征特征頻率及倍頻見表2。

表2 滾動軸承內(nèi)圈故障特征頻率及倍頻

如圖11(b)所示，電動車以36 km/h的速度勻速行駛，在前車輪處固定一錄音筆，以播放軸承故障聲音信號。數(shù)據(jù)采集設(shè)備型號為INV3060V，采集軟件為DASP-V10，采樣頻率為10.24 kHz，采樣時(shí)間為5 s，傳聲器與電動車行駛方向垂直距離大約 1 m 左右。由于故障特征頻率三倍頻都小于50 Hz，因此本文在頻域圖中分析的頻率范圍為[0 50]。為了更好地分析信號，本文只分析傳聲器前后1 s采集的信號。

圖11 試驗(yàn)場景

圖12采集到的軸承內(nèi)圈故障信號。在頻域圖中，可以觀察出在內(nèi)圈特征頻率15.1 Hz附近出現(xiàn)了一個(gè)1 Hz的頻帶展拓。而在圖13(a)無法觀察到15.1 Hz頻率，因此從圖12和圖13(a)可以說明采集到的信號發(fā)生了多普勒畸變。圖13(b)為信號序列分為512段的shannon熵值。由于shannon熵值為4.5時(shí)信號序列突變并且大多數(shù)信號序列的shannon熵值大于4.5，因此設(shè)置shannon熵的閾值為4.5。采用本文的瞬時(shí)頻率進(jìn)行頻率估計(jì)，如圖13(c)。

圖12 采集到的軸承內(nèi)圈故障信號

圖13 瞬時(shí)頻率估計(jì)

在圖14(a) 中可以觀察到校正后的信號頻譜中出現(xiàn)了內(nèi)圈故障頻率15.1 Hz，1 Hz的頻帶展拓基本消失，精確度較高。在圖14(b)中也可以觀察到在15.1 Hz附近存在一個(gè)不隨時(shí)間變化的頻率。因此信號處理結(jié)果表明內(nèi)圈故障頻率得到了校正，內(nèi)圈故障多普勒畸變已經(jīng)基本消除。

圖14 軸承內(nèi)圈故障信號重采樣后信號分析

為了體現(xiàn)本文方法的優(yōu)勢，本文將其與傳統(tǒng)STFT搜峰瞬時(shí)頻率估計(jì)方法進(jìn)行比較。設(shè)置傳統(tǒng)STFT搜峰瞬時(shí)頻率估計(jì)參數(shù)與本文方法參數(shù)一致。效果比較見圖15及表3。從圖15(a)可以觀察到利用傳統(tǒng)STFT搜峰瞬時(shí)頻率估計(jì)方法還原的頻率為15 Hz,在圖15(b)中的1 s到1.5 s之間15 Hz頻率的頻帶發(fā)生了錯位，因此精確度一般。從表3可以看出，本文所用方法在瞬時(shí)頻率用時(shí)、自適應(yīng)性及準(zhǔn)確度方面都具有一定的優(yōu)勢。

圖15 傳統(tǒng)方法的軸承內(nèi)圈故障信號重采樣后信號分析

本文方法傳統(tǒng)方法是否需要遮隔方法不需要需要瞬時(shí)頻估計(jì)用時(shí)193s376s是否具有自適應(yīng)性有自適應(yīng)性無自適應(yīng)性精確度較高一般

5 結(jié)束語

本文提出一種基于自動搜峰和shannon熵的滾動軸承多普勒畸變故障聲信號校正方法。通過對仿真信號分析，可以看出該方法的誤差在容許的范圍內(nèi)。通過試驗(yàn)結(jié)果分析，重采樣后的內(nèi)圈故障信號頻譜中出現(xiàn)了內(nèi)圈故障特征頻率，在重采樣后的STFT圖中也可以觀察到內(nèi)圈故障頻率得到了校正。因此該方法可應(yīng)用于基于道旁聲學(xué)的車輛軸承故障診斷中。同時(shí)與傳統(tǒng)STFT搜峰瞬時(shí)頻率估計(jì)方法相比，本文所用方法在瞬時(shí)頻率用時(shí)、自適應(yīng)性及精確度方面都具有一定的優(yōu)勢。