擋土墻上被動土壓力的變分求解方法

趙國，陳建功

(重慶大學 土木工程學院；山地城鎮建設與新技術教育部重點實驗室，重慶 400045)

被動土壓力的計算是擋土墻上土壓力理論研究內容之一，除了對經典的朗肯土壓力理論和庫侖土壓力理論進行擴展、補充外，學者們在考慮其他諸如土拱效應、強度理論、位移模式等方面也對被動土壓力的計算進行了深入探討。李永剛[1]、王立國等[2]考慮了土拱效應原理，按庫侖理論得到土壓力強度的計算方法。侯鍵等[3]對平移模式下剛性擋土墻和滑裂面間處于被動極限平衡狀態的楔形土體進行應力分析，推導了基于土拱原理的被動土壓力系數和滑裂面水平傾角,并提出被動土壓力分布、土壓力合力及其作用位置公式。Chang[4]、蔣波等[5]和楊泰華等[6-9]對不同變位模式下的非極限主動土壓力進行計算，提出考慮位移效應的被動土壓力計算理論。程康等[10]推導了平動模式下非飽和土填土擋墻的被動土壓力系數及被動土壓力解析解。趙均海等[11]考慮基質吸力等因素的影響，結合雙剪強度理論，建立了非飽和土庫侖被動土壓力的統一解。

變分極限平衡法最早是由Kopácsy提出的[12-14]。李興高、劉維寧等[15-17]基于墻后滑楔體整體極限平衡方程，建立了被動土壓力計算的泛函極值模型，計算結果表明,擋墻背后土體存在兩種被動臨界狀態，兩種狀態的計算結果就是被動土壓力大小的一個區間估計。該方法所建模型為填土面水平、墻背垂直的情況，不能用于一般情況。對于承受被動土壓力的擋土墻(如橋臺)，有必要研究合力作用點位置對被動土壓力大小的影響，本文考慮在一般情況下(傾斜墻背，填土表面非均勻堆載,墻后為黏性土體，坡面為曲面)，利用變分法原理，提出基于合力作用點位置的被動土壓力計算方法，由此可以得到擋墻被動土壓力的大小和作用點位置的范圍。

1 被動土壓力變分計算模型

設擋土墻高為H，坡面形狀為y=g(x)，傾斜角為α，墻后土體容重為γ，墻土間的摩擦角為δ，黏聚力為c、內摩擦角為φ，q(x)為作用在坡面上的豎向壓力集度。考慮極限平衡條件下墻后土體形成滑動楔體，假定其滑裂面通過擋墻墻踵，用曲線y=s(x)表示，Pp為擋土墻對滑動土體的作用合力，其值等于被動土壓力合力。σ(x)、τ(x)為滑裂面上的法向和切向應力，點B為滑裂面的上端的點，其X坐標為x1，A為墻背的上端點，其X坐標為x2點，x2=-tanα，被動土壓力作用點位置至墻踵的垂直距離與擋土墻高度的比值稱為作用點位置系數ξ，見圖1。滑楔體OAB的靜力平衡方程為

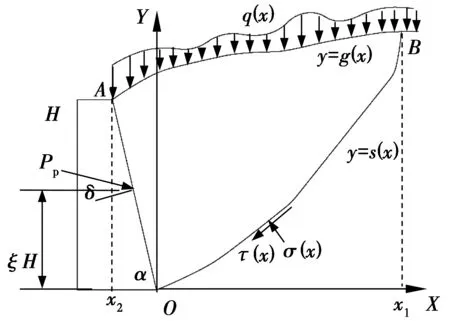
圖1 計算模型示意圖Fig.1 Sketch map of computation

由∑X=0得

(1)

由∑Y=0得

(2)

由∑MO=0得

qx+(g-s)γx]dx=0

(3)

式中：s′=ds/dx；k=tanα，滑裂面上的應力遵循Mohr-Coulomb 破壞準則，即

τ=n1σ+c

(4)

式中：n1=tanφ。

由式(1)～式(3)，可建立相應的泛函極值模型。

由式(3)得泛函

(5)

式中：

F0=(x+ss′+n1s-n1s′x)σ-(g-s)γx-s′xc+sc-qx；

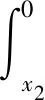
由式(1)得約束條件

(6)

式中：

F1=(-n1-s′)σ-c；

z2=z0z1=const。

由式(2)得約束條件

(7)

式中：

F2=(-n1s′+1)σ-cs′-q-γ(g-s)；

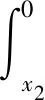
上述模型是變分學中的等周模型，可轉化為無約束泛函極值模型，構造泛函J*。

(8)

F=F0+λ1F1+λ2F2

式中：λ1、λ2為拉格朗日乘子。變分模型的歐拉微分方程、邊界條件及可動邊界處的橫截條件為

1)Euler微分方程

(9)

(10)

2)約束方程

同式(6)、式(7)。

3)邊界條件

s(0)=0

(11)

s(x1)=g(x1)

(12)

4)橫截條件

(13)

2 被動土壓力變分計算模型的求解

由式(9)，可得到

(14)

進行坐標平移，引入新坐標

u=x+λ2，v=s-λ1

(15)

坐標平移后的模型見圖2。

圖2 坐標變換后的計算模型Fig.2 Computation model after coordinate

令w=v/u，則微分方程式(14)變為

(16)

分離變量得通解為

ln[u2(1+w2)]=2n1arctanw+z5

(17)

平移后的坐標換成極坐標

u=rcosθ，v=rsinθ

(18)

式(17)變為

r=z6en1θ

(19)

式中：z5、z6為任意積分常數。

由s(0)=0得原坐標原點O在新坐標中為u0=λ2，v0=-λ1，新坐標中O點的極坐標為(r0,θ0)，則滑裂面方程為

r=r0e-n1(θ0-θ)

(20)

滑裂面為對數螺旋面。

由式(10)得

-2n1σ+(-n1x+s-λ1-n1λ2)σ′-

γx-λ2γ-2c=0

(21)

式(21)在新坐標下的極坐標形式為

(22)

式(22)的通解為

式中：z7為積分常數；θ1為任意角度，可取θ1=0。

σ=z7e-2n1θ-

(23)

由式(13)可得A點處正應力為

σ(x1)=σ(θ1)=

(24)

將式(24)代入式(23)，得

z7= e2n1θ1·

上述變分問題只包含兩個未知的拉格朗日常數λ1、λ2，可由式(6)和式(7)聯立求出，相當于求式(25)函數Φ的零值問題。

(25)

式(25)的解可通過求解函數Φ的極小值且極小值為0得到，可采用Matlab提供的Fminsearch函數進行求解。

3 算例分析

設擋土墻墻高6 m，墻后為砂土，重度γ=18 kN/m3，內聚力c=0，內摩擦角φ=30°，擋土墻傾角α=70°，擋墻與土體的摩擦角δ=10°，坡面傾角β=20°，上部堆載q=10 kPa。

計算結果見圖3，圖中Φ曲線存在一Φ=0的水平直線段，此直線段的ξ系數變化范圍就是被動土壓力合力作用點的位置系數范圍，存在上下界限值(此例中下限值ξd=0.336 9，上限值ξu=0.535 5)，在此范圍內，Φ=0，也即是說，當土壓力的合力作用點位于距墻鍾2.02～3.21 m范圍內時，墻后土體可以達到極限平衡狀態。圖4為被動土壓力合力隨作用點位置系數ξ的變化曲線，圖5為滑裂面隨作用點位置系數ξ的變化情況。隨著作用點位置系數的增大，被動土壓力呈非線性增長，在作用點位置下限處，被動土壓力最小，滑裂面為對數螺旋曲面，但隨著作用點位置的上移，曲率半徑逐漸增大，到上限處變為平面，此時，被動土壓力值達到最大。

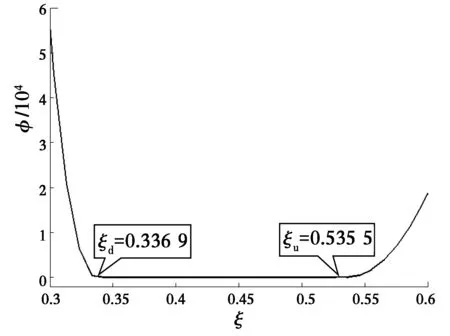
圖3 Φ函數計算結果Fig.3 Calculated result of function Φ

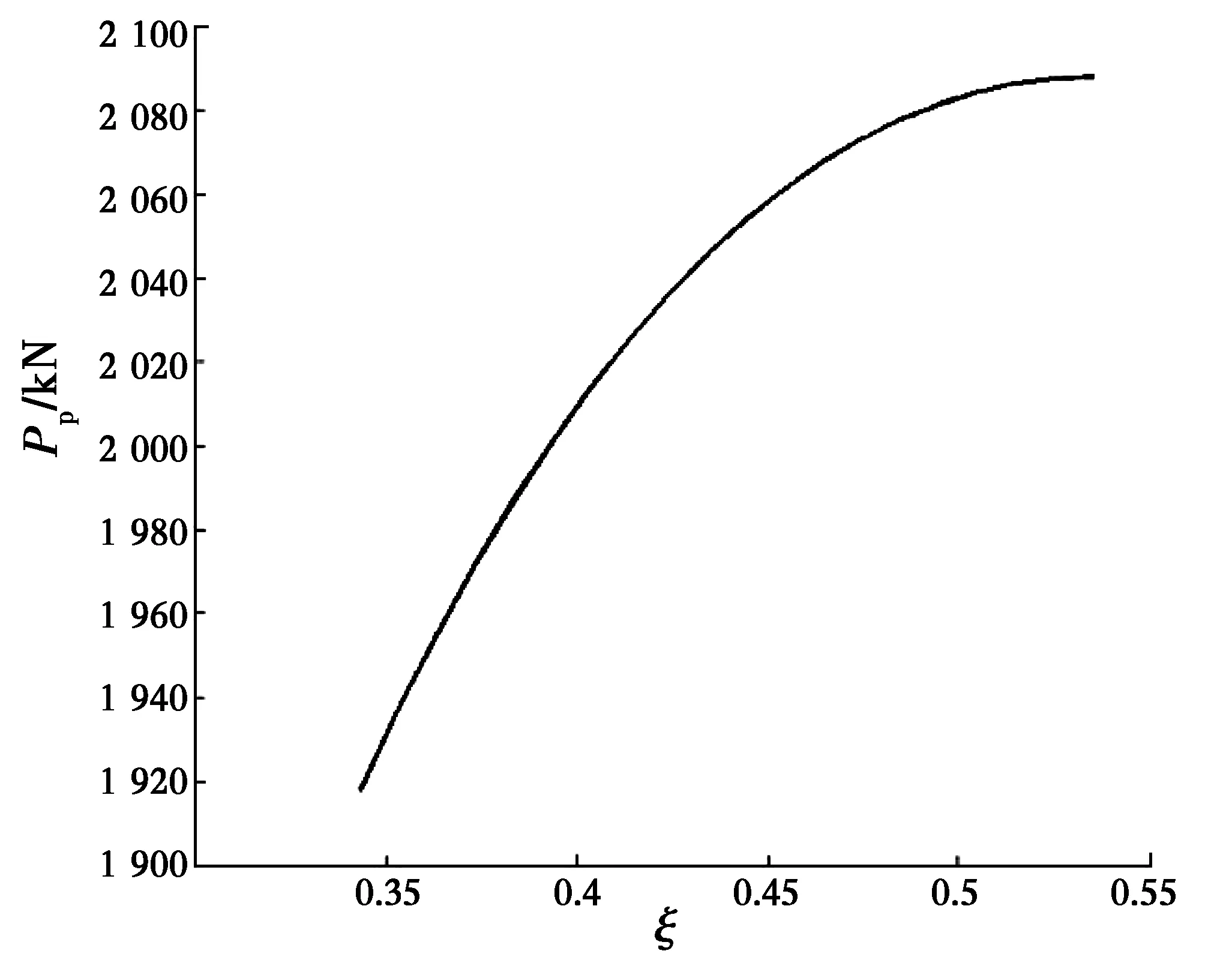
圖4 被動土壓力隨系數ξ的變化曲線Fig.4 The curves of varied passive pressure according the coefficient ξ

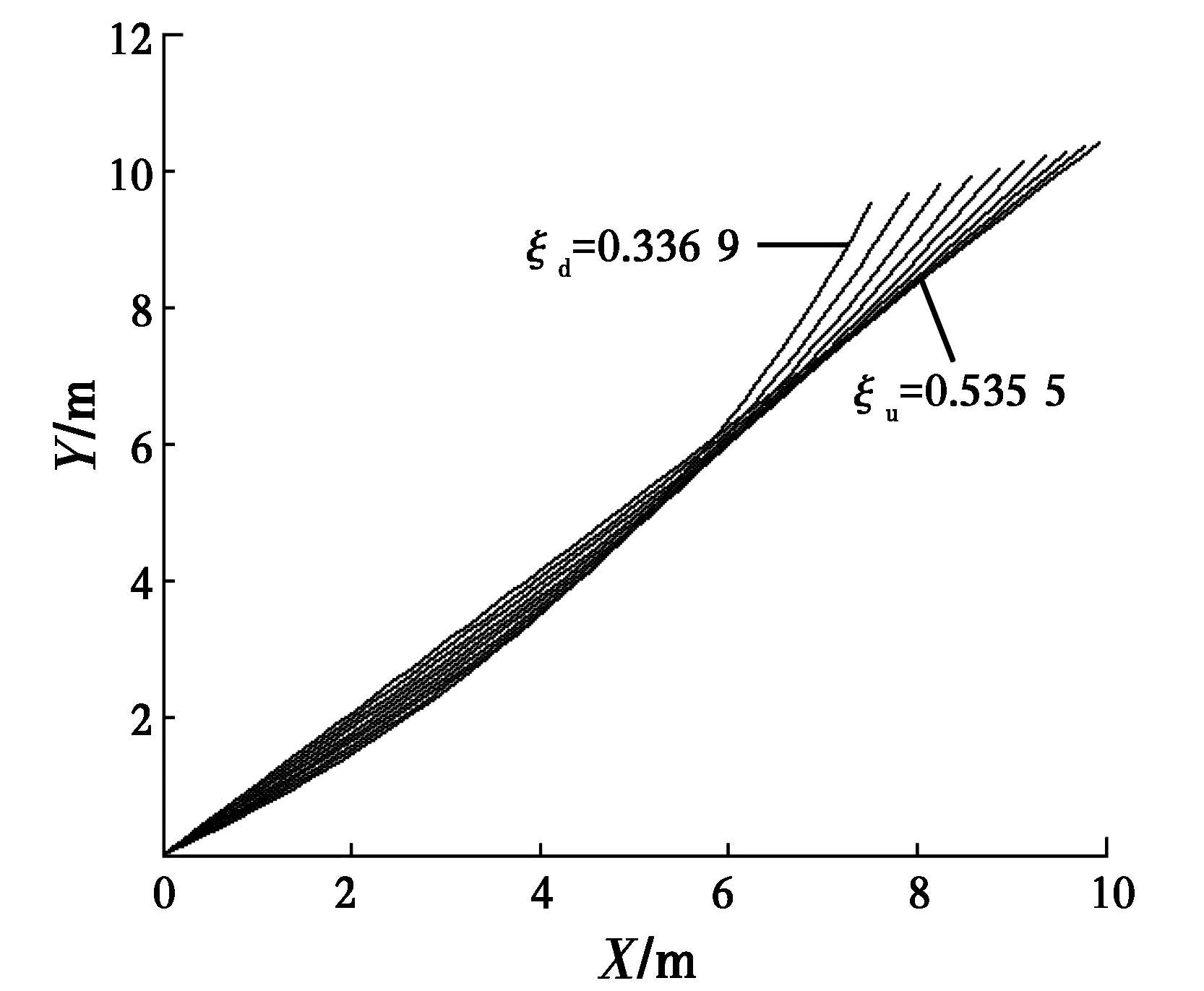
圖5 不同ξ對應的不同滑裂面曲線Fig.5 The different curves of slip face according to different values of

4 與庫侖土壓力理論結果對比

按變分法的計算結果與按庫侖公式的計算結果見表1。可以看出，當作用點位置在上界限時，即滑裂面為平面時，被動土壓力值與按庫侖公式得到的土壓力值是一致的，但合力作用點位置卻不一致，這主要是因為庫侖理論假定土壓力線性分布，且不考慮土楔體力矩平衡條件。按變分法的計算結果，當滑裂面為平面時，滑裂面上的應力分布呈非線性，相應的土壓力分布也應是非線性的。

表1 變分法與庫侖土壓力理論的計算結果比較Table 1 Result comparing of passive earth pressure using variational method and using Coulomb theory

圖6所示為庫侖理論的擋土墻模型，取墻后部分三角形滑動土楔體ABD作為研究對象，如圖7所示。Pp(y)為墻背對滑楔體的支撐反力合力，也即被動土壓力合力；R(y)為不動土體對滑楔體的反力合力；G(y)為土體ABD的重量；Q(y)為作用在AD面上豎向壓力。

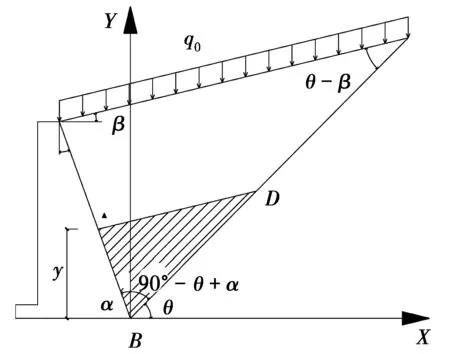
圖6 庫侖剛性擋土墻模型圖Fig.6 COULOMB’s Model of retaining

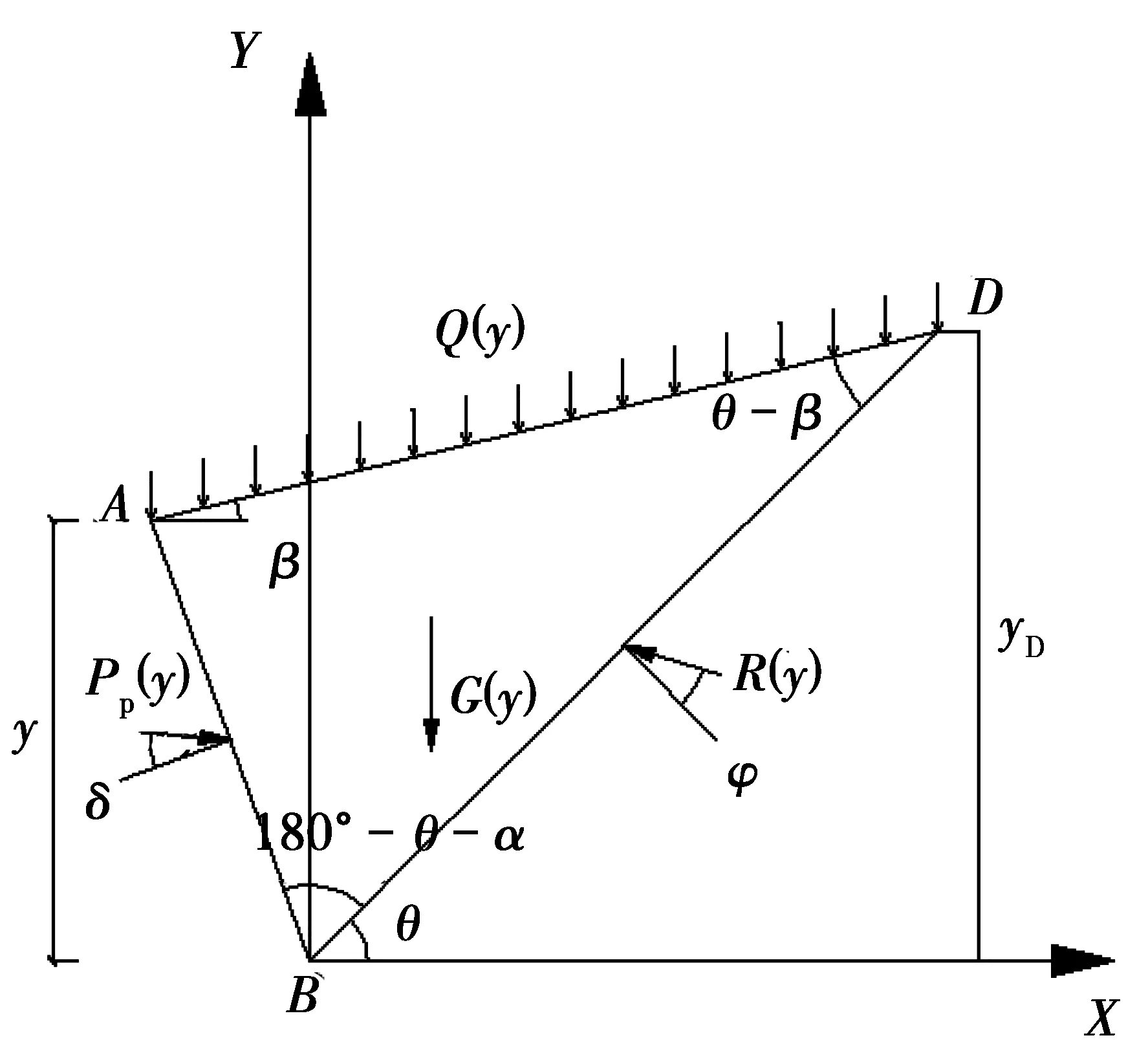
圖7 土楔體ABD受力分析Fig.7 mechanical analysis on sliding wedge

土楔體ABD的力平衡條件見圖8，由三角形正弦定理可得

(26)

令pp(y)為墻背對滑楔體的支撐反力強度，也即被動土壓力強度，r(y)為不動土體對滑楔體的反力強度，即

(27)

將式(27)代式(26)，得

(28)

考慮幾何關系

(29)

式(28)兩邊對y求導，得

(30)

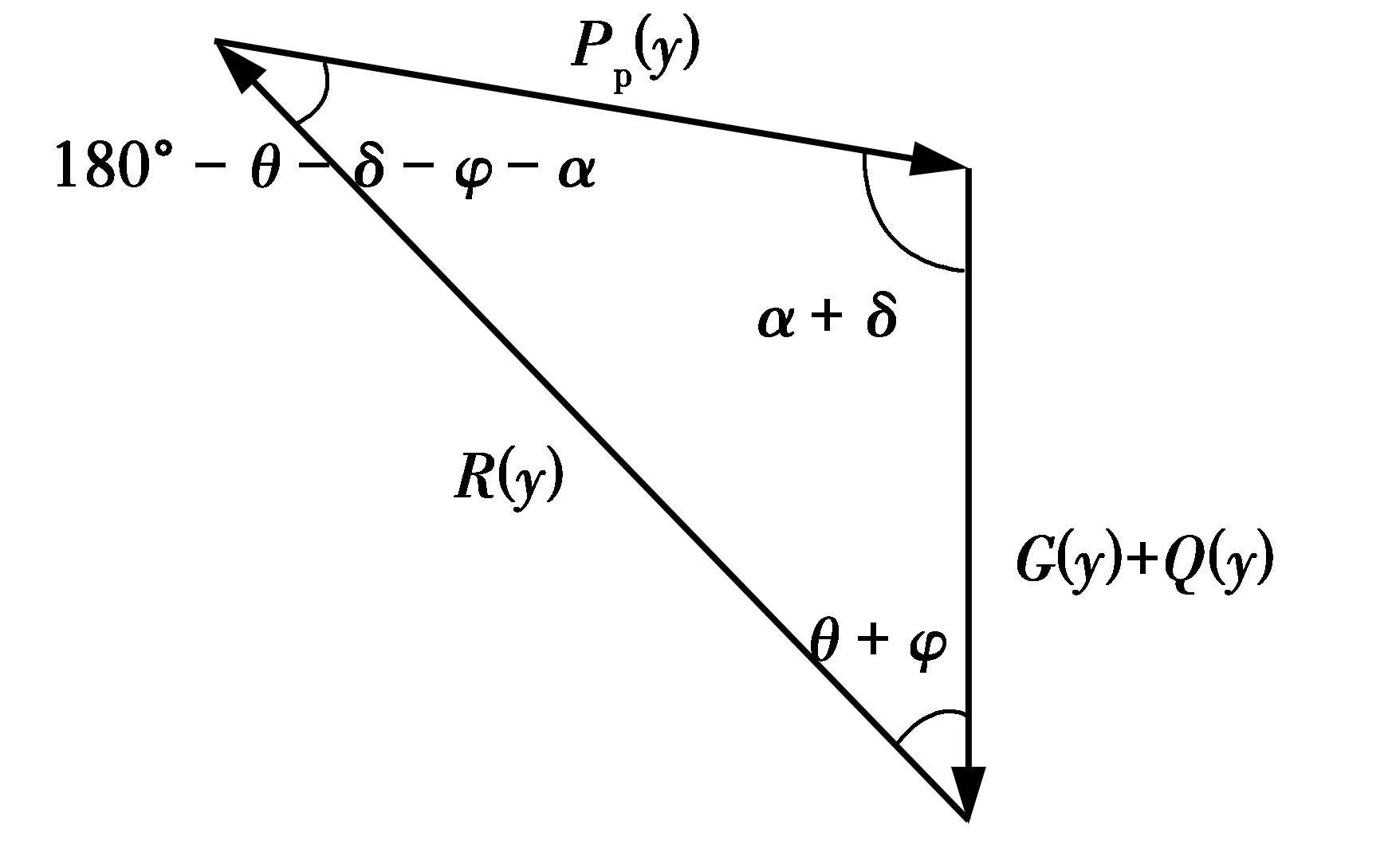
圖8 土楔體ABD的力平衡條件Fig.8 Force equilibrium of sliding wedge

圖9 土壓力強度分布圖Fig.9 Distribution of earth

表1中的安全系數一欄是指按庫侖公式進行擋墻的抗傾覆設計，取1.5的安全系數時所對應的按本文方法計算的抗傾覆安全系數范圍。若按庫侖理論進行設計，實際的被動土壓力合力作用點位置比庫侖理論設定的要高，其安全系數達不到1.5的要求，所以，應優化擋墻的結構，控制擋墻的變位模式，使合力作用點降低，提高抗傾覆安全系數。

5 坡面起伏和非均勻超載對被動土壓力的影響

設擋墻高6 m，墻后土重度γ=18 kN/m3，內聚力c=10 kPa，內摩擦角φ=20°，擋土墻傾角α=70°， 坡面形狀函數g(x)和非均勻超載q(x)均用三角函數模擬坡面的起伏和非均勻超載。表2為計算結果，可以看出，被動土壓力合力和作用點受坡面的起伏以及坡面超載的不均勻性影響不能忽視。

表2 考慮坡面起伏及非均勻超載的計算結果Table 2 Computed results considering surface undulation of earth filling and uneven surface load

6 結論

基于墻后滑楔體整體極限平衡方程，利用變分法原理推導了被動土壓力泛函極值的變分模型，提出了相應的計算方法，當作用點位置已知時，可有效確定被動土壓力大小和滑裂面形狀位置。算例分析表明，墻后土體的極限平衡狀態對應于作用點位置系數范圍，隨著作用點位置系數的增大，被動土壓力呈非線性增長，在作用點位置下限處，被動土壓力最小，滑裂面為對數螺旋曲面，但隨著作用點位置的上移，滑裂面曲率半徑逐漸增大，到上限處變為平面。此時，被動土壓力值達到最大，且與按庫侖理論計算的被動土壓力一致，但作用點位置位于墻背中點以上，與庫侖理論所假定的合力作用點位置不一致。