鋼骨-組合L形鋼管混凝土柱的軸壓承載力

王博， 趙均海， 張冬芳， 馬康凱

(長安大學 建筑工程學院，西安 710061)

鋼管混凝土柱憑借其較高的承載力以及良好的抗震性能，越來越多地應用于建筑結構中。隨著研究的不斷深入，為了使不同位置柱的布置更加合理，提出了異形鋼管混凝土柱(T形、L形、十字形)[1-3]。異形鋼管混凝土柱采用邊柱T形、角柱L形、中間柱十字形的方式廣泛應用于中高層建筑結構，此類布置方式能有效避免柱陰陽角的出現，提高建筑的使用面積。隨著現代結構向大跨度、大開間、重載方向發展，為提高異形鋼管混凝土柱的承載力，提出將異形鋼管混凝土柱中內置型鋼鋼骨組成內置鋼骨的異形鋼管混凝土柱，兩者的結合將更加有效地發揮各自的特點。

學者們已經對異形截面鋼管混凝土柱軸壓性能進行了大量研究。Xiong等[4]對通過垂直雙鋼板連接的L形鋼管混凝土柱進行了軸壓試驗，研究了柱的破壞模式、荷載-變形關系、應變分布、延性和強度指標；陳雨等[5]對T形鋼管混凝土短柱進行了軸壓試驗研究，考察了無加勁措施T形鋼管混凝土柱的變形特征、破壞模式和承載能力；Chen等[6]對6組L形鋼管混凝土短柱和一組L形鋼管空心短柱進行了軸壓試驗，描述了試件的非線性損傷過程和破壞模式，進行了結構參數對承載力的影響研究；雷敏等[7]基于單雙向偏心受壓試驗結果，建立了纖維模型程序，分析其承載力的本構模型，在驗證本構模型合理性的基礎上，對T形鋼管混凝土柱軸壓穩定性能進行了參數研究。以上對異形鋼管混凝土柱軸壓承載力的研究表明異形鋼管混凝土柱的合理性與適用性，但陰角易發生屈曲，重載下延性不足，混凝土斜裂縫的產生使得外包鋼管對核心混凝土約束下降等問題依舊未得到解決，從而提出了內置鋼骨的組合異形鋼管混凝土柱。目前，對于內置鋼骨的組合異形鋼管混凝土柱軸壓承載力研究，能夠查閱到的研究文獻還比較有限，宋鑫[8]通過對內置鋼骨的組合L形截面鋼管混凝土短柱軸心受壓試驗，研究了其破壞形態、荷載-位移曲線特征、各參數對其軸壓力學性能的影響。杜國鋒等[9-10]在試驗基礎上考慮鋼管對核心混凝土的約束效應，依據數據擬合，提出了內置鋼骨L形、T形鋼管混凝土短柱的承載力公式。對于內置鋼骨的組合異形鋼管混凝土柱軸壓承載力，部分研究主要以試驗為主，所提出的承載力公式大多是從試驗數據回歸分析或簡化計算得到，理論依據不夠明確，不具備推廣性；而部分研究所提出的承載力計算公式[10]，在考慮鋼管對混凝土的約束時,未合理考慮組合異形截面鋼管的約束效應，同時，未考慮核心混凝土側向約束對中心鋼骨抗壓強度提高的影響。

鑒于以上研究中存在的問題，本文以內置鋼骨的組合L形鋼管混凝土柱為研究對象，將組合L形短柱分為一個矩形鋼管和一個方形鋼管。考慮寬厚比對鋼管縱向應力及環向應力的影響，將鋼管長短邊非均勻約束等效為環向均勻約束，引入混凝土強度折減系數，考慮側向約束折減。基于統一強度理論，分別推導核心混凝土和鋼骨的承載力公式，并建立鋼骨-L形鋼管混凝土短柱軸壓承載力計算式。在此基礎上，參考鋼結構設計規范，提出軸壓中長柱的承載力計算公式，為鋼骨-組合L形鋼管混凝土柱軸壓承載力提供了理論依據。

1 統一強度理論

統一強度理論是俞茂宏[11]在1991年提出的，考慮了中間主應力對材料破壞的影響，適用于各種不同材料。具有簡單而統一的數學表達式，清晰合理的物理概念和統一的力學模型，能夠吻合學者們所得出的不同材料的大量試驗結果，其數學表達式為

(1a)

(1b)

(2)

式中：F、F′為主應力強度理論函數；σ1、σ2、σ3分別為3個主應力；σt、σc、τs分別為材料的拉伸、壓縮、剪切屈服應力；α為材料拉壓強度比；b為反映中間主切應力以及相應面上的正應力對材料破壞影響程度的系數。

2 鋼骨-組合L形鋼管混凝土短柱軸壓承載力計算

2.1 鋼骨-組合L形鋼管混凝土短柱軸心受壓破壞機理

鋼骨-L形鋼管混凝土柱在軸壓狀態下，鋼管、混凝土與鋼骨共同承擔軸向荷載作用。杜國鋒等[10]試驗研究表明，在加載初期，鋼管對核心混凝土的約束較小，鋼管、混凝土與鋼骨均處于各自單獨工作的彈性階段。隨著軸向壓力的不斷增大，鋼管和鋼骨縱向應變、鋼管橫向應變呈非線性增長，此時，鋼管處于軸向受壓、環向受拉狀態。混凝土的橫向變形加大，鋼管對混凝土起到約束作用，核心混凝土受到鋼管與鋼骨的雙重套箍作用，處于三向復雜應力狀態下。隨著加載的進行，達到極限荷載時，鋼管和鋼骨的應變開始迅速增長，鋼管對混凝土的約束明顯增強，試件各面微鼓變大，在矩形鋼管的長邊，鋼管局部向外鼓出較其他各邊更為明顯。因此，本文依據軸壓破壞機理，合理考慮鋼管所處應力狀態及對核心混凝土的約束作用，對軸壓短柱極限承載力進行分析。

2.2 鋼管寬厚比對環向及軸向應力的影響

Ge等[12]研究表明，鋼管寬厚比是影響鋼管混凝土試件承載力的主要因素，在軸向壓力作用下，鋼管處于軸向受壓、徑向受壓、環向受拉的三向應力狀態下，而徑向受力相比環向與軸向較小，可忽略其影響。故基于VonMises屈服準則，當R>0.85時(R為鋼管長短邊寬厚比參數)，認為鋼管長邊發生局部屈曲破壞；當R≤0.85時，可不考慮試件局部屈曲。利用文獻[12]的研究成果，考慮在L形鋼管混凝土柱中鋼管寬厚比對環向及軸向應力的影響，計算公式為

(3)

當R>0.85時

(4)

(5)

當R≤0.85時

fa=0.89fy

(6)

fsr=-0.19fy

(7)

式中：B為鋼管邊長；Es、ν為鋼管的彈性模量、泊松比；fa、fsr分別為鋼管軸向抗壓強度、環向抗拉強度。

2.3 鋼管等效側向約束力作用

核心混凝土分為有效約束區和非有效約束區，有效約束區混凝土抗壓強度高于非有效約束區，非有效約束區所受的側向壓力是不均勻的[13]。根據組合L形特點，假定核心混凝土有效約束區的邊界線為二次拋物線，如圖1所示，對有效約束區和非有效約束區進行劃分。

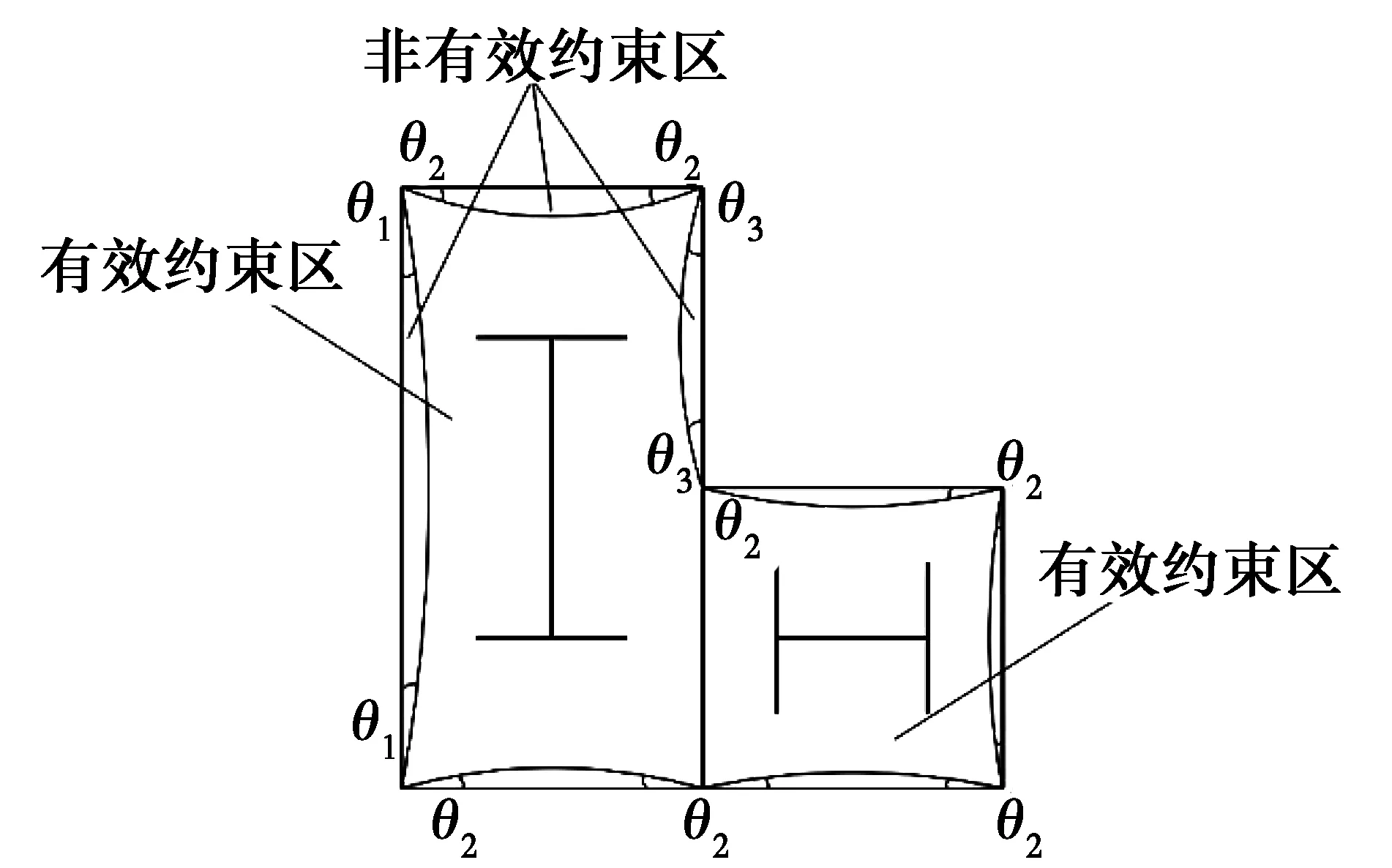
圖1 橫截面核心混凝土有效約束區Fig.1 Effectively confined concrete of

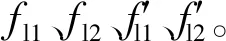
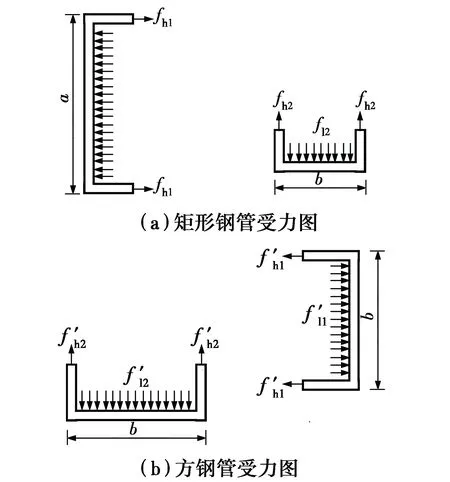
圖2 鋼管受力示意圖Fig.2 Schematic diagram of the force of a steel

由平衡條件，得矩形鋼管約束應力為

(8)

(9)

方鋼管約束應力為

(10)

(11)

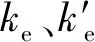
考慮到有效約束區較非有效約束區約束力強，依據面積占比，核心混凝土有效約束系數為

(12)

(13)

式中：θ1、θ2、θ3為約束界限邊切角，考慮到長邊和短邊對核心混凝土的約束作用不同，采用龍躍凌等[15]基于試驗數據所提出的公式。

(14)

(15)

(16)

(17)

(18)

(19)

式中：fy為鋼管的屈服強度；ζ1、ζ2、ζ3分別為θ1、θ2、θ3的約束界限邊切角系數，其中θ1、θ2、θ3的計算公式適用于長寬比a/b為1.0～2.0，寬厚比b/t為20～50的矩形鋼管混凝土。

趙均海等[16]將方形鋼管混凝土柱按面積相等等效為圓鋼管混凝土柱，依據厚壁圓筒理論，在厚壁圓筒環向應力屈服條件下，得到側向約束應力，且承載力公式與試驗數據吻合較好。借鑒文獻[16]中的方法，依據面積等效原則，將矩形混凝土等效成圓形混凝土。同時，按照側向約束力相等原則，考慮鋼管環向應力未達到屈服，將鋼管各邊側向均勻約束等效為圓形鋼管均勻約束，使得核心混凝土處于常三軸受壓應力狀態下，從而使得0>σ1=σ2=σr>σ3。

依據面積等效原則，將矩形混凝土等效成圓形混凝土，故

(20)

依據面積等效原則，將方形混凝土等效成圓形混凝土，得

(21)

式中：t為鋼管壁厚；R1、R2分別為矩形和方形混凝土等效為圓形混凝土的半徑。

可得到

(22)

(23)

依據側向約束力等效原則，可得

(24)

(25)

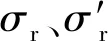
將式(8)、式(9)、式(22)代入式(24)，得

(26)

將式(10)、式(11)、式(23)代入式(25)，得

(27)

考慮環向應力未達到屈服，依據鋼管環向應力式(5)、式(7)，可得

(28)

(29)

將式(28)、式(29)分別代入式(26)、式(27)，得

(30)

(31)

2.4 核心混凝土的軸壓強度

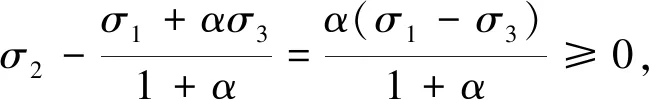
σ3=fc+kσr

(32)

考慮到矩形鋼管約束力不如等效圓鋼管約束力強，引入折減系數γu，得

(33)

(34)

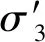
將式(30)、式(31)分別代入式(33)、式(34)，可得

(35)

(36)

2.5 鋼骨承載力

(37)

式中：fst為鋼骨拉伸屈服強度；α為鋼骨材料拉伸強度fst和壓縮強度極限fsc的比值。

公式中取壓為正，拉為負，根據式(37)可得

fs1=σ3=σr+fsc

(38)

(39)

式中：fs1、fs2分別為矩形鋼管鋼骨和方形鋼管鋼骨的抗壓承載力；fsc為鋼骨抗壓強度。

將式(30)、式(31)分別代入式(38)、式(39)，得

(40)

(41)

2.6 L形短柱軸壓承載力計算

組合短柱的軸壓承載力由3部分組成，分別是鋼管縱向承載力、受約束混凝土所提供的承載力以及中心鋼骨所提供的承載力。軸壓短柱承載力公式為

Nu=Nu1+Nu2

(42)

Nu1=fyt1At1+fc1Ac1+fs1As1

(43)

Nu2=fyt2At2+fc2Ac2+fs2As2

(44)

式中:Nu為L形短柱承載力；Nu1、Nu2分別為矩形和方形鋼骨鋼管混凝土短柱承載力；fyt為鋼管壓應力，當短柱達到極限承載力時；At、Ac、As分別為鋼管的承壓面積、混凝土的承壓面積以及鋼骨的承壓面積。fyt按照式(7)、式(9)算得。

將式(5)、式(35)、式(40)代入式(43)，可得

(45)

將式(6)、式(36)、式(41)代入式(44)，可得

(46)

將式(45)、式(46)代入式(42)，可得

Nu=fyt1At1+fyt2At2+Acfc+Asfsc+

(47)

3 鋼骨-組合L形鋼管混凝土中長柱軸壓承載力計算

3.1 中長柱穩定系數計算公式

根據中國相關規程，包括GB 50936—2014、CECS28:2012、DL/T—5085—1999中對于中長柱承載力的計算，普遍采用短柱軸壓承載力乘以穩定系數。本文采用式(47)所得到的短柱承載力計算結果再乘以穩定系數，確定長柱承載力，計算式為

NL=φNu

(48)

(49)

相對長細比公式為

(50)

式中：Nu為短柱承載力，按照式(47)計算；L0為柱的計算長度；Et、Es、Ec分別為鋼管、鋼骨、混凝土的彈性模量；It、Is、Ic分別為鋼管、鋼骨、混凝土的截面最小形心慣性矩，計算公式由3.2節給出；γ為混凝土剛度折減系數，EcIc所占比重較小，故取γ=1。

3.2 L形鋼骨-鋼管混凝土柱最小形心主慣性矩的確定

組合異形柱形心的確定對于軸壓承載力的研究有重要的意義，L形鋼骨-鋼管混凝土柱由鋼管、混凝土以及鋼骨組成，三部分的材料不同，從而剛度以及彈性模量不同，故其形心不能按照外形確定。本文按照剛度換算截面法來確定形心，將混凝土的面積按照等剛度原則換算成鋼材的面積，然后分別和矩形和方形兩部分的鋼管面積、鋼骨面積相加，組成形心不變、剛度相等的兩部分面積A1和A2，建立坐標如圖3，利用形心公式計算L形鋼骨-鋼管混凝土柱的形心。

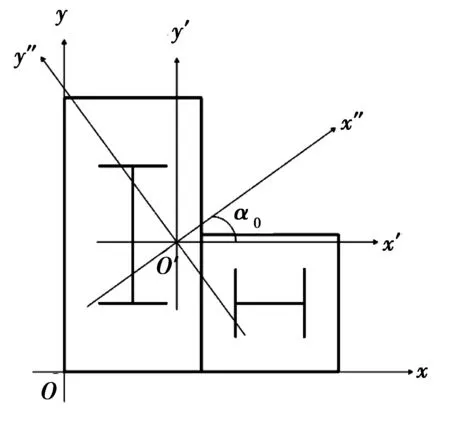
圖3 L形組合柱形心Fig.3 L-shaped Composite column

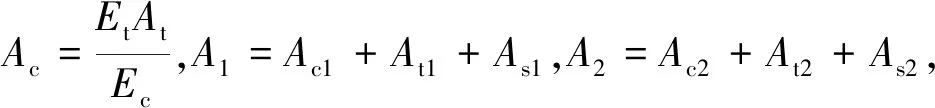
(51)

(52)

從而確定形心位置O′點，以O′為中心點建立X′-Y′坐標系，分別計算鋼管、混凝土、鋼骨的形心慣性矩，即Ixt、Ixc、Ixs、Iyt、Iyc、Iys、Ixyc、Ixyt、Ixys，可得形心慣性矩及慣性積為

Ix′=Ixc+Ixt+Ixs

(53)

Iy′=Iyc+Iyt+Iys

(54)

Ix′y′=Ixyc+Ixyt+Ixys

(55)

故可求得形心主慣性軸轉動角度的正切值

(56)

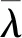
(57)

(58)

式中：Ix1、Iy1為主慣性矩。

4 理論公式驗證及參數分析

4.1 理論公式驗證

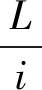
表1 L形短柱承載力計算與試驗值比較Table 1 Comparisons of L-shaped short column between calculation results and experiment results of bearing capacities

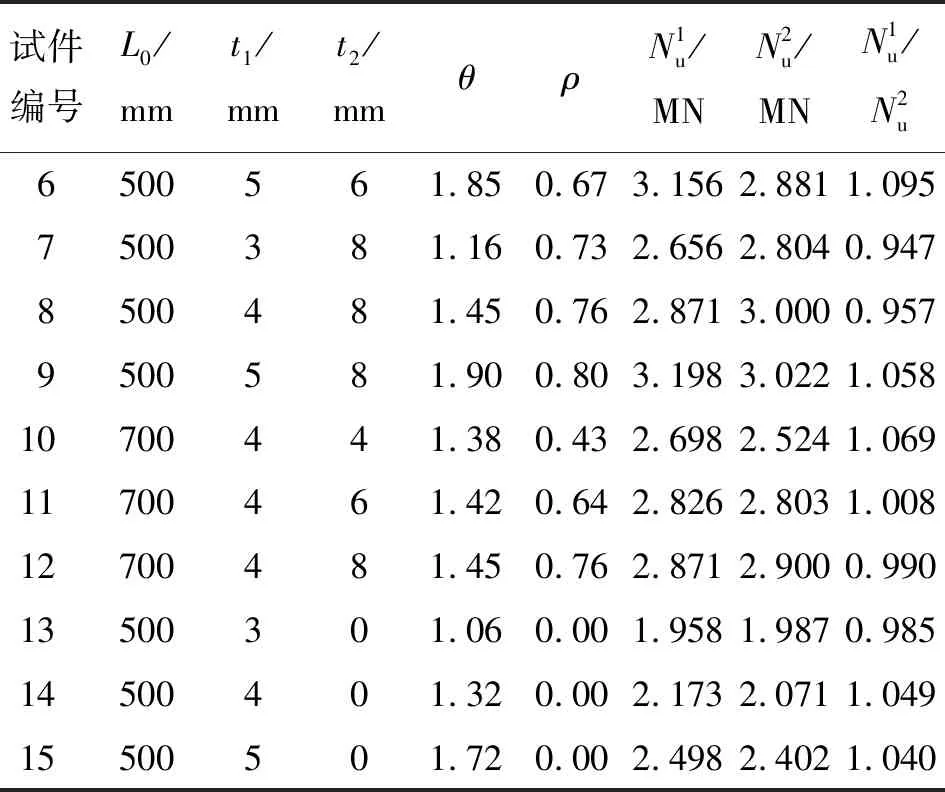
續表1

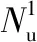
表2 L形中長柱承載力計算與試驗值比較Table 2 Comparisons of L-shaped long column between calculation results and experiment results of bearing capacities

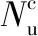
4.2 影響因素分析

4.2.1 混凝土k的影響 對于鋼管混凝土，k=1.5～3.0，考慮鋼骨對于混凝土套箍作用的提高，取k=3.0。取短柱3號試件(見表1)，其他參數不變，系數k在1.5～3.0變化時，由圖4可知，隨著k的增長，短柱軸壓承載力隨之呈線性增長，但k值也不可能無限增大，它與材料的軸壓性能有關。k的增大表明混凝土內摩擦角增大，抗拉強度增強。

對于內置鋼骨的鋼管混凝土而言，由于鋼骨的存在，一方面有效延緩了混凝土斜裂縫的產生，使核心混凝土的抗剪切能力提高；另一方面，外包鋼管對核心混凝土的套箍作用得以提高，相應地增大了混凝土內摩擦角，使得該類異形組合柱承載力提高。在k=3.0時，所得承載力與試驗數據吻合較好。

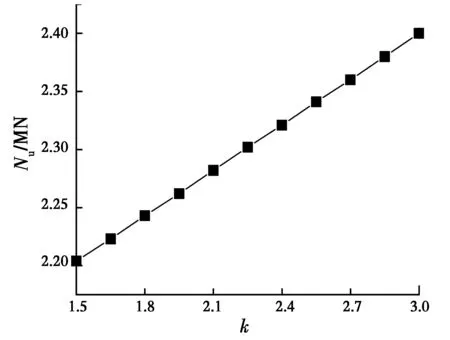
圖4 k對承載力的影響Fig.4 Effect of k on the bearing

4.2.2 鋼骨材料拉壓比α的影響 組合短柱軸壓承載力受鋼骨影響較大，而鋼骨的承載力主要與拉壓比α、含骨率ρ有關。但對于高強鋼材，考慮鋼材的SD效應，材料拉壓比不再等于1，對于韌性金屬材料，α一般為0.77～1.00[21-22](如AISI 4330，α≈0.87; AISI 4320，α≈0.92; AISI 4310，α≈0.95[23])。圖5為基于式(47)得到的鋼骨-組合L形鋼管混凝土短柱軸壓承載力隨材料拉壓比α和含骨率ρ的變化曲線。由圖5可知，隨著拉壓比α的增加，軸壓承載力不斷降低；當保持α不變，隨著含骨率ρ的不斷增加，L形組合結構承載力不斷增大。

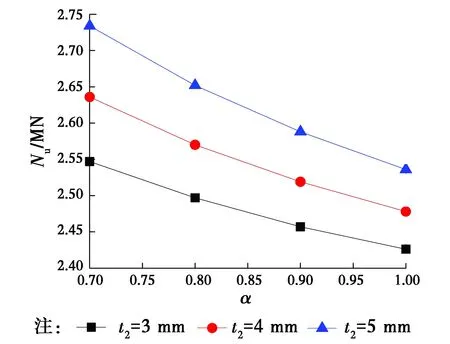
圖5 拉壓比α、含骨率與承載力Nu的關系Fig.5 Ralationship of bearing capacity and pull pressure ratio α、osseous rate

由圖5可以看出，拉壓比α對短柱承載力的影響相對較小。當拉壓比取值相差超過0.3時，對于承載力的影響接近3%，故在計算鋼骨承載力時，可忽略拉壓比的影響，但對于材料拉壓比α較小時，考慮其影響能夠取得更加精確的承載力計算值。鋼骨含骨率對短柱承載力影響較大，當其他參數不變，鋼骨厚度增加1 mm，對承載力的影響超過5%。

5 結論

1)基于統一強度理論，對鋼骨-組合L形鋼管混凝土短柱以及中長柱軸壓受力性能進行了理論研究，分別建立了其軸壓承載力計算公式，并與試驗數據進行對比驗證，吻合較好，從而驗證了本文研究方法的正確性，為內置鋼骨的組合異形鋼管混凝土柱軸壓承載力計算提供了參考。

2)隨著k值的增大，即混凝土內摩擦角不斷增大，短柱軸壓承載力增大，而鋼骨的存在能夠有效提高對混凝土的套箍作用，提高混凝土的內摩擦角，從而取得較高的承載力。

3)材料拉壓比α對短柱承載力具有一定影響，隨著材料拉壓比α的增大，承載力不斷降低，對于拉壓比較小的鋼材，考慮拉壓比能夠取得更加精確的承載力計算值；含骨率ρ對短柱承載力有較大的影響，隨著含骨率ρ的增加，短柱承載力逐漸增大。

4)所得計算式能充分考慮鋼骨拉壓比的不同，具有廣泛應用性；合理考慮鋼骨組合L形鋼管混凝土柱的劃分方法、承載力影響因素以及應用統一強度理論，為工程應用提供了相應的理論依據。