基于累積殘差貢獻率的傳感器故障定位方法

安星，劉綱，張亮亮，李立力

(重慶大學 土木工程學院；山地城鎮建設與新技術教育部重點實驗室，重慶 400045)

結構健康監測旨在通過監測結構行為及時識別結構損傷，實時評估結構性能，已成為土木工程領域的重要研究方向[1]。如今，越來越多的橋梁都安裝了結構健康監測系統，其中，傳感器是健康監測系統最前端的設備，用于獲取結構響應及采集各種監測信息，其精度和性能的好壞將直接影響最終的評估結果[2]。然而，相較于橋梁上百年的使用壽命而言，傳感器的使用壽命僅為十幾年甚至幾年。傳感器在使用過程中會因為老化或外界因素影響而出現故障，這會使結構安全狀態評估出現漏報或誤報，造成不必要的經濟損失。

近年來，傳感器故障問題已逐步引起業界專家的重視，并開展了初步的理論研究。在傳感器故障的統計分類方面，何富君等[3]總結了傳感器的4類典型故障：卡死、恒增益、固定偏差和線性偏差。Yi等[4]對其進行了拓展，將傳感器的故障類型劃分為7類：固定偏差、線性偏差、恒增益、精度下降、卡死、白噪聲卡死、零線漂移。在橋梁結構健康監測領域，如何實現傳感器故障診斷的研究報道不多，但在控制工程領域，大量學者和工程界人士開展了深入研究，取得了豐碩成果。已有的傳感器故障診斷方法可大致分為3類[5]：基于解析模型、基于信號處理和基于知識經驗的方法。目前應用最廣泛的是基于信號處理的方法，其中主元分析(Principal Component Analysis，PCA)是一種基于信號處理的多元統計分析方法，在多變量高斯分布數據集建模方面具有出色的性能，已廣泛應用于控制工程與故障診斷領域[6-8]。一些學者對PCA方法進行了改進[9-10]，提高了PCA對故障的識別率，擴展了PCA方法的適用范圍。已有學者嘗試用PCA識別土木工程結構健康監測系統中傳感器的故障，Hernandez-Garcia等[10]、胡順仁等[11]將PCA方法應用于實際橋梁結構的傳感器故障監測；Huang等[12]、Rao等[13]根據實驗室模型獲得的數據，采用PCA方法研究了傳感器故障定位。

基于PCA原理，在傳感器故障定位方面應用較多的是貢獻圖定位法[10-11]，但傳統貢獻圖定位法僅對故障期間某一時刻的數據進行分析，容易出現誤判。其次，基于PCA的缺失變量法[12-13]雖能準確識別故障傳感器，但針對監測系統中的每個傳感器需循環計算，過程比較繁瑣。另外，符號有向圖法[14-15]能較好應用于各傳感器之間有因果關系的監測系統，例如，化工、冶金工程等的傳感器故障定位，但橋梁結構中各傳感器的故障往往相互獨立，因此，限制了該方法在橋梁結構健康監測系統中的應用。

綜上所述，在土木工程領域，現有研究大多只分析一類或兩類傳感器故障，且只對單個傳感器故障進行識別和定位，對兩個或多個傳感器同時發生故障的情況研究較少。同時，在橋梁結構健康監測系統中加速度傳感器故障診斷的研究成果也較少。筆者通過改進現有的殘差貢獻圖，提出累積殘差貢獻率指標，從而提高傳感器故障定位的準確率，且可實現兩個傳感器同時發生故障時的定位，然后通過三跨連續梁數值算例驗證方法的適用性。

1 PCA基本原理及故障檢測

1.1 基本原理

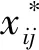
(1)

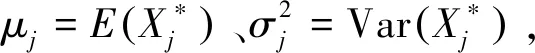
將處理后的m個傳感器數據按列向量排列，組成n×m維的矩陣X，并計算X的協方差矩陣S。

(2)

S是一個m×m的矩陣，求出矩陣S的特征值λi和對應的特征向量Pi，并將特征值按從大到小排列，即λ1≥λ2≥…≥λm≥0。其中，Pi為第i主軸，其每個元素的值分別對應第i主軸與每條原坐標軸的夾角余弦值；λi表示矩陣X變換到Pi主軸后的方差。

令XPi=ti，ti為X在第i主軸的投影，表示第i主成分，也叫第i主元。矩陣X可表示為

(3)

通常采用特征值累積和百分比法確定所需的主元個數，較多文獻建議取累積和達到85%[16]時確定主元個數k。

(4)

這樣即能反應原始數據信息，又能達到降維的目的。確定主元個數k后，式(3)可寫成

(5)

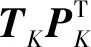
從以上過程可知，主元分析是一個降維的過程，降維的方法是通過基坐標向量的平移和旋轉，把一個高維的信息投影到低維子空間，并保留主要信息。

1.2 故障檢測

PCA的故障檢測依賴于各傳感器的相關性，若某一測點傳感器發生故障，將會使之前建立起來的相關關系發生改變，造成統計指標數據異常。

PCA故障檢測有兩個統計指標，即HotellingT2統計量和SPE統計量。

在第i個時間點下，過程變量標準化數據為Xi，HotellingT2統計量定義為

(6)

式中：λ為主元特征值構成的對角矩陣；PK=[P1,P2,…,Pk]，為主元特征向量構成的矩陣。

T2表示馬氏距離，為Xi在主成分空間的投影點到主成分空間重心的距離。T2統計量的分布近似服從F分布，其控限可通過式(7)計算。

(7)

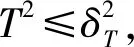
SPE統計量稱為殘差統計量，也叫Q統計量，定義為

(8)

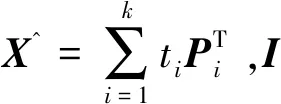
SPE表示歐氏距離，當檢驗水平為α時，可按式(9)確定其控限值Qα。

(9)

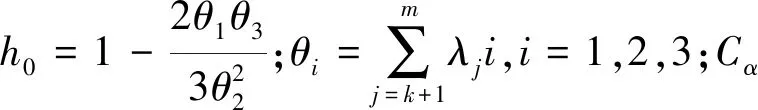
如果Q≤Qα，則傳感器正常；如果Q>Qα，則傳感器出現了故障。

2 累積殘差貢獻率法

已有研究[10]表明，SPE統計量對傳感器故障更為敏感，在貢獻圖的基礎上，提出累積殘差貢獻率指標。

2.1 殘差貢獻圖

殘差貢獻圖即采用某一時刻傳感器數據的殘差貢獻值作圖，其計算式為

(10)

式中：ei,j為第i時刻下第j傳感器數據的殘差，j=1,2，…，m。在殘差貢獻圖中，可按照高貢獻值的傳感器即為故障傳感器的原則[17]定位出故障傳感器。

應該指出的是，貢獻圖有時不能準確定位故障傳感器，主要是因為貢獻圖僅取故障產生的某一個時刻進行殘差貢獻值分析，但由于環境、外界激勵的隨機性，故障傳感器會受到與之相關性較強的傳感器的干擾，存在某些時刻正常傳感器貢獻值大于故障傳感器的情況，容易得到錯誤的結果。文獻[10]也指出，在某一時刻，正常傳感器與故障傳感器關聯性可能較大，會對故障的定位造成干擾。因此，并非每個時刻故障傳感器的貢獻值都是最高，尤其是在多個傳感器同時發生故障時，貢獻圖容易得出錯誤的結果，產生誤判。

2.2 累積殘差貢獻率

雖然某個時刻故障傳感器的殘差貢獻值不一定較大，但從統計意義上講，其殘差貢獻值在一段時間內應總體偏大，故在傳統貢獻圖的基礎上提出了累積殘差貢獻率法。

首先，定義第i時刻j傳感器數據的殘差貢獻率為

(11)

殘差貢獻率具有以下性質：

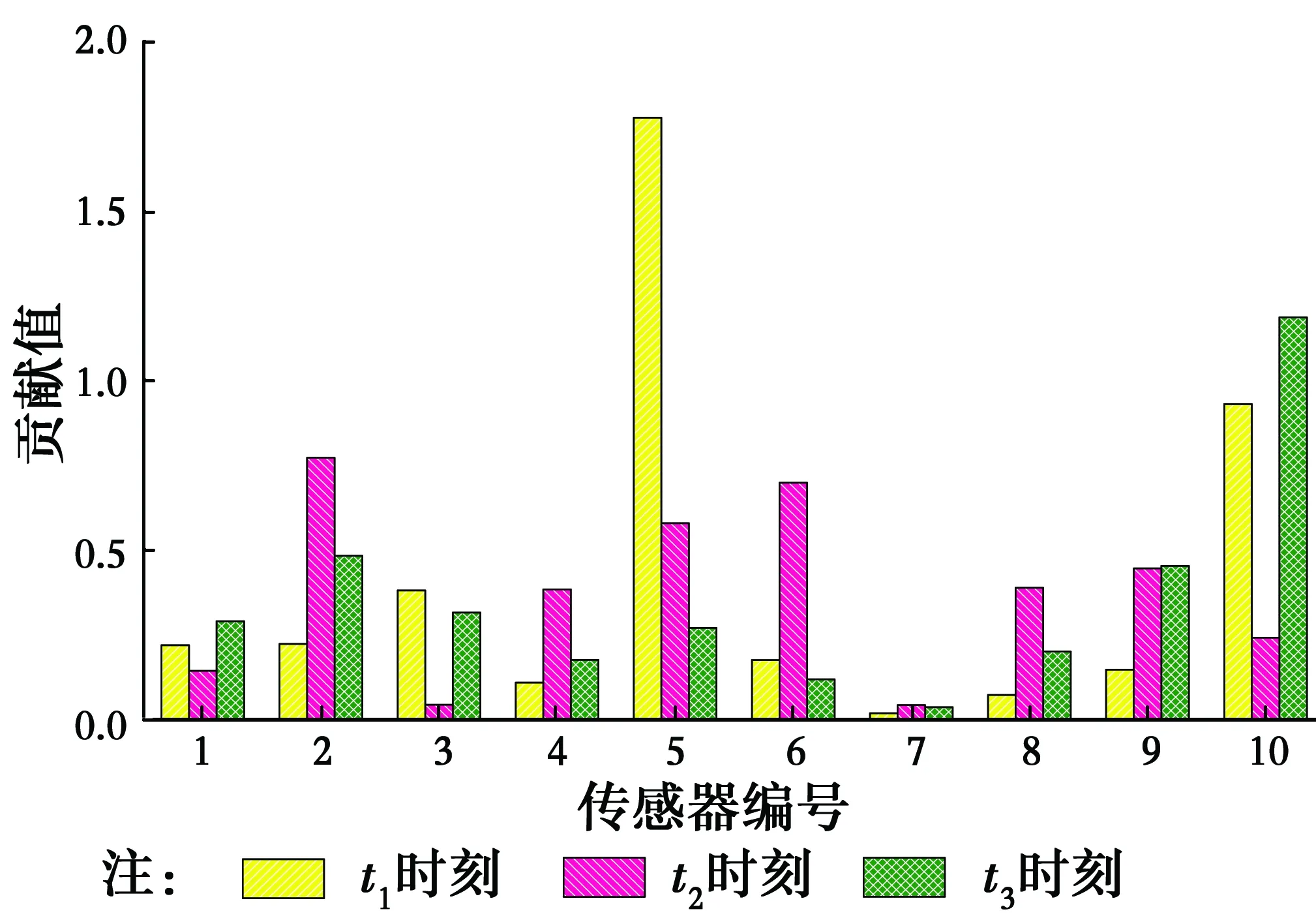
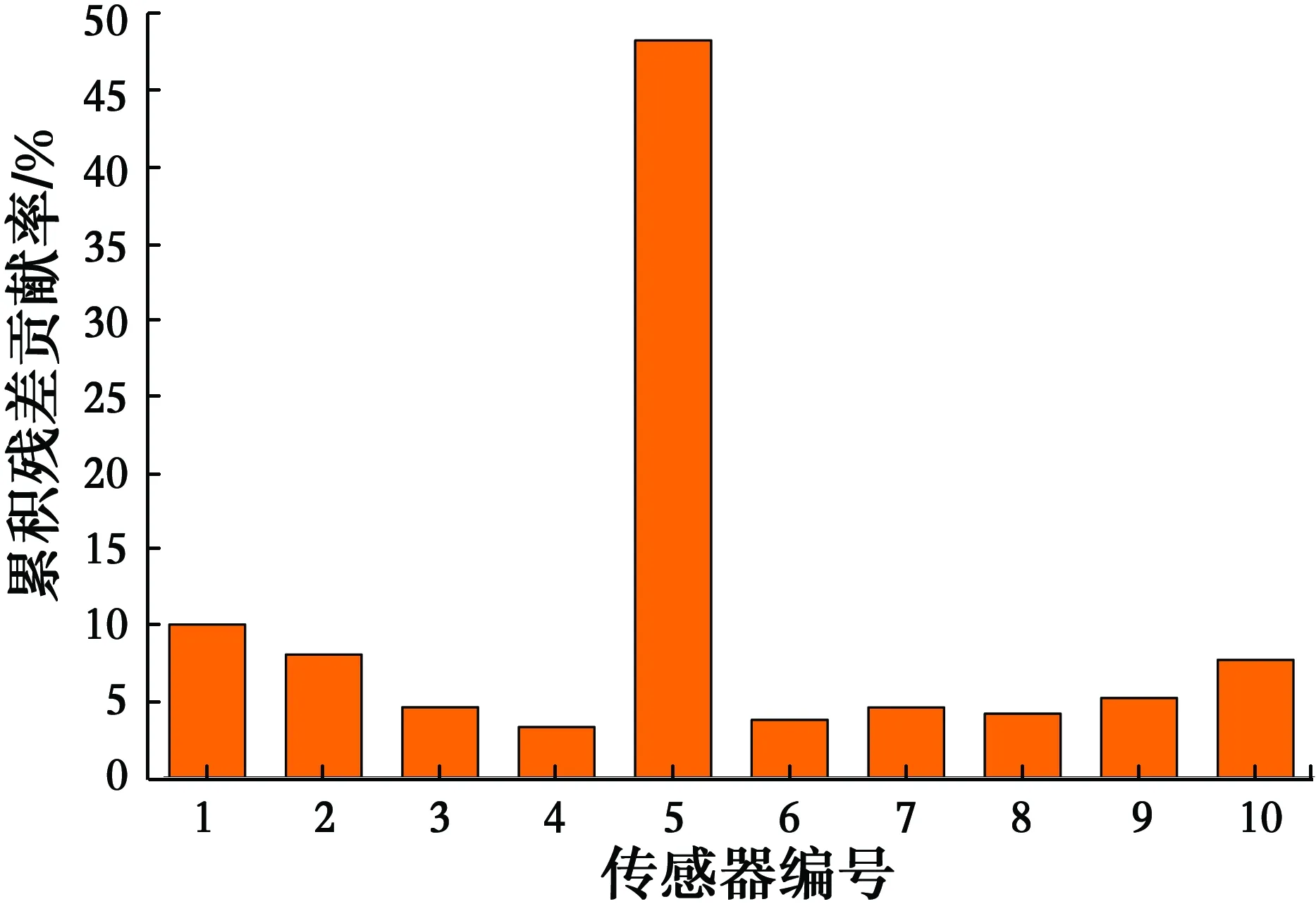
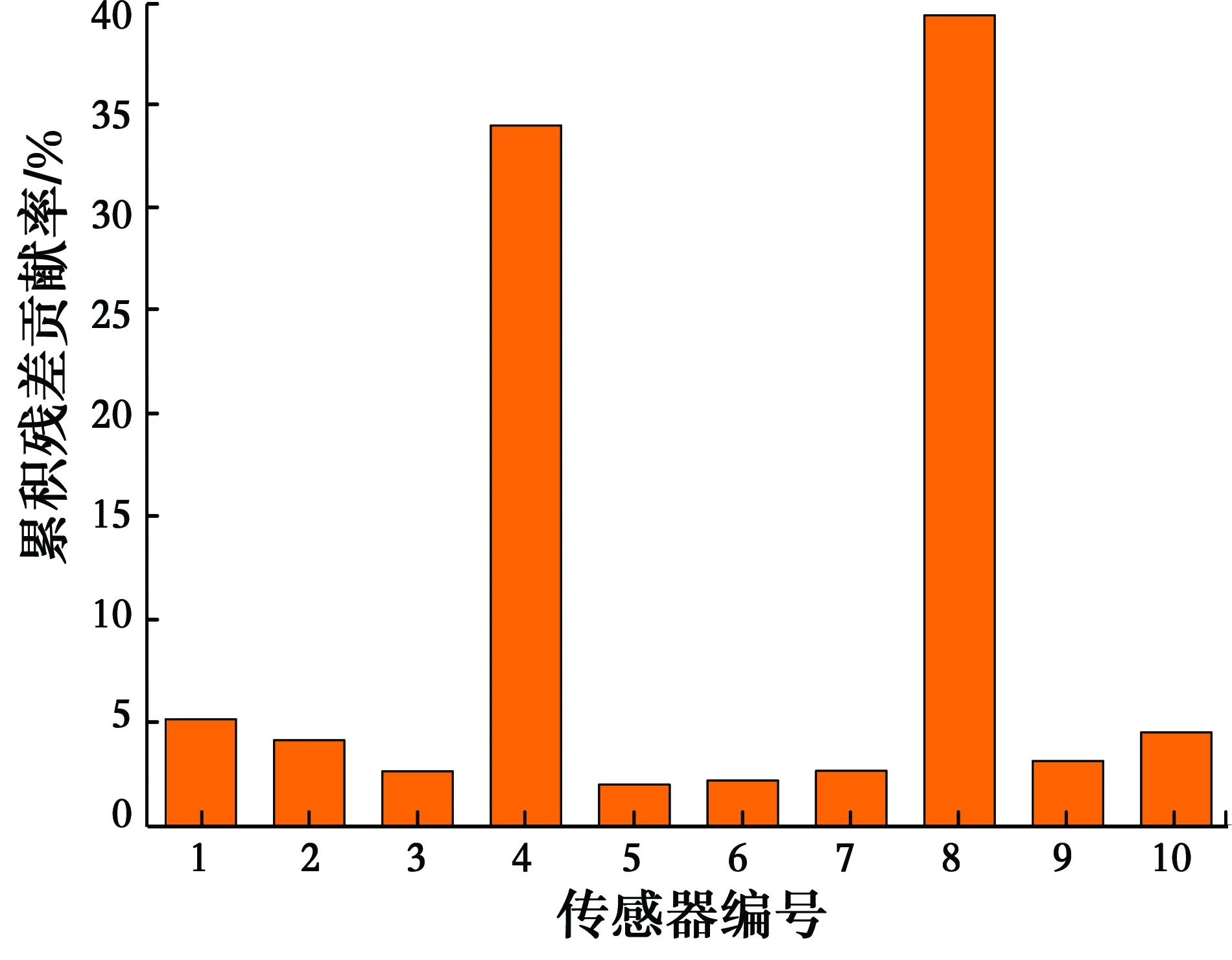
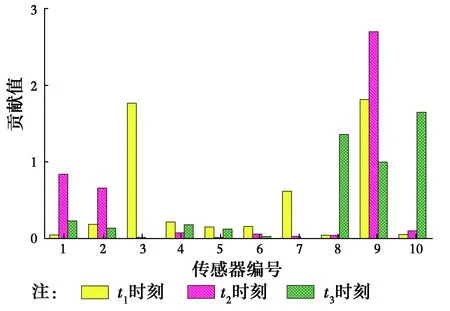
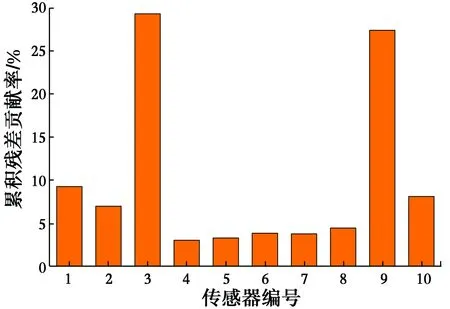
1)0

其次，分別計算故障時間段內N組數據的殘差貢獻率，并按式(12)進行加權，得到第j個傳感器的累積殘差貢獻率。

(12)

最后，將各傳感器的累積殘差貢獻率作圖，按照累積殘差貢獻率指標明顯偏大即為故障傳感器的原則進行傳感器故障定位。

累積殘差貢獻率圖是對傳統殘差貢獻圖的改進，其保留了SPE統計量對傳感器故障較為敏感的特性。相對于殘差貢獻圖，累積殘差貢獻率圖引入了統計概念，通過較長時間段內殘差貢獻值的加權平均來弱化某個時刻殘差貢獻值有偏差的情況，從而提高故障傳感器定位精度。同時，累積殘差貢獻率將殘差貢獻值歸一化到[0,1]之間，更有利于直觀定位故障傳感器。

3 傳感器故障模型

傳感器在正常工作過程中，不可避免地會受到噪聲的干擾，所以，傳感器返回來的數據與真實值有一定的偏差。用y*(t)表示t時刻被測變量的真實值，w(t)表示傳感器測量噪聲[4]，則由傳感器顯示的正常值y(t)可以表示為

y(t)=y*(t)+w(t)

(13)

當傳感器的測量值與測量變量的真實值存在無法接受的偏差時，傳感器被認為是有故障的。在傳感器的7類故障中，白噪聲卡死故障與零線漂移是卡死故障的特殊情況，精度下降是偏差故障的特殊情況。為節省篇幅，僅討論更為廣泛的4類故障。表1中列出了4種典型傳感器故障的數學表達式，其中，a、b、c、f和G是描述相應傳感器故障幅度的5個參數。

表1 4類典型的傳感器故障數學表達式Table 1 Mathematical expressions of four typical sensor fault types

4 數值模擬分析

采用ANSYS軟件建立三跨連續梁模型，模型的彈性模量E=3×1010N/m2，泊松比μ=0.3，密度ρ=2 500 kg/m3，模型尺寸為梁長40 m，截面為0.25 m×0.6 m的矩形。將三跨連續梁均分為200個單元，每個單元長度為0.2 m。采用白噪聲地脈動作為連續梁的激勵，使用Newmark-β法計算連續梁的加速度時程響應[18]。假設加速度傳感器布設在距離左端支座3、6、9、15、18、21、25、33、35、38 m處，共計10個傳感器，依次編號為1～10，如圖1所示。

圖1 三跨連續梁模型Fig.1 A Three-span continuous beam

試驗過程中假設結構完好，僅傳感器發生故障。首先生成115條均值為0、方差為1的隨機白噪聲作為地脈動激勵，施加于結構。其中前100條結構響應數據用于PCA訓練；第101至105條用于檢驗單個傳感器發生恒增益故障的情況，記為工況1；第106至110條用于檢驗恒增益故障和固定偏差故障同時發生的情況，記為工況2；第111至115條用于檢驗卡死故障和固定偏差故障同時發生的情況，記為工況3，如表2所示。

根據參考文獻[12，19]的建議，設置3種工況中各類傳感器故障的幅度，如表2所示。

表2 3種傳感器故障工況Table 2 Three kinds of sensor failure conditions

注：斜率f9滿足在故障時間段內偏差故障從0線性增加到σ9。

假設三跨連續梁加速度傳感器對每條地脈動波都采集100個數據，則每個樣本的樣本容量為100。傳感器處于正常狀態時共有100個訓練樣本，用于PCA訓練，上述3種故障工況下各有5個不同的測試樣本，這些采集到的樣本數據均是真實值。

為模擬實際監測系統的環境干擾，在ANSYS計算的結構響應數據中加入噪聲。根據Hernandez-Garcia等[10]、Huang等[12，19]的研究，實際監測系統中傳感器的信噪比大致在15～25 dB之間，設置信噪比為20 dB，即噪聲信號的均方根為真實信號均方根的10%。同時，為了更為真實地模擬現實環境中的有色噪聲，首先產生10%均方根的白噪聲，然后對白噪聲進行有色處理，但為了避免數據失真，將有色噪聲控制在均值為0，均方差為0.1σ的范圍內。有色噪聲的類型復雜，公式繁多，采用較為常見的有色噪聲公式，令

Cn(t)=Wn(t)+0.5Wn(t-1)

(14)

式中：Cn(t)為t時刻的有色噪聲；Wn(t)為t時刻10%均方根的白噪聲。按照式(4)在數值模擬得到的加速度中加入有色噪聲，以此模擬傳感器顯示的正常數值，再進行PCA訓練。傳感器故障的輸出信號按表1中的模型進行模擬。

4.1 單傳感器故障定位

在工況1下，經PCA檢驗后，其T2統計量與SPE統計量結果如圖2所示，其中虛直線為各統計量置信度α=99%的閾值。從統計量的結果發現，雖然T2統計量沒有超限，但SPE統計量存在大量超限的點，超限率為15.56%，達到了規定限值，可以判斷該過程中存在故障。

T2統計量檢測的是主元空間的數據變動，SPE統計量檢測的是殘差空間的數據變動。從圖2可知，在傳感器故障檢測中，T2統計量不如SPE統計量敏感，對傳感器故障數據的識別較差。所以，在下文的故障識別與定位過程中，僅討論SPE統計量及其改進的累積殘差貢獻率。

隨機選取3個時刻，記為t1、t2和t3，作這3個時刻的殘差貢獻值圖，如圖3所示。從該圖可知，t1時刻5號傳感器的貢獻值最高，可以正確定位出5號傳感器為故障傳感器，但在t2和t3時刻并不是5號傳感器的貢獻值最高，出現了誤判現象。

圖2 工況1下PCA檢驗統計量Fig.2 PCA test statistics result of condition

圖3 工況1某一時刻殘差貢獻值Fig.3 residual contribution value of condition

采用該方法，作累積殘差貢獻率圖如圖4所示。該圖顯示5號傳感器的累積殘差貢獻率最高，故可以正確定位故障傳感器。

圖4 工況1累積殘差貢獻率Fig.4 Accumulated residual contribution rate of condition

為討論累積次數N對故障定位的影響，計算不同N下累積殘差貢獻率如圖5所示，圖中1～10表示傳感器的編號。由該圖可知，累積超過50個時間步之后，故障傳感器的累積殘差貢獻率開始突出，其他傳感器的貢獻率開始弱化。累積次數超過100次后，各傳感器的累積殘差貢獻率趨于穩定。因此，為了準確定位故障傳感器且減少計算時間，建議累積次數N取值為100。

圖5 不同累積次數對故障定位的影響Fig.5 The relationship between cumulative residual contribution rate and cumulative

4.2 兩傳感器故障定位

在工況2下，SPE統計量的超限率為31.11%， 隨機選擇3個時刻，分別命名為t1、t2、t3，作這3個時刻的殘差貢獻值圖如圖6所示。從圖6可知，t1時刻4號和8號傳感器的貢獻值遠大于其他傳感器，可以定位出這兩個傳感器發生故障；但t2時刻8號傳感器和10號傳感器的貢獻值較大，出現了錯判；t3時刻僅能判斷出4號傳感器發生了故障。因此，傳統的貢獻圖法在多傳感器同時發生故障時更容易出現誤判。

采用累積殘差貢獻率作圖如圖7所示，4號傳感器和8號傳感器的累積殘差貢獻率遠大于其他傳感器的累積殘差貢獻率，可以判斷這兩個傳感器發生了故障。

圖6 工況2某一時刻殘差貢獻值Fig.6 residual contribution value of condition

圖7 工況2累積殘差貢獻率Fig.7 Accumulated residual contribution rate of condition

在工況3下，經PCA檢驗后，其SPE統計量的超限率為13.3%，故可判斷有傳感器故障發生。隨機選取3個時刻作殘差貢獻值圖如圖8所示，累積殘差貢獻率圖如圖9所示。圖8和圖9表明，傳統的殘差貢獻值法定位存在誤判情況，而累積殘差貢獻率能夠準確定位出發生故障的傳感器。

圖8 工況3某一時刻殘差貢獻值Fig.8 residual contribution value of condition

圖9 工況3累積殘差貢獻率Fig.9 Accumulated residual contribution rate of condition

5 結論

針對實際結構健康監測系統中傳感器可能發生故障而影響后期結構安全評估的問題，在傳統殘差貢獻圖法的基礎上，基于統計原理提出了累積殘差貢獻率法，數值模擬算例表明：

1)主元分析的SPE統計量能識別出傳感器故障，說明在傳感器故障識別中SPE統計量比T2統計量更為敏感，這與已有文獻的結論一致。

2)累積殘差貢獻率將殘差貢獻值歸一化到[0,1]之間，更有利于直觀定位故障傳感器。無論是單傳感器損壞還是兩個傳感器損壞，該方法較傳統貢獻圖法能更準確地定位故障傳感器。

3)累積殘差貢獻率通過對故障時間段的殘差貢獻率進行加權平均，提高了故障定位的精度。累積的故障時間越長，故障定位越準確，為了準確定位故障傳感器且減少計算時間，建議累積次數N取值為100。

應該說明的是，筆者在驗證所提方法的過程中，假設結構完好，僅傳感器發生故障。這主要是因為實際工程結構的損傷通常是累積損傷，需多月或多年才有明顯的變化，而傳感器發生故障的時間尺度遠小于結構損傷的時間跨度。但如何分離傳感器自身故障和結構損傷仍需今后進一步研究。