越肩發射反導攔截彈復合制導律研究

任 越，楊 軍

(西北工業大學航天學院，西安 710072)

0 引言

現代作戰飛機的自衛攔截手段可分為被動防御和主動防御兩類。被動防御手段包括隱身技術、誘餌技術及誘騙技術等，完全是一種消極被動的逃避方式。隨著導彈技術的不斷完善，這種消極被動的逃避方式幾乎不能確保飛機的有效生存，科索沃戰爭中，造價數億美元的F-117隱身戰斗機，被廉價的SA-3導彈所擊毀，就是最好的例證。主動防御技術則采用機載反導攔截武器主動摧毀來襲導彈，能夠更好地提高飛機生存能力。機載反導攔截武器主要包括機載定向能武器(主要是激光)和機載反導攔截彈兩類[1]。本文研究的對象即為機載反導攔截彈。

考慮不同載機平臺面臨的主要威脅，反導攔截彈應具備攔截中遠距空空彈的能力。同時，反導攔截彈應能夠幫助載機瓦解來襲導彈尾追、側擊和迎擊這三種典型攻擊態勢，實現全向攻擊。其中攔截尾追目標需要采用越肩發射來實現對尾后目標的攻擊，也是攔截技術的難點。

越肩發射導彈的制導過程一般由發射后的轉彎段和末制導攻擊段組成。轉彎段的目的是使導彈快速轉向目標，當滿足中末制導交班條件時進入末制導。從查閱情況來看，轉彎段導引律一般以快速性或者速度為指標進行設計，文獻[2]使平行于初始視線方向上的速度分量最大，并以終端速度最大為指標，根據極小值原理設計了轉彎段制導律。反導攔截需要實現對來襲彈的直接碰撞，對脫靶量要求極高，同時來襲彈為具備高速、高機動能力的戰術空空彈，因此對末制導律要求較高。針對高速、高機動目標的末制導律，一般以各種形式的最優制導律和變結構制導律為主，文獻[3]考慮了能量管理和優化問題，以零控脫靶量和交會角為指標設計了最優制導律。

借鑒相關文獻的研究成果，本文以攻角作為控制量，采用偽譜法設計了反導攔截彈的轉彎段制導律，并采用變結構控制理論設計了末制導律。同時建立了載機攜帶攔截彈對來襲空空彈的反導對抗模型，利用設計的攔截彈復合制導規律對尾追目標實現了攔截仿真。

1 轉彎段制導律設計

采用質點運動方程對轉彎段軌跡進行優化，并給出最優攻角指令，為了簡化設計，提出以下假設：

1)不計操縱力、旋轉力和非定常氣動力；

2)攔截彈采用側滑控制技術(Side to Turn，STT)轉彎，滾轉通道穩定，滾轉角恒定。

設狀態變量x=[V,θ,ψV,h]T,控制變量u=[α,β]T，彈道坐標系下的導彈三自由度方程為

(1)

式中，m為質量，V為速度，θ為彈道傾角，ψV為彈道偏角，h為高度，α為攻角，β為側滑角；Q為動壓，S為參考面積，CD為阻力系數，CY為升力系數，CZ為側力系數；P為主發動機推力；g為重力加速度。

本文用Radau偽譜法求解最優轉彎規律。Radau偽譜法的配點為Legendre-Gauss-Radau(LGR)點，該方法以較少的節點獲得很高的求解精度，精度僅次于Gauss偽譜法，但收斂速度更快[5]。GPOPS-II軟件是一個較為成熟的用Radau偽譜法求解最優控制的軟件，求解時需要輸入微分方程、邊界條件、邊界約束、狀態約束、性能指標以及容許控制等。

考慮攔截彈轉彎段邊界條件，轉彎段速度不能太大，以減小需用過載，初速則和載機相同。轉彎結束后攔截彈的速度矢量應大致指向來襲彈。優化的邊界條件為

(2)

邊界約束為

(3)

采用大攻角轉彎可以減小轉彎時間，但是攻角過大，氣動特性會異常復雜，所以攔截彈的轉彎應在合適的攻角范圍內進行。本文將攔截彈的攻角限制在40°，狀態約束設為

(4)

攔截彈應在盡量短的時間內完成轉彎，所以將轉彎時間最短作為性能指標

(5)

利用Radau偽譜法完成對連續最優控制問題的離散化后,采用snopt求解器對離散最優控制進行求解，得到優化的狀態信息和控制信息。對優化后的攻角曲線進行擬合以給出攻角指令。

擬合后的攻角指令以下面形式給出

αc=a6t6+a5t5+a4t4+a3t3+a2t2+a1t+a0

(6)

邊界條件中不同的θf會優化出不同的攻角指令，以θf為自變量對αc中的系數a0～a6進行線性擬合，表達式如下

a6=b61θf+b60,a5=b51θf+b50a4=b41θf+b40,a3=b31θf+b30a2=b21θf+b20,a3=b11θf+b10a0=b01θf+b00

各項系數具體數值如下

b61=0.0049,b60=-0.7876b51=-0.0386,b50=6.2092b41=0.1110,b40=-18.0444b31=-0.1443,b30=23.7847b21=0.0885,b20=-14.7768b11=-0.0244,b10=4.0897b01=0.0025,b00=0.2939

法向過載的計算公式為

nyc=[Psinαc+QSCY(αc)]/mg

(7)

將攻角指令代入式(7)，得到轉彎段過載指令

nyc=[Psin(a6t6+a5t5+a4t4+a3t3+a2t2+

a1t+a0)+QSCY(a6t6+a5t5+a4t4+

a3t3+a2t2+a1t+a0)]/mg

(8)

2 末制導律設計

2.1 數學模型的建立

攔截彈為STT轉彎，假設保持滾轉軸穩定，則導彈的控制可以解耦在2個相互正交的通道內。本文對末制導律的設計在縱向平面內開展，并假設攔截彈與目標的相對運動方程可在初始目標視線附近線性化。攔截彈與目標的相對運動關系如圖1所示。

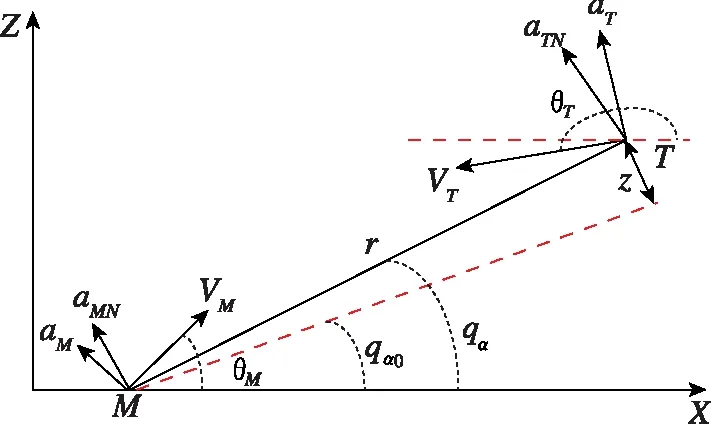
圖1 縱向平面內彈目相對運動關系幾何Fig.1 Relative kinematics relationship betweenmissile and target in longitudinal plane

圖1中，下標M和T分別代表攔截彈和目標的相應變量。V、a、θv分別代表速度、側向加速度和彈道傾角。qα代表視線高低角，r表示彈目相對距離。z表示某一時刻彈目視線與初始視線在法線方向的相對位移。

根據圖1可以得到

(9)

彈目在視線切線方向上的相對速度為

Vq=-VMsin(θM-qα)+VTsin(θT+qα)

(10)

彈目在視線法線方向上的相對速度為

Vq=-VMsin(θM-qα)+VTsin(θT+qα)

(11)

Vq同時可以表示為

(12)

假設目標的機動為一階動力學，則

(13)

式中，τT為目標的一階時間常數。

假設攔截彈的機動為一階動力學，則有

(14)

式中，τM為導彈的一階時間常數。

(15)

2.2 零控脫靶量

變結構制導律的滑膜面常選用視線角速度，但是制導末端彈目關系變化劇烈，導致視線角速度驟變、控制信號惡劣。針對具有高速、大機動能力的來襲目標，本文選取零控脫靶量(Zero Effort Miss，ZEM)作為滑膜面。零控脫靶量的含義是從當前時刻開始，目標保持當前機動不變，導彈控制量為0的最終脫靶量。

由零控脫靶量的定義可以將式(15)轉化為齊次方程

(16)

x=[x1x2x3x4]T

(17)

對齊次方程進行Laplace變換，可以得到：

x4(s)=x40/(s+1/τM)

(18)

x3(s)=x30/(s+1/τT)

(19)

(20)

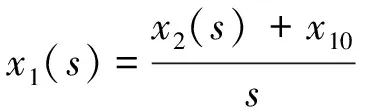
(21)

對x1(s)進行Laplace逆變換得

(22)

任意時刻的ZEM可以表示為

(23)

其中：ψ(tgo/τ)=e-tgo/τ-1+tgo/τ。

根據幾何關系可以得到

z=-Vrtgoqα

(24)

(25)

ZEM可以寫為

(26)

2.3 變結構制導律設計

考慮簡化的導彈、目標動力學一階環節與實際動力學之間的有界誤差分別為ΔaMN、ΔaTN，同時目標加速度為有界未知變量

(27)

(28)

利用相對運動方程

(29)

(30)

對s進行微分運算：

(31)

結合相對運動方程和式(31)可以得到

(32)

(33)

根據Lyapunov第二法選取Lyapunov函數為

L=s2/2

(34)

(35)

將控制量代入V中，得到

(36)

(37)

因為η大于系統總擾動的界Δ，所以V<0，系統穩定。

為了削弱滑膜控制的抖振，采用連續高增益法，用連續函數w(s)取代sgn(s)

(38)

式中，δ是很小的正常數。

因此，末制導段縱向平面法向過載指令為

(39)

側向平面采用次最優導引律為

(40)

式中，導航比N=4。

3 交接班導引律設計

考慮初末制導的彈道交接班。在彈道交接點，核心思想是使加速度矢量連續。這可以理解為使得交接班加速度

(41)

為一個連續函數。其中：ajj(t)為導彈的加速度矢量，v(t)為導彈的速度矢量。若能夠使得ajj(t)交接班開始時刻等于初制導結束時刻的加速度指令,在交接班完成時等于末制導所需的加速度指令,則完成導彈中末制導的交接班。

基于以上思想，將交接班看作是從第i條彈道到第j條彈道的過渡。定義交接班導引律為[9]

ajj(t)=aj(tb)+(T+t0-t)[ai(t0)-aj(tb)]/T

(42)

式中，ai(t0)、aj(tb)分別為第i條彈道和第j條彈道的指令加速度。t0為交接開始時間，T為交接班時間。

4 載機發射模塊數學模型

在這里，建立簡化的發射控制模塊數學模型，僅簡要描述其對發射的控制，數學公式如下

(43)

式中，SF為發射狀態字，0表示不發射攔截彈，1表示發射攔截彈；Rm為載機與目標的相對距離測量值；Rb為攔截彈允許發射最遠距離。

5 仿真分析

假設在傳感器理想的情況下，來襲導彈狀態信息及攔截導彈飛行參數都可以準確獲得。反導攔截彈各項參數由Missle Datcom軟件計算得到，來襲導彈為某型雷達制導空空導彈，在Matlab/Simulink中對載機反導場景進行仿真。

來襲導彈攻擊態勢：來襲彈與載機初始高差為2km，初始斜距為6.4km，來襲彈尾追攻擊載機。

攔截態勢：載機在距來襲彈6km處發射反導攔截彈對來襲導彈實施攔截。

仿真條件設置：載機水平勻速飛行，初始位置(0，10000，0)m，初始速度為0.8Ma；來襲導彈初始位置(-6000，12000，1000)m，初始速度為0.8Ma。載機初始彈道偏角為0°，來襲彈初始彈道偏角0°、初始彈道傾角為0°。用于末制導律計算的攔截彈與來襲彈的動力學一階時間常數均取為0.1s。仿真曲線如圖2～圖7所示。

圖2 側向彈道Fig.2 Lateral trajectory

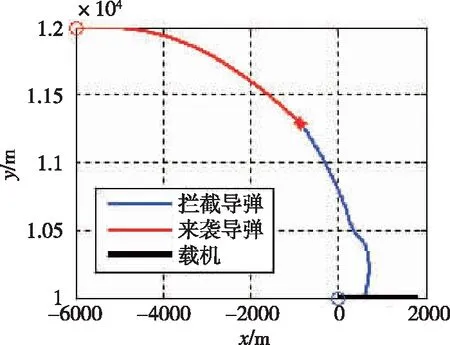
圖3 縱向彈道Fig.3 Longitudinal trajectory

圖4 側向過載Fig.4 Lateral acceleration

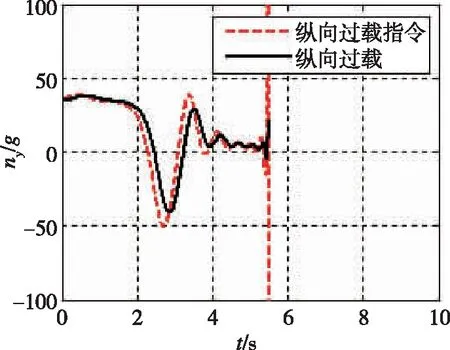
圖5 縱向過載Fig.5 Longitudinal acceleration

圖6 攔截彈速度Fig.6 Velocity of the interceptor

圖7 零控脫靶量Fig.7 Zero-effort misses distance

從圖6中可以看出，初制導轉彎段速度減小，原因是導彈推力和空氣動力的合力與速度方向相反。轉彎段速度較小可以減小導彈需用過載，實現快速轉彎。從圖5中可以看出，攔截彈在進入末制導后以較大的縱向過載使滑膜快速趨近0，到達滑膜后以較小的過載使得ZEM維持在0附近。制導末端tgo趨近于0導致過載指令變化很大。采用本文給出的復合制導律，攔截彈最終的脫靶量為0.2m，能夠對來襲彈實施直接碰撞，同時攔截成功時碰撞點距載機超過1km，能夠保證載機的安全。

6 結論

本文主要研究了反導攔截彈越肩發射的復合制導規律，給出了轉彎段導引律和變結構末制導律，數字仿真結果說明，這種復合制導規律能夠實現載機對來襲導彈的自衛攔截。

基于零控脫靶量的末制導律需要攔截彈的剩余飛行時間、來襲彈機動加速度等信息，這就給小型化攔截彈與載機的探測裝置及估計算法提出了較高的要求，工程上若要實現還需要進一步研究。同時，未來需要進一步考慮在無法準確獲得敵方導彈狀態信息時如何進行估計，本文忽略了許多非線性因素，在更加貼近實際的作戰場景中仍需要深入研究。