區間變時滯系統的時滯相關魯棒非脆弱H∞控制
宋 睿,張合新,吳玉彬,張憲宇,曹建
(1. 火箭軍士官學校,濰坊 262500;2. 火箭軍工程大學,西安 710025;3. 中國人民解放軍96713部隊,上饒 334102)
0 引言
現實世界的許多動力學模型系統,如網絡控制系統、過程控制系統以及核反應堆控制系統等,在數據和物質的傳輸過程中,都包含非常明顯的時滯。在眾多的時滯類型中,區間變時滯更具代表性,它的時滯下界不一定為0,且時滯處于一個變化的區間之內,常見于化學反應器、內燃機和網絡控制等工程實際應用中。因而近年來,區間變時滯系統的穩定性分析成為一個熱門的研究領域[1-29]。
針對區間時滯系統的穩定性分析,最常見的方法是采用基于時域內直接構造L-K(Lyapunov-Krasovskii)泛函并結合線性矩陣不等式(Linear Matrix Inequality,LMI)來實現;針對其鎮定問題,一般采用狀態反饋的形式來實現。文獻[2-9]討論了在狀態反饋控制器作用下系統的鎮定問題,但所給出的控制器無論是無記憶或者有記憶還是H∞控制器,都要求能夠精確實現,不具有魯棒性。在控制器的設計實現中,由于硬件(如A/D、D/A轉換)和軟件(如計算截斷誤差)等原因,控制器不同程度上存在一定的不確定性[10]。Keel等[11]指出,當控制器參數存在攝動時,常規的魯棒控制器表現出高度的脆弱性,從而造成閉環系統的性能下降甚至控制器失效。因此非脆弱控制器的研究便成為大家關注的熱點問題[12-17]。文獻[12-14]和文獻[16-17]分別針對時滯系統的非脆弱H∞控制問題和非脆弱保性能控制問題進行了深入研究。在這些研究中,主要圍繞如何降低所得結論的保守性和滿足一定的性能指標而展開。由于時滯相關條件相比時滯無關條件具有更小的保守性,因此,如何選取合適的L-K泛函和界定條件,進一步得到保守性更小的時滯相關條件,進而設計有效的控制器,便成為目前時滯系統穩定性分析與控制綜合的重點問題。
本文針對一類區間變時滯不確定系統,提出了一個形式簡單的保守性更低的時滯相關有界實判據。該判據借鑒時滯中點法[16]的思想,把時滯區間分割成兩等份,針對每一分割區間構造新的L-K泛函,并采用新的積分不等式和互凸組合技術給出不包含任何多余參量的LMI形式結論。在此基礎上設計了魯棒非脆弱控制器。最后把該控制器應用于垂直起降(Vertical Take-Off and Landing,VTOL )直升機的飛行控制當中,仿真結論表明,所推導的有界實判據相比已有文獻結論具有更低的保守性,所設計的控制器相比一般魯棒控制器具有更好的鎮定效果和明顯的非脆弱性。
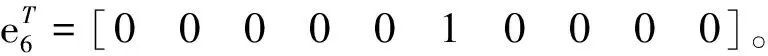
1 問題描述
考慮如下一類具有區間變時滯的線性系統
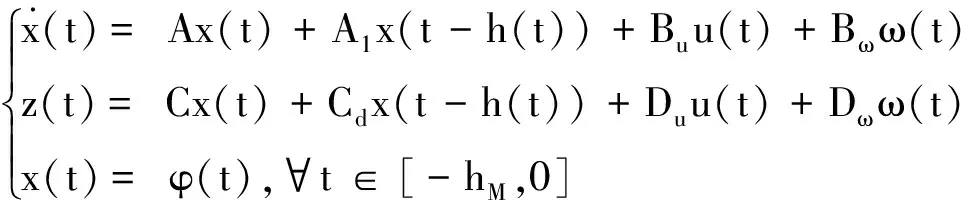
(1)
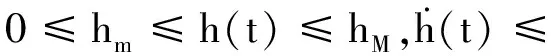
針對系統(1)定義如下性能指標
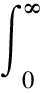
(2)
其中,γ>0為給定標量。
本文主要目標是在外部干擾作用下,設計一個狀態反饋非脆弱H∞控制器
u(t)=(K+ΔK)x(t)
(3)

使得滿足以下2個條件:
1)ω(t)=0時,由式(3)構成的閉環系統(1)漸近穩定;
把非脆弱控制器(3)代入系統(1),則閉環系統為
(4)
其中,Ak=A+BuK+BuΔK,Ck=C+DuK+DuΔK。
為了方便穩定性判據的證明,現將下一步需用到的引理歸納如下:
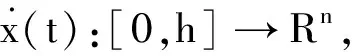
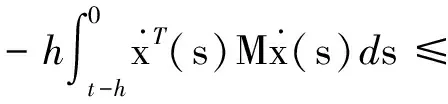
引理2[25]假定任意的正定矩陣M=MT>0,標量h>0和向量函數:x(t):[0,h]→Rn,則有以下不等式成立
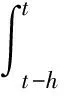
引理3[28]假定任意的正定矩陣M=MT>0,標量0≤α,ε≤1,hm≤h(t)≤hM和向量函數:x(t):[0,h]→Rn,則有以下不等式成立
其中
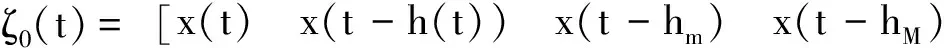
引理4[17]給定具有適當維數的矩Q=QT,H,E和R=RT,則有Q+HF(t)E+ETF(t)THT<0,對任意滿足F(t)TF(t)≤R的F(t)成立的充要條件是存在?>0,使得:
Q+?-1HHT+?ETE<0
2 時滯相關有界實判據
定理1對于給定的標量hm、hM和λ1、λ2(λ1>λ2),若存在正定對稱矩陣Pi(i=1,2,3,4,5),Q1,Q2,U1,U2,Xj,Rj(j=1,2,3,4),使得如下LMIs成立:
Φ=(Φi,j)10×10<0
(5)
則系統(4)在非脆弱控制器(3)的作用下不僅漸近穩定,而且在零初始條件下具有給定的H∞擾動抑制水平γ。其中
Φ13=X2,Φ14=0,Φ15=2P2+hmR2,
Φ16=(2-ε)(hM-hm)R4,
Φ23=-(α-2)X4,Φ24=(1+α)X4,
Φ25=Φ26=Φ27=Φ28=Φ29=Φ210=0,
Φ33=Q2-Q1-X2+(α-2)X4,Φ35=-2P2,
Φ36=Φ37=2P3,Φ34=Φ38=Φ39=Φ310=0,
Φ44=-Q2-(1+α)X4,Φ46=Φ47=-2P3,
Φ45=Φ48=Φ49=Φ410=0,Φ55=-X1-R2,
Φ58=-2P4,Φ56=Φ57=Φ59=Φ510=0,
Φ66=(α-2)X3-(2-ε)R4,Φ67=Φ68=0,
Φ69=Φ610=-2P5,Φ77=-(α+1)X3-(1+ε)R4,
Φ78=0,Φ79=Φ710=-2P5,Φ88=-R1-U1,
Φ89=Φ810=0,Φ99=-(2-ε)R3-U2,
Φ910=-U2,Φ1010=(1+ε)R3-U2,
證明:首先基于時滯中點值hΔ,把時滯區間分成相等的兩部分,即[hm,hΔ]和[hΔ,hM],下面分兩種情況討論。
情形1:當hΔ≤h(t)≤hM時,設計如下L-K泛函
V(x(t))=V1(x(t))+V2(x(t))+V3(x(t))+
V4(x(t))+V5(x(t))
(6)
其中
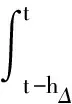
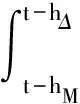
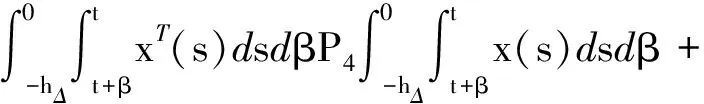
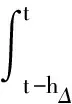
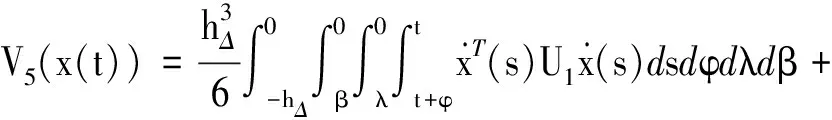
計算L-K泛函V(x(t))沿系統(4)的導數,可得
(7)
其中
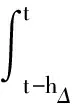
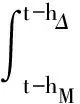
hΔ)Q2x(t-hΔ)-xT(t-hM)Q2x(t-hM)
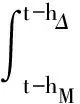
由引理1與引理2可得
(8)
(9)
其中
由引理3可得
(10)
同樣可以得到
(11)
(12)
(13)
(14)
(15)
(16)
(17)
εΓ3+(1-ε)Γ4]ζ(t)
(18)
其中:
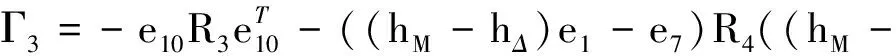
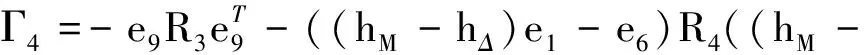
因為0≤α,ε≤1,根據互凸組合技術,如下不等式成立,
α(Γ1+λ1I)+(1-α)(Γ2+λ1I)<0
(19)
ε(Γ3-λ2I)+(1-ε)(Γ4-λ2I)<0
(20)
即
αΓ1+(1-α)Γ2<-λ1I
(21)
εΓ3+(1-ε)Γ4<λ2I
(22)
由于λ1>λ2,合并式(21)、式(22),可得:
αΓ1+(1-α)Γ2+εΓ3+(1-ε)Γ4<(λ2-λ1)I<0
(23)
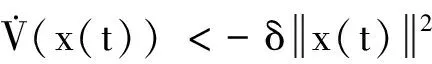
對于給定的γ,考慮性能指標J(ω),則把z(t)Tz(t)-γ2ωT(t)ω(t)加到不等式(18)兩邊,可得
ΨTΨ+αΓ1+(1-α)Γ2+εΓ3+(1-ε)Γ4)ζ(t)
(24)
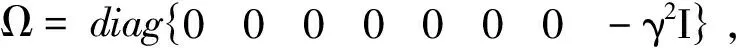
如果:
Ω+ΨTΨ+αΓ1+(1-α)Γ2+
εΓ3+(1-ε)Γ4<0
(25)
那么
(26)
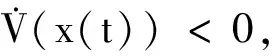
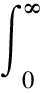
-V(t)|t=∞+V(x(t))|t=0<0
(27)
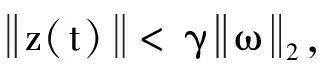
情形2:當hm≤h(t)≤hΔ時,設計如下L-K泛函
V1(x(t))=V11(x(t))+V12(x(t))+
V13(x(t))+V14(x(t))+V15(x(t))
(28)
其中
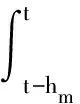
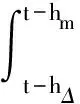
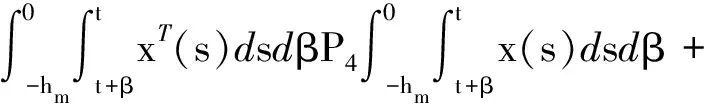
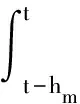
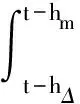
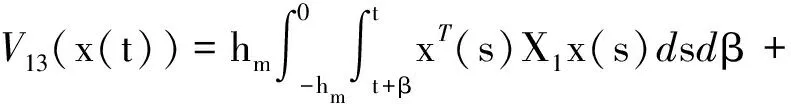
其中
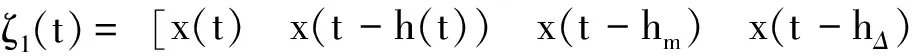
Pi(i=1,2,3,4,5),Q1,Q2,U1,U2,Xj,Rj(j=1,2,3,4),同式(6)中所定義的矩陣。利用同樣的方法,可得
εΓ13+(1-ε)Γ14]ζ1(t)
(29)
其中
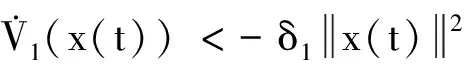
εΓ13+(1-ε)Γ14)ζ1(t)
(30)
如果
Ω+ΨTΨ+αΓ11+(1-α)Γ12+εΓ13+
(1-ε)Γ14<0
(31)
那么
(32)
從而閉環系統在零初始條件下具有給定的H∞擾動抑制水平γ。
由于hM-hΔ=hΔ-hm,對式(18)或式(29)應用引理3,則其等價于式(5)。證畢。
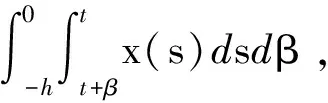
注2 在式(5)中,新的穩定性判據沒有涉及冗余的自由權矩陣,只是巧妙地采用新的積分不等式來界定LKF導數產生的交叉項,并利用極少數自由矩陣來表示相關項之間的關系,因此減少了理論推導和計算上的復雜性,從而降低了結論的保守性。
注3 在式(10)、式(11)和式(14)中,互凸組合處理技術[22]作為一種非傳統方法用來更有效地界定LKF導數產生的交叉項,可以得到保守性更低的穩定性結論。
3 非脆弱H∞控制器的設計
基于時滯相關有界實判據,設計非脆弱H∞控制器。
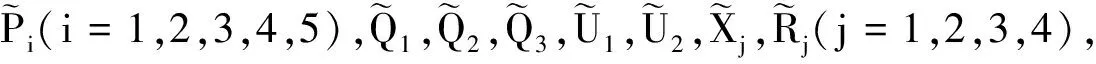
(33)
則不確定系統(1)在非脆弱控制器(3)的作用下不僅漸近穩定,而且在零初始條件下具有給定的H∞擾動抑制水平γ,且控制器增益K=YΞ-T。其中
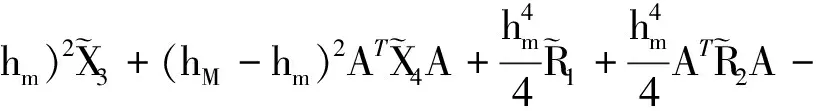
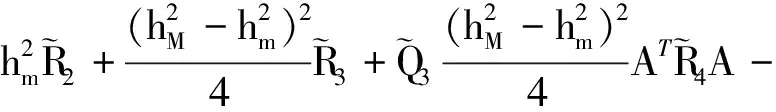
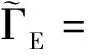
證明:由于定理1中式(5)給出的條件為非線性矩陣不等式,不能直接得到控制器的解。下面給出控制器的設計方法,首先將式(5)中的不確定項(即含ΔK項)分離,即
(34)
其中,Φ′為Φ中分離不確定項(含ΔK項)所得結果。由引理4可得
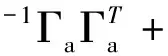
(35)
其中
進而對式(35)應用Schur補可得
(36)
令T1=T2=Ξ-1,其中Ξ為非奇異矩陣,對式(36)兩邊左乘Ψ,右乘其轉置,其中

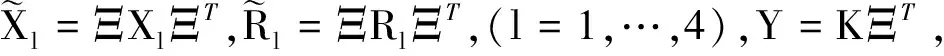
4 數值仿真與比較
下面通過2個數值例子仿真來比較說明本文所提出的時滯相關有界實判據和基于此設計的魯棒非脆弱控制器都在不同程度上改善了已有文獻的結論。其中,最大允許時延 (Maximum Allowable Delay Bound,MADB) 定義為保證系統穩定的最大允許時滯上界值,是時滯系統穩定性結論保守性最普遍的衡量標準;最低允許性能指標 (Minimum Allowable Performance Inde,MAPI) 定義為保證系統穩定的最小允許性能指標值,是時滯系統在零初始條件下所具有H∞擾動抑制水平的衡量標準。
例1首先考慮一類具有區間變時滯的線性系統,形如式(1)所示,其系統參數如下
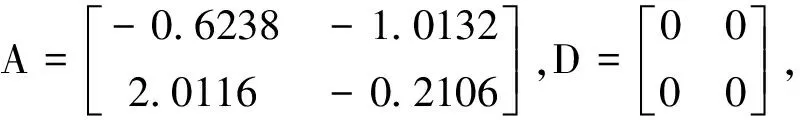
在該數值例子中,考慮2個性能指標,即H∞性能指標γ和MADB值hM。根據定理1,當時滯變化率μ=0和hm=0時,針對不同的H∞性能指標γ,表1仿真給出了相應的MADB值;針對不同的MADB值,表2仿真給出了相應的H∞性能指標γ。
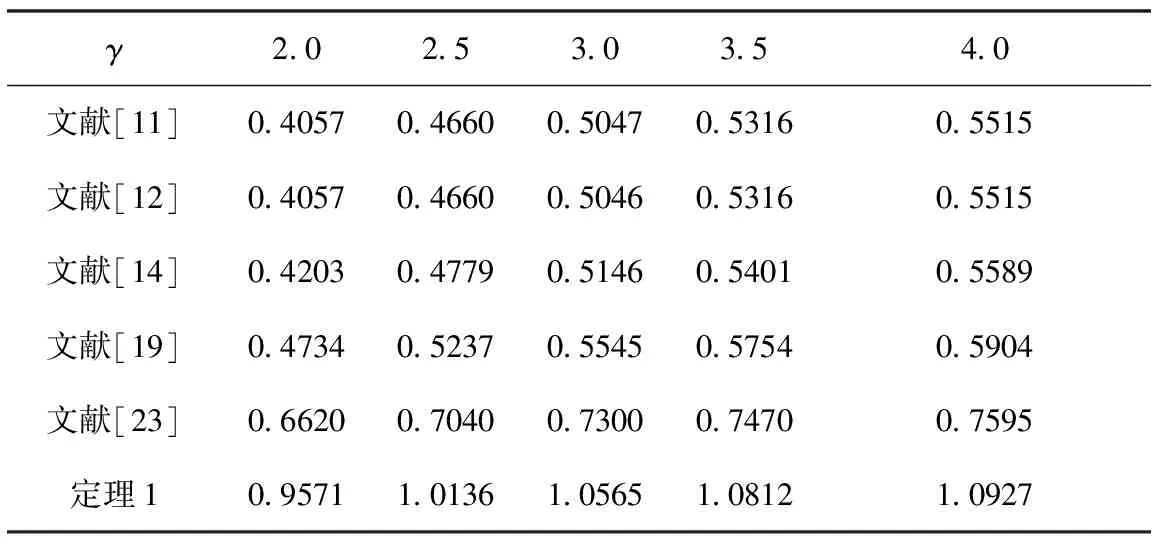
表1 針對不同的H∞性能指標γ,不同方法仿真給出的MADB值hM
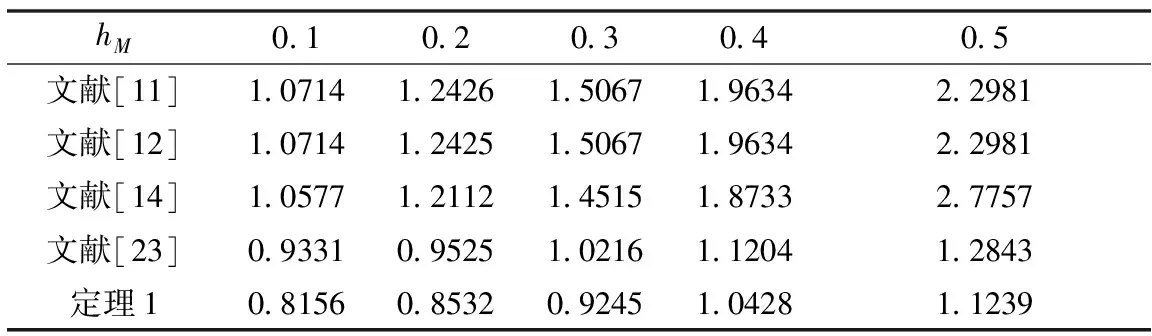
表2 針對不同的MADB值hM,不同方法仿真給出的MAPI值γ
通過比較表1和表2可以發現,對于指定的H∞性能指標γ,由定理1可以得出相應的MADB值。相比文獻[11-12,14,19,23],本文所提出的時滯相關有界實判據擴大了系統穩定的最大允許時滯上界范圍,具有更低的保守性;另一方面,對于指定的MADB值hM,也可以求得相應的MAPI值。相比文獻[11-12,14,23],本文所提出的判據可以獲得保證系統穩定的更小更佳H∞性能指標γ值。
例2下面以VTOL直升機為研究對象進行仿真。VTOL直升機的垂直起降控制過程是一種典型的含有時滯的動態控制系統[18],其模型可描述為
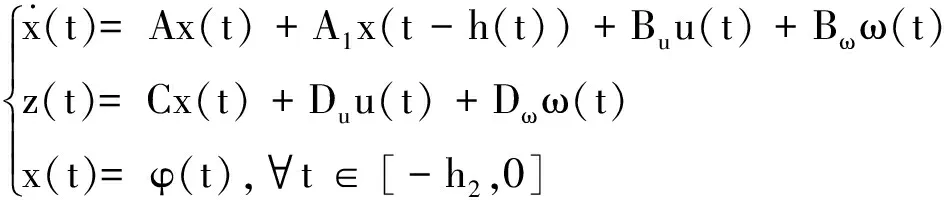
(37)
其中

在不加外部控制(即u(t)=0)時,該控制系統的開環響應曲線如圖1所示,顯然系統是不穩定的。
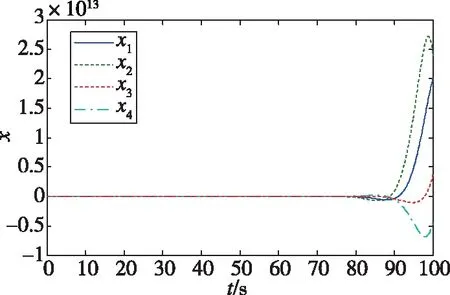
圖1 VTOL系統狀態開環響應曲線Fig.1 State response of the open-loop system
為了說明本文所設計魯棒非脆弱H∞控制器的優越性,下面以VTOL系統在不同控制器作用下的鎮定性能來分析比較。
首先考慮控制器不存在外部干擾和增益攝動的情況。此時攝動參數Da和Ea均為0,取γ=0.9716,設時滯下界hm=0,hM=7,由定理2可得一般魯棒控制器增益矩陣為:
在K1作用下,系統狀態響應曲線如圖2所示。
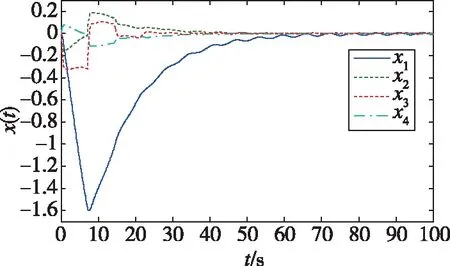
圖2 一般魯棒控制器下系統狀態響應曲線Fig.2 State response of the close-loopsystem under general robust controller
其次考慮控制器存在外部干擾和增益攝動的情況。假設外部干擾為幅值0.1的正弦信號,控制器增益攝動參數Da和Ea均不為0,取γ=0.9716,針對hM=7的定常時滯進行仿真,其中攝動參數取為
擾動矩陣Fa∈R2×2,由定理2可得相應的魯棒非脆弱控制器增益矩陣為
在K2作用下,系統狀態響應曲線如圖3所示。
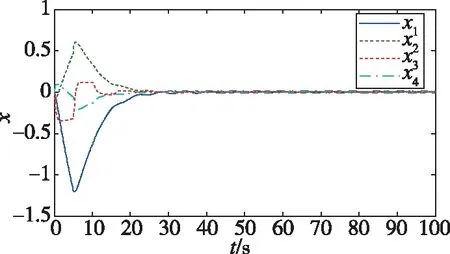
圖3 魯棒非脆弱控制器下系統狀態響應曲線Fig.3 State response of the close-loop systemunder the non-fragile controller
以狀態x1(t)為研究對象,圖4比較給出了相同條件下,一般魯棒控制器和非脆弱控制器的鎮定效果。
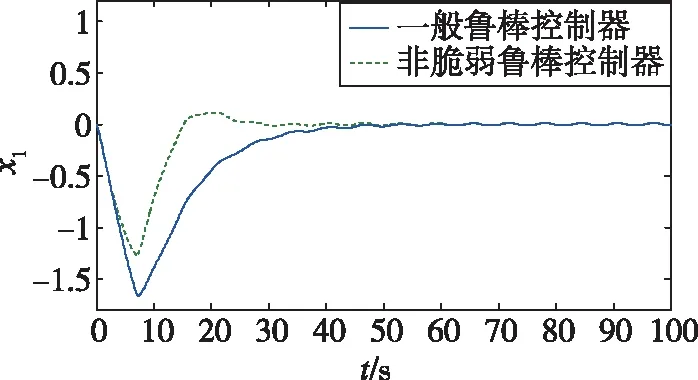
圖4 不同控制器作用下的狀態x1響應曲線Fig.4 Statex1response of the close-loopsystem under different controllers
由圖2~圖4可以看出,在非脆弱控制器K2作用下,系統狀態能夠獲得更佳的性能指標,且容許控制器增益的攝動;而在一般控制器K1的作用下,系統狀態表現出明顯的脆弱性,振蕩較大,收斂較慢。
5 結論
本文對一類區間變時滯線性系統的時滯相關魯棒非脆弱H∞控制問題進行了研究,其創新性體現在如下3個方面:
1)采用時滯中點分割法和互凸組合技術并結合新的積分不等式對泛函導數產生的交叉積分項進行巧妙處理,進而獲得有效結論;
2)獲得了LMI形式的時滯相關有界實判據和非脆弱H∞控制器。該控制器無需任何的參數調整和迭代處理,只需通過LMI的可行解即可得到控制器的參數表達式;
3)將控制器應用于VTOL直升機的飛行過程,通過仿真來進一步說明所設計的控制器相比一般魯棒控制器具有更好的鎮定性能和非脆弱性。

