基于RTS濾波的GPS+BDS 非差非組合PPP/INS緊組合模型

遲皓婧，高周正，楊 凱，閔 于，程佳貝

(中國地質大學(北京)土地科學技術學院，北京 100083)

0 引言

連續、可靠、穩健的高精度位置服務是當前無人駕駛的基本需求。然而，全球定位系統(Global Positioning System，GPS)標準服務作為當前主要的位置服務手段，其定位精度低，且在動態情況下難以提供連續、穩健的位置結果[1]。目前，可用的基于GPS的高精度定位技術主要包括實時動態定位(Real-Time Kinematic，RTK)[2]和精密單點定位(Precise Point Positioning，PPP)[3]。其中，RTK是基于雙差模式的基線解算得到高精度位置結果，但RTK的定位精度隨基站與流動站間的基線距離的增加而快速降低。因此，常規RTK技術只能在小范圍內提供高精度位置服務[1,4]，這顯然難以滿足當前用戶對廣域作業區域的需求。而PPP技術，基于非差模式，采用國際GNSS服務(International GNSS Service，IGS)組織提供的精密軌道/鐘差產品[5]和經典模型[1,3]來改正GPS的觀測誤差，并將未模型化的誤差項和部分模型改正后的殘余誤差進行參數化建模，通過參數估計的方法實現了單臺接收機的cm級定位解算。因此，PPP較RTK具有更廣泛的應用前景和科研價值。

然而，PPP的定位性能受用戶環境影響顯著。在動態復雜環境下(如市區大型建筑附件、隧道、立交橋等)，常出現部分或全部衛星丟失，這將明顯降低PPP定位精度和連續性[1]。近些年，部分學者基于周跳修復、非差模糊度固定等理論對加快PPP重收斂進行了研究[6-7]，但這些方法一方面主要基于高質量的仿真數據進行驗證，不能完全反映實際情況；另一方面，這些方法不能提供衛星丟失期間的位置信息[1,8]。部分學者提出了GPS與慣性導航系統(Inertial Navigation System，INS)組合技術[8-11]可有效提高GPS定位性能，特別是緊組合模式能充分利用復雜環境下少于4顆的GPS衛星信息[8]。為此，本文采用基于GPS+BDS雙系統觀測數據進行PPP/INS緊組合的方案來解決上述問題。其中，采用GPS+BDS雙系統數據，可有效提高動態應用中的可用衛星數，從而達到改善GPS衛星部分失鎖情況下的定位幾何強度(Position Dilution of Precision，PDOP)[13]、加快收斂速度和提高定位精度的目的[1]。INS則可通過力學編排處理慣性測量單元(Inertial Measurement Unit, IMU)輸出的線運動信息和角運動信息，為用戶提供連續的具有短期高精度的位置信息[1,12]。然而，IMU誤差的時間累加性導致INS在衛星失鎖期間的定位精度隨時間的增加而發散[1,14]。為此，本文將RTS濾波(Rauch-Tung-Striebel Filter)理論[8,15]應用到PPP/INS緊組合算法中，以此來進一步提高動態定位性能。

本文詳細介紹了基于RTS濾波的GPS+BDS 非差非組合PPP/INS緊組合模型，并利用車載實驗數據分析了不同定位方法的定位、測速、定姿性能。

1 函數模型

1.1 GPS+BDS非差非組合PPP函數模型

與傳統的基于雙頻載波和偽距的消電離層組合PPP模型不同，非差非組合PPP采用雙頻原始觀測值形成基本觀測方程。同時采用GPS和BDS觀測數據時，其對應的觀測方程可表示為[1,8,16]

(1)

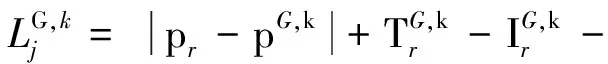
(2)

(3)

(4)

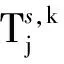
需要注意，因信號結構、信號頻率等差異，同一臺GPS+BDS雙系統接收機，分別進行GPS PPP和BDS PPP解算得到的接收機鐘差并不相同。兩者之間的差異稱為系統間偏差(Inter-System Bias, ISB)[1,7]，其具有時域上的穩定性。因此，在參數估計時，將BDS的接收機鐘差表示為

tB,r=tG,r+ISBB-G

(5)

式中，ISBB-G表示BDS與GPS之間的系統間偏差。

此外，與傳統PPP采用消電離層組合消除電離層誤差的策略不同，非差非組合PPP中將模型改正后的電離層殘余誤差作為參數進行估計[8]。由于非差非組合PPP中待估參數個數較多，直接估計電離層參數會降低PPP解的強度和定位精度。因此，通過增加電離層虛擬觀測的方式來提高PPP解的強度。首先，根據電離層的頻率相關性特性，將GPS和BDS第二頻率上的電離層延遲表示成第一頻率上的電離層延遲

(6)

(7)

然后，將上述電離層誤差改正到偽距和載波觀測值中，并將殘余誤差建模為隨機游走過程，即

(8)

(9)

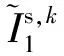
同時，當前衛星鐘差的解算策略使得偽距硬件延遲被消電離層組合的鐘差吸收，因此在進行消電離層組合PPP解算時，可以忽略偽距硬件延遲的影響[8]。而在非差非組合PPP模式下，則需考慮偽距硬件對PPP的影響。其中，衛星端的偽距硬件延遲可采用IGS提供的衛星碼間偏差(Differential Code Bias，DCB)產品進行改正，而接收機端的硬件延遲則以DCB的形式進行參數化估計[1,13]

(10)

(11)

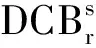
綜上，GPS+BDS非差非組合PPP的觀測方程將由原始偽距和載波觀測方程(式(1)～式(4))、電離層虛擬觀測方程(式(8)～式(9))和接收機DCB虛擬方程(式(11))組成。觀測值的先驗權則采用經典的衛星高度角定權法。待估參數則包括接收機位置、鐘差、系統間偏差、對流層濕延遲殘余誤差、電離層模型改正殘余誤差和每個頻率上的模糊度。最終采用序貫最小二乘或擴展Kalman濾波[12]可實現非差非組合PPP的參數估計。

1.2 非差非組合PPP/INS緊組合函數模型

雖然PPP具有長期高精度定位特性，但在動態應用中，衛星信號常因大型建筑物、立交橋、樹蔭、隧道等遮擋而丟失，引起PPP定位不連續和降低PPP的定位精度。而INS可利用IMU測量的載體角運動和線運動信息，提供連續的且不依賴用戶環境的導航結果，但INS的結果因IMU期間誤差的累加而不斷發散。因此，文中采用PPP與INS組合，綜合利用PPP和INS的優點，克服單一系統的缺點，以獲得高精度、連續的定位結果。通常，利用Kalman濾波理論[15,17]構建非差非組合PPP/INS緊組合的觀測方程和狀態方程

Zk=Hkxk+ηk,ηk～N(0,Rk)

(12)

xk=Φk,k-1xk-1+εk-1,εk-1～N(0,Qk-1)

(13)

式中，Zk表示量測新息向量；Hk表示設計系數矩陣；ηk表示零均值且方差為Rk的量測噪聲;xk表示狀態參數向量；Φk,k-1表示狀態轉移矩陣；εk-1表示零均值且方差為Qk-1的狀態參數驅動噪聲。其中，觀測新息向量可表示為

(14)

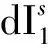
在進行INS預測時，通過INS更新的IMU中心處的位置和速度信息(通過INS力學編排更新)與衛星位置和速度信息(由精密軌道計算)預測理論上的偽距、載波和多普勒觀測。由于IMU中心與接收機天線相位中心不一致，因此在數據處理時需要考慮因測量中心不同而引起的桿臂誤差，即先將IMU中心的位置和速度轉換到接收機天線相位中心[8-12]

(15)

(16)

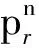
PPP/INS緊組合的狀態參數則由兩部分構成，即PPP中的全部參數和INS的全部參數

(17)

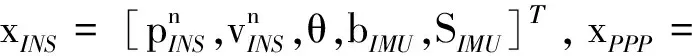
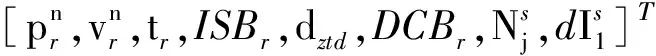
據此，對式(14)在式(17)處進行泰勒級數展開，即可得到Hk陣。Φk,k-1則可根據狀態參數的隨機模型獲得。本文采用PSI誤差角模型描述緊組合中的位置、速度和姿態變化；將IMU傳感器誤差建模成一階高斯馬爾科夫過程，將對流層/電離層殘余誤差、接收機DCB和系統間偏差建模成隨機游走過程；將載波模糊度建模成隨機常數[1, 8]。據此，可實現狀態預測[15, 17]

xk,k-1=Φk,k-1xk-1

(18)

(19)

和狀態更新

xk=xk,k-1+Kk(Zk-Hkxk,k-1)

(20)

(21)

式中，Kk和I分別表示增益矩陣和單位矩陣。

1.3 RTS濾波函數模型

由于Kalman濾波是利用當前時刻(k)的觀測數據以及k之前的狀態信息(xk-1和Pk-1)實現對當前狀態參數信息的估計(xk和Pk)。在數據后處理時，可采用平滑濾波器算法以充分利用GNSS和INS所有可用觀測新息，實現正向濾波解和方向濾波解的最優組合，達到改善GNSS/INS組合導航定位性能的目的。

本文采用RTS固定平滑區間的線性平滑濾波器，不須直接進行Kalman濾波反向解算，即能實現等效于正向濾波解與反向濾波解的最優組合。RTS的數學模型可表示為[12, 15]

xk/N=xk/N+Jk(xk+1/N-xk+1/k)

(22)

(23)

(24)

式中，N表示平滑區間內歷元總個數，k=N-1,N-2, …表示區間歷元時刻。由于PPP/INS緊組合中的航向角觀測性較弱，通常航向精度比橫滾角和俯仰角精度差[1]。而采用RTS濾波，可明顯提高航向角精度。

1.4 算法基本架構

基于RTS濾波的GPS+BDS PPP/INS緊組合算法流程如圖1所示。首先，利用PPP解算的位置和速度、IMU的靜態數據和IMU性能參數(表1)進行姿態對準和濾波器初始化，包括Kalman濾波器的初始狀態向量、對應的先驗方差和狀態噪聲矩陣[1]。根據初始狀態信息，利用獲取的GPS+BDS/INS數據進行PPP/INS解算。由于IMU數據采樣率遠高于GPS/BDS，通常先利用經過誤差補償后的IMU數據進行INS力學編排[9]解算，獲取當前IMU歷元的載體信息，并利用Kalman狀態更新方程，計算當前狀態向量對應的方差-協方差矩陣。然后，進行GPS/BDS可用性檢測。若當前IMU歷元沒有可用的GNSS數據，則直接輸出INS力學編排更新的導航結果；若當前歷元GNSS數據可用，則進行PPP/INS緊組合解算，并將解算的IMU誤差及其他導航參數的改正新息反饋給下一個IMU歷元，以此進行IMU誤差補償和導航信息修正[8-12]。所有歷元完成解算之后，利用保存的正向Kalman狀態向量及方差信息，根據式(22)～式(24)進行RTS平滑。

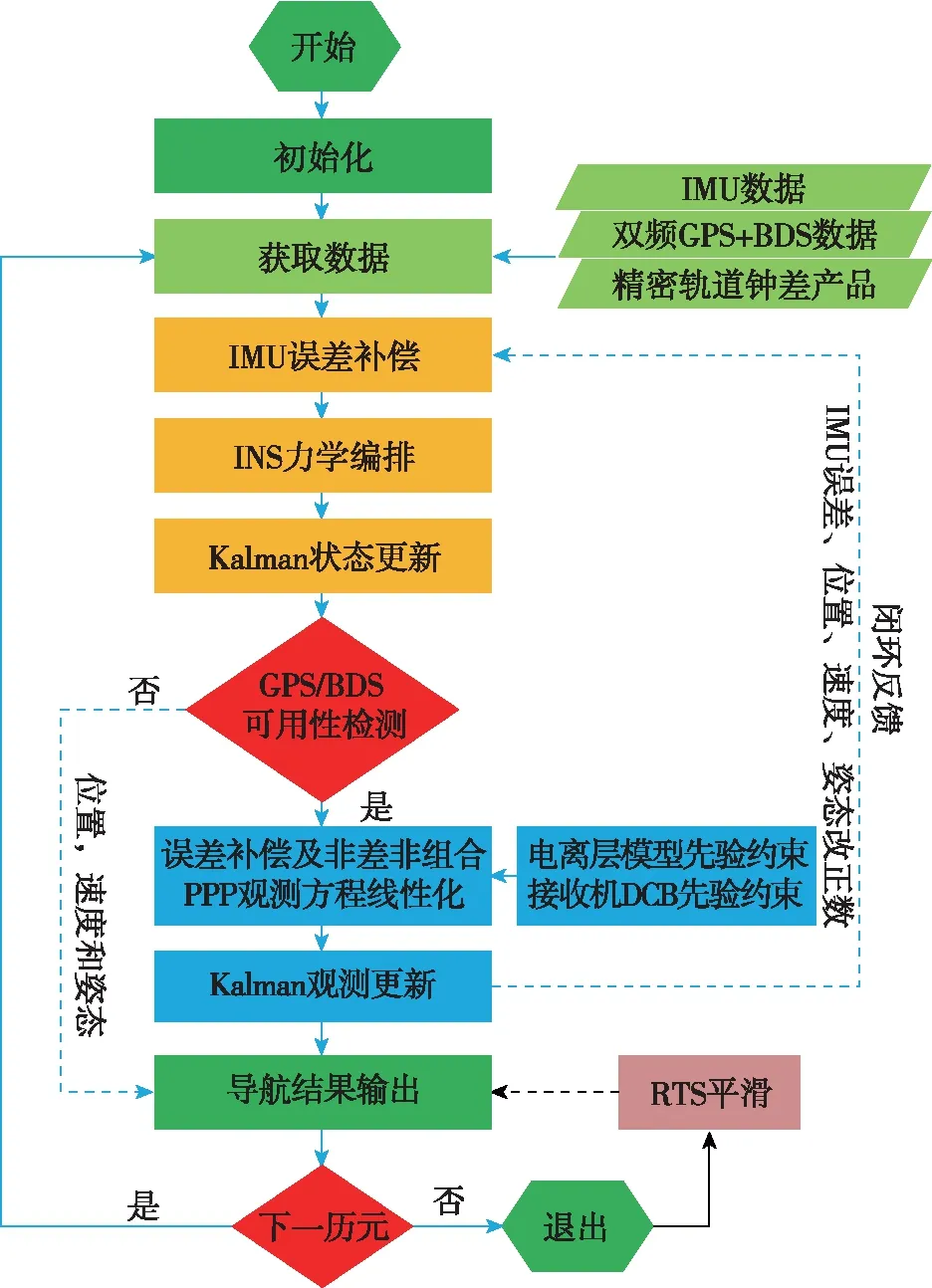
圖1 基于RTS濾波的GPS+BDS PPP/INS緊組合算法架構圖Fig.1 Algorithm structure of the RTS smootherbased GPS+BDS PPP/INS tight integration

2 試驗論證與結果分析

為驗證本文的GPS+BDS非差非組合PPP/INS緊組合模型性能并分析其在觀測條件良好和衛星信號短時間內完全失鎖時的定位性能，本文對2013年在武漢市采集的一組車載GPS+BDS/INS數據(天寶R9接收機和武漢邁普時空POS1100 低精度IMU(http://www.whmpst.com/cn/imgproduct.php?aid=38)和諾瓦泰FSAS光纖IMU(https://www.novatel.com/assets/Documents/Papers/FSAS.pdf)車載數據)進行處理分析(IMU參數和測試軌跡圖分別如表1和圖2所示)。其中，GPS數據采樣率為1Hz，2款IMU數據采樣率為200Hz。在測試之前，以IMU為中心，精確測量接收機天線至IMU的桿臂值。

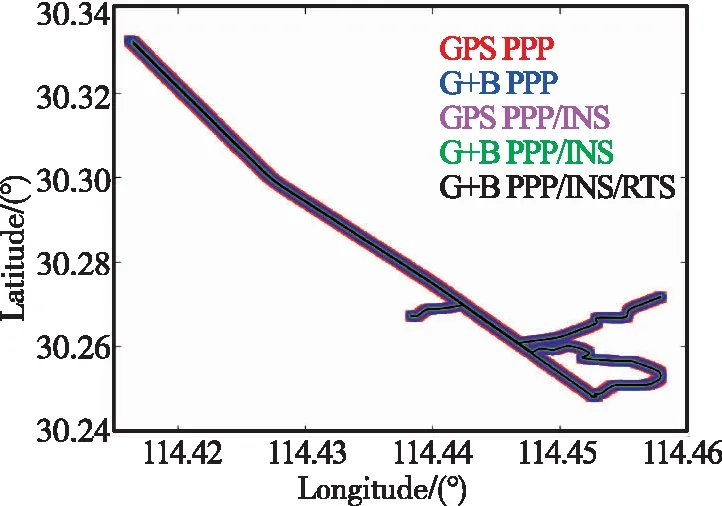
圖2 不同定位模式下的車載測試軌跡圖Fig.2 Trajectories calculated by different positioning modes

2.1 數據處理策略與衛星觀測條件

數據處理時，分別采用5種定位方法進行定位解算，即GPS PPP、GPS+BDS PPP、GPS PPP/INS緊組合、GPS+BDS PPP/INS緊組合和基于RTS平滑濾波的GPS+BDS PPP/INS緊組合。采用武漢大學衛星提供的GPS/BDS精密軌道/鐘差產品，IGS的衛星DCB產品、電離層產品、接收機和衛星天線相位中心偏差產品、極移產品消除軌道誤差、電離層誤差、衛星硬件延遲偏差、接收機和衛星天線相位中心偏差/偏移誤差。采用Saastamoinen天頂延遲模型和全球投影函數(Global Mapping Function，GMF)削弱對流層誤差對定位的影響[18]。其他誤差如地球自轉、相對誤差、固體潮、相位纏繞等均采用經典模型進行修正[1,7]。為剔除低精度觀測值對PPP定位精度的影響，將衛星截止高度角設置為10°。在INS數據處理時，將IMU零偏和比例因子建模從一階高斯馬爾科夫過程進行估計，而劃槳效應、旋轉效應和圓錐效應則采用經典模型進行補償[12]。數據分析時，采用諾瓦泰公司的Inertial Explorer軟件的GPS+GLONASS RTK/FSAS平滑結果作為位置、速度、姿態的參考基準。

圖3和圖4分別表示本次實驗期間所觀測到的GPS衛星和BDS衛星星空圖及其對應的衛星數和PDOP值時間序列圖。據圖3可清晰看出，本次實驗中GPS衛星空間分布要優于BDS。因為，實驗期間，BDS的空間星座主要由5顆GEO衛星、5顆IGSO衛星和4顆MEO衛星構成。這使得通常觀測到的衛星以GEO和IGSO衛星為主，而GEO幾乎成一條直線分布在赤道上空。統計結果表明，采用GPS時，平均可用衛星數和PDOP值為8.5和2.1；采用GPS+BDS時，平均可用衛星數和PDOP值為15.0和1.7。這表明，采用雙系統數據時，可明顯改善可視衛星數和定位幾何強度[13]。例如，在65min附近，單GPS的可用衛星數是4，這時其PPP定位精度將明顯降低(圖5)；而采用GPS+BDS時，其可視衛星數增加到10，定位精度也得到明顯改善。

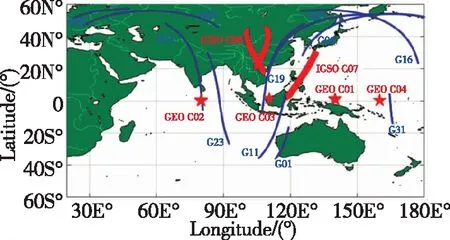
圖3 車載測試中可視GPS和BDS衛星星空分布圖Fig.3 Satellites sky-plot of the visibleGPS and BDS during the test

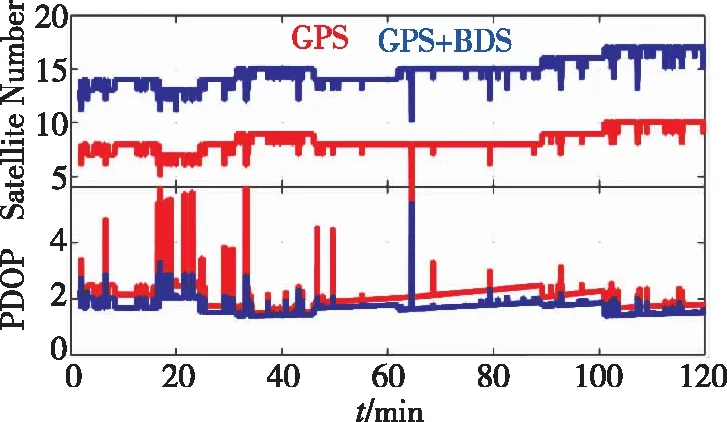
圖4 可視衛星數及對應的PDOP值Fig.4 Visible satellite number and PDOP

2.2 開放天空條件下的定位-測速-定姿性能分析

首先，對開放條件下不同模式的性能進行分析。由于PPP和PPP/INS緊組合需要收斂時間，因此在數據分析時，初始15min數據沒有參與均方根(Root Mean Square，RMS)統計。圖5表示不同定位模式的位置解算結果與參考值作差，并轉換到n系中的位置誤差時間序列圖，其對應的統計結果如表2所示。從中可以看出，在PPP模式下，采用GPS+BDS雙系統數據時，其定位精度(4.9cm、9.6cm、25.1cm)較單使用GPS時(14.0cm、19.9cm、32.3cm)得到明顯改善；在北-東-高3個分量的改善幅度達到65.0%、49.2%和22.3%。其原因，一方面采用GPS+BDS時，可用衛星數大幅增加，同時PDOP明顯改善，從而加快了PPP的收斂速度和提高了定位精度；另一方面，采用雙系統觀測數據，可彌補單GPS觀測不足引起的PPP重收斂(對比圖4和圖5中65min時刻的GPS衛星數和定位誤差變化)。

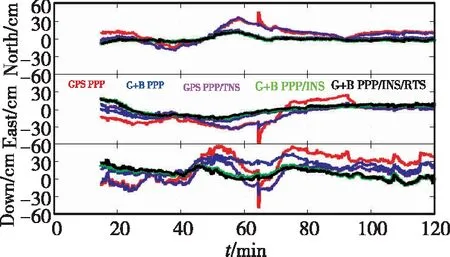
圖5 PPP和PPP/INS的位置誤差時間序列圖Fig.5 Position error time series diagram ofPPP and PPP/INS

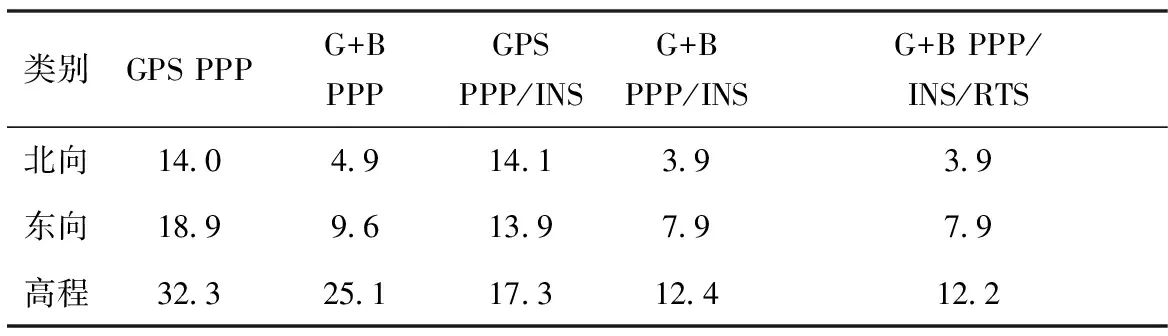
表2 不同定位模式的位置誤差RMS統計結果

在PPP/INS緊組合模式下，BDS對GPS PPP/INS緊組合定位精度的改善模幅度為72.3%、43.2%和28.3%，與PPP模式下基本一致。因為INS對PPP的增強作用，主要表現在3個方面，一方面INS自主定位特性可彌補衛星短時間內失鎖引起的定位結果不連續問題，并在短時間內提供高精度位置結果；另一方面，INS力學編排具有低通濾波特性，可顯著降低GPS/BDS觀測噪聲對定位精度的影響；此外，INS定位精度隨時間的增加而降低，其長期定位精度由GPS/BDS PPP定位性能決定。因此，BDS對PPP和PPP/INS緊組合定位精度的改善效果保持一致。但RTS對衛星觀測條件良好的PPP/INS緊組合的定位精度提高不明顯。此外，BDS對PPP和PPP/INS緊組合定位精度的改善作用，在北向比東向和高程向更明顯。這與實驗開展期間北斗區域系統的衛星星座構成密切相關。

INS對PPP高程方向的定位精度改善比平面明顯。其原因在于，PPP模式下，可視衛星幾乎很少分布在測站天頂方向，使得高程觀測性很弱。而在PPP/INS緊組合中，六軸的IMU傳感器增加了對高程方向的直接觀測，從而使得高程的估計精度大大提高。

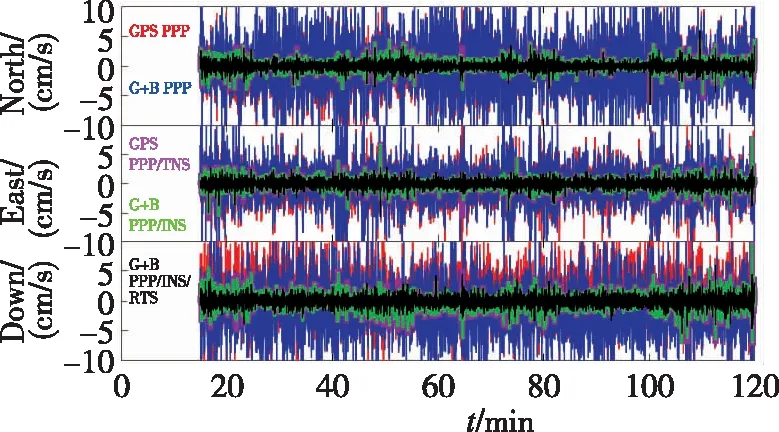
圖6 PPP和PPP/INS的速度誤差時間序列圖Fig.6 Velocity error time series diagram ofPPP and PPP/INS

不同數據處理模式的測速結果如圖6所示，其對應的統計結果如表3所示。圖6中，紅色和藍色線分別表示GPS PPP和GPS+BDS PPP的測速誤差，粉色和綠色線條分別表示與之對應的PPP/INS緊組合測速誤差，黑色線表示基于RTS平滑濾波的PPP/INS緊組合測速誤差。從圖6中可以明顯看出，PPP/INS緊組合的測速精度(粉色和綠色)遠優于基于多普勒觀測的PPP測速結果(紅色和藍色)。而在PPP模式下，采用單GPS數據和采用GPS+BDS雙系統的測速結果精度差異不明顯(小于5mm/s，見表3)。在PPP/INS緊組合模式下，BDS對測速精度的改善亦不明顯(見表3)。而在采用RTS濾波后，測速精度提高顯著。根據表3統計結果可知，北-東-高3個方向的測速精度從GPS PPP模式下的4.5cm/s、3.7cm/s、4.7cm/s 提高到GPS+BDS PPP/INS緊組合模式下的0.8cm/s、0.8cm/s、1.2cm/s，分別提升了82.2%、78.4%和74.5%。而RTS平滑后的測速精度進一步提升了25.0%、12.5%和33.3%，達到0.6cm/s、0.7cm/s和0.8cm/s。

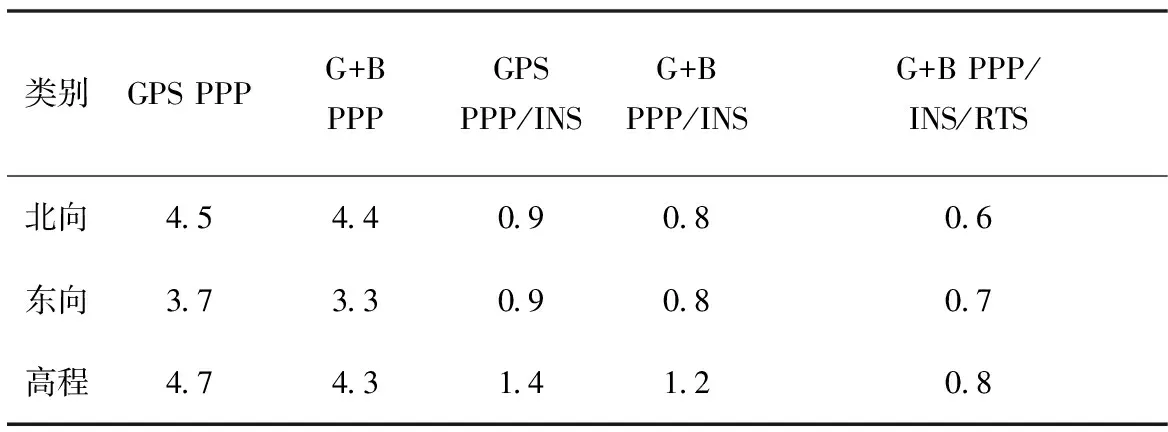
表3 不同定位模式的速度誤差RMS統計結果

因為PPP模式下，測速精度主要取決于多普勒觀測精度。在當前多普勒觀測噪聲條件下，多普勒測速精度只能達到數cm/s的精度[1]。而GPS多普勒觀測精度與BDS多普勒觀測精度基本在同一精度水平，因此即使采用BDS+GPS，測速精度亦沒有顯著改善，這一點與PPP定位不同。而與INS組合之后，可直接利用INS的低通濾波特性，有效消除多普勒噪聲對測速精度的影響。同時，IMU的三軸加速度計形成了對三維速度的直接觀測，從而保證了GPS/BDS與INS融合后，測速精度大幅提升。同時，由于RTS濾波可利用當前觀測歷元之后的所有歷元狀態信息，從而進一步改善了測速精度。

圖7表示三種PPP/INS緊組合模式下的姿態誤差結果，其對應的RMS統計結果如表4所示。從圖7可以看出，PPP/INS緊組合中的姿態精度與采用單GPS(粉色線)或是雙系統GPS+BDS(綠色線)數據幾乎無關。因為，定姿精度與IMU傳感器性能以及載體的機動情況直接相關[1]。而圖2所示的軌跡圖亦表明本次測試的航向機動較弱，且對于同一組GPS或GPS/BDS數據，相同時刻的機動性是相同的。因此，測試中定姿精度主要由IMU性能決定。同時如圖7，航向角(heading)誤差明顯大于橫滾角(roll)和俯仰角(pitch)誤差。因為航向觀測性較弱，在沒有足夠豐富的機動情況下，航向角精度會比其他2個姿態角精度差。但航向角精度在進行RTS平滑之后(黑色線)有了顯著改善。根據表4的統計結果可知，橫滾、俯仰和航向角RMS從GPS PPP/INS緊組合模式下的0.328°、0.102°、0.432°提高到RTS平滑 GPS+BDS PPP/INS緊組合的0.314°、0.084°、0.330°。

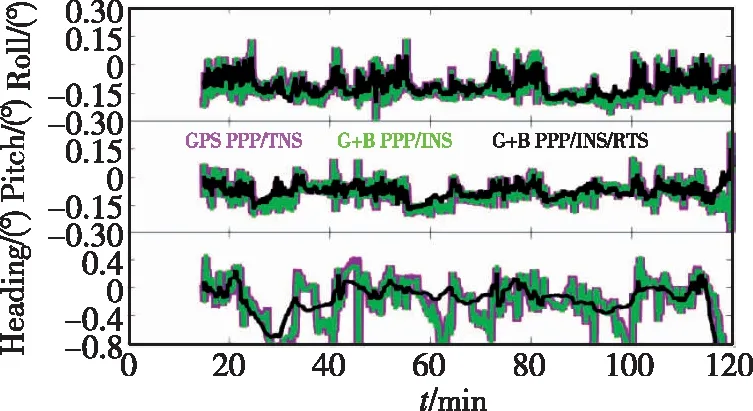
圖7 PPP/INS的姿態誤差時間序列圖Fig.7 Attitude error time series diagram ofPPP and PPP/INS

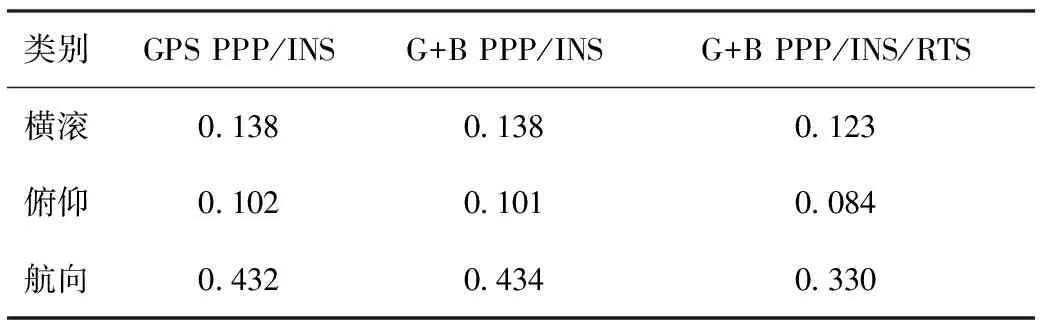
表4 不同定位模式的姿態誤差RMS統計結果

2.3 衛星信號短期失鎖條件下的定位-測速-定姿性能分析

在上述實驗數據的基礎上，通過對原始GPS/BDS觀測數據進行信號失鎖仿真，分析衛星信號短時間失鎖條件下不同模式的性能。在衛星信號失鎖仿真時，每20min設置一次時長為5s的衛星信號全部丟失現象，然后按照五種模式進行數據處理。不同模式下的定位、測速和定姿誤差如圖8～圖10所示。

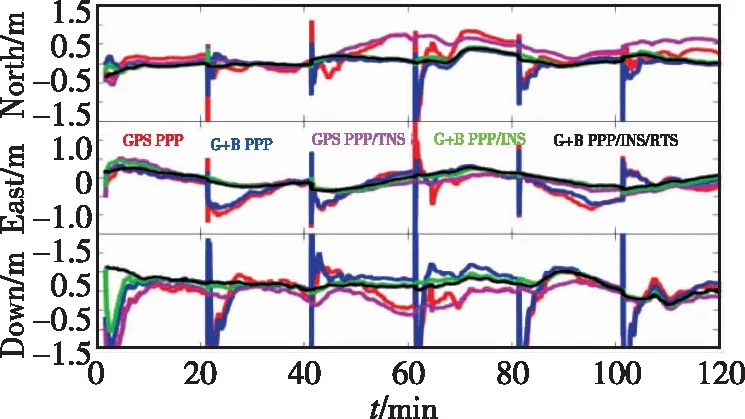
圖8 衛星信號失鎖條件下PPP和PPP/INS的位置誤差圖Fig.8 Position errors of PPP andPPP/INS integrationunder the satellite outage conditions

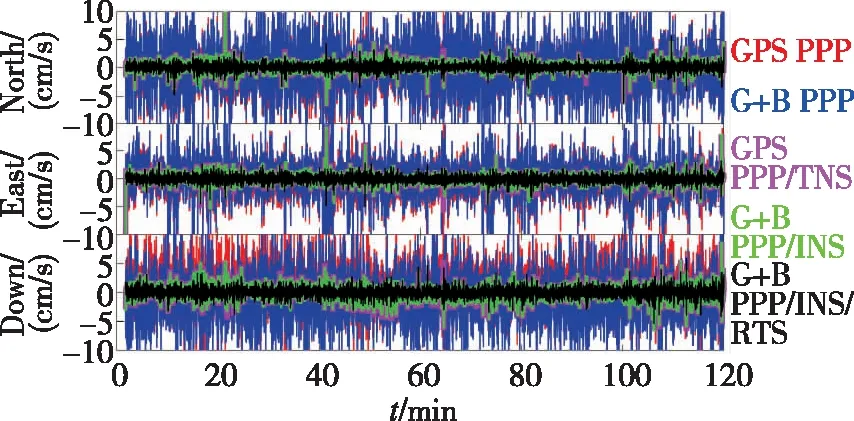
圖9 衛星信號失鎖條件下PPP和PPP/INS的速度誤差圖Fig.9 Velocity errors of PPP and PPP/INS integrationunder the satellite outage conditions

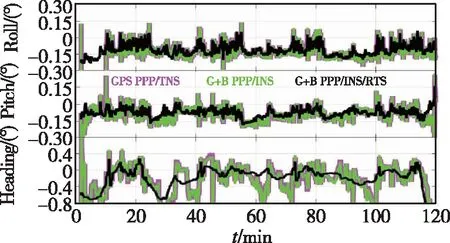
圖10 衛星信號失鎖條件下PPP/INS的姿態誤差圖Fig.10 Attitude errors of PPP/INS integrationunder the satellite outage conditions

從圖8可以看出，每當出現衛星信號完全丟失時，GPS PPP(紅色線)和GPS+BDS PPP都會進行重新收斂(藍色線)。但使用GPS+BDS雙系統數據時(藍色線)，PPP的重收斂速度明顯比GPS PPP(紅色線)快。根據表5的統計結果可知，此時BDS對GPS PPP定位RMS的改善幅度在北-東-高3個方向分別達到了46.1%、14.6%和9.2%。而在PPP/INS緊組合模式下，這種改善幅度為63.6%、13.6%和0.0%。INS對GPS PPP和GPS+BDS PPP的改善幅度為5.5%、46.0%和61.2%。RTS對PPP/INS緊組合的改善幅度為12.5%、5.3%和8.3%。與GPS PPP定位結果相比，使用基于RTS濾波的GPS+BDS PPP/INS緊組合對衛星信號頻繁丟失情況下的定位改善總幅度達到了64.1%、56.1%和66.2%。此外，從圖8可以明顯看出，在衛星信號短時間丟失的條件下，INS可有效改善PPP的定位精度、連續性和可靠性。在衛星丟失期間，PPP無法提供定位結果，而PPP/INS緊組合則可以利用INS的自主定位特性繼續在短期內提供高精度位置信息。同時，RTS濾波可以進一步提升PPP初始化期間和衛星信號丟失期間的定位性能。

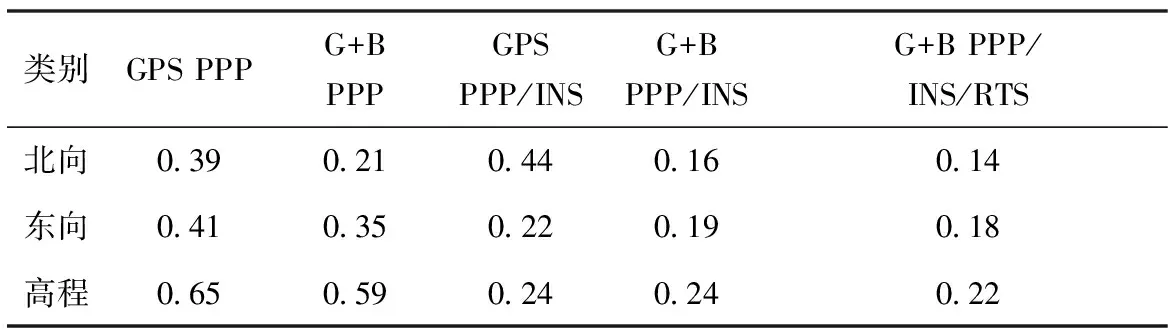
表5 不同定位模式的位置誤差RMS統計結果

對比圖6和圖9可以看出，短時間的衛星信號失鎖并不會影響PPP和PPP/INS緊組合的測速精度。其原因在于，PPP的測速精度主要受多普勒的觀測精度影響；而PPP/INS緊組合的測速精度取決于IMU的性能，在短時間內(5s)，速度的發散幅度很小，可以忽略[1]。同樣，在衛星失鎖期間，PPP無法提供測速結果，而PPP/INS緊組合則可以通過INS力學編排[12]繼續提高測速結果。同理，對比圖7和圖10可以發現，短時間的衛星失鎖對PPP/INS緊組合的定姿精度沒有影響。因為在5s內，POS1100的姿態漂移小于0.03°[1]。

3 結論

本文基于RTS濾波理論和GPS+BDS原始觀測數據，推導了基于RTS濾波的GPS+BDS非差非組合PPP/INS緊組合的函數模型，并通過車載數據和仿真數據分析了該算法的定位、測速和定姿精度。實驗結果表明，BDS能明顯改善GPS PPP的定位精度、連續性和可靠性，且這種改善作用與PPP和PPP/INS緊組合模式下的作用基本一致。在采用相同的GNSS數據時， INS能明顯改善PPP的定位和速度精度。此外，在衛星短時間失鎖期間，BDS、INS和RTS濾波對PPP的定位精度、重收斂速度和初始化定位精度改善明顯，而對測速和定姿精度的影響可以忽略。本文的研究內容和研究成果，在當前室內外一體化高精度位置服務和無人駕駛的大趨勢下，可進一步擴展應用至各與GNSS/INS相關的多源數據融合技術中，具有廣泛的應用價值。