星敏感器安裝誤差標定技術研究

2019-05-16 09:31:32蔡善軍吳亮華胡奇林

導航定位與授時 2019年3期

王欣，蔡善軍，吳亮華，胡奇林

(北京自動化控制設備研究所，北京 100074)

0 引言

星敏感器(以下簡稱星敏)是一類具有獨立自主高精度姿態測量能力的儀器，目前三軸測姿精度可達到角秒級[1]，輸出的慣性姿態誤差不隨時間累積，數據更新率可達5～10Hz。在長航時飛行器應用背景下，可利用星敏高精度的姿態信息修正慣性導航的誤差[2]，實現高精度自主導航。大視場星敏感器技術的發展，使得星敏與慣導系統采取捷聯安裝的方式成為可能。受加工精度的限制，星敏與慣導系統之間的安裝誤差常常能達到角分級[3]。而諸如歲差、視差等因素使恒星方向有微小的變化，從而造成星敏感器的測量誤差，但是它們所造成的誤差是角秒級的[4]。相較而言，星敏安裝誤差成為限制星敏測量精度的主要因素之一。因此，有必要對星敏的安裝誤差建模，并進行標定補償。

目前，星敏安裝誤差標定的方式有兩類：一類是依靠外部基準姿態信息與星敏姿態信息進行比較從而得出安裝誤差角，如文獻[5]提出的一種在高精度星模擬器輔助下的星敏感器安裝誤差標定方法，該方法采用經緯儀提供的外部方位信息，能達到10″的標定精度，但操作過于繁瑣，對設備要求高，不利于在地面實現快速標定；另一類是依靠星敏的測量信息，建立卡爾曼濾波模型，對安裝誤差角進行估計，如文獻[6]、文獻[7]、文獻[8]，但文獻中均未論述慣導姿態誤差與星敏安裝誤差角的關系。

針對上述情況，本文從理論上分析了星敏安裝誤差角與慣導姿態誤差的關系，利用慣導輸出的姿態信息、位置信息以及星敏測量信息構造觀測量，建立了卡爾曼濾波模型，實現了星敏安裝誤差角在地面上的標定補償。

1 參考坐標系

設星敏理想坐標系為O-XcYcZc，載體坐標系為O-XbYbZb，星敏理想坐標系與載體坐標系方向相同；星敏實際坐標系為O-Xc′Yc′Zc′。假設星敏與慣導剛性固連，即不考慮撓曲變形，則c′系相對c系有3個小角度的安裝誤差角：αX、αY、αZ，則c系可通過繞Y、Z、X軸3次轉動與c′系重合，因此c系與c′系之間的轉換矩陣可表示為

(1)

慣性坐標系(i)與地球坐標系(e)可以通過格林尼治恒星時(Greenwich Sidereal Time，GST)聯系起來，即

(2)

導航坐標系選擇北天東地理坐標系(n)，n系與e系的轉換關系，需要使用當地的經度(λ)和緯度(φ)，即

(3)

由慣導提供的經度(λc)和緯度(φc)所確定的坐標系為計算地理坐標系(nc)，設慣導經緯度與真實經緯度僅存在小角度誤差：δλ、δφ，于是nc系與n系的轉換關系可表達為

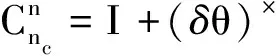
(4)

依靠慣導輸出姿態確定的地理坐標系(np)相對真實的地理坐標系(n)有3個誤差角：φN、φU和φE。由于這3個角均為小量，故np系與n系的轉換關系可以表達為

(5)

2 慣性/星光組合導航方案

在現代姿態匹配方法中，通常利用主、子慣導姿態陣的乘積來構造觀測量[8]。借鑒這種思想，將天文導航提供的姿態矩陣作為主慣導的姿態陣，而慣導系統實時解算的姿態矩陣作為子慣導的姿態陣。本文設計的慣性/星光組合方案如圖1所示。

圖1 慣性/星光組合導航方案Fig.1 SINS/CNS integrated navigation scheme

星敏可輸出星敏坐標系相對慣性參考坐標系的3個歐拉角或者姿態矩陣。輸出中包含安裝誤差角，則有

(6)

慣導輸出的姿態矩陣為

(7)

2個姿態陣不在同一個參考系下，故不能直接用于匹配。可以將慣導輸出轉換至慣性坐標系下，也可將星敏輸出轉換至地理坐標系中。兩種辦法實質一樣，本文采取前者

(8)

GST=ωieΔt

(9)

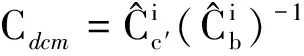
(10)

(11)

由式(10)、式(11)可知，觀測量中包含三種誤差源：慣導的姿態誤差、慣導的位置誤差和星敏感器的安裝誤差。由于三種誤差權重相當，給誤差分離帶來了困難。在地面標定的過程中，位置誤差較小，觀測量中可只考慮姿態誤差與安裝誤差的貢獻。

對于狀態變量，考慮慣導的位置誤差、速度誤差、失準角、陀螺漂移以及星敏的安裝。由于單獨的姿態匹配算法無法估計加表零位，因此可不予考慮狀態變量，將其計入未建模誤差。因此，慣性/星光組合導航系統的狀態變量為

(12)

位置誤差方程為

(13)

速度誤差方程為

(14)

φNfE-φEfN

(15)

φUfN-φNfU

(16)

姿態誤差方程為

(17)

(18)

(19)

量測方程為

Zdcm=Hx+w

(20)

其中

(21)

以上，建立了慣性/星光組合導航系統的卡爾曼濾波模型。

3 仿真分析

為驗證算法的有效性，本文設計了兩種不同的載體軌跡，并進行數學仿真，如表1所示。

表1 兩種不同的載體軌跡

初始誤差：初始水平失準角為0.01°，方位失準角為0.05°；初始經緯度誤差為5m，高度誤差為1m。星敏三軸安裝誤差均為60″。

軌跡總時長為1200s，星敏在150s以后開始工作。濾波周期與星敏姿態輸出周期相同，均設置成1s。限于篇幅，以下僅給出某一次蒙特卡羅仿真結果。

由圖2和圖3易見，在載體無姿態機動的條件下，濾波器對星敏安裝誤差角的估計作用并不強，也無法對初始姿態誤差進行估計。由圖4可以看出，這種情況下，陀螺漂移的估計效果也不理想。

由圖5可以看出，當載體進行滾轉機動以后，星敏y方向與z方向的安裝誤差能快速估計出來，并且快速收斂。由圖6易見，直到載體進行航向機動，x方向的安裝誤差才得以估計出來。另外結合圖5、圖6、圖7可以發現，失準角與安裝誤差角存在耦合關系：只有當安裝誤差角估計出來，對應軸向上的失準角才能得以估計。對比圖4和圖8，情形二對于陀螺漂移的估計作用優于情形一。

對于情形二，進行20次蒙特卡羅仿真，星敏三軸安裝誤差角標定精度(σ)如表2所示。