永磁同步電機電流調節器性能研究
杜玉亮
(1 中國鐵道科學研究院集團有限公司 機車車輛研究所, 北京 100081;2 北京縱橫機電科技有限公司, 北京 100094)
隨著軌道交通行業的發展,高速動車組列車電傳動系統輕量化、高效能已成為路內技術研究的重要方向[1]。與目前我國動車組列車普遍采用的異步電機不同,永磁同步電機(Permanent Magnet Synchronous Motor, PMSM)轉子為永磁體結構,它無需轉子勵磁電流,因而功率密度和電機效率更高[2]。永磁牽引技術在軌道交通領域彰顯出強大的活力,阿爾斯通、西門子、東芝、中車株洲所等國內外軌道交通裝備供應商均已完成永磁同步電機在軌道交通裝備上的開發應用和裝車運行。
電流調節器作為永磁同步電機矢量控制的內環,其動態性能和魯棒性直接影響永磁同步電機控制性能[2-3,5]。矢量控制中,通過坐標變換將電機定子三相電流轉換為同步旋轉坐標系(Synchronous Rotating Frame, SRF)dq軸下直流量進行控制,但靜止坐標系到同步旋轉坐標系轉換后,電機定子dq軸之間存在交叉耦合,隨著電機轉速的升高會影響電流內環的動態性能[3,6-7]。
文中推導了永磁同步電機復矢量數學模型,基于該模型對同步旋轉坐標系前饋/反饋解耦PI電流調節器和同步旋轉坐標系復矢量電流調節器的控制器性能做了對比分析。理論分析和仿真結果驗證了同步旋轉坐標系復矢量電流調節器優異的動態性能。
1 永磁同步電機復矢量數學模型[4]
定義復矢量變量
(1)
永磁同步電機在靜止坐標系下的復矢量數學模型如式(2),式中上標“s”表示靜止坐標系
(2)

(3)
復矢量變量由靜止坐標系轉換為同步旋轉坐標系時有
(4)
上標“r”表示同步旋轉坐標系。由式(4)可知,微分運算轉為同步選坐標系如式(5)
(5)
其中p代表微分算子,將式(4)式(5)代入式(3)可得同步旋轉坐標系下定子電壓矢量方程
(6)
化簡后可得同步旋轉坐標系永磁同步電機定子電壓復矢量方程
(7)
式中
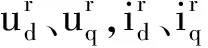
由式(7)可以得到永磁同步電機d軸和q軸電壓方程矩陣為
(8)
2 永磁同步電機電流調節器動態性能分析[3]
采用復矢量描述永磁同步電機模型可以簡化分析,永磁同步電機數學模型由多輸入多輸出系統變換為單輸入單輸出系統。由式(7)可以得到永磁同步電機復矢量模型為
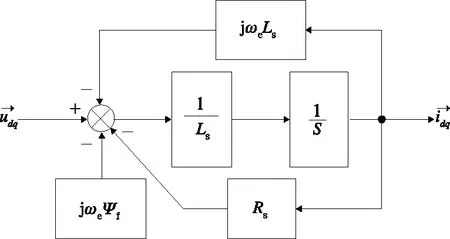
圖1 永磁同步電機復矢量數學模型
圖1 中永磁磁鏈產生的反電動勢項jωeψf可以作為一個常量,假設不考慮其影響,則永磁同步電機復矢量數學模型在同步旋轉坐標系下傳遞函數如式(9)
(9)
式(9)可以看出PMSM模型中包含一項與同步角頻率相關的耦合項jωeLs。隨著電機轉速的升高,dq軸交叉耦合項jωeLs隨同步頻率增大而增大。因此dq軸交叉耦合項的解耦處理是永磁同步電機控制的關鍵,直接影響中高速段電機控制性能。
2.1 基于狀態反饋解耦的同步旋轉坐標系PI電流調節器
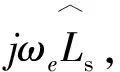

圖2 狀態反饋解耦的同步旋轉坐標系PI電流調節器控制框圖
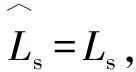
由圖2可推導狀態反饋解耦系統閉合傳遞函數如式(10)
(10)
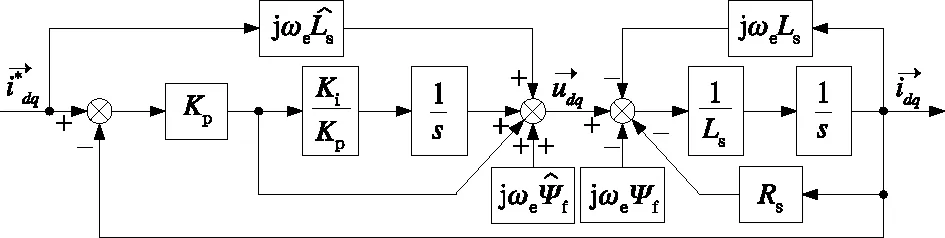
圖3 基于前饋解耦的同步旋轉坐標系PI電流調節器控制框圖
根據圖3可知,基于前饋解耦的同步旋轉坐標系PI電流調節器閉環傳遞函數為
(11)
圖4是永磁同步電機同步頻率從0到100 Hz變化時,基于前饋解耦的PI電流調節器系統閉環零極點變化情況。
基于前饋解耦同步旋轉PI電流調節器零點Z1軌跡如圖4中所示,零點Z1軌跡試圖抵消變化的主導極點P1。由此可知,基于前饋解耦同步旋轉PI電流調節器的本質是通過改變系統零點位置以抵消耦合項的影響,但其傳遞函數中仍存在耦合項,耦合未完全抵消,隨著同步頻率的升高,主導極點P1向虛軸移動表明系統仍有不穩定趨勢。
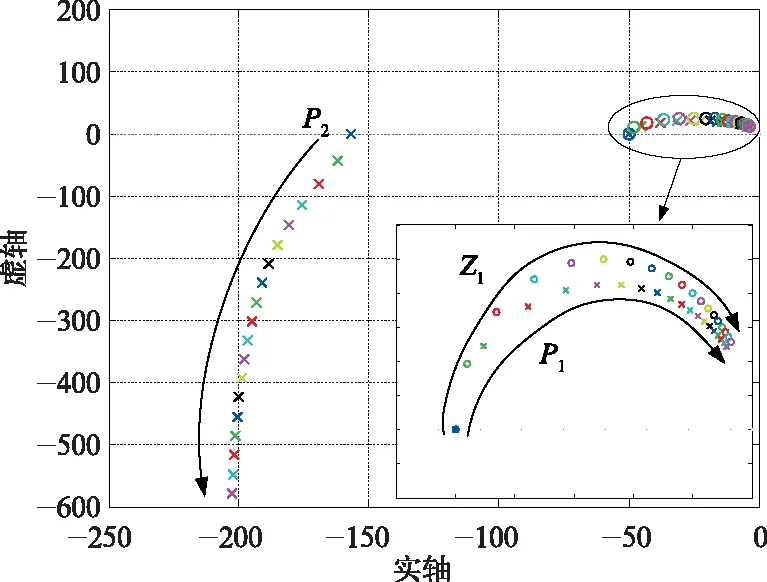
圖4 基于前饋解耦的同步旋轉坐標系PI電流調節器零極點分布圖

圖5 基于前饋解耦同步旋轉坐標系PI電流調節器波特圖
圖5給出了前饋解耦方法的波特圖,當系統同步頻率fe增大時,如圖中fe=50 Hz、fe=100 Hz,系統幅頻特性和相頻特性均與零速時幅頻特性和相頻特性有所差異。
2.2 同步旋轉坐標系復矢量電流調節器
改善電流調節器性能、消除耦合項影響的另一種方法是:不改變被控對象極點位置,對電流調節器進行改進,使電流調節器產生與被控對象極點位置相同的復零點,以滿足零極點對消條件達到消除耦合的目的。
同步旋轉坐標系復矢量電流調節器控制結構如圖6所示。
根據圖6可知,基于復矢量電流調節器系統閉環傳遞函數為式(12)
(12)
復矢量電流調節器的核心是改變PI電流調節器的結構,將PI調節器的零點由-Ki/Kp移至-Ki/Kp-jωe,這樣系統零點與主導極點能時刻相抵消。此外,復矢量電流調節器只需要控制器滿足Ki/Kp=Rs/Ls即可實現解耦控制,與電機電感Ls無關,因此復矢量電流調節器對電機參數的依賴程度遠低于前饋解耦方法。

圖6 基于同步旋轉坐標系復矢量電流調節器控制框圖
圖7是永磁同步電機同步頻率從0到100 Hz變化時,同步旋轉坐標系復矢量電流調節器系統閉環零極點變化情況。由于在電機任何同步頻率處,復矢量電流調節器均能實現其主導極點與零點相抵消,如圖中P1、Z1所示,因此系統整定為典型I型系統。同樣地,同步旋轉坐標系復矢量電流調節器波特圖也可以在任意同步頻率處均具有理想的帶寬,這里不再給出。
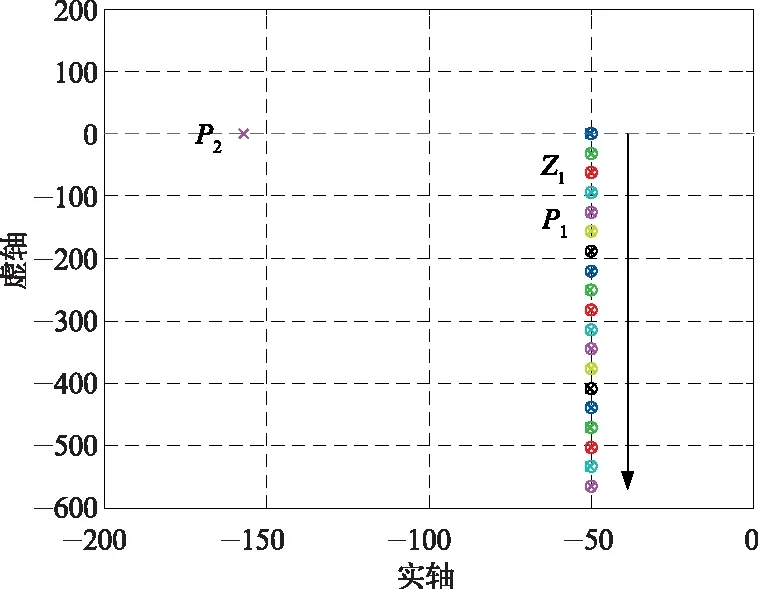
圖7 基于復矢量電流調節器零極點分布圖
2.3 兩種電流調節器對比
基于反饋解耦電流調節器和復矢量電流調節器是兩種行之有效的控制方法,兩者本質上是一致的,都是試圖改造系統主導極點或控制器零點位置,以實現主導極點和零點相互抵消。下面從兩方面對這兩種電流調節器進行比較。
(1)對電機參數依賴性
基于反饋解耦電流調節器系統閉環傳遞函數如式(13)
(13)
可以看出當電機參數估算準確時,系統是典型I型系統。


圖8 電機參數估算差異下反饋解耦電流調節器波特圖(fe=100 Hz)
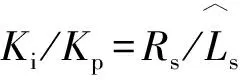
當電機參數估算準確時,復矢量電流調節器可以取得良好的帶寬性能。當參數估算不準確時,如圖8中綠線和藍線所示,復矢量電流調節器性能受到一定影響,但與紅線相比差異非常小。此外,復矢量電流調節器相比反饋解耦PI電流調節器具有更好的電機參數魯棒性,其對電機參數依賴性更小,展示出更強的抗干擾性能。
(2)交叉耦合程度
電機電流調節器除了要具備更弱的電機參數依賴性,還應對電機交叉耦合項實現良好的解耦效果。上面分析可知,電機交叉耦合程度與同步頻率密切相關,一般來說隨著同步頻率的升高較差耦合程度愈強。
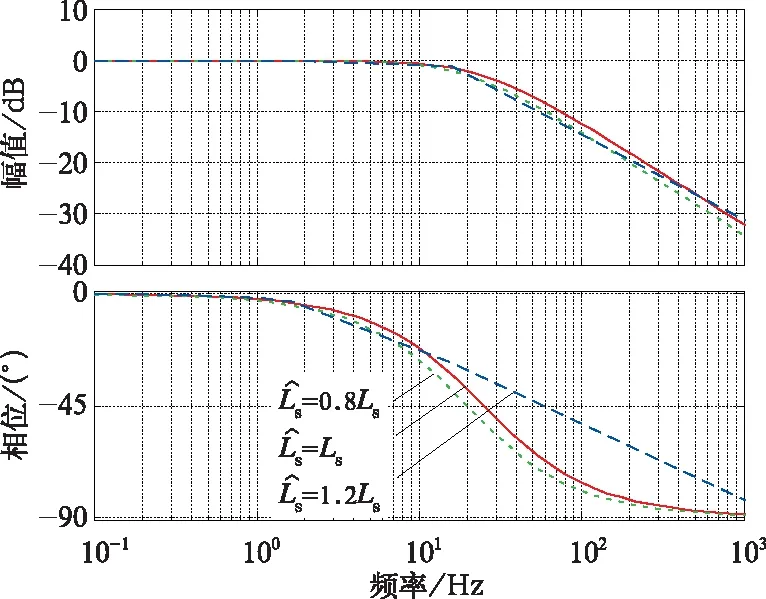
圖9 電機參數估算差異下復矢量電流調節器波特圖(fe=100 Hz)
系統閉環傳遞函數均可寫為式(14)形式
(14)
理想情況下,|Gclo(s)|=1,表明系統電流實際值與指令值可實現零靜差跟蹤。實際中,系統交叉耦合是由坐標變換復數因子j引來的,因此在系統閉環傳遞函數中,虛部Im{Gclo(s)}反映了系統交叉耦合的程度。由此可以定義式(15)表達式,觀測其幅頻特性曲線,幅值越大則表明交叉耦合頻率響應的耦合越大。
(15)
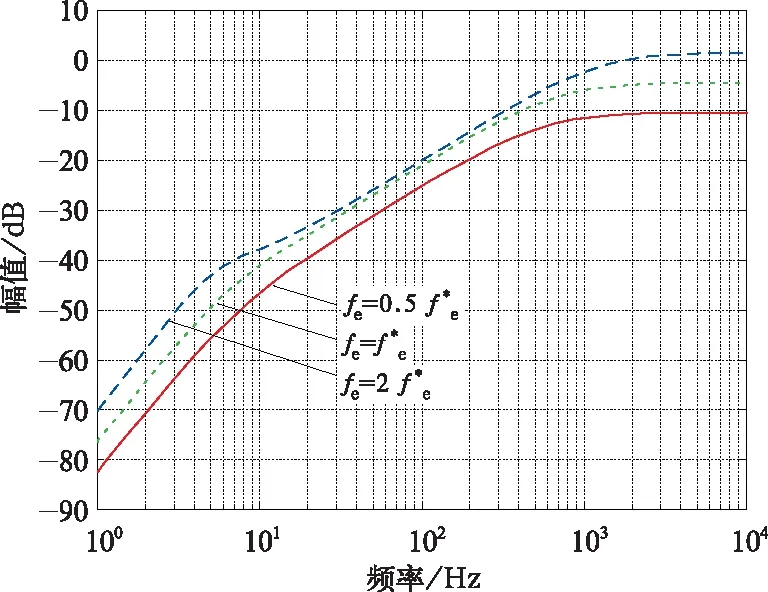
圖10 前饋解耦PI電流調節器交叉耦合響應(f*e=300 Hz)
圖10給出了前饋解耦PI電流調節器交叉耦合響應圖,可以看出隨著電機同步頻率fe增加,交叉耦合響應的幅值也隨之增加,這說明交叉耦合響應加重。由此可得,對于前饋解耦PI電流調節器,同步頻率越大耦合含量越高。
相反地,復矢量電流調節器能夠實現系統主導極點和零點完全抵消,不隨同步頻率的改變而受到影響。因此復矢量電流調節器能夠實現在任意頻率處的完全解耦控制。
3 仿真驗證
分別選擇低速2 000 r/min和高速12 000 r/min兩種情況進行仿真。在每種情況下,分別改變d軸和q軸電流指令值,觀察另一電流變化情況。d軸電流指令值在0.3 s由-10 A階躍至-30 A,q軸電流指令值在0.2 s 由10 A階躍至30 A。系統帶寬頻率設計為2 000 Hz。
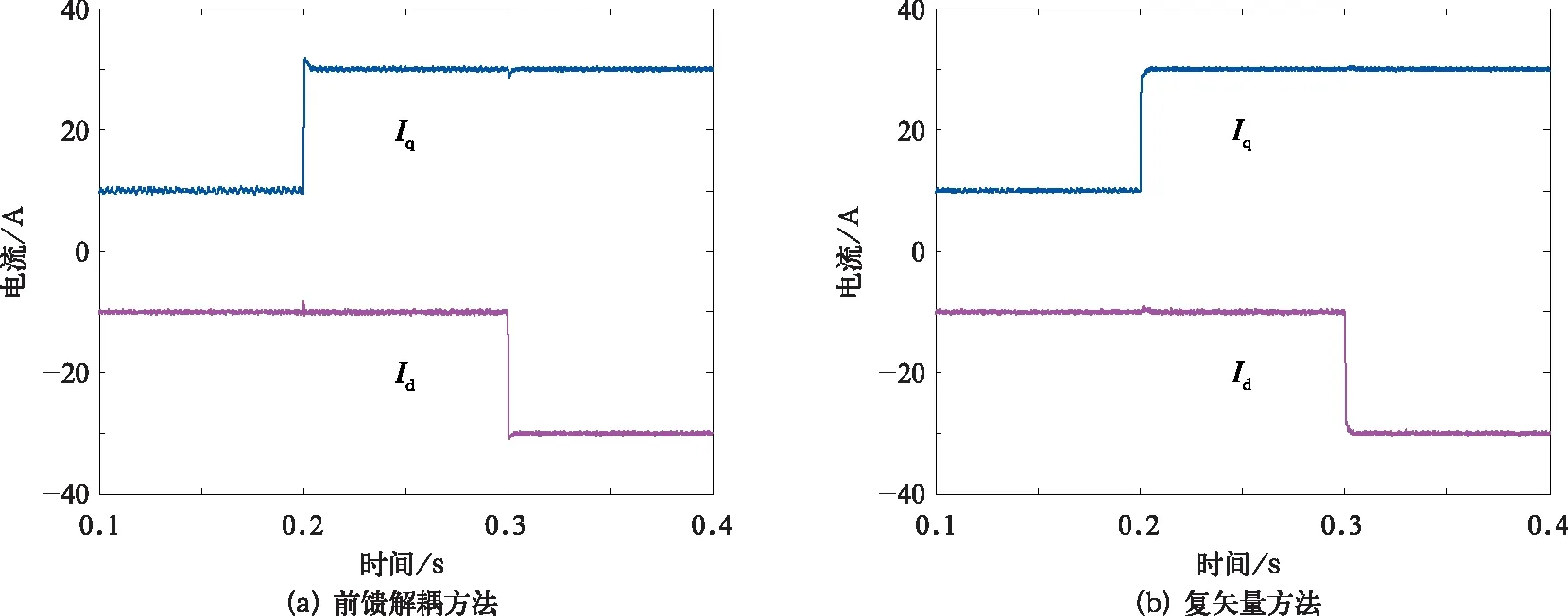
圖11 2 000 r/min時兩種方法動態特性仿真波形

圖12 12 000 r/min時兩種方法動態特性仿真波形
(1)2 000 r/min轉速
圖11給出了電機運行在2 000 r/min時前饋解耦PI電流調節器和復矢量電流調節器動態特性仿真波形圖。0.2 s時,Iq電流由10 A階躍至30 A,可以看出前饋解耦方法Id電流有微小波動,復矢量方法基本無波動;0.3 s時,Id電流由-10 A階躍至-30 A,前饋解耦方法Iq電流也出現微小波動,復矢量方法也基本無波動。前饋解耦方法在低速時解耦性能雖與復矢量方法相比略有劣勢,但解耦效果仍然比較理想。
(2)12 000 r/min轉速
電機運行于12 000 r/min時,從仿真結果可以看出前饋解耦方法和復矢量方法的解耦效果有了明顯的差異。在0.2 s時Iq電流由10 A階躍至30 A時,Id電流隨之產生較大的振蕩,幅值達到10 A左右;0.3 s時Id電流由-10 A階躍至-30 A時,Iq電流同樣有較大的振蕩,幅值達到5 A左右。這與上面分析一致,前饋解耦PI電流調節器特性隨著電機同步頻率的升高而逐漸惡化。然而復矢量電流調節器在12 000 r/min時,Id、Iq電流也能實現與低速時一樣的良好解耦效果。
仿真結果證明了上面對前饋解耦方法和復矢量方法的理論分析,表明前饋解耦方法動態特性隨著電機同步頻率的升高而逐漸惡化,復矢量方法在任何同步頻率處均有理想的動態特性。
4 結 論
文中推導了永磁同步電機復矢量數學模型,對比分析了同步旋轉坐標系前饋/反饋解耦PI電流調節器和同步旋轉坐標系復矢量電流調節器的控制器性能
(1) 同步旋轉坐標系前饋/反饋解耦PI電流調節器在低速時解耦效果較好,但隨著電機轉速的升高,該控制器對電機參數的依賴性增強,解耦效果下降。
(2) 同步旋轉坐標系復矢量電流調節器在任何同步頻率處均有理想的解耦效果和動態特性,且對電機參數的依賴性更低。優于傳統電流控制方法,為永磁同步電機控制提供了一種抗擾能力強、動態響應迅速的控制方法。

