基于關鍵字密度的XML關鍵字檢索*

覃遵躍,湯 庸,徐洪智,黃 云

1(中山大學 數據科學與計算機學院,廣東 廣州 510006)

2(吉首大學 軟件學院,湖南 張家界 427000)

3(華南師范大學 計算機學院,廣東 廣州 510631)

1 引 言

XML是互聯網中信息表示和交換的事實標準,在電子政務、電子商務、金融、出版、科學數據和各種資源數字化等方面扮演著極其重要的角色.利用關鍵字檢索 XML數據,用戶不需要學習復雜的查詢語言,并且也無需預先了解XML數據的結構知識,因此研究XML關鍵字檢索是非常迫切和必要的.

XML關鍵字檢索只需要返回XML樹片段,該樹片段包含了匹配的所有關鍵字[1,2].文獻[3-8]詳細介紹了返回 XML樹片段的檢索方式,通常,這種檢索方式的結果包含了每個關鍵字實例的一棵最小連通樹,該樹的根節點是包含了所有關鍵字實例的最低公共祖先LCA(lowest common ancestor).LCA是針對XML關鍵字檢索的所有可能情況,有些LCA可能不符合用戶的查詢意圖.為了返回與用戶意圖密切的LCA,文獻[9-13]采用過濾方法拋棄了與用戶意圖不相關的 LCA,但這些方法經常過濾掉了用戶想要的 LCA,具有低的準確率和召回率[14].針對過濾語義不足的問題,文獻[6,15,16]設計了Top-k算法,對查詢結果LCA進行排名并優先選擇Top-K個結果.對于XML數據進行關鍵字檢索也可以通過TF*IDF和PageRank進行排名[1,9,14,17]以提高用戶的檢索興趣.

雖然對 XML關鍵字檢索研究取得了很多研究成果,但仍然存在一些問題.首先是檢索質量問題,例如通過過濾語義SLCA[11,18,19]和ELCA[13,20]來產生LCA子集,然后對子集進行排名,這種方法存在丟失相關查詢結果的問題.第二是查詢效率問題,在檢索關鍵字較多時將返回大量的LCA結果,處理LCA排名主要基于關鍵字倒排表的規模[8,14],因此,當數據集規模增大時,算法不能很好地滿足應用要求.文獻[21]提出了一種通用的自上而下(top-down)的處理策略來發現 LCA/SLCA/ELCA 語義的共同祖先重復(CAR)和訪問無用節點(VUN)問題,但不能對LCA節點進行排名.

針對上面存在的兩個問題,本文提出了對LCA直接進行排名的TopLCA-K方法,該方法綜合考慮了查詢關鍵字數量、邊的構成和路徑等情況,然后計算出每個LCA的大小.

本文主要貢獻包括:

(1) 提出了LCA與用戶查詢意圖相關的兩個規則.用戶查詢意圖與查詢關鍵字實例到LCA邊的數量成反比,以及用戶查詢意圖與LCA子樹路徑的數量成反比.

(2) 建立了計算LCA分數的公式.根據前面提出的兩個規則,利用邊密度和路徑密度作為衡量LCA值的方法.

(3) 設計了計算LCA值的算法TopLCA-K.為了避免丟失部分滿足用戶需要的查詢結果,提出對所有LCA進行打分.為了提高查詢效率,提出了中心位置索引CI.根據LCA分數進行排名,把最可能滿足用戶查詢意圖的LCA首先展示給用戶.

(4) 利用實際的不同規模數據集對提出的算法進行了測試,實驗驗證了在查詢關鍵字個數不同的情況下,本文提出的算法具有更高的準確率和召回率,并且返回的K個結果更符合用戶需要.

本文第2節介紹研究背景和相關工作.第3節介紹度量LCA大小的概念和方法以及TopLCA-K算法.第4節顯示本文提出的算法的實驗結果,以及與其他方法的比較情況.第 5節總結本文的工作,并給出未來的研究方向.

2 研究背景與相關概念

2.1 研究背景

因為XML半結構化數據不像關系數據庫那樣具有嚴格的模式,因此對這種類型的數據進行關鍵字檢索是一項復雜的任務.很多文獻針對XML關鍵字檢索提出了各種類型的查詢語義,可以分為基于樹模型和基于圖模型的查詢語義.在基于樹模型的關鍵字查詢語義中,LCA 是所有其他語義的基礎,其中,SLCA[11]、ELCA[1,13]、MLCA[10]、XSearch[9]、VLCA[12]、TLCA[22]等是基于 LCA 的代表性語義.基于圖模型的查詢語義主要借鑒關系數據庫的關鍵字查詢思想[23],即對于給定的一組查詢關鍵字,返回CN(connected network).

SLCA[11]過濾掉了后裔LCA；在ELCA[1,13]語義定義中,v是一個LCA節點,如果以v為根的子樹中過濾掉所有其他以LCA節點為根的子樹后,v仍然包含所有關鍵字,則v是一個ELCA節點；MLCA[10]語義去掉包含了關鍵字標簽相同但路徑不同的LCA；VLCA[12]和XSearch[9]在LCA的基礎上,將不同關鍵字到LCA路徑上存在的同名節點的結果排除在外.基于樹模型的查詢語義除了LCA之外,還有MCT(minimal cost tree)語義[15].

基于圖模型的查詢語義把 XML數據建模為一個圖,返回 CN(connected network)[24]作為關鍵字查詢結果.每個CN都是文檔樹D的一個無環子圖T,并且T包含查詢Q中的所有關鍵字至少1次,而T的任何真子圖都不包含Q中的所有關鍵字.基于CN的一種典型查詢語義是MCN(meaning connected network)[19],該查詢語義找出給定關鍵字之間有意義的關系.XKeyword[24]和BLINKs[25]也是基于圖的查詢語義.

已經提出的針對XML關鍵字查詢語義,或者基于LCA進行過濾,例如SLCA、ELCA等,或者基于CN進行過濾,例如 MCN.雖然這些過濾語義可以返回更加貼近用戶意圖的查詢結果,但用戶查詢往往很復雜,因此這些過濾的查詢語義也顯示出了低召回率問題[14].為了彌補過濾查詢語義存在低召回率問題,對符合條件的查詢結果進行排名是一種有效的解決辦法.對查詢結果進行排名,可以把與用戶查詢意圖更相關的查詢結果放在前面.已有排名方法分為兩種,一種是根據 XML結構和語義上的相關性進行排名[1,6,9,14,15,26,27],另一種是按照某種統計度量辦法對LCA節點進行評分排名[1,6,9,14,15,28-30].例如XRank[1]對PageRank算法進行了改進而適用于XML關鍵字查詢結果排名；XSearch[9]對 TF*IDF函數進行改進使之適用于 XML文檔樹結構的關鍵字查詢排名；XReal[4]的排序思想基于TF*IDF,考慮的排序因素包括關鍵字頻率、關鍵字出現順序、關鍵字在查詢結果中的位置以及結果的大小等.Termehchy和 Winslett[14]通過采用交互信息來計算結果相干性以進行排名；Nguyen和 Cao[31]使用交互信息來比較結果,然后在查詢結果之間定義了一個支配關系來進行排名；SAIL[15]定義了最小代價樹,并且通過使用鏈接來分析關鍵字對之間的相關性,最后返回Top-k查詢結果；XBridge[28]在使用打分函數時考慮了查詢結果的結構,然后對查詢結果進行分類；文獻[25]基于圖模型數據,提出了一種結合結構大小、PageRank以及TF*IDF這3種排序思想的混合排名機制.文獻[26]提出了一個新的對XML數據的關鍵字查詢進行排名和過濾語義的方法XReason語義,該方法基于模式推理,模式記錄了查詢匹配的結構和語義特征.為了利用模式進行推理,提出了模式之間的同態關系.該方法的優點是從整體的角度考慮查詢匹配,避免了以前語義利用局部XML子樹比較查詢匹配存在的缺陷.

2.2 相關概念

一般情況下,把XML文檔建模為一棵有序標簽樹,樹中的節點代表XML元素或者屬性,每個節點有一個id號(節點唯一的編號)、一個標簽(元素或者屬性),有的節點是一個值(對應元素文本值或者屬性值).

定義1(XML有向樹).一個XML文檔建模為一棵帶標簽的有向樹T(V,E,r),其中,V表示節點的集合,E表示邊的集合,r是樹的根節點.

定義2(關鍵字匹配集合KMS).對給定的XML有向樹T(V,E,r)和查詢關鍵字k,用KMS(k)表示T中所有與關鍵字k匹配的節點集合,KMS(k)={v|v∈V,k=tag(v)或者k=value(v)}.其中,tag(v)表示節點v的標簽,value(v)表示節點v的值.

例如圖1中,KMS(A)={4,10,15},KMS(B)={6,11,16},KMS(C)={8,12,17}.

定義3(節點集N的最低公共祖先LCA(lowest common ancestor)).給定XML有向樹T(V,E,r)和m個元素節點集N={vi|vi∈V,1≤i≤m},節點v=LCA(N)當且僅當滿足以下條件:

(1) 任意的vi∈N,v是vi的祖先節點,v∈V,1≤i≤m.

(2) 不存在節點u(∈V),u是v的后裔,并且u是任意vi(∈N)的祖先節點.

定義4(LCA集合LCASet(T,Q)).針對XML有向樹T(V,E,r)的關鍵字查詢Q={k1,k2,…,km},LCA集合LCASet(T,Q)={v|v∈V且v=LCA(k[1,i],k[2,i],...,k[m,i])},k[1,i]∈KMS(k1),k[2,i]∈KMS(k2),…,k[m,i]∈KMS(km).

例如圖 1中,查詢Q={A,B,C},LCASet(T,Q)={1,2,9,14},因為節點 1=LCA({4,11,17})(其中的一種情況),節點2=LCA({4,6,8}),節點9=LCA({10,11,12}).

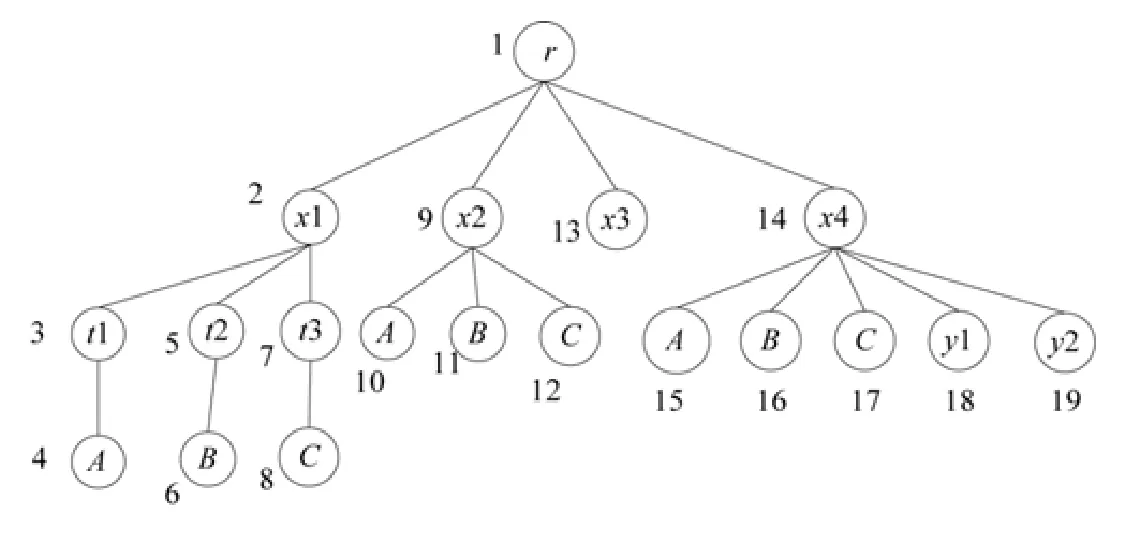
Fig.1 Ordered XML document tree圖1 有序XML文檔樹

3 相關定義

3.1 研究動機

圖2表示某圖書館的藏書情況,是一棵XML有序標簽樹T,圓角矩形中的數字表示節點的Dewey編碼,旁邊是節點的標簽,葉子節點下的字符串表示值,例如tag(1)=booklist,tag(1.2)=book,value(1.3.1.1)=BigDataSystem.

考慮對該樹的關鍵字查詢Q={BigData,Felix,James},檢索目標是查詢書名包含 BigData,作者名字中包含Felix或者 James的圖書.這些關鍵字在樹中出現多次,例如 1.1.3.1.1.1、1.2.1.1、1.2.4.1.1.1、1.3.1.1和 1.4.1.1這5個節點中出現關鍵字BigData.按照LCA的定義,有LCASet(T,Q)={1,1.1,1.1.3,1.2,1.2.4.1,1.3,1.4}這7個節點滿足查詢Q的要求,這些LCA中,只有1.2、1.3、1.4和1.2.4.1滿足用戶查詢要求；1和1.1.3是連接節點,因此不符合查詢要求；1.1標簽包含Felix和James,但與title對應的書是XML,而不是BigData,因此1.1雖然是書但也不符合用戶查詢意圖.按照已經提出的過濾語義,例如根據SLCA語義則不能返回 1.2而是返回1.2.4.1,按照MLCA語義則不能返回1.3,而根據ELCA語義返回1.1.3節點也有意義,這些過濾語義并不能準確地表達用戶的查詢意圖.

上述查詢語義失敗的原因是因為那些過濾語義沒有充分考慮現實應用的復雜性,直接刪除了某些 LCA,導致了低召回率和準確率.

針對已經出現的問題,下面提出了按照查詢關鍵字數量、關鍵字實例路徑、LCA類型以及關鍵字實例離散度等綜合因素對LCA進行度量的新方法,然后按照LCA測量值的大小返回Top-K個結果.

Fig.2 XML for library圖2 圖書館藏書XML文檔

3.2 LCA與用戶意圖相關性規則

規則1.用戶查詢意圖與查詢關鍵字實例到LCA節點邊的數量成反比.

在 LCA子樹中,查詢關鍵字實例離 LCA節點越近,表示 LCA越接近用戶的查詢意圖,查詢關鍵字實例到LCA節點邊的數量表示了它們之間的距離.

如圖1所示,關鍵字查詢Q={A,B,C},x1和x2節點都是查詢Q的LCA,顯然,查詢關鍵字的實例距離x2比x1更近,因此,x2比x1更符合用戶的查詢意圖.

該規則確定了查詢關鍵字實例與LCA之間的縱向關系.但在實際情況中,除了縱向關系之外還存在橫向關系,即查詢關鍵字實例在整個LCA子樹中的占比情況.如圖1所示,x2和x4都是查詢Q的LCA,根據規則1,它們的度量值是相同的,但x2僅僅包含了3個查詢關鍵字實例,而x4包含了y1和y2兩個冗余節點,因此,x2比x4更符合用戶查詢需求.針對這個問題,提出了規則2.

規則2.用戶查詢意圖與LCA子樹路徑的數量成反比.

規則2反映了LCA中查詢關鍵字實例的離散度,LCA包含的子樹相對于查詢關鍵字越多,表示查詢關鍵字之間的離散度越大,說明該LCA與用戶查詢的相關度越小.

3.3 基于關鍵字密度的LCA評分方法

根據規則1和規則2,給出了計算LCA排名的有關定義,并利用這些定義建立了計算LCA分數的公式.

定義5(最小最優LCA路徑數MOPSize(Q)).對于XML有向樹T(V,E,r)的關鍵字查詢Q={k1,k2,…,km},與查詢Q對應的LCA集合LCASet(T,Q),則最小最優LCA的路徑數是關鍵字的數量,即MOPSize(Q)=|Q|.

對于關鍵字查詢Q,LCA包含了所有查詢關鍵字實例,最小最優情況是LCA節點到葉子節點的每條路徑上包含一個查詢關鍵字實例.這種情況在橫向軸上沒有冗余信息,也不缺少信息.如果 LCA節點到葉子節點的路徑數多于關鍵字數量,則說明LCA有多余信息,這種多余信息可能會對用戶產生干擾.例如圖2中,節點1.4是關鍵字查詢Q={BigData,Felix,James}的LCA,MOPSize(T,Q)=3,因為3個葉子節點到LCA的路徑剛好包含了3個查詢關鍵字；雖然節點1.3也是查詢Q的LCA,但它的子樹有5條葉子到LCA的路徑,說明包含了冗余信息.

定義 6(關鍵字與 LCA的聯系度 CSize(T,Q,u,v)).對于 XML有向樹T(V,E,r)的關鍵字查詢Q={k1,k2,…,km},u∈LCASet(T,Q),v∈KMS(ki)(1≤i≤m),存在一條從u到v的路徑p(u,t1,t2,…,tn,v),CSize(T,Q,u,v)=路徑p的長度.

定義6表明了LCA與查詢Q的關鍵字實例之間縱向緊密度,CSize越小,表明關鍵字與LCA越密切.如圖2所示,1.1.3和1.3都是關鍵字查詢Q={BigData,Felix,James}的LCA,CSize(T,Q,1.1.3,Felix)=4,表明在1.1.3中,關鍵字Felix與該LCA的距離是4,而CSize(T,Q,1.3,Felix)=3,表明在1.3中,關鍵字Felix與該LCA的距離是3,說明后者比前者更接近用戶需求.

為了對規則1進行計算,提出了LCA邊密度的概念,它表示LCA子樹中查詢關鍵字實例到LCA邊的數目與查詢關鍵字之間的關系.

定義7(邊密度LCAEDen(T,Q,v)).對于XML有向樹T(V,E,r)的關鍵字查詢Q={k1,k2,…,km},某個LCA關鍵字的邊密度為

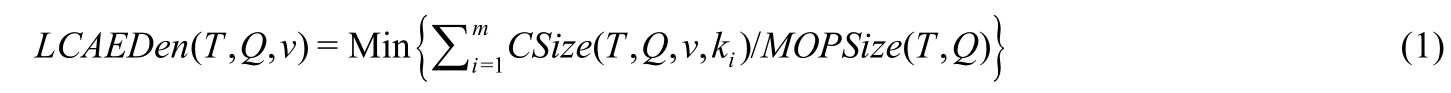
v∈LCASet(T,Q),ki∈Q且是v的后裔,1≤i≤m.

邊密度LCAEDen(T,Q,v)表示查詢關鍵字實例與LCA的縱向聯系緊密度.該值越小,說明查詢關鍵字實例與LCA聯系得越密切,當然,查詢結果就越好.如圖2所示,節點1.4是Q={BigData,Felix,James}的LCA,它的邊密度LCAEDen(T,Q,1.4)=8/3；節點1.1.3也是Q的LCA,它的邊密度是LCAEDen(T,Q,1.1.3)=11/3,因此1.4比1.1.3更符合用戶查詢意圖.但是1.3和1.4都是Q的LCA,它們的邊密度LCAEDen(T,Q,1.4)=LCAEDen(T,Q,1.3)=8/3,但是顯然,1.3比1.4包含了更多的冗余信息,因此1.3沒有1.4好.

針對邊密度相同而LCA存在冗余信息的情況,根據規則2,提出了路徑密度這一概念.它表示LCA子樹中查詢關鍵字實例在整個LCA路徑中的關系,即查詢關鍵字的橫向關系.

定義 8(LCA的實際路徑數量 RPSize(T,Q,u)).對于 XML有向樹T(V,E,r)的關鍵字查詢Q={k1,k2,…,km},u∈LCASet(T,Q),RPSize(T,Q,u)=等于u的葉子節點數量.

定義8表明了對于關鍵字查詢Q,從LCA到葉子節點的路徑數量.如圖2所示,節點1.4是關鍵字查詢Q={BigData,Felix,James}的一個 LCA,RPSize(T,Q,1.4)=3,說明該 LCA無冗余信息,而RPSize(T,Q,1.3)=5,說明節點1.3存在冗余信息.

定義9(路徑密度LCAPDen(T,Q,v)).對于XML有向樹T(V,E,r)的關鍵字查詢Q={k1,k2,…,km},某個LCA節點的路徑密度LCAPDen(T,Q,v)=RPSize(T,Q,v)/MOPSize(Q),其中,v∈LCASet(T,Q).

路徑密度LCAPDen(T,Q,v)表示了在整個 LCA子樹中,查詢關鍵字實例路徑存在的稀疏度.該值越大,表示越稀疏,說明該LCA中的冗余信息越多,可能更不符合用戶的查詢意圖.如圖2所示,節點1.4是Q={BigData,Felix,James}的LCA,它的路徑密度LCAPDen(T,Q,1.4)=3/3；節點1.3也是Q的LCA,它的路徑密度LCAPDen(T,Q,1.3)=5/3,因此1.4比1.3更符合用戶查詢意圖.

定義7和定義9分別從縱向和橫向的角度來考慮LCA與用戶查詢意圖的相關度.但存在另一種情況,如果兩個不同LCA的邊密度和路徑密度都相同,我們如何區別它們?XML文檔節點分為連接節點、實體節點、屬性節點和值節點[32].不同節點的含義不同,連接節點表示不同實體之間或者實體與屬性之間的連接關系,相當于關系數據系統中的連接表,實體節點表示現實世界的對象,相當于關系數據庫系統中的實體關系,屬性節點相當于關系數據庫系統表中的屬性,值相當于屬性的記錄值.在實際查詢中,用戶往往對實體比較感興趣,因此在LCA排名中,實體節點比連接節點、屬性節點和值節點更重要.

LCA節點與用戶查詢意圖的契合度是綜合性的因素,定義7和定義9考慮了LCA節點與查詢關鍵字的縱向和橫向關系,定義10建立了綜合考慮各種情況下的LCA評分公式.

定義 10(LCAValue(T,Q,v)).對于 XML有向樹T(V,E,r)的關鍵字查詢Q={k1,k2,…,km},v∈LCASet(T,Q),LCA的分值為

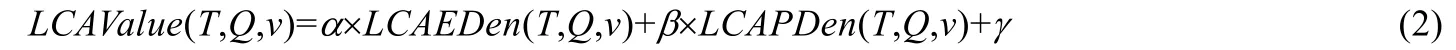
式(2)中,α表示邊密度的權重,β表示路徑密度的權重,γ表示節點類型權重.這里,α和β取值為1.

其中,|LCA|表示LCA的孩子節點個數,t表示與根節點類型相同的節點個數.

在如圖2所示的XML文檔中,對于查詢Q={BigData,Felix,James},計算每個LCA所得分數見表1.

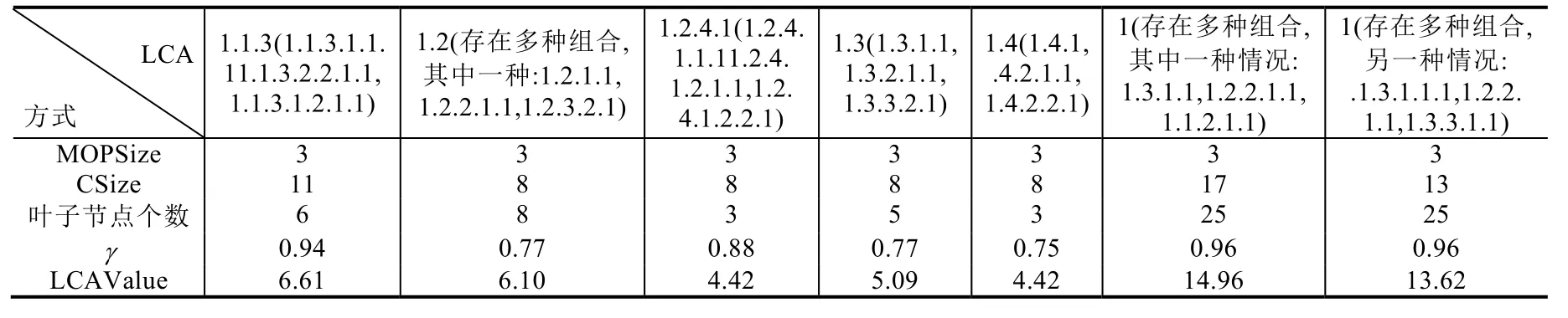
Table 1 LCAValue ofQ corresponding to the XML shown in Fig.2表1 圖2所示XML文檔對應的查詢Q的LCAValue

表1中,查詢Q有3個查詢關鍵字,因此節點1.1.3的MOPSize為3,以1.1.3為根的實際路徑數(葉子節點數)為6,關鍵字BigData、Felix和James與LCA節點1.1.3的聯系度分別為CSize(T,Q,1.1.3,BigData(1.1.3.1.1.1))=3、CSize(T,Q,1.1.3,Felix(1.1.3.2.2.1.1))=4 、CSize(T,Q,1.1.3,James(1.1.3.1.2.1.1))=4,γ=0.94,利 用 公 式 (2)計 算 出LCAValue(T,Q,1.1.3)=6.61；同理,節點1.2也是LCA節點,關鍵字與1.2的聯系度之和為8,葉子節點數是8,利用公式(2)計算出LCAValue(T,Q,1.2)=6.10；同理,LCAValue(T,Q,1.4)=4.42；對于節點 1,存在多種組合情況,表 1列出其中的兩種,第 1種對應的節點為 1.3.1.1(Bigdata),1.2.2.1.1(James),1.1.2.1.1(Felix),它們的LCAValue(T,Q,1)=14.96,而另一種組合的節點為 1.1.3.1.1.1(Bigdata),1.2.2.1.1(James),1.3.3.1.1(Felix),它們的LCAValue(T,Q,1)=13.62.

表1最后一行顯示,最符合用戶查詢意圖的節點1.4和1.2.4.1的LCAValue值最小,節點1.3次之,值較大的節點1表明該節點最不符合用戶查詢意圖.因此,可以按照LCAValue值從小到大排名,把最符合用戶查詢意圖的LCA節點優先返回給用戶.

4 主要算法

4.1 計算LCA分值的算法TopLCA-K

為XML文檔樹中的每個節點賦予一個體現結構關系的Dewey編碼,通過該編碼僅計算公共前綴即可求出任意兩個節點的LCA.如圖2所示,節點1.1.2.1.1和節點1.1.3.2.2.2.1,它們的公共前綴是1.1,因此,節點1.1是這兩個節點的LCA.

為了提高計算LCAValue的效率,對于XML文檔樹T(V,E,r)的關鍵字查詢Q={k1,k2,…,km},為每個查詢關鍵字建立倒排索引,并根據它們的 Dewey編碼從小到大排序,按照匹配集合中實例節點個數從小到大的順序對每個查詢關鍵字進行排序.表2對查詢Q={BigData,Felix,James}建立了倒排索引表,BigData關鍵字實例有5個節點,Felix關鍵字實例有7個節點,James關鍵字實例有6個節點,按照關鍵字實例個數從小到大排序,并且每個查詢關鍵字的 Dewey編碼也根據從小到大的順序排序.此外,還需要為每個非葉子節點建立該子樹包含葉子節點數的索引表,見表3,為1,1.1,1.1.1,1.1.2和1.1.3建立非葉子節點索引表.

Table 2 Inverted index table forQ={BigData,Felix,James}表2 查詢Q={BigData,Felix,James}的倒排索引表

Table 3 Number of leaf nodes in subtree表3 子樹包含的葉子節點數

基于倒排表算法計算LCAValue值的基本思想是利用貪心算法計算所有查詢關鍵字對應節點的各種組合,利用公式(2)計算該組合的LCA值并進行排名,輸出TopLCA-K的查詢結果給用戶.假設有t個查詢關鍵字,則該算法時間復雜度為O(nt),當查詢關鍵字多并且XML文檔規模很大時,該算法效率很低.

4.2 改進的TopLCA-K算法

為了提高TopLCA-K算法效率以適應大規模XML文檔的環境,對TopLCA-K算法進行改進.

定義11(節點集V′的中間路徑MidP(T,V′,u)).XML有向樹T(V,E,r),節點集,節點u到根節點r構成的路徑p(u,p1,p2,…,pn,r)把節點集V?分為左右兩部分子集V?l和V?r,V?l∩V?r=?,V?l∪V?r=V?,MidP(T,V?,u)=p(u,p1,p2,…,pn,r).

定義12(節點集V′中離節點u最近節點Nearest(T,V?,u)).XML有向樹T(V,E,r),節點集,節點u∈V但u?V?.V?中離u最近的節點為Nearest(T,V?,u),計算Nearest(T,V?,u)的過程如下.

(1) 中間路徑MidP(T,V?,u)把V?分為V?l和V?r,V?l∩V?r=?,V?l∪V?r=V?；

(2)V?l中最大 Dewey編碼節點為vl_max,V?r中最小 Dewey編碼節點為vr_min；

(3)LCA(u,vl_max)=x,LCA(u,vr_min)=y；

(4) 如果x是y的祖先,則vr_min為基于u的V?的中心節點,即Nearest(T,V?,u)=vr_min；如果y是x的祖先,則vl_max為基于u的V?的中心節點,即Nearest(T,V?,u)=vl_max；

(5) 如果x和y是同一個節點,則vl_max為基于u的V′的中心節點,即Nearest(T,V?,u)=vl_max.

圖 1中,設V={3,4,5,7,10,11,13,15,16},中間路徑p(12,9,1)把V分為Vl={3,4,5,7,10,11},Vl中最大編碼為 11,Vr={13,15,16},Vr中最小編碼為13,LCA(11,12,)=9,LCA(12,13)=1,根據定義12(4),則有Nearest(T,V,12)=11.

定義 13(中心節點 CenterNode(T,V,u)).XML有向樹T(V,E,r),為T的每個節點根據深度優先賦予一個Dewey 編碼,節點集V?={v1,v2,…,vm}(vi∈V),V?的m個節點按照 Dewey 編碼從小到大排序后,節點u∈V但u?V?,則CenterNode(T,V?,u)=Nearest(T,V?,u).

性質1.XML有向樹T(V,E,r)的m個節點u1,u2,…,um,x=LCA(u1,u2,…,um)；T中的m+1個節點u1,u2,…,um,u?,LCA(u1,u2,…,um,u?)=y,如果u?是x的后裔,則y是x本身,否則y是x的祖先.

性質2.XML有向樹T(V,E,r)的節點x和y,如果y是x的祖先,則y子樹的葉子節點數大于等于x子樹的葉子節點數,即leafNum(T,y)≥leafNum(T,x).

性質 3.XML有向樹T(V,E,r),節點集V?的m個節點按照 Dewey編碼從小到大排序,V?={v1,v2,…,vm}(vi∈V,1≤i≤m),u∈V但u?V?.CenterNode(T,V?,u)=vj(vj∈V?),則leafNum(T,LCA(u,vj))≤leafNum(T,LCA(u,vj?))(vj≠vj?,vj?∈V?).

證明:因為vj=CenterNode(T,V?,u),根據定義 12 和定義 13,則vj?≠vj,LCA(u,vj?)=LCA(u,vj)或者LCA(u,vj?)是LCA(u,vj)的祖先.根據性質 2,leafNum(T,LCA(u,vj?))≥leafNum(T,LCA(u,vj)). □

圖 2中,按照 Dewey編碼從小到大排序后,V?={1.1.2.1.1,1.1.2.2.1,1.1.3.1.1.1,1.1.3.1.2.1.1,1.1.3.2.1.1,1.1.3.2.2.1,1.1.3.2.2.1.1,1.1.3.2.2.2.1},對于節點 Bob(1.1.3.1.1.2.1),V?的中心點CenterNode(T,V?,1.1.3.1.1.2.1)=1.1.3.1.2.1.1,根 據 性 質 3,leafNum(T,LCA(1.1.3.1.1.2.1,1.1.3.1.2.1.1))≤leafNum(T,LCA(1.1.3.1.1.2.1,v))(v∈V?且v≠1.1.3.1.2.1.1).例 如 ,leafNum(T,LCA(1.1.3.1.1.2.1,1.1.3.1.2.1.1))(=2)≤leafNum(T,LCA(1.1.3.1.1.2.1,1.1.3.2.2.1.1))(=6).同理,leafNum(T,LCA(1.1.3.1.1.2.1,1.1.3.1.2.1.1))(=2)≤leafNum(T,LCA(1.1.3.1.1.2.1,1.1.3.1.1.1))(=3).

在TopLCA-K算法中,如何確定K是一個重要問題.如對于圖2中的Q={BigData,Felix,James},KMS(BigData)={1.1.3.1.1.1,1.2.1.1,1.2.4.1.1.1,1.3.1.1,1.4.1.1}共有 5個節點；KMS(Felix)={1.1.2.1.1,1.1.3.1.1.1.1,1.2.3.2.1,1.2.4.1.2.1.1,1.3.2.1.1,1.3.3.1.1,1.4.2.1.1}共有 7個節點；KMS(James)={1.1.2.2.1,1.1.3.2.2.1.1,1.2.2.1.1,1.2.4.1.2.2.1,1.3.3.2.1,1.4.2.2.1},共有6個節點.按照LCA的概念共有5×7×6=210種組合情況,但是滿足用戶查詢意圖的LCA比這個數值要小得多.實際上,真正滿足用戶意圖的LCA的個數由min{|KMS(BigData)|,|KMS(Felix)|,|KMS(James)|}的值確定,即具有最少關鍵字實例的個數就是用戶需要尋找的LCA個數.

規則 3.對于 XML有向樹T(V,E,r)的關鍵字查詢Q={k1,k2,…,km},滿足用戶查詢意圖的 LCA 個數,即LCANum(T,Q)≤min{|KMS(k1)|,|KMS(k2)|,…,|KMS(km)|},ki∈Q,1≤i≤m.

證明:設ki的|KMS(ki)|具有最小值t,則當kj∈{k1,k2,…,ki-1,ki+1,…,km}時,|KMS(kj)|≥t.對于KMS(ki)中的任意查詢實例節點u∈KMS(ki),LCAValue(T,Q,v)的最小值為α,v為包含了u的一個LCA,該LCA是滿足用戶查詢意圖的LCA.由于|KMS(ki)|的值為t,因此這樣的 LCA 不多于t個,即LCANum(T,Q)≤min{|KMS(k1)|,|KMS(k2)|,…,|KMS(km)|}. □

備注:如果多個LVAValue(T,Q,v)的值相同,則看作是同一個LCA.

利用規則 3能夠解決過濾語義,如 SLCA、MLCA 和 ELCA 等查不全的問題.例如,針對圖 2中的查詢Q={BigData,Felix,James},按照SLCA語義,不能返回1.2節點,但是根據規則3,能夠把節點1.2作為滿足查詢意圖的一個節點返回給用戶.

規則3確定了TopLCA-K算法中K的值,利用定義13確定搜索倒排表的起始位置,利用性質3能夠對搜索的倒排表進行剪枝,從而提高算法效率.

改進后的 TopLCA-K算法的思想是:首先建立每個查詢關鍵字的倒排表,對查詢關鍵字實例的個數從小到大排序,并把每個倒排表中的Dewey編碼按照從小到大的順序排序,逐層建立中心位置索引,根據中心位置索引逐層尋找LCA并進行評分,一直完成最少個數的查詢關鍵字實例的搜索.

建立中心位置索引CI(center index)的方法是:對于XML有向樹T(V,E,r)的關鍵字查詢Q={k1,k2,…,km},查詢關鍵字k1的實例KMS(k1)={a[1,1],a[1,2],…,a[1,t1]},查詢關鍵字k2的實例KMS(k2)={a[2,1],a[2,2],…,a[1,t2]},查詢關鍵字km的實例KMS(km)={a[m,1],a[m,2],…,a[m,tm]}.每個查詢關鍵字實例按照 Dewey編碼從小到大排序,即a[j,1]≤a[j,2]≤…≤a[j,tj](1≤j≤m),且t1≤t2≤…≤tm.構建如下的中心位置索引如圖3所示.第1層存儲了k1實例,第2層存儲了CenterNode(T,KMS(k2),a[1,j])節點,第 3層到第m層存儲了CenterNode(T,KMS(ki),CenterNode(T,KMS(ki-1),a[i-1,j]))節點.

例如,對于圖2所示的XML文檔樹T和查詢Q={BigData,Felix,James},按照前面的方法建立的中心位置索引如圖4所示.

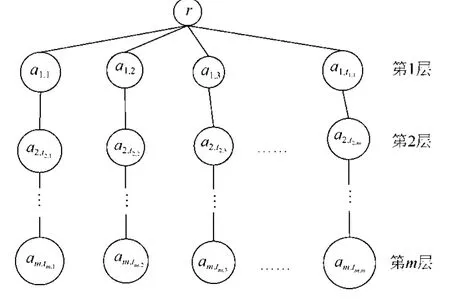
Fig.3 Central location index圖3 中心位置索引

Fig.4 Central location index corresponding to Fig.2 andQ={BigData,Felix,James}圖4 與圖2和查詢Q={BigData,Felix,James}對應的中心位置索引

推論1.XML有向樹T(V,E,r)的關鍵字查詢Q={k1,k2,…,km},對應的中心位置索引CI,第i層的中心位置a[i,ci],LCA(a[1,c1],a[2,c2],…,a[m,cm])=C,a[1,c1],a[2,c2],…,a[m,cm]是 CI樹中一條從葉子節點到第 1層的路徑；LCA(a[1,x1],a[2,x2],…,a[i,ci+k])=R(ci+k≤ti,ti是第i層的關鍵字實例個數),LCA(a[1,x1],a[2,x2],…,a[i,ci-j])=L(ci-j≥0),則如下公式成立:

根據推論1,可以快速尋找出最小LCA的值.圖4顯示了圖2、Q={BigData,Felix,James}的CI.通過樹的第1個分支計算出 LCA為 1.1.3,該節點有 6個葉子,關鍵字與 LCA的聯系度為 11,LCAValue(T,Q,1.1.3)=(6+11)/3=17/3；在第 3層以 1.1.3.1.2.1.1為出發點,從兩邊搜索其他 Felix節點的組合情況,左邊的 Felix節點1.1.2.1.1,則前面兩個節點與1.1.2.1.1的LCA為1.1,現在考慮只有BigData和James兩個節點的情況下LCAValue(T,Q,1.1)=(9+9)/3=18/3,則LCAValue(T,Q,1.1)≥18/3＞LCAValue(T,Q,1.1.3)(=17/3),根據推論 1,可以不用考慮1.1.2.1.1左邊的節點；再觀察右邊的情況,右邊的Felix為1.2.3.2.1,則前面兩個節點與1.2.3.2.1的LCA為1,這種情形下葉子節點有 25個,LCAValue(T,Q,1)=(25+4)/3＞LCAValue(T,Q,1.1.3)(=17/3),根據推論 1,可以不用考慮1.2.3.2.1右邊的節點.因此,利用中心位置索引可以對搜索空間進行快速剪枝,提高了搜索效率.

針對有序XML文檔樹T的關鍵字查詢Q,按照深度優先遍歷T并為每個節點賦予Dewey編碼,然后建立每個查詢關鍵字ki對應的實例節點倒排表,并按照Dewey編碼從小到大地對該倒排表進行排序；建立每個子樹的葉子節點數列表；建立中心位置CI.尋找最佳K個LCA方法,見算法1和算法2.

算法1.getMinLcaValue(T,Q)//取得最小的LCA值.

算法2.getLcaValue(ciT,IL,col,direction)； //根據倒排表IL和CI計算第col個的LCA值.

5 實驗分析

我們設計了一套全面的實驗來評估本文提出的TopLCA-K算法的性能,采用真實數據集SIGMODRECORD、Mondial和DBLP作為測試數據,比較了與XReal、XReason和SLCA等算法在查全率、查準率和時間性能等方面的效果.所有實驗在CPU為Intel雙核3.6GHz,RAM為4GB,操作系統為Windows 7的機器上運行,實現語言為Java SE,通過使用dom4j-1.6.1.jar來解析XML文檔.

5.1 數據集與查詢測試

我們選取了來自于現實情況的SIGMODRECORD、Mondial和DBLP作為測試數據集.表4顯示了這些數據集的統計信息,它們具有不同特征,SIGMODRECORD節點數和不同標簽數最小,Mondial數據集的節點數處于中間水平,使用這兩個測試數據集的主要目的是測試算法的查全率和查準率.DBLP①的規模很大,節點數超過1億,我們選擇的測試數據僅僅是其中的一部分,但也保持了一定的規模,該數據集主要測試在數據規模較大情況下各算法的時間性能.本實驗沒有考慮數據集中ID/IDREF的關聯情況.

Table 4 Data sets表4 測試數據集的基本信息

針對每個測試數據集,我們選取了具有不同查詢意圖的測試查詢,并且每個查詢測試的查詢意圖是明確的.為每個數據集設計了7個測試查詢,S1～S7、M1～M7和D1～D7分別表示針對SIGMODRECORD、Mondial和DBLP數據集的測試查詢.具體見表5.

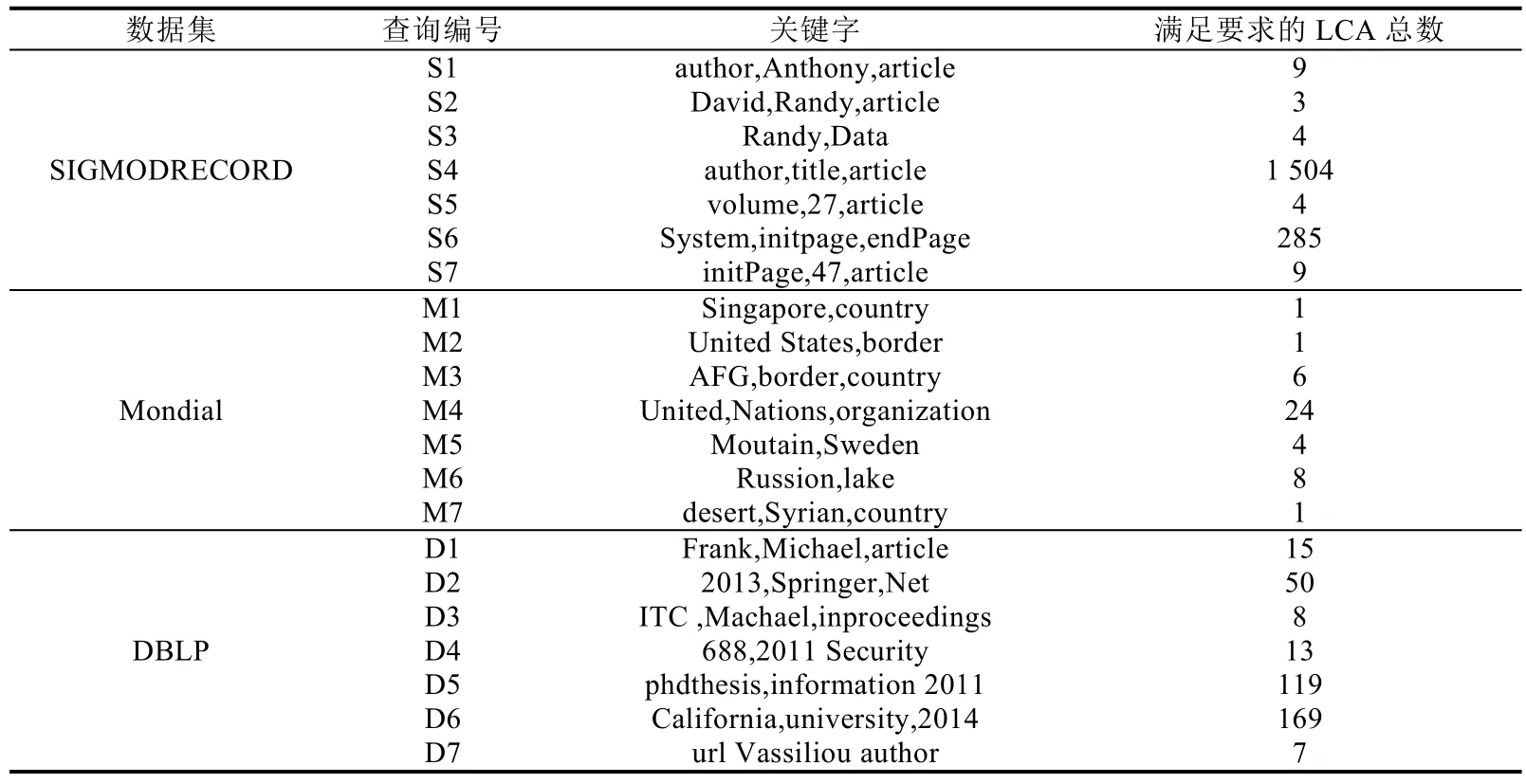
Table 5 Keyword query case表5 關鍵字查詢案例

5.2 查詢質量

把本文提出的TopLCA-K算法與已有XReason、Xreal和SLCA等方法在查準率和查全率進行對比來比較它們的查詢質量.

圖5顯示了本文提出的TopLCA-K與其他方法在查詢準確率方面的比較情況.

圖5顯示,在查準率方面,一般情況下,TopLCA-K要高于其他3種方法,因為該算法考慮了LCA中橫向關鍵字密度和縱向關鍵字密度兩方面的情況,因此排在前面的更符合用戶查詢意圖.但在某些查詢情況下,準確率也不能達到100%,主要是因為查詢關鍵字存在一些歧義,例如關于DBLP數據集的D4查詢,查詢意圖是查詢688頁,2011年出版的標題中含有Security的論文、書籍或者會議出版的文章,但是由于688不僅僅出現在page中,而且在節點ee中也出現了該關鍵字.同理,2011不僅僅出現在year節點中,而且在incollection的url中也出現了2011.

圖6顯示了召回率的比較情況.

很明顯,TopLCA-K的召回率為100%,不存在漏檢問題,其他方法都不能達到100%,XReal采用擴展網頁排名方法進行排名,在關鍵字歧義情況下,很容易漏檢；SLCA由于去掉了父 LCA,顯然會丟失一些符合要求的結果；而TopLCA-K返回了所有的LCA,包括有歧義的LCA,然后從深度和廣度計算LCA的值,把排名小的優先返回,當K值合理時,將返回所有可能滿足查詢意圖的LCA.

Fig.5 Precision rate圖5 比較查準率

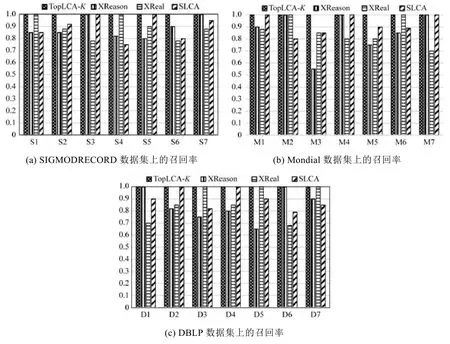
Fig.6 Recall rate圖6 比較召回率

5.3 查詢性能

圖7顯示了3個數據集上算法運行時間情況,為了準確記錄查詢時間,每個關鍵字查詢執行5次,取它們的平均值作為查詢時間,根據規則3設置了TopLCA-K中K的值.從圖7可以發現,TopLCA-K的算法時間性能明顯優于XReason和XReal,與SLCA比較接近.因為TopLCA-K算法利用CI能夠對查詢空間樹進行有效剪枝,例如在D6中,共有8 849個節點包含關鍵字2014,其中year節點值有4 051個,其他節點,如ee包含的2014有520個.這種情況對XReason產生有效結構模式形成了很大干擾,這種情況也對采用TF*IDF排名的XReal方法形成了很多干擾信息.

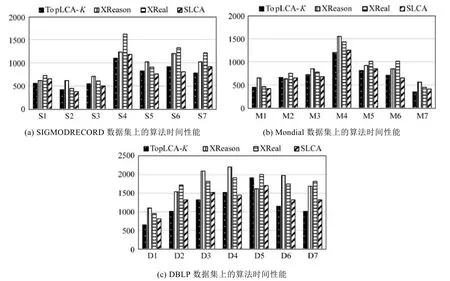
Fig.7 Time performance圖7 算法時間性能對比

6 結束語

本文首先介紹了LCA過濾語義和結果排名方法,指出了在XML關鍵字查詢中LCA過濾語義存在漏報問題,提出了用戶查詢意圖與查詢關鍵字在縱向和橫向方面的兩個規則,建立了利用邊密度和路徑密度對LCA節點進行評分的公式,采取中位節點索引CI來提高TopLCA-K算法效率.實驗結果表明,本文提出的對LCA進行評分排名的方法在查準率和召回率方面效果較好,并且查詢時間性能也較好,但需要進一步優化提高.下一步的研究重點考慮當在LCA之間存在包含、重復和交叉關系情況時,如何對 LCA進行排序以及結果展示的問題,同時進一步優化算法.在未來的工作中,將研究如何減少編碼長度以及基于新編碼方案的 XML關鍵字查詢處理.