異曲同工，萬變歸宗
——基于初中數學折疊問題的教學思考

☉江蘇省昆山市正儀中學 金潔霞

折疊問題是初中數學考查的重點和難點，這類問題能夠較好地考查學生對軸對稱圖形性質與規律的學習水平，這類問題對學生的觀察、動手和綜合應用方面的能力要求高.正因如此，折疊問題一直得到命題專家的青睞，成為各類初中數學考試的熱點問題.本文以一道典型折疊問題及其變式為探究載體，重點剖析其內在本質規律，探究其思維路徑，體現“異曲同工，萬變歸宗”的數學哲學之美，旨在拋磚引玉，以期引起教育同仁的進一步思考與探究.

一、折疊問題的案例及變式呈現

案例：如圖1所示，矩形ABCD中，AB=6，BC=9，E、F分別是AD和BC上任意兩點，線段EF將矩形分成左右兩部分，先將右部分沿著EF折疊，恰好使得C點落至AB邊上的C′點處，且AC′=BC′，D點變為D′，連接C′D′交AE于M點，試求AM的長度.

思維路徑：Rt△MAC′中只有AC′=3可直接得出，而直接在Rt△MAC′中利用勾股定理或三角關系求解AM的長度所需條件不夠，需考慮構建與其他三角形的關系求解. 據折疊原理和幾何圖形關系得：FC′⊥MC′，FC′=FC，則Rt△FBC′Rt△C′AM，即在Rt△FBC′中，運用勾股定理可求出BF=4，則

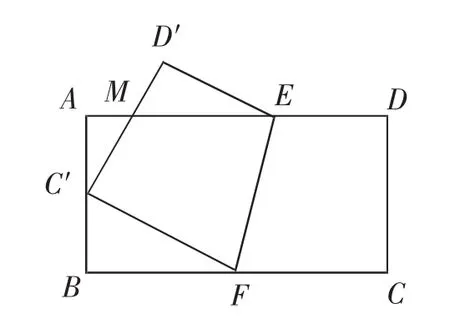
圖1

圖2

變式1——改變折疊背景

題目：如圖2所示，正方形ABCD的邊長為6，E、F分別是AD和BC上任意兩點，線段EF將矩形分成左右兩部分，先將右部分沿著EF折疊，恰好使得D點落至AB邊上的D′點處，且AD′=BD′，C點變為C′，連接C′D′交BF于M點，試求Rt△D′BM的周長.

思維路徑：變式1用正方形代替原矩形作為折疊背景，求周長代替求邊長.但從數學對象的基本關系的本質看沒有新的變化，因此仍然由勾股定理求AE和ED′，再用Rt△D′BM Rt△EAD′求D′M和BM，最終可求Rt△D′BM的周長.

變式2——改變折疊對應點

題目：如圖3所示，矩形ABCD中，AD=12，CD=18，E、F分別是AB和CD上兩點，將矩形沿著EF折疊，C點落于A點，B點落至B′點，試求S△AEF的值.

思維路徑：據題意可知只需求出AE的長度即可得這一面積.據折疊原理可知AF=CF，AB′=BC=12，由幾何關系可知△ADF AB′E，即AE=AF.在Rt△ADF中，運用勾股定理得AF=13，則12=78.

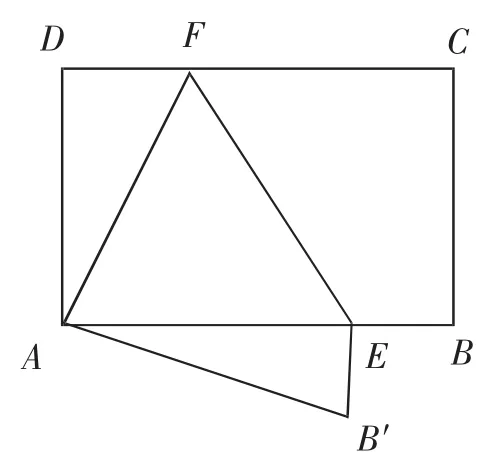
圖3

圖4

變式3——改變折疊對應邊

題目：如圖4所示，矩形ABCD中，AB=2，E、F分別為矩形ABCD中AD和CD的中點，現將△ABE沿著折痕BE進行折疊，點A恰好落至BF上的A′點，試求AD的長度.

思維路徑：根據矩形性質，AD=BC.根據折疊性質，可得A′B=AB=2，△EDF △EA′F，即則BF=A′B+A′F=3.在Rt△BCF中，根據勾股定理，可得

案例及變式的“歸宗”分析：在以上案例及變式中，其形式可以是千變萬化的，但是其命題立意與問題解決的源流可以歸宗為折疊變化的基本關系——全等關系、對稱關系；而折疊背景則提供了具體的數量計算路徑.因此，這類折疊問題為同源同宗的衍生問題.

二、折疊問題的數學教學過程思考

1.立足基本數學關系，奠定折疊問題解決的基礎

（1）重視幾何關系作為解決折疊問題的直接工具作用.首先，要重視幾何關系的梳理與教學：幾何圖形的折疊屬于軸對稱現象，關于折痕對稱的兩個圖形中對應線段長度相等、對應的兩個角度相等，初中數學折疊問題往往建立在“平行四邊形、矩形和正方形”等背景之上，在處理此類折疊問題時應該弄清折疊的背景，解題過程中靈活運用其對應的性質.

折疊問題中求解線段長度、角度大小、幾何圖形的周長等問題，往往涉及三角形相關知識：直角三角形中的勾股定理、直角三角形中兩個銳角互余，等腰、等邊三角形的性質，全等三角形的判定與性質，相似三角形的判定與性質，平行線性質、中位線性質、角平分線性質、垂線定義等.解決實際問題時存在一定的內在規律：對于直角三角形中的長度求解，可以利用勾股定理，對于一般三角形中的邊長，可以利用全等或相似的手段進行求解.

（2）以數學思想的教學提升折疊問題教學的價值.折疊問題在平面、空間、直線上的數量關系，往往涉及較豐富的代數關系，函數思想、方程思想等數學思想，可以借助折疊問題背景進行滲透式教學，從而可設計歸宗于折疊但不拘泥于折疊的教學處理，提升折疊問題教學的數學教育價值.如上述典型案例中的化歸思想體現在：AM長度的求解，借助Rt△FBC′Rt△C′AM進行間接求解；方程思想體現在：案例分析過程中BF長度的求解，將BF作為未知量，運用勾股定理構建方程進行求解.

數學解題離不開數學思想的理論指導，數學思想的靈活運用，有助于學生迅速探尋數學解題的思路，有助于學生獲得有效解題方法的靈感.對于初中數學教師而言，在解題教學實踐中，擺脫“就題論題、機械講解方法”等傳統教學方式的束縛.實踐表明，數學思想是數學解題教學的“內功”支撐點，離開數學思想的數學解題教學，必定是“膚淺、表面”的數學教學，不利于學生數學解題能力的提升，不利于學生數學學科核心素養的提升.

2.構造折疊問題實例，提升學生數學素養

眾所周知，恰當的實例可以為學生問題解決過程的嘗試與素養形成提供練手.因此，教師需要發揮教學智慧構造實例，充分展示處理折疊問題的具體思想與方法.

實例：如圖5所示，矩形ABCD中，AB=3，BC=5，E為CD邊上任意一點，若以BE為折痕，將△BCE進行折疊，C點落至AD上的F點，試求線段CE的長度.

圖5

解析：根據折疊性質可知BF=BC=5，EF=CE，在Rt△ABE中假設CE=EF=x，則DE=3-x.DF=AD-AF=5-4=1.在Rt△EDF中，根據勾股定理，可得即即

點評：本題是以矩形為背景的折疊問題，解題中主要體現折疊性質、勾股定理、轉化思想、方程思想的靈活運用，解題過程清晰、簡練.

三、結束語

數學的形式千變萬化，而對其進行溯源，往往不同形式出于一宗.因此，數學教學有必要深度挖掘教學素材的數學源流，力求教學過程貫通規律探究與思維形成訓練.初中數學折疊問題中，不管問題形式如何變化多端，只需要準確抓住折疊問題的“宗”——折疊的本質（軸對稱的性質），引導學生有機融合相關的數學知識和數學思想方法，使其達到舉一反三的學習效果，對難題能有自己的數學思想與解決方法，進而促進初中學生數學素養的不斷提升.