幾何入門階段習題講評的教學思考與建議
——從一道七上模考幾何填空題講評說起

☉江蘇省清江中學 張紹俊

最近在七年級上冊期末復習階段，一份模考卷上的一道幾何填空題得分率很低，筆者本來準備讓幾個做出答案的學生上臺示范一下他們的解法，沒有想到連續幾個學生雖然獲得解答，但是解法都顯現出不夠優化的情況，這讓筆者即時調整了教學進度，把這節課多數時間花在該題的解題教學進程上.本文給出這道習題的講評手記，并跟進幾何習題講評的相關思考與教學建議，供研討.

一、一道幾何習題的講評手記

考題：以∠AOB的頂點O為端點引射線OP，使∠AOP∶∠BOP=3∶2，若∠AOB=17°，則∠AOP的度數為______.

閱卷記錄：這道填空題全班只有20%的學生填出正確答案（10.2°，51°）.

講評預設：考慮到正確率很低，需要多花一些時間進行講評.為了追求更好的講評效果，決定先安排一位填出正確解答的學生上臺講解他的思路，然后讓學生互相學習、交流.

講評記錄：先讓獲得正確解答的幾個學生站起來，讓其他學生學習，站起來的幾個學生都很有自信，然后安排學生小Y上臺講解他的思路，他寫出兩個算式，如下：

教師追問下面的學生是否看懂了，那幾個正確的學生表示都能理解，但其余的學生仍然表示不太理解.于是教師示意其他學生上臺來構造圖形，更直觀形象地解釋這兩個度數，于是學生小J上臺后在黑板上經過調整得到如下兩個圖形（如圖1、圖2）：

圖1

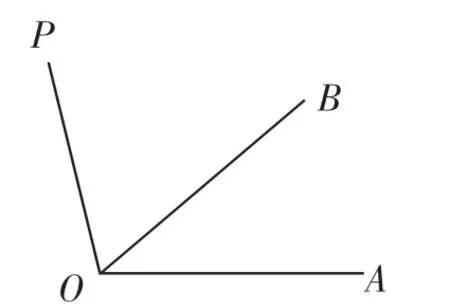
圖2

在兩個圖形的啟發之下，有一半左右的學生表示能理解.接下來是教師跟進講評.

教師講評：學生小Y的兩個算式是典型的“小學解法”，而學生小J的圖形分析更加直觀形象，但是仍然有不足，主要缺陷是圖形不精準，我們應該學會會構造更加精確的圖形，我們應該先畫出相對精準的∠AOB=17°，然后分析射線OP的可能位置，教師接下來示范相對精準的構圖（如圖3、圖4）.

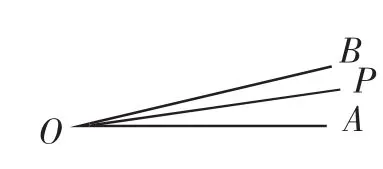
圖3

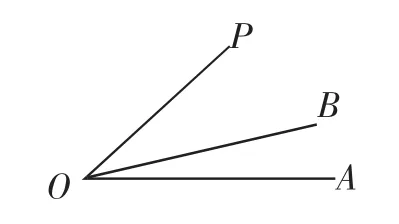
圖4

有了相對精準的圖形分析之后，接下來可以引入方程工具，在圖3中，分別設∠AOP=3x，∠BOP=2x，可得2x+3x=17°，解得x=3.4°，于是∠AOP=3x=10.2°；

在圖4中，分別設∠AOP=3y，∠BOP=2y，可得3y-2y=17°，解得y=17°，于是∠AOP=3y=51°.

綜上，∠AOP=10.2°或51°.

經過上述分析，多數學生都能理解并整理出詳細過程，但是我們的講評仍然在繼續.

解后回顧：同學們雖然覺得這道題較難，但它有一個類似的或者說相同結構的線段習題.

同類習題：已知線段AB=17cm，在直線AB上有一點P，且滿足AP∶BP=3∶2，求AP的長.

學生很快得出如下解法，先畫出圖形，然后分析兩個可能的點P的位置（如圖5），并且分類討論得出AP的長為10.2cm或51cm.

圖5

回到考題：受到線段圖形“兩圖合一”的影響，我們也可將圖3、圖4“合二為一”，得出圖6.

圖6

講評效果：講到這兒，再了解學生對該題的理解與掌握時，大家都表示已經徹底想通了，于是教師再讓學生分小組對這道習題進行改編，自主提出問題并解決，通過學情反饋（變式再練了一道同類題，這里限于篇幅，略去），學生解這類問題的正確率達到82%.

二、幾何入門階段習題教學的思考與建議

1.習題講評要從答案核對走向解法探究

在習題量很大的課堂中，常常是答案核對式的講評為主，這類講評的效果非常低下，往往是會的學生會，不會的學生只是滿足于記錄答案，但并沒有機會深入思考、究錯與理解.只有當一節課中待講評的習題真正降下來、減下來，才可能有時間從答案核對式的講評走向解法探究式的講評.探究解法需要時間，需要學生先有獨立思考，然后經歷小組議論、全班展示、教師評析等全過程，有時對學生并不完整、有漏洞的思路或過程，教師還要引導學生參與優化，直到解題思路完全貫通.

2.幾何入門階段需要訓練精準作圖能力

平面幾何是很多學生進入初中階段學習成績的一個重要分水嶺，有些代數適應性好的優秀學生往往也會對平面幾何問題敬而遠之.以筆者的教學經驗來看，不少平面幾何適應性不好的學生，對于精準圖形的構造常常掌握得不好.比如，上文中學生小J對于17°的大小偏差太大，原因是學生大腦中對于一些特殊角度的適應不好，比如90°、60°、45°、30°，這些特殊角度要通過必要的練習能徒手畫出它們的大致大小，這樣在遇到類似17°這樣的角度時，就可利用45°與30°的差來近似構造出17°角，從而為后續研究提供一個相對精準的平臺.試想，如果像小J構造的圖4一樣，則求出一個角度為51°后會發現與圖4中∠AOP為鈍角是矛盾的，會對解題方向造成偏差，不利于快速解題.特別是，作為入門階段的幾何教學，需要特別重視精準作圖能力的訓練，當學生能對圖形有相對精準的理解之后，對于后續幾何學習十分有利，比如，等腰三角形的形狀、全等三角形的變換研究、不同形狀的直角三角形，等等，都需要精準作圖的基本功.

3.習題講評要重視“讓學”與“究錯”

精心準備習題講評素材之后，需要認真預設講評的組織過程，特別是重視“讓學”與“究錯”環節的設計.這里的“讓學”最主要的方式就是讓學生上臺講解，暴露他們的思路與過程，這樣就可引導其他學生參與分析，學習其中的合理成分，并糾正其中的不足與錯漏.這樣不僅講題的學生能有收益，其他學生也能在這個互動、對話、究錯過程中學習提升.我們見到的很多課堂，常常是教師自己講，一講到底，不給學生上臺講解的機會，當然也看不到學生的錯誤，但這種“掩而盜鈴”式教師一講到底，學生的錯誤也就多出現在限時獨立考試過程中，教師在學生考試之后感嘆：“我講了多少遍，你們怎么還不會？”只有我們平時上課講題時充分放手，讓學生上臺講題、展示，讓一些錯漏、稚嫩、不嚴謹的解法與思路多多顯現出來，教師跟進評析、示范與優化，這樣的教學是精準指導，一定可以促進學生切實提高解題能力.

4.講評后要有“多解歸一”的結構揭示

波利亞在名著《怎樣解題》中對解題之后的回顧反思提出了深刻的指導意見，羅增儒教授對波利亞的解題教學理論做出了“中國解讀”與教學推廣，在很多一線教師中產生廣泛的影響.比如，習題講評之后需要有解后反思的教學階段，具體來說，像上文教學片段中，最后鏈接講評了線段問題，并將兩種可能的圖形“合二為一”，實現了“多解歸一”的結構揭示.事實上，數學解題教學中，很多老師重視的往往是一題多解，對于解法的不斷探究也是一些教學研討QQ群的熱鬧話題，這類研究風氣作為教師的個人興趣無可厚非，但是如果過分偏重于一題多解并積極向學生宣傳自己研究到的一題多解，而缺少必要的優化、簡化，則是不恰當的，因為追求“更初等的解法”或者“回到定義去解題”這種解題觀點應該通過我們的教學向學生傳遞與滲透，往往站得更高，就能看得更全面、更深入，也就能理解多種解法的“殊途何以同歸”，從而引導學生通過做一題、會一類達到通一片.

三、寫在后面

教學即研究.不只是公開課教學、示范課學習、教研組評課等教研活動才需要或值得開展研究，日常教學活動中，我們每天都走進課堂，這是教研活動的“第一現場”，像華東師大李政濤教授所指出的，要十分重視“第一現場”中我們的“現場學習力”的提升.上面提供的教學手記是近期課堂的一次真實場景，筆者的記錄還不是很完整，表達也不夠形象生動，觀點闡釋也以個性化表達居多，期待同行的批評與指正.