“單位圓”引出新知：銳角三角函數(shù)同課異構(gòu)

☉江蘇省無錫江陰實(shí)驗(yàn)中學(xué) 孟協(xié)軍

近讀《中學(xué)數(shù)學(xué)》（下），發(fā)現(xiàn)連續(xù)兩期刊登初中“銳角三角函數(shù)”起始課的教學(xué)設(shè)計(jì)（見參考文獻(xiàn)［1］、［2］），兩位老師的教學(xué)設(shè)計(jì)都體現(xiàn)了“用教材教”（鐘啟泉語），重視了數(shù)學(xué)現(xiàn)實(shí)引入新課，“讓數(shù)學(xué)課講數(shù)學(xué)”（單語）等教學(xué)理念，對(duì)一線教學(xué)有著較好的示范引領(lǐng)作用.受到他們的啟發(fā)，筆者也基于個(gè)人研發(fā)課例的興趣，聯(lián)系高中階段對(duì)三角函數(shù)的學(xué)習(xí)理解，基于“單位圓”研發(fā)一節(jié)初中階段“銳角三角函數(shù)”起始課例，同課異構(gòu)，供研討.

一、銳角三角函數(shù)起始課教學(xué)設(shè)計(jì)

教學(xué)環(huán)節(jié)（一） 數(shù)學(xué)現(xiàn)實(shí)，引出新知

創(chuàng)設(shè)情境：黑板上畫出一個(gè)平面直角坐標(biāo)系，并以原點(diǎn)為圓心，單位1為半徑，作出一個(gè)圓（因?yàn)楸菊n例中會(huì)反復(fù)提及，不妨稱這樣的圓為“單位圓”），設(shè)該圓與x軸的正半軸交于點(diǎn)A.引導(dǎo)學(xué)生把目光聚焦在第一象限，在圓上取一點(diǎn)B（x，y），連接OB，得到∠BOA，設(shè)∠BOA=α，安排學(xué)生分組研究當(dāng)α取定一些特殊的銳角時(shí)，B點(diǎn)的坐標(biāo)能隨之確定.

圖1

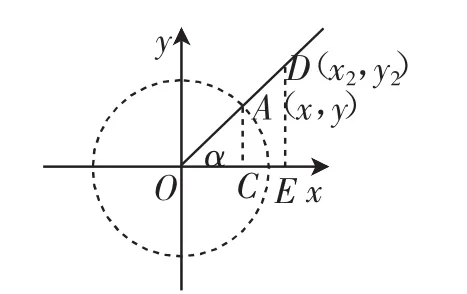
圖2

教學(xué)預(yù)設(shè)：學(xué)生會(huì)取α的一些特殊銳角如30°、45°、60°，進(jìn)而研究出相應(yīng)的點(diǎn)B的坐標(biāo).教師引導(dǎo)學(xué)生走向一般，預(yù)設(shè)如下追問：

追問1：當(dāng)α取定任意銳角時(shí)，點(diǎn)B的坐標(biāo)能否確定？（學(xué)生應(yīng)該可以猜想出能被唯一確定）

追問2：回顧函數(shù)的概念，當(dāng)α取定一個(gè)銳角時(shí)，相應(yīng)的B點(diǎn)的橫、縱坐標(biāo)都會(huì)隨之唯一確定，它們之間具有函數(shù)關(guān)系嗎？（學(xué)生應(yīng)該可以確認(rèn)y與α具有函數(shù)關(guān)系，x與α具有函數(shù)關(guān)系）

追問3：如圖2，在射線OA上任取一點(diǎn)D（x2，y2），繼續(xù)研究x2、y2與銳角α是否具有函數(shù)關(guān)系.（仍然具有函數(shù)關(guān)系，與之前問題是一樣的，只是“一般化”的過程，可以看成是單位圓的放大，如圖3，也可以引導(dǎo)學(xué)生從相似三角形的角度理解它們的一致性）

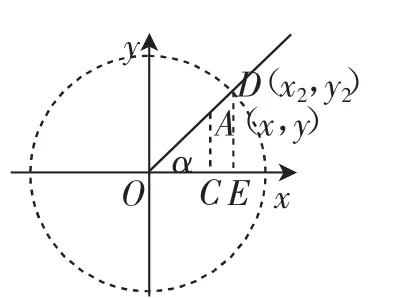
圖3

教師講授：由于這種函數(shù)關(guān)系不同于之前所學(xué)的一次函數(shù)、二次函數(shù)、反比例函數(shù)，這些函數(shù)能用一些代數(shù)式表示，所以歷史上數(shù)學(xué)家們給了它們一些專門的記號(hào)，讓我們把圖形簡化為直角三角形，給出定義（板書如下）：

圖4

說明：板書定義時(shí)，最后補(bǔ)出“銳角”兩字，并強(qiáng)調(diào)初中階段只研究銳角的情況，以后還會(huì)拓展研究范圍更大的角度的三角函數(shù)問題.

教學(xué)環(huán)節(jié)（二） 理解新知，初步運(yùn)用

對(duì)照銳角三角函數(shù)定義，安排學(xué)生計(jì)算30°、45°、60°的三角函數(shù)值，列表梳理出來.由一個(gè)小組派學(xué)生代表到黑板上書寫，如下：

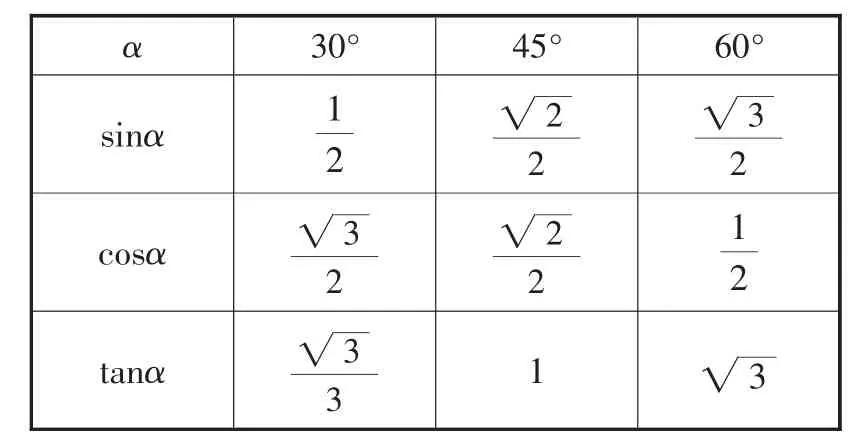
表1

進(jìn)一步研究：既然是函數(shù)關(guān)系，需要研究函數(shù)的自變量與函數(shù)值的關(guān)系，如增減性，同角三角函數(shù)之間的關(guān)系等.學(xué)生先分組交流，然后大組匯報(bào).

預(yù)設(shè)成果：在銳角范圍內(nèi)，正弦函數(shù)sinα的值隨著自變量α的增大而增大；余弦函數(shù)cosα的值隨著自變量α的增大而減小；正切函數(shù)tanα的值隨著自變量α的增大而增大.還有互為余角的兩角的函數(shù)值之間的關(guān)系，如sin30°=cos60°，sin45°=cos45°.如果教學(xué)時(shí)間充分，還引導(dǎo)學(xué)生“走向一般”嘗試證明sinα=cos（90°-α）.

教學(xué)環(huán)節(jié)（三） 引導(dǎo)探究，走向一般

例1計(jì)算：sin230°+cos260°.

變式計(jì)算：sin245°+cos245°.

猜想驗(yàn)證sin2α+cos2α的計(jì)算結(jié)果.

教學(xué)組織：學(xué)生容易計(jì)算出前兩問的值，但是“走向一般”的證明有一定的挑戰(zhàn)，需要“回到定義”，基于直角三角形、結(jié)合勾股定理演算證明.

學(xué)生證明之后，回到開課階段的問題情境，如圖5，基于“單位圓”的基本圖形，可以發(fā)現(xiàn)點(diǎn)B的坐標(biāo)（x，y）也就對(duì)應(yīng)著（cosα，sinα）.在圖5中，結(jié)合勾股定理容易看出sin2α+cos2α=12=1.

學(xué)生理解之后，還可進(jìn)一步“一般化”，將圓的半徑“單位1”變式為參數(shù)r，引導(dǎo)學(xué)生驗(yàn)證確認(rèn)：sin2α+cos2α=r2.

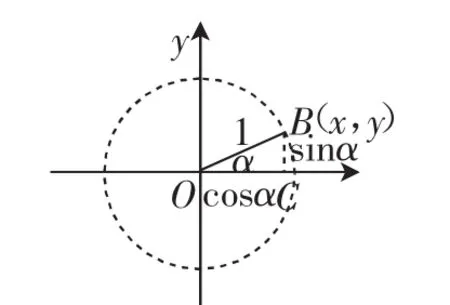
圖5

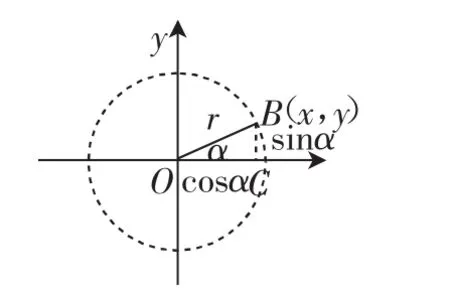
圖6

教學(xué)環(huán)節(jié)（四） 課堂小結(jié)，反饋檢測

小結(jié)問題1：結(jié)合“單位圓”基本圖形說說你對(duì)本課所學(xué)的三種銳角三角函數(shù)的理解；

小結(jié)問題2：本課學(xué)習(xí)了哪幾個(gè)特殊銳角的三角函數(shù)值？你是怎樣理解或快速記憶那個(gè)特殊銳角三角函數(shù)值表格中的數(shù)值的？

小結(jié)問題3：銳角三角函數(shù)需要在直角三角形中進(jìn)行分析與思考，與直角三角形的各邊大小有關(guān)系嗎？舉例說說.

反饋檢測題：

題1：在平面直角坐標(biāo)系xOy中，點(diǎn)A的坐標(biāo)是（1，2），畫圖分析∠AOx的正弦函數(shù)值、余弦函數(shù)值、正切函數(shù)值.

題2：在直角三角形ABC中，∠C=90°，∠B=60°，利用銳角三角形函數(shù)的新知，求證：AB=2BC.

題3：在三角形ABC中，AB=10，BC=6，AC=8.分別求sinA、cosA、tanA的值.

題4：結(jié)合銳角三角函數(shù)定義證明：sin41°=cos49°.

二、教學(xué)立意的進(jìn)一步闡釋

1.核心概念的起始課值得深入研討

我們知道數(shù)學(xué)中有很多核心概念，代數(shù)中如數(shù)的運(yùn)算法則、運(yùn)算通性，方程，函數(shù)等，都是核心概念，可以發(fā)現(xiàn)，核心概念常常是指那些具有寬廣發(fā)展前景的數(shù)學(xué)概念.本課例中關(guān)注的三角函數(shù)的概念就屬于這類核心概念，它有著十分寬廣的發(fā)展前景，只是在初中階段剛剛涉及很少的部分.就目前所見的版本的初中教材，多是從生活現(xiàn)實(shí)出發(fā)，為了解決某些直角三角形的生活應(yīng)用問題，而引入正切函數(shù)，進(jìn)一步引出正弦函數(shù)、余弦函數(shù)，這種基于生活現(xiàn)實(shí)引入新知的方式也是可以的，體現(xiàn)了數(shù)學(xué)來源于生活.但是對(duì)于三角函數(shù)這樣的核心概念，不只是在生活中有廣泛應(yīng)用，它更是一個(gè)邏輯連貫、前后一致的知識(shí)模塊，也可以從后續(xù)（主要是高中階段）三角函數(shù)概念教學(xué)需要出發(fā)，基于數(shù)學(xué)現(xiàn)實(shí)（如本文關(guān)注的“單位圓”）引出新的概念，這樣學(xué)生到高中續(xù)學(xué)三角函數(shù)時(shí)，就可進(jìn)一步放開角度的研究范圍，拓展開去，走向一般.在這個(gè)意義上說，作為核心概念的三角函數(shù)起始課值得反復(fù)研討、深入研討，而不是簡單停留在“教教材”層面上.

2.加強(qiáng)不同教學(xué)環(huán)節(jié)的“前呼后應(yīng)”

在上文課例中，我們選定了“單位圓”作為數(shù)學(xué)現(xiàn)實(shí)引出新知后，在不同教學(xué)環(huán)節(jié)都圍繞著“單位圓”開展教學(xué)，將其作為一個(gè)重要的問題背景（或平臺(tái)），做到了互相關(guān)聯(lián)、前后呼應(yīng)，當(dāng)然這也是踐行所謂“問題驅(qū)動(dòng)”式的教學(xué)設(shè)計(jì)與課例研究.這里不妨對(duì)“問題驅(qū)動(dòng)”式教學(xué)設(shè)計(jì)做出進(jìn)一步解讀，我們所指的問題是指少而精，富于生長，前景廣闊的問題情境，而不是那種“一題接一題”的習(xí)題式推進(jìn)，讓一個(gè)主干問題能引發(fā)、生長、變式、拓展到很多問題串，而且問題串之間互相聯(lián)系、層層遞進(jìn)，這樣就是品質(zhì)較高的問題驅(qū)動(dòng)，而不是“習(xí)題單式”的題海戰(zhàn)術(shù).

3.重視教學(xué)追問與學(xué)情反饋的設(shè)計(jì)

在課例的框架或主干問題確定之后，需要預(yù)設(shè)各個(gè)主干問題之下的教學(xué)追問，而不是簡單的即興追問（踩著西瓜皮，滑到哪里是哪里），精心預(yù)設(shè)的系列追問形成問題串，對(duì)所學(xué)新知起到有效鞏固、反復(fù)強(qiáng)化的教學(xué)功能.當(dāng)前我們看到一些導(dǎo)學(xué)案之所以習(xí)題量偏大，淪落為習(xí)題單式的習(xí)題教學(xué)，原因就是對(duì)有些主干問題的認(rèn)識(shí)不夠，沒有充分抓住核心習(xí)題、經(jīng)典習(xí)題進(jìn)行系列變式，預(yù)設(shè)問題串，又要顧及增加所謂課堂訓(xùn)練容量，從而就大量選題，對(duì)不同習(xí)題之間的關(guān)聯(lián)度、一致性缺少深度構(gòu)思，這是讓人遺憾的.就本課例最后提供的幾道原創(chuàng)學(xué)情反饋題，也可順便解讀一下設(shè)計(jì)意圖，作為新授課的必要學(xué)情反饋，需要關(guān)注學(xué)生對(duì)新概念的理解是否深刻，是否掌握了“回到概念去解題”的思維方法，都可以通過這幾道小題得到反饋.

三、寫在后面

經(jīng)典課例的同課異構(gòu)、反復(fù)研討能加深我們對(duì)核心概念的理解角度與深度.正是基于 以上認(rèn)知，我們基于“單位圓”的數(shù)學(xué)現(xiàn)實(shí)，提供了銳角三角函數(shù)的起始課教學(xué)設(shè)計(jì).因?yàn)樵撜n例開放度大，對(duì)教師課堂駕馭要求高，也許對(duì)初任教師并不具有推廣性，期待有豐富的駕馭課堂經(jīng)驗(yàn)的教師上課實(shí)踐，并跟進(jìn)打磨，不斷豐富該課例的教研資源.