四川盆地東部下志留統龍馬溪組頁巖氣藏應力敏感性及其對產能影響的定量評價

張國強

(中石化江漢石油工程有限公司井下測試公司，湖北 武漢 430000)

近年來，頁巖氣藏開采發展十分迅速。作為決定頁巖氣產能的重要因素，頁巖滲透率決定了頁巖氣在低滲儲層中的流動方式。頁巖滲透率具有明顯的應力敏感性，在地應力場作用下，頁巖滲透率展現出復雜的變化特征。水平井+水力壓裂是頁巖氣儲層的重要開采模式，該模式下，水力裂縫提供的高滲透率通道主導前期產能，基質滲透率主導后期產能。因此，明確頁巖滲透率的應力敏感特性征對于定量評價頁巖氣產能具有重要意義。

張睿等[1]通過開展龍馬溪組頁巖巖心孔滲應力敏感測定試驗，提出孔滲冪指數越大，滲透率應力敏感性越強。Dong等[2]通過物理試驗建立了針對車籠埔斷層頁巖樣本的孔隙度-滲透率模型，測試中通過改變圍壓獲得樣本滲透率應力敏感關系曲線，其研究認為增加應力導致的頁巖滲透率損傷是部分不可逆的。姜宇玲等[3]采用脈沖衰減儀器測試龍馬溪組頁巖應力敏感性對滲透率的影響，避免了有效應力對初始滲透率的傷害造成的干擾，分析了圍壓和內壓對滲透率測試的影響。此外，還可以通過建立模型的方法從理論上表征頁巖滲透率的應力敏感性，該類模型通常考慮滲透率與圍壓變化的回歸規律、孔隙壓縮系數、等溫吸附效應、氣體擴散、孔隙彈性力學理論等[4～8]。Zhang等[9,10]從微觀孔隙結構和彈性力學性質的角度出發，建立了針對頁巖的應力-滲透率解析模型，指出頁巖對有效應力的敏感性高于砂巖。

上述研究主要著眼于通過試驗和理論方法確定圍壓變化與滲透率變化的關系，而較少對頁巖滲透率應力敏感性與頁巖氣藏產能的關系展開研究。因此，筆者通過四川盆地東部下志留統龍馬溪組頁巖氣藏應力敏感性試驗獲得滲透率變化規律，使用有限元方法建立流固耦合數值模型，定量評價應力敏感性對頁巖氣藏水平井開采模式產能的影響。

1 頁巖樣本應力敏感性試驗

試驗在常溫常壓下進行，使用氮氣作為天然氣的模擬氣體。所用樣本為取自四川盆地東部下志留統龍馬溪組的頁巖巖心。試驗前，先將巖心在烘箱以70°C恒溫加熱50h制作成樣本，測量其長度、直徑及原始滲透率等基本參數，如表1所示。然后，使用“壓差-流量法”進行氣體單相滲流試驗。試驗的圍壓設備使用高精度多級柱塞驅替壓力泵。試驗中，將圍壓先加至4MPa，回壓加至2MPa，保持注入壓力為3MPa不變。再調整圍壓大小以改變有效應力，記錄下圍壓增加過程中不同狀態下對應的滲透率。當圍壓升至22MPa時，開始逐步降低圍壓并測定卸壓過程中的滲透率變化情況。在圍壓的加壓-卸壓過程中，選取的圍壓節點分別為4、5、7、9、11、13、16、19、22MPa。

表1 頁巖巖心樣本基本參數

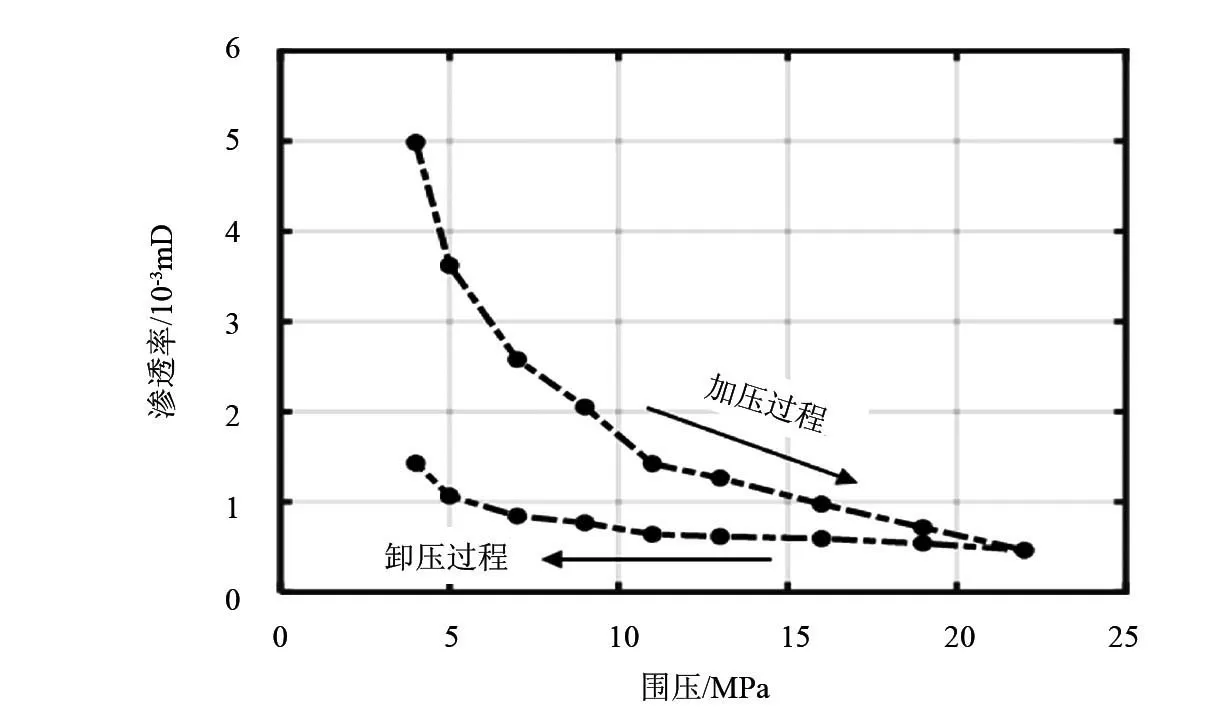
圖1 頁巖樣本圍壓與滲透率變化關系曲線

根據上述試驗步驟進行不同圍壓下的氣測滲透率試驗，所得結果如圖1所示。從圖1可以看出，加壓過程中，滲透率有明顯的下降，從最初4MPa圍壓時對應的0.005mD降至最高22MPa圍壓時的0.0005mD，滲透率降至了初始狀態的10%，表現出了較強的應力敏感性特征。隨后的卸壓過程中，頁巖樣本滲透率由最低的0.0005mD恢復至4MPa圍壓時對應的0.0014mD，說明圍壓循環過程中的滲透率損傷是一個不可逆的過程：加壓造成的滲透率下降不會因為卸壓而完全恢復至初始狀態。該試驗中，卸壓后滲透率(0.0014mD)僅恢復至初始狀態(0.005mD)的28%，不可逆性較明顯。該不可逆性是圍壓增加導致的孔隙喉道封堵造成的，孔隙喉道出現的封堵不會因為圍壓卸去而完全消除，因而造成永久性頁巖滲透率損傷[4]。

2 應力敏感性流固耦合模型

2.1 流固耦合模型

流固耦合模型可以同時計算頁巖儲層中滲流場和地應力場的演化過程，而應力變化和滲透率演化分別是地應力場和滲流場的重要影響因素，因此，頁巖流固耦合模型建模可以明確應力敏感性與頁巖氣藏產能之間的聯系[11～13]。

采取全耦合方法建立流固耦合問題控制方程，并通過彈性模量擬合表示非線性彈性變形。

由達西定律得到滲流速度：

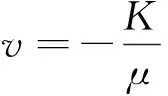
(1)

式中：v為氣體滲流速度，m/s；K為頁巖滲透率，mD；μ為流體黏度，Pa·s；▽p為壓力梯度，Pa/m。

由質量守恒方程和流體擴散方程得到流動方程：

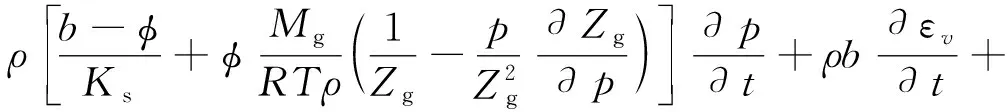
(2)

式中：ρ為流體密度，kg/m3；φ為孔隙度,%；b為比奧系數,1；Ks為固體體積模量，GPa；Mg為氣體摩爾質量,g/mol；R為氣體常數,J/(mol·K)；T為溫度，K；Zg為壓縮因子,1；p為孔隙壓力，Pa;εv為體積應變，1；t為時間，s；▽(ρv)為流體流動的散度。

由固體力學應力平衡得到位移方程：

▽[σ-b(p-p0)I]=0

(3)

式中：▽為表示梯度的Nabla算子；σ為總應力二階張量；p0為初始孔隙壓力，Pa；I為單位矩陣。

式(3)表示全耦合形式下的滲流場與地應力場耦合，比奧系數b是Biot[14]提出的孔隙彈性力學理論中的重要概念，表示飽和流體孔隙介質發生固結作用時的壓力和位移的關系。

試驗時，氣體流動會造成克林肯勃格效應，因此需要進行修正如下：

(4)

式中：Kg為試驗測得滲透率,mD；bk為針對龍馬溪頁巖的修正參數[7],Pa；pavg為平均壓力，Pa。

同時，滲透率也是孔隙度的函數，表示如下：

(5)

式中：γ為修正系數,1；K0為初始頁巖滲透率,mD；φ0為初始頁巖孔隙度,%。此處，初始代表樣本開始測量時的狀態。

之后，使用有限元方法和有限差分方法對公式進行離散，使用Newton法將非線性問題進行線性化，獲得數值解。

2.2 應力敏感性修正

由試驗數據可建立圍壓與滲透率的關系曲線，在耦合模型中，可以通過非線性彈性變形表征該關系。非線性彈性變形可表征非線性應力-應變關系， Scott[15]認為可以通過改變固體彈性模量的方法來表征該關系。因此，在加入應力敏感性修正項時，筆者使用了彈性模量E與圍壓σc的函數關系進行表征：

E=f(σc)

(6)

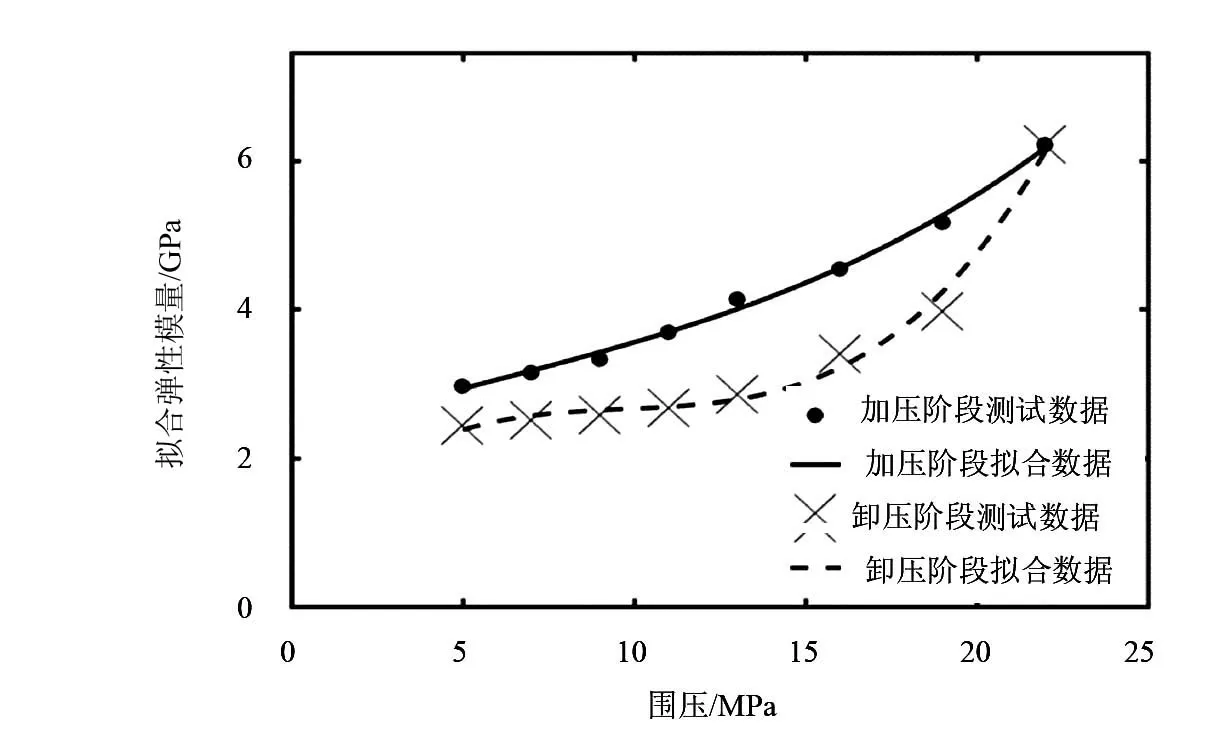
圖2 彈性模量擬合結果

為了得到式(6)的具體形式，結合上述耦合模型，進行試驗數據的擬合。擬合步驟如下：①初始設定一個彈性模量值，在一定的圍壓下代入耦合模型；②根據模型數值解得到平均滲透率；③如果該平均滲透率等于該圍壓下試驗測得的滲透率，說明彈性模量設定值準確，否則，更改設定彈性模量值再次進行計算，直至模擬所得平均滲透率等于試驗測得的值。需要注意的是，對于同一個圍壓值，圍壓狀態可能是加壓或者卸壓，對應的滲透率不同，因此所擬合出的彈性模量也會不同。該過程所得彈性模量擬合結果如圖2所示。

由圖2可知，圍壓加壓過程中，擬合得到的彈性模量持續增大。這是因為加壓過程壓實巖體導致彈性模量增大，應力-應變關系顯示出非線性規律，在最大圍壓為22MPa時，對應最大彈性模量；在卸壓過程中，由于壓實作用減小，彈性模量也呈減小趨勢；由于加圍壓導致的滲透率損傷是部分不可逆過程，加壓和卸壓階段相同圍壓下根據滲透率擬合出的彈性模量不相同。卸壓階段擬合的彈性模量比加壓階段相同圍壓對應的擬合彈性模量小。圖2中所示的擬合曲線可以用式(6)表達，將式(6)嵌入流固耦合模型中，即可得到該頁巖樣本考慮了非線性彈性變形的流固耦合模型。

3 產能影響定量評價

建立考慮非線性應力-應變關系的流固耦合數值模型后，通過算例計算定量分析應力敏感性影響下滲透率、應力和產能的關系。

3.1 巖心尺度模擬

圖3 巖心尺度下的三維圓柱體模擬模型

首先，建立巖心尺度的數值模型網格，針對圍壓循環過程進行數值模擬，表征巖心內相關變量的變化情況。根據表1巖心尺寸參數，建立如圖3所示的三維圓柱體模型模擬流動和變形情況。初始時刻模型內孔隙壓力等于入口壓力，開始流動后模型內出現壓力降。當氣體流動達到穩定狀態后，記錄得到的數值模擬結果。

圖4為加壓狀態下不同圍壓下沿巖心軸向方向的滲透率、滲透率空間導數、孔隙度、最小主應力數值模擬結果，加壓狀態下圍壓分別為5、9、13、19MPa。軸向位置為0時代表巖心入口處，為3.94cm時代表出口處。

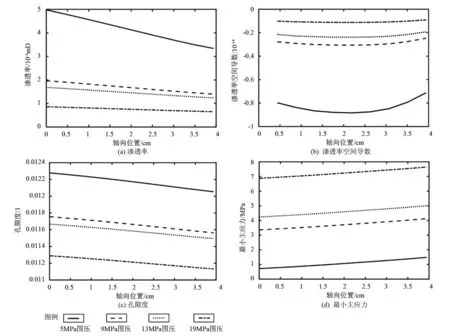
圖4 加壓狀態下不同圍壓下滲透率、滲透率空間導數、孔隙度和最小主應力沿巖心軸向分布模擬結果

圖5 頁巖氣藏水平井產能評價模型

由圖4可知，滲透率沿軸向減小，與孔隙壓力分布梯度相關。同時，圍壓增大造成滲透率快速下降。孔隙壓力梯度也使孔隙度沿軸向減小，圍壓增大也造成孔隙度減小。式(5)可以解釋圖4中滲透率和孔隙度的相似空間分布趨勢。最小主應力沿軸向增大，且隨圍壓增加而增加。圍壓增加說明壓實作用變強，對應著主應力增加；與初始狀態相比，孔隙壓力的變化越靠近出口處越大，導致有效應力沿軸向升高，造成最小主應力沿軸向增大。

3.2 應力敏感性對產能的影響

為了評價應力敏感性對頁巖氣藏水平井產能的影響，筆者建立了水平井尺度數值模型，以模擬不同應力條件下頁巖氣藏水平井產能的變化情況。圖5是頁巖氣藏水平井產能評價模型，該模型中包括1口水平井和6條離散水力裂縫。模型具體參數見表2。模擬時采用彈性模量和應力的函數關系表示應力敏感性。

表2 產能評價模型參數

圖6 不同應力狀態對總產氣量的影響

使用該模型模擬4種不同應力狀態下的產能情況，結果如圖6所示。不考慮應力敏感性的情況下,滲透率未受到損傷，因此總產能最高。考慮應力敏感性時，由于出現彈性模量變化和滲透率變化，對應產能也出現變化。不考慮應力敏感性時300d內總產氣量為7.33×104m3；應力為13MPa時總產氣量為6.81×104m3，相比不考慮應力敏感性下降7.09%；應力為15MPa時總產氣量為6.73×104m3，相比不考慮應力敏感性下降8.17%；應力為17MPa時總產氣量為6.65×104m3，相比不考慮應力敏感性下降9.24%。

4 結論

1)頁巖氣測滲透率應力敏感性試驗說明應力對滲透率的損傷不可能隨著卸壓完全消除。使用彈性模量變化可表達這種現象。

2)試驗中，同一個圍壓值對應圍壓加壓階段和卸壓階段2種情況，其對應的彈性模量擬合結果也不同。加壓階段彈性模量較大，卸壓階段彈性模量較小。

3)沿巖心軸向的數值模擬結果分布受到巖心入口到出口的孔隙壓力梯度影響。靠近出口處的滲透率和孔隙度較低，最小主應力較大。

4)應力敏感效應對頁巖氣產能有較強影響。算例顯示，如果不考慮非線性應力敏感性，總產能計算結果可能被高估。