增長型時間序列組合模型設計及醫院費用預測實證比較*

李望晨 井 淇 姚 琳 張利平△

1.濰坊醫學院“健康山東”重大社會風險預測與治理協同創新中心(261053) 2.濰坊醫學院經濟管理學院

時間序列分析常見于經濟、管理、衛生、醫療領域指標預測問題,它以預測事物本身隨時間變化數據規律來提取信息,以數學方法擬合歷史數據并外推預測未來。擬合預測精度最受應用工作者關注[1]。時序資料表現為隨時間變化呈平滑遞增趨勢特點,無明顯擾動、周期性或季節性,曲線擬合法、ARIMA法為常見方法,算法原理不同但擬合外推性能較好[2]。組合預測模型設計目的是集結每種方法優點,提高擬合性能及外推預測效果。本文針對此類資料特點探索幾種組合建模方法,通過案例比較和驗證組合建模方法對醫療費用預測的意義。

單項方法

經濟或衛生領域某些指標變化規律往往符合平穩增長特點,如住院人次、衛生費用[3]、門診人次[4]、衛生投入、醫院效益等,此類資料組合預測模型設計有相似通用意義。

設某醫院費用某指標時序資料,t1～t13為歷史數據,t14為待預測數據,見表1。

表1 某醫院費用某指標時序資料(萬元)

針對時序資料先以單個方法建立模型,再考慮從多個視角建立組合模型,分析組合設計特點并比較擬合外推性能,為類似增長趨勢變化特點的預測問題提供參考。

1.曲線擬合法

應用前提是歷史數據隨時間呈較平滑曲線變化特點,在自身數據與時間t之間建立函數關系yt=f(t),并用曲線(如直線、拋物線、指數曲線、邏輯曲線等類型)描述關系,有時會有多種類型均適用,可在繼續計算增長特征以后選擇最優者,即用差分法尋求增長特征,精確描述序列數據變化特點并與曲線模型理論增長性質比較。

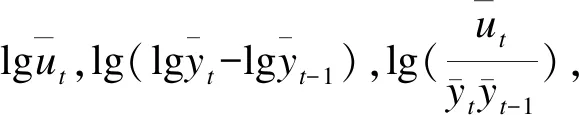
2.ARIMA法

ARIMA法用于平穩序列分析,對遞增趨勢數據須作低階差分,差分過度也會喪失信息。序列數據須先作純隨機檢驗,檢驗是否有建模分析意義。首先確定模型結構和階數,可以低階試取或自動尋優,接下來用條件最小二乘法識別參數以檢驗參數顯著性。建模以后須檢驗信息是否提取充分,對殘差序列作純隨機檢驗。ARIMA法建立歷史序列和殘差序列線性關系,卻不易直觀解讀數據隨時間的真實變動規律。

3.獨立驗證

該時序資料有增長趨勢,作為非平穩序列須作二階差分,通過純隨機檢驗,由低階到高階逐步試取模型結構。(1+0.20501B+0.4373B2)(1-B)2xt=εt為最終識別模型。殘差序列作純隨機檢驗,延遲6階P=0.4838>0.05,自相關系數為0.101,0.108,0.322,0.174,0.176,0.030;模型對原始數據信息提取已經較充分,外推預測值25002.71,95%置信區間[23345.98,26659.43]。對歷史數據擬合4731.68,5367.35,6230.68,7273,9236.36,10854.88,13728.62,14626.73,19121.26,23312.13。兩類方法對歷史數據擬合并計算殘差序列。

由此分別計算平均相對誤差絕對值2.52%、5.37%。分別演示擬合效果,見圖1～2。

圖1 修正指數曲線擬合外推效果

圖2 ARIMA法擬合外推效果

曲線擬合法適于趨勢增長數據平滑修勻,歷史數據擬合好,近期增長趨勢有類似“拐點”特點,若以指數遞增外推未來而引起“樂觀”預測;經差分后以ARIMA法提取序列短期相關性,ARIMA法反映歷史數據長期變化,擬合效果也很好,但對后期快速增長趨勢難以適應,會引起“悲觀”預測。于是引入多種組合設計思路折中分析并檢驗擬合外推效果。

組合方法

上述方法數學理論不同、信息應用有差異,組合設計擬合性能或外推精度一般會更優,線性加權思路常見[5],即以多種思路將歷史擬合值與原始值接近為依據計算權重,將代表方法加權合成組合模型,進一步提高擬合及預測精度。

1.SSE倒數法

兩類方法建模擬合后得殘差序列e11,e12,…,e1t與e21,e22,…,e2t。然后計算Q1=143794.15,Q2=571579.14。取倒數并歸一化為權重w1=0.799,w2=0.201。兩類方法預測值加權組合:0.799×28005+0.201×25002=27401。

2.關聯分析法

兩類方法擬合為歷史數據,計算與真值序列灰色關聯系數:0.794,0.672,0.573,0.851,1,0.520,0.637,0.942,0.346,0.420;1,0.917,0.896,0.648,0.876,0.579,0.756,0.410,0.525,0.669。分別合成灰色關聯度γ1=0.6756,γ2=0.75275。計算權重w1=0.4815,w2=0.5185。兩類方法預測值進行加權組合0.4815×28005+0.5185×25002=26447。

3.相關分析法

兩類方法擬合歷史數據,分別計算與原始序列相關系數:r1=0.998,r2=0.994。計算權重w1=0.5010,w2=0.4990。兩類方法預測值加權組合:0.5010×28005+0.4990×25002= 26502。

4.待定值法

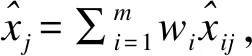
5.平均法

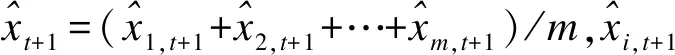
6.結果列舉

不同方法平均相對誤差ME和外推預測值F,見表2。

表2 不同方法實施方法的結果比較

討論

衛生領域許多指標數據隨時間變化呈穩定遞增特點,無周期性、季節性、強干擾性和波折性,曲線擬合法和ARIMA法為兩類時間序列分析方法。曲線擬合法中有許多類型,由數據資料平穩遞增特點分析,根據曲線理論性質與數據變化特點匹配,以增長特征法選擇模型。

通過文中增長型醫院費用案例探索性設計多類組合模型并對數據集選擇、模型特點和結果分析進行解讀。由表1分析,實例資料數據有明顯指數曲線變化特點,曲線擬合法擬合較好,外推時會對增長趨勢慣性延續反映;ARIMA反映早期平緩變化以及長期變化特點,低估中后期增長趨勢[6]。根據兩類建模思想進行組合分析,確保擬合性能條件下改善外推精度。將多種組合方式給予流程簡述和案例演示,兼顧不同方法原理以及擬合性能,緩解對歷史資料過擬合,“中庸折合”后提高外推預測精度。如果此規律慣性延續,則兼顧多類組合模型優點,而將其預測值均數26491折中為參考值,多類組合方法有綜合設計意義。

SSE倒數法、關聯分析法、相關分析法、待定值法、平均法從理論可解釋性、操作可行性角度給出單項方法組合方法,設計過程中單項預測方法作用以較大權重來體現,如SSE倒數法是從殘差平方和最小角度、關聯分析法是從擬合序列與真值序列灰色關聯系數最大角度、相關分析法是從擬合序列與真值序列相關系數最大角度、待定值法是從最小化組合模型殘差優化分配系數角度、平均值法是從假設各單項方法等量體現權重角度。擬合效果或相對平均誤差均不錯,而SSE倒數法對于歷史數據擬合效果更佳;所有模型共同使用的外推預測結果折中分析更有均衡或綜合的實際參考價值。

經分析,曲線擬合法擬合性能好,外推時過度反映增長趨勢而高估預測值;ARIMA法擬合非最好,外推時反應早期平緩規律而低估預測值。近期不可控變動因素引起趨勢增長不平穩,趨勢變化“偏離”歷史慣性,ARIMA法以歷史資料為依據修正。組合建模方式均衡歷史規律擬合效果,緩解過度擬合或擬合不足問題,在保證擬合效果的前提下,折中互補并改善外推預測效果。倘若時間序列不僅有遞增發展趨勢,還有周期性或季節性變化特點,當然亦可由季節指數或季節差分法來提取周期性信息,才能對于消除周期性信息以后的增長型序列參照上述組合方法擬合建模,充分挖掘序列復雜信息并提高預測精度。

時間序列方法多用于歷史擬合以后短期外推應用,歷史數據體現了過去或近期事物發展規律,樣本量選取多少也不能一概而論,不同時期歷史數據反映不同時期延續變化規律信息,歷史信息過度擬合反而降低近期外推性能,將其過度納入反而污染了近期信息而導致預測效果變差。數據資料選擇要根據方法原理理論、實際數據特點、信息復雜程度和專業行業經驗來綜合優選設計,從而科學輔助管理決策工作。