基于清晰度強調的彩色印刷圖像處理研究

袁春雨，舒忠

（荊楚理工學院，荊門 448000）

0 引言

在圖像處理技術應用中，由于圖像獲取、處理、輸出過程不可避免地存在一些制約因素，如：圖像獲取的成像方式、成像部件的性能、量化編碼過程、圖像成像外界光源等方面存在的缺陷、數字圖像處理的方法運用、圖像輸出方式、輸出設備性能等諸多因素，都可能造成圖像信息的丟失或變化（主要指不利變化），從而影響圖像的清晰度。

圖像銳化技術方法實現主要包括有參數控制法和無參數控制法兩種[1]。

在基于像素特征的有參數控制法應用中，主要應用的理論包括：核回歸函數算法、去抖算法（主要應用于相機的拍攝）、點擴散函數（圖像邊緣銳化）和目前常用的全變分、基于圖像稀疏性描述的圖像先驗算法[2-5]。目前的有參數控制法采用高頻濾波與去噪結合，采用局部控制方式處理圖像，因此，還是會出現“漏網之魚”，去噪效果不完整，且運算量也比較大。

無參數控制法是針對像素特征完成模糊像素進行修復的銳化算法，分為一階微分銳化算法（Roberts算子、Prewitt算子、Sobel算子等）、二階微分銳化算法（Laplacian算子、log算子、雙閾值Canny算子等）兩類，后續還出現了一二階混合銳化算法（一階采用乘法運算和二階采用加法運算相結合的銳化算法）和統計銳化算法（沃利斯統計差分銳化算法）等[6-8]。其中，以二階微分銳化算法為基礎的改進算法特別多，如：Photoshop的USM銳化算法、自適應雙邊濾波銳化算法、幾何局部自適應銳化算法，等等。

1 印前圖像銳化算法設計

本文的圖像銳化算法主要設計工作包括：①CMYK模式圖像的數學描述分析；②設計原理分析及設計流程的制定。

1. 1 CMYK圖像的數學描述

CMYK模式圖像的信息使用油墨印刷的網點面積率值進行描述，通過四個通道的取值0～100（由亮變暗，單位為%）反映圖像的階調層次變化。

CMYK圖像某一個像素點數學表達式為：

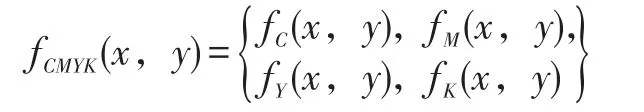
其中，

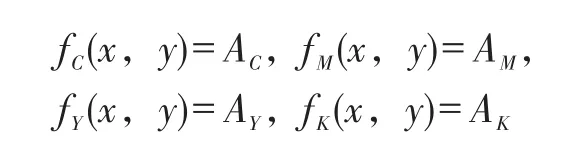
AC、AM、AY、AK分別表示CMYK四色的網點面積率，0≤AC、AM、AY、AK≤100（取整數），x、y用于描述像素矩陣中的橫向和縱向坐標值。

由于印刷圖像通常只針對靜止圖像，則一幅靜止的、像素為M×N（橫向和縱向）的CMYK圖像的數學解析式為：

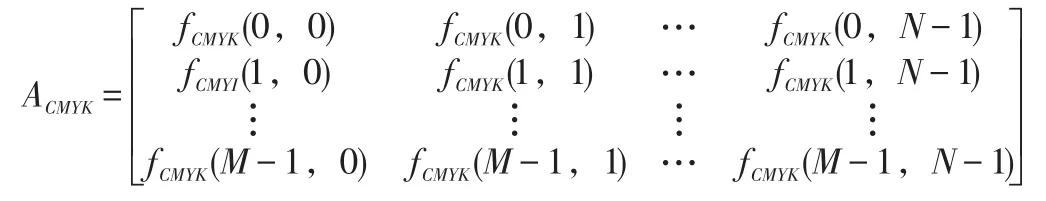
1. 2 設計原理

依據奧布萊恩效應、馬赫帶效應原理，所設計的圖像銳化原理如圖1所示。

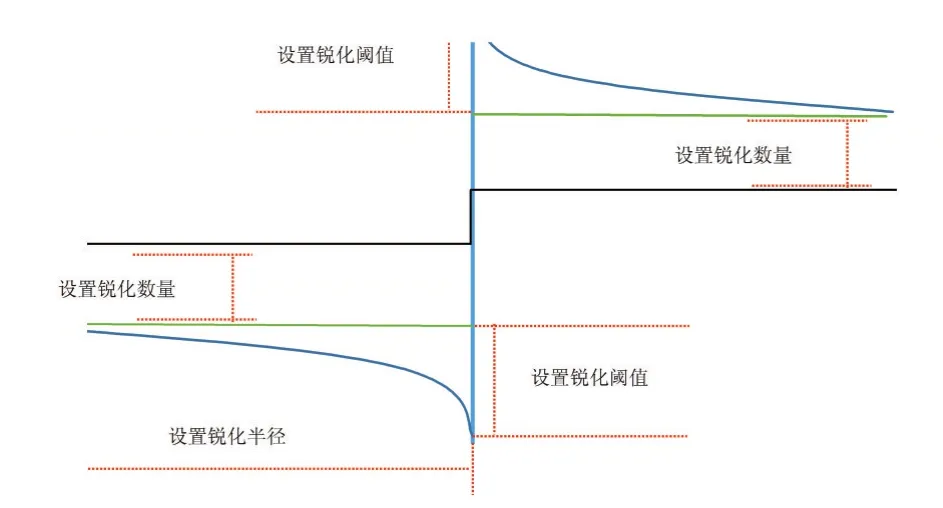
圖1 銳化原理示意圖

本文設計的銳化只針對圖像的高頻部分，其高頻濾波流程如圖2所示。

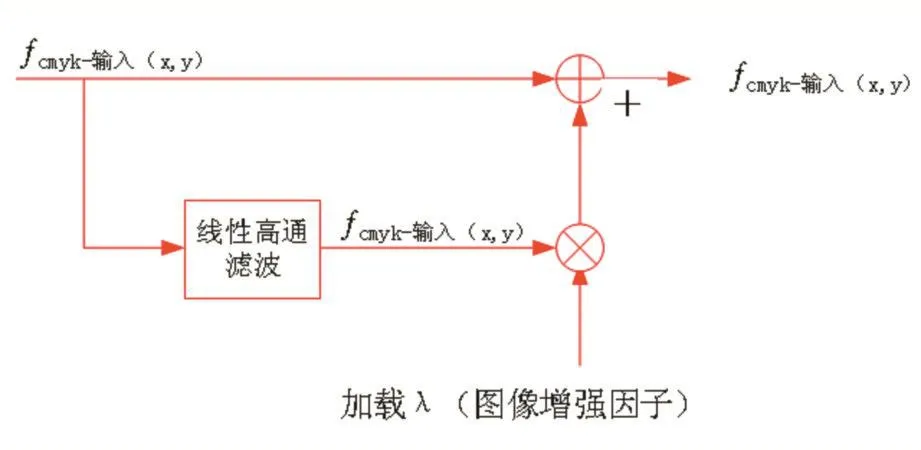
圖2 高頻濾波流程

銳化實現的算法公式為：

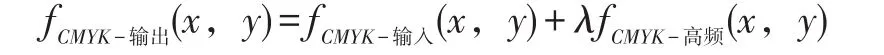
在上式中， fCMYK-輸入(x，y)為原 稿圖 像 ，fCMYK-高頻(x，y)為原稿經過低、中頻濾波后得到高頻圖像，λ為圖像增強的縮放因子，用于增強圖像邊緣像素的范圍，fCMYK-輸出(x，y)為銳化后圖像。

銳化轉換模板為：

提取圖像高頻部分的邊緣信息需要使用高通濾波器。其實現過程有兩步：一是圖像的傅立葉變換，二是建立高通濾波轉移函數。圖像的傅立葉變換公式為：

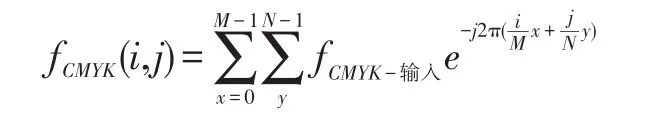
圖像高通濾波轉移函數公式如下：

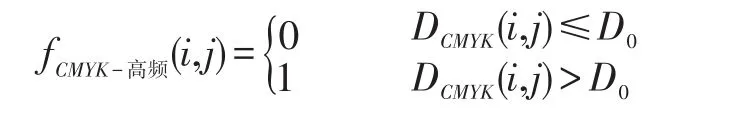
公式中，fCMYK-高頻(i,j)為0時，表示高頻通過的圖像細節，fCMYK-高頻(i,j)為1時，表示高頻阻止的圖像細節；D0為銳化半徑，也就是圖像高頻部分的信息；DCMYK(i,j)為圖像中被檢測的全部區域。

本文設計的圖像銳化模塊主要工作流程為：輸入圖像→進行傅里葉變換→創建高通濾波器→定義銳化半徑→設置銳化閾值→創建圖像CMYK四色獨立通道→在濾波器分離四色通道→加載銳化增強因子→與原始圖像點乘疊加→進行傅里葉逆變換→調用銳化變換模板→圖像通道合并→顯示、存儲結果圖像。

1. 3 圖像銳化質量評價設計

圖像均方誤差、峰值信噪比、結構相似度三個參數可以全面、準確地對圖像銳化質量進行評價，其中，圖像均方誤差與峰值信噪比為組合參數。

（1）均方誤差與峰值信噪比

均方誤差可以簡單方便地描述圖像的數據信息變化情況，定義：E為均方誤差值（為求和平均誤差），fCMYK-1(x,y)為原始圖像像素的灰度值，fCMYK-2(x,y)為銳化后圖像像素的灰度值，M為圖像縱向像素個數，N為圖像橫向像素個數。E值計算公式如下：

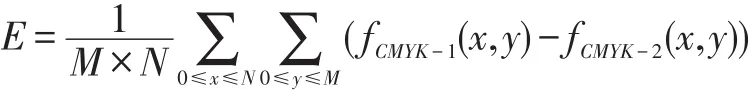
（2）峰值信噪比

峰值信噪比是使用最廣泛使用的圖像銳化質量評價參數，定義：P為峰值信噪比，L1為原始圖像像素最亮值，通常取值為255，L2為銳化圖像像素最亮值，通常取值也為255。P值計算公式如下：

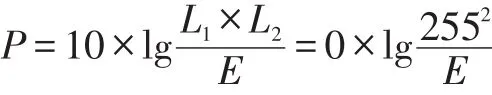
（3）圖像結構相似度

圖像結構相似度定義：LCSCMYK(x,y)為圖像的整體結構相似值，LCMYK(x,y)為圖像亮度相似值，CCMYK(x,y)為圖像對比度相似值，SCMYK(x,y)為圖像階調結構分布相似值。

LCMYK(x,y)=，I(x)、I(y)分別為橫、縱方向圖像像素灰度平均值，α為常數，α=(Kα×Lmax)2，Kα≤1，Lmax=255為圖像像素最亮值。

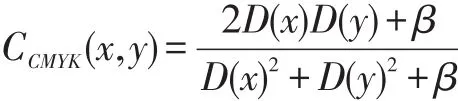
其中，D(x)、D(y)為圖像方差，β為常數，β=(Kβ×Lmax)2，Kβ≤1，Lmax=255為圖像像素最亮值。

SCMYK(x,y)=，其中，D(x,y)為圖像的協方差，D(x)、D(y)分別為圖像的方差，γ為常數，

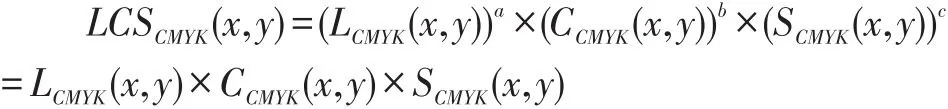
其中，a、b、c分別為LCMYK(x,y)、CCMYK(x,y)、SCMYK(x,y)的控制因子，通常情況下，a=b=c=1。

2 實驗及分析

2. 1 實驗方案

本文實驗方法采用比較法，使用拉普拉斯微分算法、Photoshop圖像USM銳化算法和本文設計的銳化算法三種算法對圖像進行銳化處理，將圖像均方誤差、峰值信噪比和結構相似度三個參數作為圖像銳化質量評價參數。其實驗方案如下：

（1）選擇一幅原稿實驗圖像。

圖3 圖像原稿

（2）使用MATLAB設計拉普拉斯微分銳化算法程序。

（3）使用MATLAB銳化算法進行銳化并提取邊緣輪廓圖。

（4）使用MATLAB設計本文提出的印前圖像銳化算法。

（5）使用圖像銳化質量評價系統完成圖像銳化效果的評判。

（6）對獲取的圖像邊緣輪廓圖和質量評價參數進行比較分析。

2. 2 數據與分析

實驗所需獲取的主要數據包括：采用三種方式實現圖像銳化后的邊緣輪廓圖、均方誤差E值、峰值信噪比P值和結構相似度LCS值。相關數據如圖5和表1所示。

根據實驗方案，實驗所需獲取的主要數據包括：采用三種方式實現圖像銳化后的邊緣輪廓圖、均方誤差E值、峰值信噪比P值和結構相似度LCS值，由于實驗圖像為CMYK模式，因此，將對C、M、Y、K四個分量的相關質量評價參數進行統計分析。相關數據如圖4和表1所示。

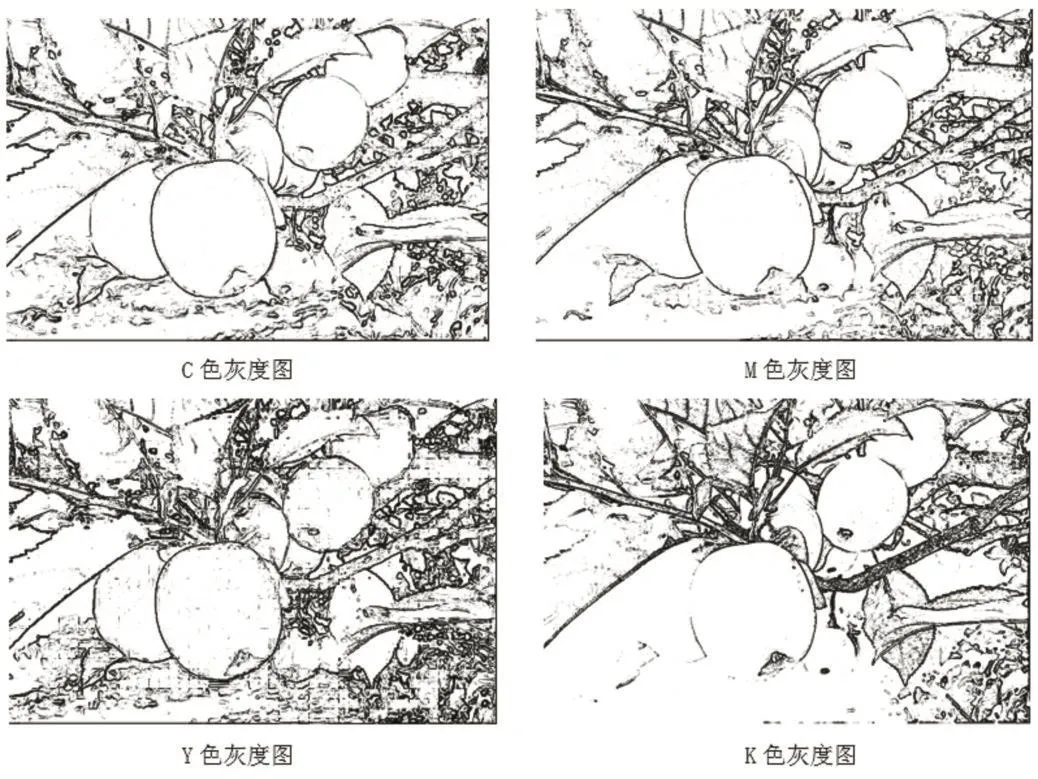
圖4 本文銳化算法邊緣輪廓圖

（1）邊緣輪廓分析

灰度圖像Lab值中的a值和b值都應為0，只有L值發生變化。在圖像中，0≤L≤100，L=0時說明圖像對應的像素點有信息，且為最深的黑色，L=100時，說明圖像對應的像素點沒有信息，也就是白色。邊緣輪廓圖中組成的全部像素點都滿足L=0，則由此像素點組成的線條也最清晰。

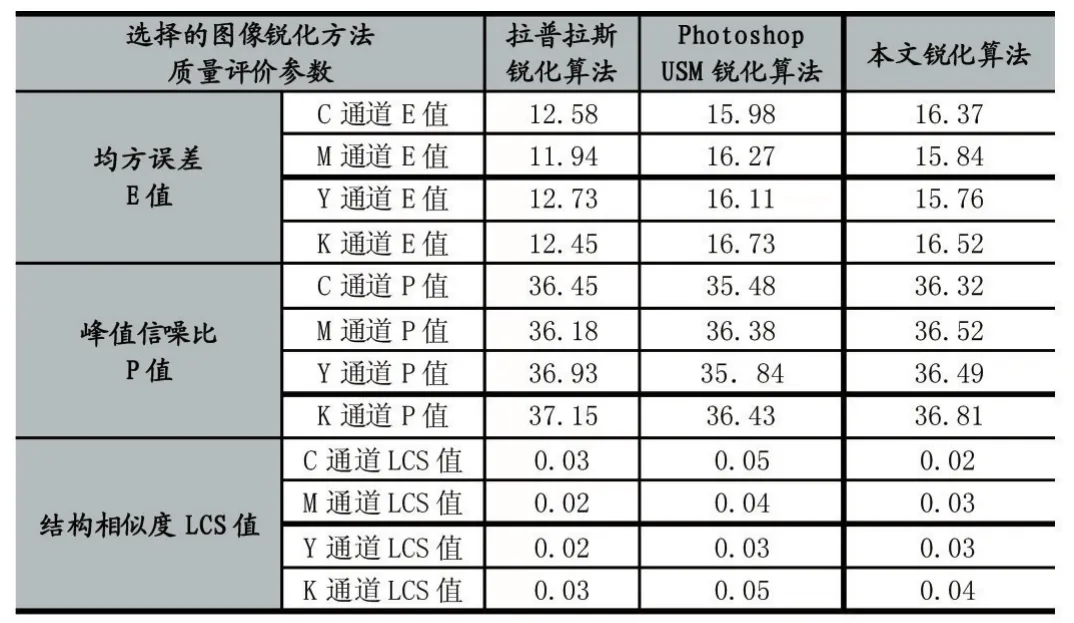
表1 三種銳化算法質量評價參數統計表

實驗選擇的圖像在銳化時產生的效果較為明顯，其中，拉普拉斯銳化提取到了一些階調變化復雜區域的邊緣輪廓信息，圖像中明顯的線條邊界L值不完全為0，清晰度在三種方法中不是最好的；Photoshop的USM銳化提取到的階調變化復雜區域的邊緣輪廓信息最多，但明顯的線條邊界L值不完全為0，清晰度和銳化作用范圍都比較理想；本文設計的銳化算法提取到了一些階調變化復雜區域的邊緣輪廓信息最少，圖像中明顯的線條邊界L值大多為0，邊界線條最清晰，但圖像整體清晰度不能說是最好的。

（2）質量評價參數分析

圖像銳化質量評價需要對數據進行客觀衡量標準比較，其中，E值越小圖像銳化效果越好，P值越大圖像銳化效果越好，相似度LCS值偏大圖像銳化效果越好。本文設計的銳化算法稍好于Photoshop的USM銳化算法，拉普拉斯銳化算法稍差。

3 結語

本文通過對圖像增強技術的理論學習，完成了一個以二階微分圖像邊緣檢測銳化為理論基礎的銳化功能模塊設計，并應用于了數字圖像處理過程中。本文設計的銳化算法可以通過銳化參量的控制，實現對不同原稿和不同印刷要求的需要，提高印刷圖像的清晰度。