基于雙線性插值的印刷圖像旋轉算法實現

李承軒，舒忠

（荊楚理工學院，荊門448000）

0 引言

印刷圖像旋轉操作，主要用于印刷頁面的排版設計。在當前的排版軟件中，圖像旋轉算法多為采用三次卷積算法對旋轉后的圖像進行插值補償。而對于印刷圖像后續進行RIP輸出操作，由于使用了計算量較大的算法，會導致輸出時速度降低。

在數字圖像處理中，對圖像進行旋轉操作，圖像占用的空間位置必定會變大[1]。這是導致印刷圖像在RIP輸出時運行速度降低的主要原因。圖像旋轉基本運算過程包括：矩陣旋轉→前向映射→反向映射（包括圖像插值運算）三個主要步驟[2]。圖像旋轉需要對其過程進行描述，并不只對旋轉結果進行運算，圖像旋轉的過程中，圖像占用空間的面積隨時都在發生變化，運算過程對此都進行了統計，這是圖像旋轉運算時需要大量空間的主要原因。同樣，圖像的平移算法也需要對圖像平移過程中圖像占用空間的面積進行統計，如果排版頁面不能提供足夠的運算占用空間，也是無法將圖像移動到需要地位置，特別是整個排版區域的邊緣位置。

圖像旋轉的數學運算實現是以圖像的中點為原點，圍繞原點對圖像進行一定角度的旋轉[3-5]。其變換的MATLAB實現流程為：讀取圖像→構建圖像矩陣且對矩陣進行初始化（初始值設為0，表示為黑色）→設置該圖像的旋轉角度（如：α=-15*3.1415926/180.0，表示為逆時針旋轉15°）→定義旋轉變換矩陣（H=[cos（α）-sin（α）0;sin（α）cos（α）0;0 0 1]）→使用矩陣乘法計算旋轉坐標的位置（雙循環計算旋轉圖像的每一個像素位置）→給旋轉后的每個像素進行賦值。

三次卷積插值是依據三次多項式S（x）計算最佳插值函數 sin（x）/x，其像素（x,y）的灰度值由其周圍 16 個像素點的灰度值加權后獲取[3]。三次卷積插值的MATLAB實現流程為：讀圖→轉雙精度浮點數據類型→構建圖像矩陣并對矩陣進行初始化→設置旋轉（或放大）參數→循環歷遍所有空間像素點為灰度插值運算結果賦灰度值做準備→計算u、v值（指需要賦灰度值像素點與相鄰像素點的橫向和縱向距離）并確定起始像素點（指16個相鄰像素中的第1個）的位置→循環計算相鄰像素點（共16個）的插值系數→計算16個相鄰像素點乘以插值系數后的灰度值和，并賦值于該像素點→使用同樣的計算方法完成圖像所有像素點的賦值→顯示結果。

根據印刷圖像處理的特點，在實際應用中，圖像旋轉后的插值補償，根本沒有必要使用三次卷積插值運算，使用雙線性插值運算所產生的圖像像素灰度值誤差進行補償，完全能夠滿足印刷圖像輸出的需要。本文在后面的內容中，將對其原因進行分析。

1 改進的圖像旋轉雙線性插值算法實現

1. 1 算法思想

本文設計的改進算法主要思想是：在變換域中完成圖像的旋轉與插值運算。

使用變換域（頻域）完成圖像旋轉與插值運算，可以減輕圖像處理過程中的復雜度和計算量。傅里葉變換是最基礎的頻域變換，其他多數頻域變換都是由傅里葉變換演化而來，例如：余弦變換和小波變換等。離散余弦變換，取的是傅里葉變換變換的余弦運算部分（復數的實部），而小波變換則是利用了短時傅立葉變換的原理，通過分窗實現頻域變換[3]。通過對幾個頻域變換方法的比較，充分考慮運算效率和運算結果等因素，選擇余弦變換為最佳頻域變換方式。

圖像旋轉屬于基本的圖像幾何變換，通常在空域中完成。本文設計采用一體化解決方案，選擇在頻域完成對圖像的旋轉與插值運算。

對圖像旋轉后的插值運算采用雙線性插值方式。本文研究主要是解決印刷圖像的處理，印刷圖像是通過4色油墨實現對圖像的復制，與圖像原稿相比，其印刷結果永遠追求的是接近原稿，很難實現超越原稿。從成像方式上看，數字圖像由可見光組成，產生的顏色千變萬化，而大多印刷只使用4色油墨去還原數字圖像的色彩，本身就有一定的難度。因此，圖像處理的過程，只要在質量控制的要求范圍內，可以對處理要求進行適當的調整。在進行圖像旋轉時，使用雙線性插值方式進行灰度值補償，可以滿足圖像對印刷的要求。

1. 2 算法實現

本文設計提出的算法實現步驟：

（1）圖像預處理：讀取圖像；轉雙精度浮點數據類型，以便于計算機實現在[0,1]以內的計算；將圖像轉換為矩陣表示等。如果原始圖像還需要進行其他增強處理，可以在空域內完成相應的變換。

（2）空域轉頻域：將空域表示的圖像轉換為離散余弦頻域表示，使用前文設計的離散余弦正變換函數完成。

（3）圖像旋轉：完成設置圖像的旋轉角度、定義旋轉變換矩陣、使用矩陣乘法計算旋轉坐標位置、旋轉后的每個像素賦值等操作。

（4）圖像插值：循環歷遍所有空間像素點、計算u、v值（需要運算的像素點與相相鄰像素點之間的橫向和縱向距離）并確定起始像素點（指4個相鄰像素中的第1個）的位置、使用計算公式完成灰度值計算并對所有像素點賦灰度值等操作。

（5）余弦逆變換：使用MATLAB提供的idct2（）函數完成圖像從頻域向空域的轉換。

（6）顯示運算結果：使用MATLAB中的imshow（）函數顯示進行變換后的結果。

其中：

對于雙線性插值計算，將選取4個鄰域像素點進行賦值的計算模板。雙線性插值的MATLAB實現流程為：讀圖→構建圖像矩陣并對矩陣進行初始化→設置旋轉（或放大）參數→循環歷遍所有空間像素點為灰度插值運算結果賦灰度值做準備→計算u、v值（需要運算的像素點與相相鄰像素點之間的橫向和縱向距離）并確定起始像素點（指4個相鄰像素中的第1個）的位置→使用計算公式完成灰度值計算并對所有像素點賦灰度值→顯示結果。

另外，對圖像進行旋轉有兩種方式：一種是以坐標系為基準的圖像旋轉，另一種是按圖像中點為基準的旋轉。本文采用以圖像中點為基準進行旋轉，在進行旋轉前，先將標準的平面坐標（平面坐標1，原點為圖像左上角像素點）轉換為圖像中點平面坐標（平面坐標2，原點為圖像中心像素點），然后進行圖像旋轉和插值計算，完成計算后再返回標準平面坐標中表示該圖像。

算法的核心MATLAB代碼如下：

……

T1=size（M,N,RGB）;%將圖像轉換為M×N的矩陣表示，圖像模式為RGB。

M1=round（m*abs（cos（JD））+n*abs（sin（JD）））;%計算圖像旋轉后的行數，JD為旋轉角度，round為四舍五入取整后的計算結果的MATLAB函數，abs為取絕對值后的計算結果的MATLAB函數。

N1=round（m*abs（sin（JD））+n*abs（cos（JD）））;%計算圖像旋轉后的列數，round為四舍五入取整后的計算結果的MATLAB函數，abs為取絕對值后的計算結果的MATLAB函數。

T2=zeros[M1,N1,RGB];%定義旋轉插值后的輸出圖像矩陣，并且矩陣中所有像素值為初始值0。

ZB1=[1 0 0;0-1 0;-0.5*N1 0.5*M1 1];%定義平面坐標1向平面坐標2轉換的運算系數矩陣ZB1。

ZB2=[1 0 0;0-1 0;0.5*c 0.5*r 1];%定義平面坐標2向平面坐標1轉換的運算系數矩陣ZB2。

K1=[cos（JD）-sin（JD）0;sin（JD）cosd（JD）0;0 0 1];%定義圖像旋轉的變換矩陣K1。

K2（i,j,:）=（1-u）*（1-v）*T1（i,j,:）+u*（1-v）*T1（i,j+1,:）+（1-u）*v*T1（i+1,j,:）+u*v*T1（i+1,j+1,:）;%進行插值運算，定義圖像插值運算的變換矩陣K2。其中，在圖像轉換為雙精度浮點數據類型后，i、j分別為像素點橫向坐標和像素點縱向坐標的整數部分，u、v分別為像素點橫向坐標和像素點縱向坐標的小數部分。注意：在需要將圖像轉換為雙精度浮點數據類型進行處理時，在頻域完成相應的處理不僅可以大大降低處理的復雜度，還可以提高運算速度。

T2=[i j 1]*ZB1*K1*K2*ZB2;%此為主體變換公式，對原始圖像依次進行平面坐標1向平面坐標2轉換、旋轉變換、插值運算和平面坐標2向平面坐標1轉換（注意是依次），將運算結果圖像的矩陣定義T2。

可以在K2和T2的計算過程中，使用離散余弦變換。

……

2 仿真實驗與結果分析

2. 1 實驗方法及目標

通過對方正飛騰（選用的一種國產排版軟件，用于比較分析）中的旋轉插值算法進行仿真，與本文設計的仿真算法進行比較，驗證本文設計的算法與方正飛騰旋轉插值算法結果相近，但本文設計的算法運算量小。對實驗結果的評價以客觀評價為主，采用峰值信噪比作為比較參數[6]。由于本實驗驗證的是低層次算法挑戰高層次算法的結果，因此，實驗結果方面，只求接近，不求超越，但在算法運算復雜度和運算量方面，要求占有絕對優勢。

2. 2 實驗過程

通過對實驗圖像進行測試，使用本本文提出的圖像旋轉方法得到的變換后的圖像如圖1所示，圖像旋轉角度分別為-30°和-90°。使用方正飛騰的圖像旋轉方法（其圖像旋轉是在二維離散傅里葉頻域采用三次卷積插值實現）的變換后的圖像如圖2所示，圖像旋轉角度也分別為-30°和-90°。

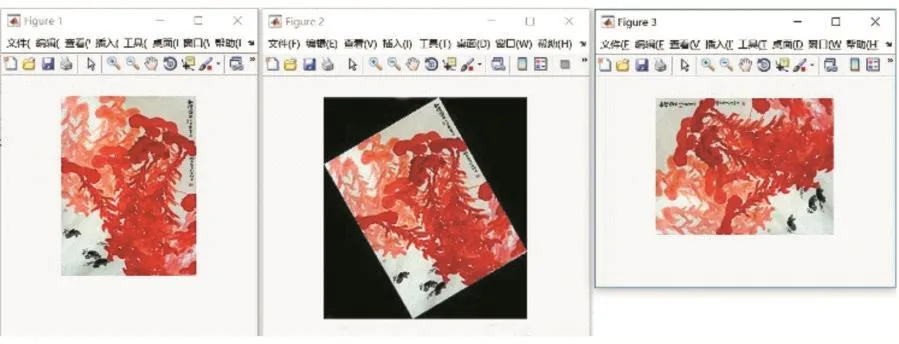
圖1 本文設計的圖像旋轉插值算法測試結果

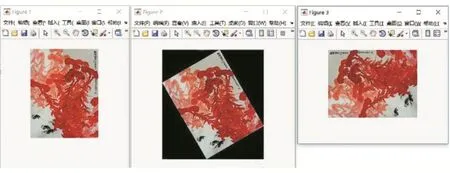
圖2 方正飛騰的圖像旋轉插值算法仿真測試結果

2. 3 客觀評價結果

兩幅圖像峰值信噪比計算的MATLAB實現流程為：讀取圖像→圖像轉為雙精度浮點數據類型表示→分離R、G、B三色通道，每個通道都視為單個灰度圖像→計算兩幅圖像各通道的灰度均值差→所有通道圖像轉換為矩陣表示→計算兩幅圖像R、G、B三色通道的峰值信噪比→取兩幅圖像的R、G、B三色通道峰值信噪比的平均值為兩幅圖像進行比較的峰值信噪比。

對兩種方法分別進行-30°和-90°測試的結果如圖3、圖 4所示。

圖3 使用兩種方法旋轉-30°進行測試的結果

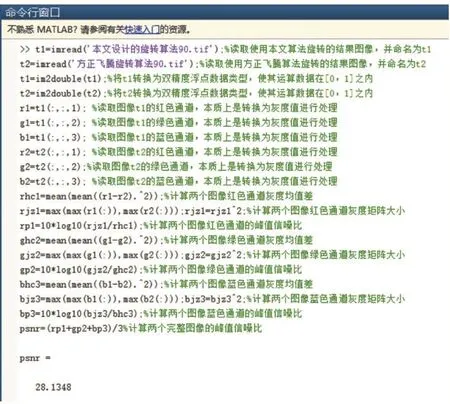
圖4 使用兩種方法旋轉-90°進行測試的結果

2. 4 實驗分析

實驗中使用的兩種旋轉插值算法的主要區別在于：方正飛騰的圖像旋轉插值算法使用的頻域轉換平臺為二維離散傅里葉變換，使用的插值方式為三次卷積插值；本文設計的圖像旋轉插值算法使用的頻域轉換平臺為二維離散余弦變換，使用的插值方式為雙線性插值。

二維離散傅里葉變換[7]的關鍵在于對復數進行計算，圖像通過在復數平面內進行表示，對復數的實部與虛部進行運算，其基本函數為：ck[i]=cos（2πki/N），sk[i]=sin（2πki/N），ck[j]=cos（2πkj/N），sk[j]=sin（2πkj/N），通過歐拉等式進行變換后的復數的形式：

cos（x）=1/2ej（-x）+1/2ejx（復數實部）

sin（x）=j（1/2ej（-x）-1/2ejx）（復數虛部）

cos（y）=1/2ej（-y）+1/2ejy（復數實部）

sin（y）=j（1/2ej（-y）-1/2ejy）（復數虛部）

在以上基本上，最終形成二維離散傅里葉變換。

而二維離散余弦變換[8]則只需要進行二維離散傅里葉變換中的復數實部運算，因此，二維離散余弦變換的運算量是二維離散傅里葉變換一半，因此，本文提出的圖像旋轉插值方法，在計算復雜度和計算量上具有較強的優勢。

根據前文論述，雙線性插值選擇了運算像素點周圍的4個像素點作為參考值，進行補償運算，而三次卷積插值則選擇了運算像素點周圍的16個像素點作為參考值，并使用卷積補償運算。因此，本文提出的圖像旋轉雙線性插值方法，同樣在計算復雜度和計算量上具有較強的優勢。

本次實驗收集的數據主要是將兩個圖像的峰值信噪比作為客觀比較的分析參數，兩幅圖像的峰值信噪比越高，說明兩者的相似度越大，且標準衡量值在30dB左右。通常情況下，峰值信噪比主要用于一幅圖像處理前后的對比，用于評價圖像的相似度。在對一幅圖像的處理前后進行比較時，相似度不高，才能說明圖像處理的結果越明顯，是圖像處理的理想取值。但是，本實驗是為了比較兩種圖像旋轉后的結果是否相近，因此，其峰值信噪比理想取值是越高越好。通過與標準衡量值在30dB相比，采用方正排版軟件的旋轉插值和本文設計的旋轉插值算法，在旋轉-30°和-90°時，其結果都接近標準衡量值，且旋轉-30°的結果要好于旋轉-90°的結果。因此，研究結果與目標要求基本一致。此項實驗結果獲取的客觀數據說明本文設計的旋轉插值算法有效。

3 結語

本文設計的印刷排版圖像旋轉改進仿真算法，主要解決了印刷圖像在制版輸出時的速度緩慢問題，解決問題的關鍵來自兩個方面：一是使用離散余弦變換替換廣泛使用的離散傅里葉變換作為變換平臺；二是使用雙線性插值算法替換三次卷積插值。另外，在圖像旋轉時，使用以圖像中點為基準進行旋轉。以上這些改進手段的使用，大大降低了運算量。通過選用國內常用的方正飛騰排版軟件與本文提出的算法進行仿真實驗表明，本文提出的算法在大大減少了運行時間的同時，圖像旋轉效果與方正飛騰排版軟件處理結果相近。