信息不完備下的知識遺忘

文習明

（廣東行政學院信息技術教研部，廣州510053）

0 引言

人類不僅具備不斷學習知識的能力，還具備策略性遺忘知識的能力。遺忘不僅僅意味著記憶的遺失，也是一個幫助大腦吸收新知識并有效做出決策的積極過程。隨著深度學習等一系列機器學習算法的不斷完善，智能體逐漸具備了學習知識的能力。如何讓智能體像人一樣具備知識遺忘的能力，目前仍然是人工智能所面臨的最大挑戰之一。

遺忘在人工智能領域扮演著十分重要的角色，在基于統計的機器學習領域和基于符號邏輯的知識表示與推理領域都對遺忘展開了研究。在機器學習領域，長短期記憶網絡（Long Short Term Memory Networks，LSTM）[1]、彈性權重固化（Elastic Weight Consolidation，EWS）[2]和瓶頸理論（Bottleneck Theory）[3]都試圖在記憶與遺忘之間取得平衡。在知識表示與推理領域、命題邏輯、一階謂詞邏輯、模態邏輯、描述邏輯、回答集邏輯程序設計（Answer Set Programming，ASP），以及情景演算（Situation Calculus）等多種邏輯語言中都有關于遺忘的研究。其被廣泛應用于最弱充分條件和最強必要條件的計算[4]、溯因推理[4]、相關性分析[5]、知識和信念的推理[6]、沖突解決[7]、本體分析與重用[8]、信息隱藏[8]、邏輯差異的判定[9]、知識庫更新[10]、ASP中的非單調推理[11]等諸多領域。

在知識表示與推理領域，遺忘（Forgetting）的思想最早可以追溯到1854年Boole提出的“消去（Elimination）”[12]。其直觀含義是：從當前理論中消除某些信息，得到一個比原理論更弱的新理論，但在保留下來的信息范圍內，新理論和原理論能夠推導出一致的邏輯結論。關于遺忘的理論研究，主要集中在兩個方面：可定義性問題和遺忘結果的計算問題。前者研究當前理論用某種邏輯語言表示時，遺忘結果是否依然能用該邏輯語言表示；后者研究如何計算遺忘之后所得的新理論。

信息不完備（Information Incompleteness）或信息不確定（Information Uncertainty）是人工智能現實應用場景中普遍存在的問題[13]，因此信息不完備條件下智能體知識的表示和推理一直是人工智能領域關注的熱點。現有研究方法大致分為兩類：一類采用概率的方式，貝葉斯網絡[14]是最有代表性的工作；一類是采用邏輯的方式，例如引入模態邏輯和謂詞邏輯。貝葉斯網絡雖然是目前不確定知識表達和推理領域最有效的理論模型之一，但其表達能力非常有限[13]。一階（謂詞）邏輯具有強的表達能力，通過引入個體變量和量詞，可以描述可能世界中的個體不確定，例如：“某人在房間里”，具體是哪個人不確定。模態邏輯通過引入模態詞可以描述可能世界的不確定，例如：“小娜可能在房間里”，但實際上小娜在不在房間不確定。模態謂詞邏輯是謂詞邏輯和模態邏輯結合的產物，它能描述上述兩種形式的不確定，適合更一般不確定知識的表示，例如：“可能有人在房間里”。因此，本文選擇模態謂詞邏輯為不確定知識的表示語言，對其中的知識遺忘展開研究。

我們將知識遺忘的定義擴展到模態謂詞邏輯，分析其基礎性質，并對其可定義性問題和計算問題展開研究。研究結果表明，一般情況下一階模態邏輯中知識遺忘是不可定義的。于是，我們識別出一階模態邏輯的一個片段，其表達能力較強，且從該片段的公式中遺忘原子命題是一階模態邏輯可定義的，遺忘謂詞是二階模態邏輯可定義的。該片段中公式的知識遺忘可以借助一階邏輯中公式的遺忘來計算。

1 基礎知識

本節介紹與本文研究相關的基礎知識和一些符號記法。

1. 1 模態謂詞邏輯語法與語義

模態謂詞邏輯是謂詞邏輯與模態邏輯結合的產物，我們參考文獻[15]給出一階模態邏輯（First Order Modal Logic，FOML）和二階模態邏輯（Second Order Modal Logic，SOML）的語法與語義。

為了給出FOML的語義，先定義論域不變模型（Constant Domain Model）M 和賦值（Assignment）v。

定義2：論域不變模型是一個四元組M=(W,R,D,π)，其中：

●W是非空的可能世界集合；

●R?W×W是W上的二元關系，即可能世界之間的可達關系；

●D是個體論域，即個體變量的取值范圍；

●是解釋函數，將任意可能世界w∈W解釋為論域為D的一階邏輯結構（Structure）π(w)。

簡單起見，本文采用論域不變模型，它是克里普克結構的擴展，要求不同可能世界中的個體論域相同。我們稱(M,w)為克里普克解釋，其中M=(W,R,D,π)是論域不變模型，w∈W稱為當前世界。

定義3：給定論域不變模型M=(W,R,D,π)，賦值v為每個個體變量x賦予個體論域D中的一個元素，即v:X→D，其中X是所有個體變量的集合。

給定d∈D，v[x/d]表示除了v[x/d](x)=d以外，其他變量賦值與v一致的賦值函數。

定義4：FOML的語義，由三元組(M,w,v)與公式φ之間的滿足關系給出，其中M=(W,R,D,π)是論域不變模型；w∈W，稱為當前世界；v是賦值。記為M,w,v?φ，其遞歸定義如下：

●M,w,v?φ∨φ 當 且 僅 當M,w,v?φ 或者M,w,v?φ；

●M,w,v??φ當且僅當M,w,v?φ；

●M,w,v??xφ 當 且 僅 當 存 在d∈D滿足M,w,v[x/d]?φ；

● M,w,v?Kφ 當且僅當對任意 w′∈W ，如果(w,w′)∈ R，則 (M,w′,v)?φ 。

若任意賦值v，均有M,w,v?φ，則M,w?φ。若任意M,w?φ均有M,w?φ，則φ?φ，稱公式φ是φ邏輯結論，或者說φ比φ邏輯上弱。若φ?φ且φ?φ，則φ≡φ。

SOML在FOML的基礎上引入了謂詞變量和二階存在量詞擴展而來。SOML記為。要給出SOML的語義，還需對謂詞變量賦值。因此引入謂詞內涵（Intension）的定義。

定義6：給定論域不變模型M=(W,R,D,π)，一個n元謂詞內涵I:W→(Dn)，賦予每個可能世界w∈W一個論域D上的n元關系I(w)。

在SOML中，一個謂詞變量在不同的可能世界中可以有不同的解釋。相應地，賦值的定義也擴展為v:X??→D?I，其中X是個體變量的集合，?是謂詞變量的集合，I是謂詞內涵的集合。v(x)∈D，若x∈X；v(P)∈I，若P∈?。即為個體變量x∈X賦值論域D中的一個元素，為謂詞變量P∈?賦值一個謂詞內涵。

定義7：SOML語義在FOML語義的基礎上，增加以下兩條遞歸規則構成：

● M,w,v??Pφ當且僅當存在一個內涵 I滿足M,w,v[P/I]?φ。

為簡單起見，本文僅考慮S5公理系統，即滿足如下公理（A1-A5）和推理規則（R1-R2）：

A1所有謂詞邏輯中的公理；A2 Kφ∧K(φ?φ)?Kφ ；A3Kφ?φ ；A4Kφ?KKφ ；A5?Kφ?K?Kφ；R1由?α和?α?β，可推導出?β；R2由?α，可推導出?Kα。

通過限定論域不變模型的可達關系為等價關系（自反、傳遞和對稱）即可滿足S5公理系統的要求。后續章節中不加說明的情況下，論域不變模型均為S5論域不變模型。

1. 2 謂詞邏輯中的遺忘

Lin和Reiter從模型論的角度定義了一階邏輯中的遺忘[5]，并得到如下結論。

命題1：令 μ 是原子命題 p(τ→)或謂詞 p，從一階邏輯公式 φ∈? 中遺忘 μ ，記為 forget(φ,μ)，則：

2 模態謂詞邏輯中的知識遺忘

本節我們定義一階模態謂詞邏輯中的知識遺忘，并分析其基本性質。令 μ是原子命題 p(τ→)或謂詞 p。

定義 8：給定克里普克解釋 (M,w)和 (M′,w′)，其中M=(W,R,D,π)和 M′=(W′,R′,D′,π′)，(M,w)和 (M′,w′)除了對 μ 的解釋之外互模擬，記為 (M,w)～μ(M′,w′)，如果D=D′且存在非空二元關系 ρ?W×W′，(w,w′)∈ρ。其中如果 (s,s′)∈ ρ，則滿足如下條件：

● π(s)～μπ′(s′)，即 M 對 s的解釋與 M′對 s′的解釋幾乎一致，除了對μ的解釋可能不同之外；

●對任意的 t∈W ，如果 (s,t)∈R，則必存在 t′∈W′使得 (s′,t′)∈ R′且 (t,t′)∈ ρ；

●對任意的 t′∈W′，如果 (s′,t′)∈R′，則必存在 t∈W使得 (s,t)∈R 且 (t,t′)∈ρ。

定義9：給定FOML公式φ∈?m，公式φ是從φ中遺忘 μ 之后的結果，記為 kforget(φ,μ)≡φ ，當且僅當，對任意的S5克里普克解釋(M,w)和賦值v，M,w,v?φ當且僅當存在 S5克里普克解釋 (M′,w′)，M′,w′,v?φ且 (M,w)～μ(M′,w′)。

定義10：給定公式φ，若存在公式φ滿足φ≡φ且φ中不包含μ，則稱公式φ與μ無關。

命 題2：給 定 φ∈?m，若kforget(φ,μ)≡φ ，則φ?φ；且對于任意與 μ無關的公式η，φ?η當且僅當φ?η。

命題2表明，一個理論（公式）知識遺忘之后所得的新理論（公式）在邏輯上比原理論（公式）弱，在與被遺忘對象無關的信息方面兩者保持邏輯一致。這正是遺忘的基本性質之一。

命題3：一階模態謂詞邏輯中知識遺忘滿足如下性質：

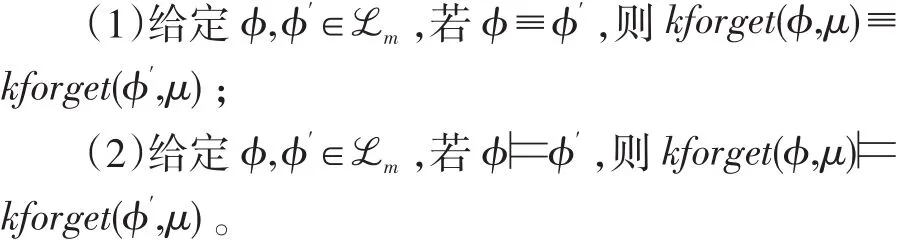
命題3表明，一階模態謂詞邏輯中知識遺忘保持邏輯強弱關系，即兩個理論在遺忘相同的對象后其結果之間的強弱關系保持不變。

命題4：一階模態謂詞邏輯中知識遺忘滿足如下性質：

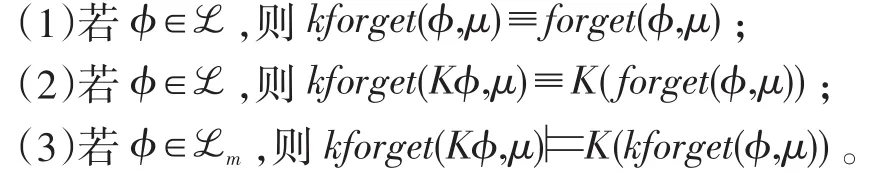
結論1表明，一階邏輯中的變量遺忘實質上是一階模態謂詞邏輯中知識遺忘的特例；結論2表明，當模態算子K轄域內是客觀公式時，知識遺忘與模態算子K之間滿足交換律；結論3表明，在一般情況下，知識遺忘與模態算子K之間并不滿足交換律，因為 K(kforget(φ,μ))?kforget(Kφ,μ)。

命題5：一階模態謂詞邏輯中知識遺忘滿足如下性質：

結論1表明，一階模態謂詞邏輯中知識遺忘對邏輯析取滿足分配律；結論2表明，一階模態謂詞邏輯中知識遺忘對邏輯合取并不滿足分配律，因為kforget(φ1,μ)∧kforget(φ2,μ)?kforget(φ1∧φ2,μ)；結論 3表明，一個一階模態謂詞邏輯理論（若干有限語句的集合）進行知識遺忘時，與被遺忘對象無關的語句保持不變。

命題6：一階模態謂詞邏輯中知識遺忘滿足如下性質：

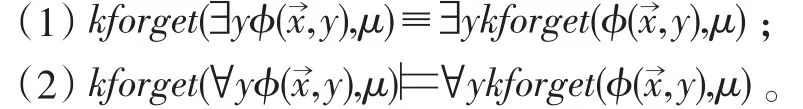
結論1表明，一階模態謂詞邏輯中知識遺忘與一階存在量化之間滿足交換律；結論2表明，一階模態謂詞邏輯中知識遺忘與一階全稱量化之間并不滿足交換律，因為 ?ykforget(φ(x→,y),μ)?kforget(?yφ(x→,y),μ)。

通過對基本性質的分析，我們對一階模態謂詞邏輯中知識遺忘有了更深的認知，同時也為研究其可定義性問題和計算問題提供了依據。

3 FOML中知識遺忘的可定義性與計算

由命題4可知，一階邏輯中的變量遺忘實質上是一階模態謂詞邏輯中知識遺忘的特例。由命題1可知，一階謂詞邏輯中的遺忘是不可定義的，即遺忘的結果需要二階謂詞邏輯才可表示。由此，可知一階模態謂詞邏輯中的遺忘也是不可定義的。本章識別出一階模態謂詞邏輯中的一些片段，其知識遺忘在可定義性和計算方面有較好的性質。

顯然，擴展項知識遺忘的結果依然是擴展項，即擴展項上的知識遺忘具有可定義性，且擴展項的知識遺忘可以借助一階邏輯的遺忘來計算。

定理1：如果φ是?-DNF范式，則其遺忘原子命題之后的結果是FOML可表示的；其遺忘謂詞之后的結果是SOML可表示的，且模態詞不會出現在二階量詞的轄域內。

定理1表明：我們尋找到了一階模態邏輯中的一個片段（即?-DNF范式），這個片段中的公式，遺忘原子命題之后的結果是FOML可表示的，遺忘謂詞之后的結果是SOML可表示的，且模態詞不會出現在二階量詞的轄域內。

FOML中經常被研究的另一個片段是模態詞不出現在量詞轄域內的公式（formula without quantifying-in）。例如：K?xφ(x)和 L?xφ(x)屬于該片段，其中φ(x)∈? 。但?xLφ(x)和?xKφ(x)不屬于該片段。

定理2：在S5一階模態邏輯中，任意模態詞不出現在量詞轄域內的公式φ，均存在一個公式φ∈?m，滿足φ≡φ且φ中不出現模態詞的嵌套。

證明：可以基于公式φ的模態詞的嵌套深度歸納證明。需利用等價轉換規則 K(α∧β)≡Kα∧Kβ和K(α∨σ)≡Kα∨σ，其中σ是主觀公式。

不出現模態詞的嵌套，即模態詞轄域內均是客觀公式。由此可知，該片段內的任意公式φ，均可等價轉換成形如 α1∨…∨αn的析取范式（DNF），其中 αi是形如 β1∧…∧βm的合取式，βi是客觀公式或者形如Kγ或Lγ的公式，其中γ是客觀公式。顯然，這樣的DNF是?-DNF的特例。因此，該片段內的公式知識遺忘也滿足定理1所描述的性質。

綜上所述，FOML中，滿足遺忘原子命題之后結果FOML可表示；遺忘謂詞之后結果SOML可表示，且模態詞不會出現在二階量詞轄域內的共有三個片段：

（1）客觀公式，即一階邏輯公式；

（2）模態詞不出現在量詞轄域內的公式；

（3）?-DNF范式公式。

顯然，片段1?片段2?片段3。即片段3是目前為止，我們找到的滿足上述知識遺忘性質的最大片段。下面，通過一些實例來進一步認識這些片段。例如：給定 φ(x)∈? ，?xKφ(x)和?xLφ(x)屬于片段 2，因為在 論 域 不 變 假 設 下 ， ?xKφ(x)≡K?xφ(x)，?xLφ(x)≡L?xφ(x)。 ?xKφ(x)，?xLφ(x)，?x?yLφ(x,y)，?x?yLφ(x,y)和 ?x?yKφ(x,y)均 屬 于 片 段3，其 中?x?yLφ(x,y)≡?xL?yφ(x,y),?x?yKφ(x,y)≡?xK?y[φ(x,y)]。注意：?x?yKφ(x,y)不屬于片段3。上述實例表明，?-DNF范式公式雖然只是FOML的一個片段，但其已具有了相當的表達能力。

4 結語

本文選擇模態謂詞邏輯為信息不完備情況下不確定知識的描述語言，對其知識遺忘推理問題展開研究。我們將知識遺忘的定義擴展到模態謂詞邏輯，分析其基礎性質，并對其可定義性問題和計算問題展開研究。研究結果表明，一般情況下一階模態邏輯中知識遺忘是不可定義的。因此，我們識別出一階模態邏輯的一個片段，其表達能力較強，且從該片段的公式中遺忘原子命題是一階模態邏輯可定義的，遺忘謂詞是二階模態邏輯可定義的，且模態詞不會出現在二階量詞轄域內。該片段中公式的知識遺忘可以借助一階邏輯中公式的遺忘來計算。未來，我們將考慮引入二階量詞消去技術，進一步尋找遺忘謂詞也是一階模態邏輯可定義的片段。