甘藍型油菜籽薄層熱風干燥的能耗分析與研究

胡眾歡，李守太，楊 亮，陳同浩，舒 雷，楊 玲，楊明金

(西南大學 工程技術學院/丘陵山區農業裝備重慶市重點實驗室，重慶 400715)

0 引言

干燥是通過熱能除去濕物料中水分過程[1]。大量的干燥方法隨著科技的迅速發展涌現而出，如真空冷凍干燥、紅外干燥、噴霧干燥等，但熱風干燥以其操作簡單、成本低、對環境及場地設備等要求不高的優點，長期占據著較大的市場份額[2]。目前，國內外學者對熱風干燥方法進行了諸多研究，并取得了大量成果。劉業鳳等人研究了真空冷凍干燥蒜丁的實際生產能耗問題[3]；楊大成等對傳導干燥和對流干燥的能耗進行了分析[4]；趙娜等基于LEAP(Long Range Energy Alternatives P1anning)方法對我國的糧食干燥系統進行了能耗評價[5]；董繼先等研究了蘋果片干燥過程中的能耗問題[6]；但其大都是基于干燥設備的額定功率進行分析，少有從干燥機理上對能耗進行評價，忽略了干燥機理的研究。為此，在前人研究的基礎上，基于物料干燥機理，構建了物料干燥過程中的能量消耗模型，旨在為物料干燥過程中的節能分析提供一定的理論依據和參考。

1 基礎理論

目前，對于物料干燥過程的宏觀表述多以多孔介質理論為基礎。多孔介質中的熱質傳遞是一種非常復雜的傳輸現象，其質量傳遞涉及液相流動、毛細流動、蒸汽流動、蒸汽擴散及液相擴散等諸多現象，在特定的干燥過程中，多種現象可能單一作用，也可能共同作用[7]；其能量傳遞包括熱傳導、對流換熱及熱輻射等。大量研究表明，對于顆粒直徑較小的多孔介質，其機體中的對流換熱過程可忽略不計，熱輻射現象在溫差不大的情況也可以忽略不計[8]。

根據不同的側重點，研究者先后提出了液態擴散理論、毛細理論、蒸發冷凝理論、Luikov理論、Philip與DeVries理論、Krischer和Berger等理論來描述干燥過程中的質量或熱質傳遞過程[9]。在此基礎上，結合流體力學、熱力學基礎方程，可建立干燥過程的控制方程組[10]，即

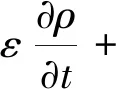
(1)

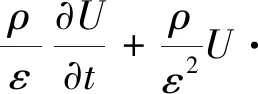
(2)

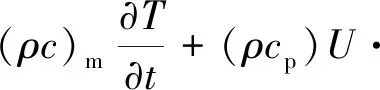
(3)

其中，方程(1)為質量傳遞過程中的連續性方程；方程(2)為動量方程；方程(3)為能量方程；ε為材料孔隙率(-)；ρ為密度(kg/m3)；U為速度(m/s)；F為體積力(N/m3)；p為壓力(Pa)；T為溫度(K)；c為比熱容(J/kg·K)；k為熱導率(W/m·K)；t為時間(s)。

2 能耗模型

以被干燥物料為研究對象，能量消耗由3部分組成：①濕分遷移過程中所獲取的動能；②物料升溫所吸收的熱量；③濕分蒸發所帶走的熱量。據此，根據熱力學第一定律可得：物料吸收熱量=物料升溫消耗熱量+濕分動能+濕分蒸發消耗熱量。

考慮到甘藍型油菜籽薄層熱風干燥實際干燥過程極為緩慢(即物料內濕分遷移速率非常小)，所以濕分遷移過程中所具有的濕分動能與其余兩項相比可忽略，故方程可簡化為如下形式：物料吸收熱量=物料升溫消耗熱量+濕分蒸發消耗熱量。現對此兩部分能量消耗進行詳細分析。

2.1 物料升溫消耗熱量

被干燥物料中含有固、液、氣三相，根據熱力學定理，則

dQs=cs·dms·dT

(4)

dQl=cl·dml·dT

(5)

dQg=cg·dmg·dT

(6)

其中，Q為熱量(J)；c為比熱容(J/kg·K)；m為質量(kg)；T為溫度(K)；下標s、l、g分別表示固、液、氣三相。

對方程(4)～(6)進行積分可得

(7)

2.2 濕分蒸發消耗熱量

濕分蒸發消耗熱量等于濕分蒸發量乘以水的蒸發熱，其微分表達式為

dQevap=λ·dmevap

(8)

其中，Qevap為水分蒸發所消耗熱量(J)；λ為蒸發熱(J/kg)；mevap為蒸發水的質量(kg)。

mevap可進一步寫成蒸發速率與時間的函數，即

mevap=mevap(vevap,t)

(9)

其中，vevap為干燥速率(kg/s)；t為干燥時間(s)。

在整個干燥過程中，干燥速率vevap是變量，所以采用方程(9)的微分形式進行計算，即

dmevap=vevapdt

(10)

蒸發速率可以由實驗直接確定。因為在干燥過程中，水分總是以水蒸氣的形式離開物料，故蒸發速率在數值上等于干燥速率。基于前述分析，本文將從實驗結果直接獲取干燥速率。

將方程(10)帶入方程(8)，并進行積分可得

(11)

綜上，整個干燥過程能量消耗總量為

Q=Qevap+∑Qi

(12)

其中，Q為干燥過程消耗總能量(J)。

2.3 溫度場的計算

溫度場計算依賴于方程(3)，根據第1節所述可忽略對流傳熱和熱輻射。方程(3)簡化為

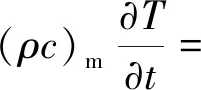
(13)

其中

(ρc)m=(1-ε) (ρc)s+ε(ρcp)

(14)

km=(1-ε)ks+εkl

(15)

(16)

本節建立了物料干燥過程的能耗模型，并詳細論述了模型中所需重要參數(蒸發速率、溫度場)的獲取與計算方法。由實驗測量數據獲取實際蒸發速率，并通過方程(13)求取溫度場，最后按照方程(12)計算干燥過程的總能耗。

3 數值求解與實驗驗證

本節在前述分析的基礎上，使用Comsol5.2a軟件對甘藍型油菜籽薄層熱風干燥過程中的能耗進行求解。

3.1 蒸發速率的獲取

根據2.2小節所述，蒸發速率在數值上等于干燥速率。楊玲等的研究結果表明：Page模型預測的甘藍型油菜籽薄層熱風干燥曲線與實驗所得干燥曲線一致性最好[11]，故本文選取Page模型對實驗數據進行擬合。Page模型的形式為

m=a·exp(-ktn)

(17)

其中，m為干燥過程中物料剩余總質量(g)；t為干燥時間(s)；a、k、n為模型參數。

通過數據分析軟件SPSS20.0對實驗數據進行擬合，結果如表1所示。

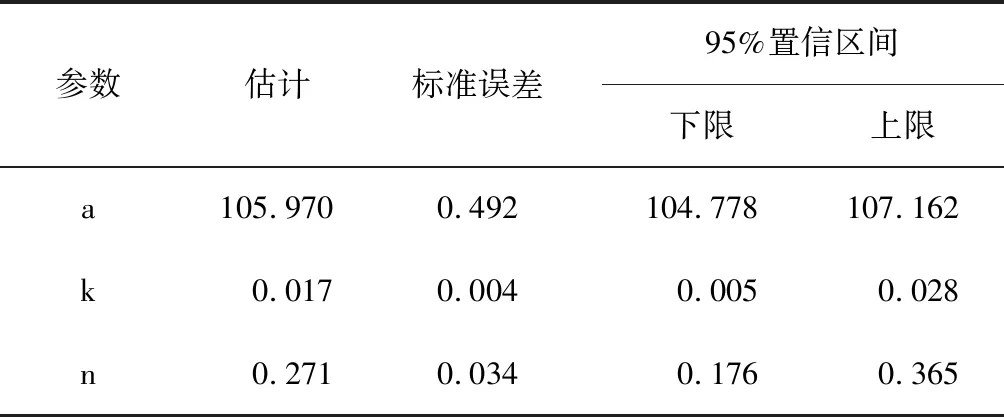
表1 參數擬合表

根據擬合結果，a=105.97，k=0.017，n=0.271。帶入方程(17)可得

m=105.97·exp(-0.017·t0.271)

(18)

對式(18)取導即可得到蒸發速率為

(19)

將蒸發速率嵌入方程(13)進行求解即可得到溫度場。

3.2 溫度場的求解

溫度場求解依賴于方程(13)，即

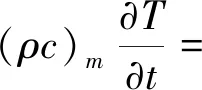
求解時，仍需要對方程進行一定調整和修改。熱風干燥過程的材料內部是不存在熱量源的，其濕分遷移所需能量均來自于外部熱風，故方程(13)中的源項q應略去；同時考慮到水蒸氣離開物料會帶走一定熱量(濕分蒸發所需熱量)，根據Datta所述，可將該部分熱量作為源項插入能量方程[12]，即將蒸發消耗能量作為源項插入方程(13)，故能量方程變為如下形式，即

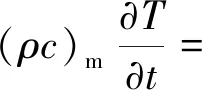
(20)

方程(20)即為求解溫度場所用的能量方程，使用comsol5.2a對方程(20)進行求解。所取甘藍型油菜籽的物性參數如表2[13-14]所示。

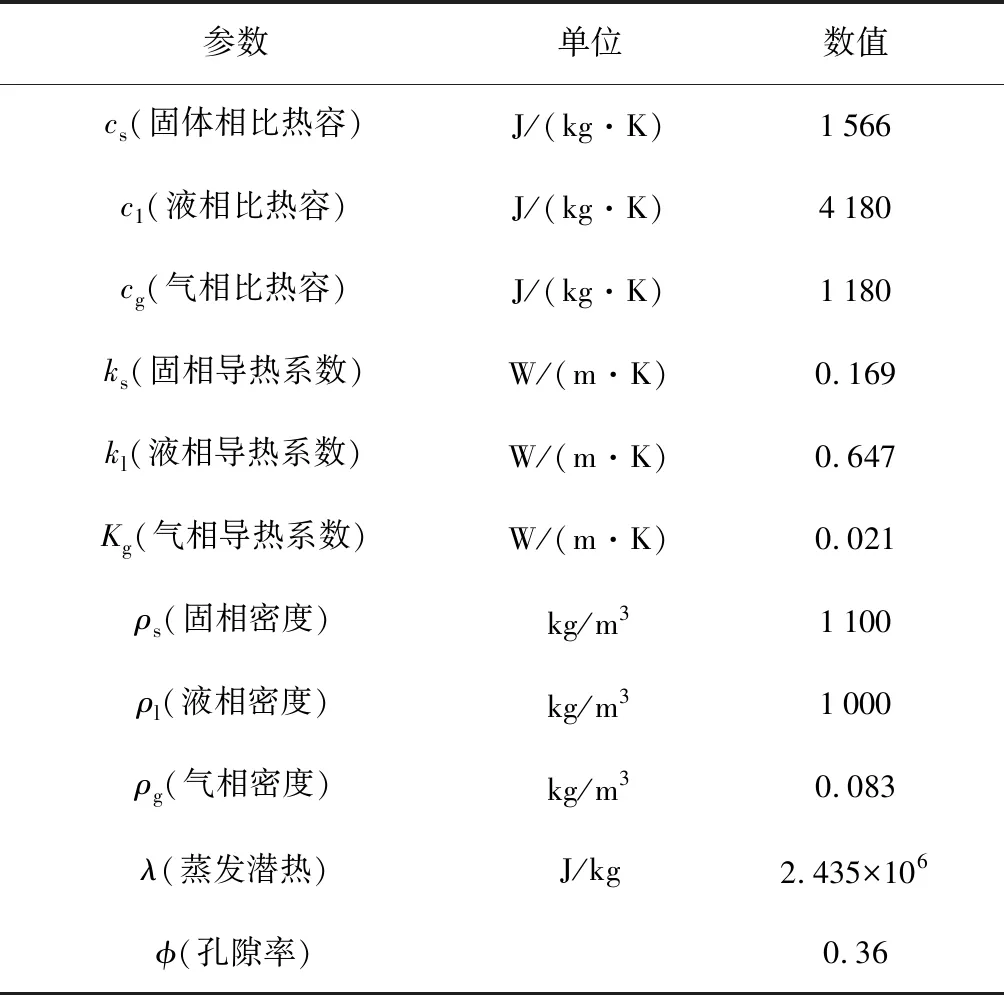
表2 參數取值

甘藍型油菜籽薄層熱風干燥過程的溫度場分布，如圖1(t=150s)、圖2(t=300s)和圖3(t=600s)所示。

分析圖1～圖3可知:隨著干燥時間的增加，物料內部溫度逐漸上升，最終趨近于熱風溫度(368.13K)，符合實際情況。

3.3 能耗的計算

按照方程(12)計算干燥過程能量消耗，干燥能量曲線如圖4所示。由圖4可知：隨著干燥時間的增加，物料的能量消耗越來越慢，與實際情況吻合。

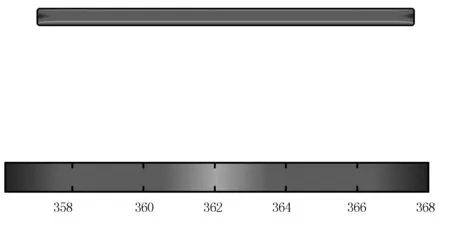
圖1 溫度矢量圖(150s)

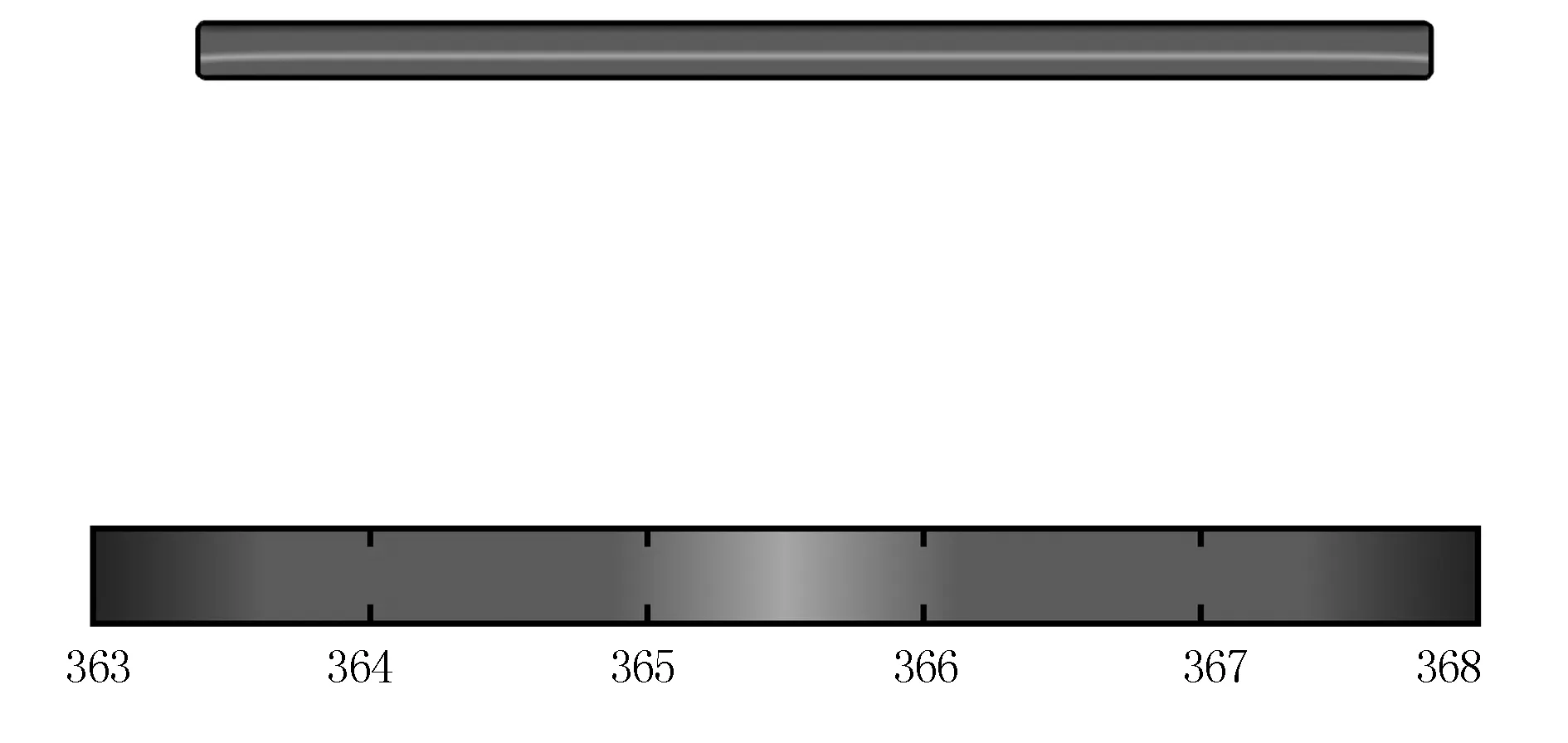
圖2 溫度矢量圖(300s)

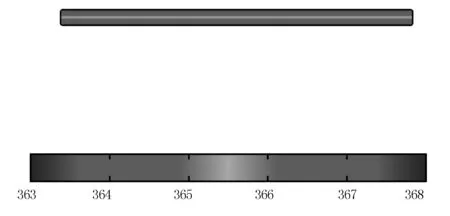
圖3 溫度矢量圖(600s)

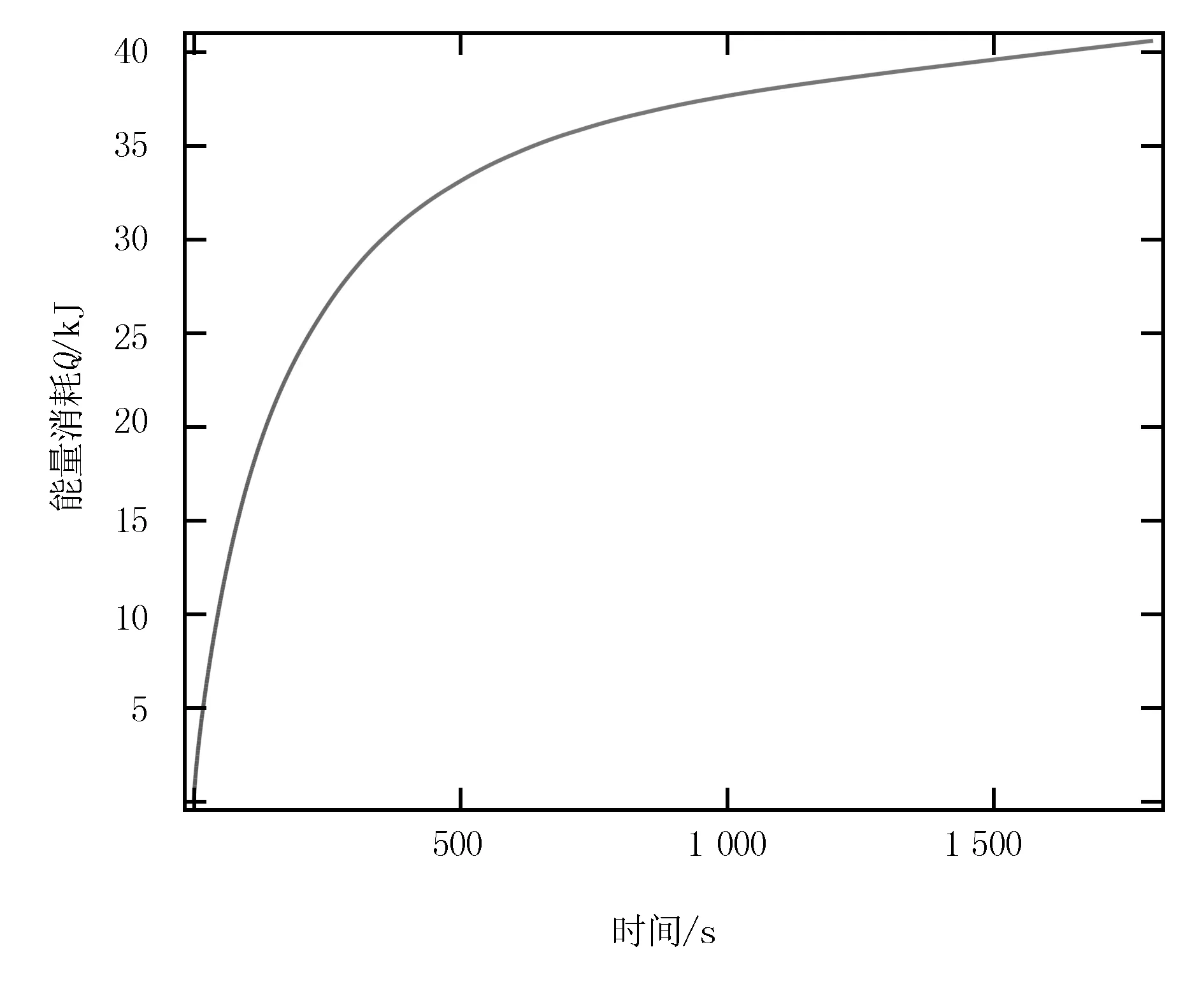
圖4 干燥能量曲線

3.4 求解結果驗證

由于物料在整個干燥過程中所消耗的能量無法直接測取，所以引入干燥活化能的概念來對比計算值與實驗值的差異。干燥活化能是指干燥過程中蒸發單位摩爾水分所需要的啟動能量[15]。

3.4.1 實驗值計算

本文按照吳青榮等人所述方法計算實驗值[16]。干燥時間取2h，計算結果為39.2kJ/mol。

3.4.2 模擬值計算

根據干燥活化能定義，則

(21)

其中，Ea為干燥活化能(J/mol)；E(t)為t時刻消耗的能量(J)；m(t)為t時刻干燥出的水分(mol)。

干燥時間取30min(1 800s)，計算值為42.802 5kJ/mol。與實驗結果相比，其相對誤差為9.19%。在實驗所允許的誤差范圍內，模擬結果是正確的。

4 結果與討論

本文敘述了甘藍型油菜籽薄層熱風干燥過程中能耗模型的構建及求解過程，并對其進行了驗證，結果顯示計算值與實驗值吻合得較好。

引入能量利用率的概念對干燥過程的經濟性做了進一步分析。能量利用率是指濕分蒸發所消耗的能量與干燥設備所消耗的能量的比值，即能量利用率=用于濕分蒸發的能量/干燥設備消耗的總能量。

假定干燥設備的功率為P，干燥操作時間為t，則其能量消耗為Pt，記能量消耗率為η，則

(22)

其中，Q為干燥過程中濕分蒸發所消耗的能量。

由式(12)計算，取功率P為單位1，根據式(22)可繪制能耗比曲線，如圖5所示。

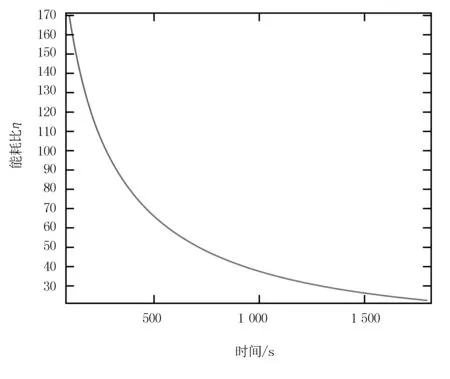
圖5 能耗比曲線

由圖5可知：隨著干燥時間的增加能耗比越來越低，最后趨近于0。在實際干燥過程中，干燥速率隨時間的增加呈下降趨勢。根據式(10)、式(11)可知：單位時間內排出的水分量越來越少，干燥過程所需實際能量越來越低，而干燥設備在固定條件下的功率是恒定的，即單位時間內所消耗的能量是固定值，故其比值(能耗比)越來越小。

從節能減排的角度考慮，整個干燥過程的能耗比越大越好，能耗比曲線越陡峭越好。因此，實際工藝中應該在在允許范圍內盡可能大地提高干燥速率，以縮短整個過程的干燥時間和能量消耗。