本期試卷參考答案

編者的話:同學們在演練的過程中,如果需要更為詳細的參考答案,請掃描右邊的二維碼,關注編輯部的官微“高中數學解題反思”,不但能獲悉詳細參考答案,還可以另辟蹊徑,開拓知識視野,學會解題反思!
三角函數綜合演練A卷參考答案與提示
一、選擇題
1.提示:應選A。 2.提示:應選B。3.提示:應選C。 4.提示:應選 C。 5.提示:應選C。 6.提示:應選B。 7.提示:應選A。 8.提示:應選D。 9.提示:應選D。
10.提示:應選A。 11.提示:應選B。12.提示:應選 A。 13.提示:應選C。14.提示:應選 A。 15.提示:應選 B。16.提示:應選 B。 17.提示:應選 C。18.提示:應選 C。 19.提示:應選 C。20.提示:應選 A。 21.提示:應選 D。22.提示:應選 B。 23.提示:應選 C。24.提示:應選A。
二、填空題
三、解答題
(2)因為Q(x0,y0)是線段 PA 的中點,點所以點P的坐標為因為點P 在函數y=的圖像上,且所
三角函數綜合演練B卷參考答案與提示
一、選擇題
1.提示:應選C。 2.提示:應選A。3.提示:應選 A。 4.提示:應選 A。 5.提示:應選 A。 6.提示:應選 D。 7.提示:應選A。 8.提示:應選C。 9.提示:應選C。10.提示:應選C。 11.提示:應選A。12.提示:應選C。 13.提示:應選 D。14.提示:應選 A。 15.提示:應選 B。16.提示:應選 C。 17.提示:應選 C。18.提示:應選 A。 19.提示:應選B。20.提示:應選B。 21.提示:應選D。
二、填空題
三、解答題
32.提示:(1)由函數f(x)的最大值是3,可得A+1=3,即A=2。因為函數圖像的相鄰兩條對稱軸之間的距離為所以最小正周期T=π,可得ω=2。
數據補全如表1所示。
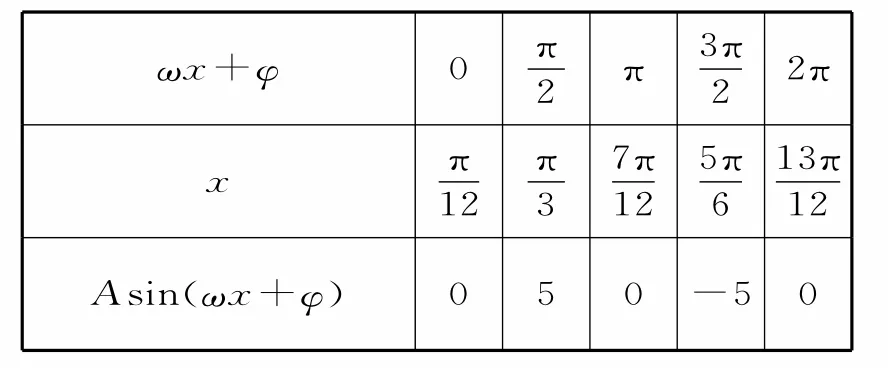
表1
(2)f(x)=2sin2x。將y=f(x)的圖像向左平移個單位,再向上平移1個單位后得到的圖像,即
易知函數圖像在一個周期內有3個零點。若b-a最小,則a和b都是零點,此時在區間[a,π+a],[a,2π+a],…,[a,mπ+a](m∈N*)上分別恰有3,5,…,2m+1個零點,所以在區間[a,14π+a]上恰有29個零點,從而在區間(14π+a,b]上至少有一個零點,所以另一方面,在區間上恰有30個零點,因此b-a的最小值為
38.提示:(1)當a=1時,f(x)=-cos2x
(2)依題意可得sin2x+acosx+a≤1,即sin2x+a(cosx+1)≤1對任意x∈恒成立。當時,0≤cosx≤1,則1≤cosx+1≤2,所以對任意恒成立。令t=cosx+1,則1≤t≤2,所以2對任意1≤t≤2恒成立,于是可得a≤因為當且僅當t=1,即時取等號,所以a≤0。
39.提示:(1)由點A(0,0),B(6,0),可得sinφ=0,即φ=0,且這時f(x)=因為(a+c)(sinC-sinA)=(a+b)sinB,所以(a+c)(c-a)=(a+b)b,整理可得即cosC=可得

