盤點三角函數最值問題的求法

■柯定尊

三角函數最值問題是近幾年高考考查的一個重點，三角函數最值是函數最值的一個重要組成部分，與二次函數、不等式等內容緊密相關，由于其題型的變化多樣，常常讓同學們感到無從下手。下面介紹幾種常見的求三角函數最值的方法，供同學們參考。

一、利用配方法求三角函數的最值

若函數表達式中只含正弦函數或余弦函數，且它們的次數是2時，一般需要通過配方或換元將給定的函數化歸為二次函數的最值問題來處理。

例1求函數y=-2sin2x+2sinx+1的最值。

解：函數y=-2sin2x+2sinx+1=因為-1≤sinx≤1，所以當sinx=-1，即時當即時，ymax=-2×0+

解答本題的關鍵是先將函數式進行配方，再轉化為二次函數求最值問題。

跟蹤練習1：函數y=cos2x-3cosx+2的最小值為（ ）。

提示：函數y=cos2x-3cosx+2=因為-1≤cosx≤1，所以當cosx=1，即x=2kπ，k∈Z時，ymin=應選B。

二、利用歸一法求三角函數的最值

若函數表達式中同時含有正弦函數和余弦函數，一般需要通過三角恒等變換將所給的函數式化為只含有一個函數名的形式。

例2求函數y=cos2x+5sinx-sin2x的最值。

解：函數y=1-sin2x+5sinx-sin2x=因為-1≤sinx≤1，所以當sinx=-1，即x=2kπ-k∈Z時，當sinx=1，即x=時

本題是利用三角函數的基本關系把函數的表達式轉化為一個角的同名三角函數的形式進行求解的。

跟蹤練習2：求函數y=sin2x+2cosx的最值。

提示：函數y=sin2x+2cosx=1-cos2x+2cosx=-（cosx-1）2+2。因為-1≤cosx≤1，所以當cosx=1，即x=2kπ，k∈Z時，ymax=2；當cosx=-1，即x=時，ymin=-4+2=-2。

三、利用有界性求三角函數的最值

在三角函數中，正弦函數和余弦函數具有一個最基本也是最重要的特征——有界性，利用正弦函數和余弦函數的有界性是求解三角函數最值的最基本的方法。

例3求函數的最值。

解：原函數變形為因為|sinx|≤1，所以所以-1≤y≤故函數y的最大值為最小值為-1。

跟蹤練習3：求函數的值域。

提示：原函數變形為因為|cosx|≤1，所以所以y≥3或故函數y的值域為

四、利用單調性求三角函數的最值

如果一個三角函數通過換元后的函數在它的定義域上具有單調性，則可利用函數的單調性求最值。

例4已知x∈（0，π），求函數y=的最小值。

解：設sinx=t，因為x∈（0，π），所以0＜t≤1。所以在（0，1）上是減函數，所以當t=1時，函數y有最小值為3。

跟蹤練習4：求函數 y=的值域。

提示：函數設sinx+2=t，因為sinx∈[-1，1]，所以1≤t≤3，所以y=t-在[1，3]上單調遞增[圖像類似對數函數，當x→0時，y→-∞，當x→+∞時，以y=x為漸 近線，且過點 （1，0）]。當t=1，即sinx=-1時，ymin=0；當t=3，即sinx=1時故函數y的值域為

五、利用數形結合法求三角函數的最值

由于sin2x+cos2x=1，所以從圖形考慮，點（cosx，sinx）在單位圓上，這樣對既含有正弦函數又含有余弦函數的三角函數的最值問題，可考慮用數形結合法求解。

例5求函數的最小值。

解：將函數表達式改寫成y 可看成連接點A（2，0）與點（cosx，sinx）的直線的斜率。由于點（cosx，sinx）的軌跡是單位圓的上半圓，所以求y的最小值就是在這個半圓上求一點，使得相應的直線斜率最小。設過點A的切線與半圓相切于點B，則kAB≤y＜0，可求得所以函數y的最小值為

跟蹤練習5：求函數的最大值。

提示：由函數設點P 為（sinx，cosx），點Q 為（-2，0），則可看成是單位圓上的動點P與點Q連線的斜率，如圖1所示。設過點Q的切線與圓相切于點P1時，直線的斜率最大。可求得所以可得y=1。所以函數y的最大值為1

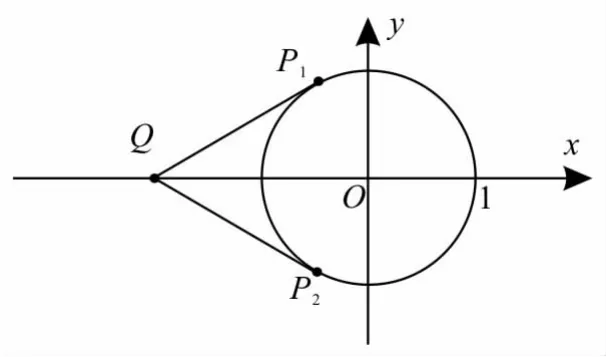
圖1

六、利用分類討論法求三角函數的最值

對于含參數的三角函數的最值問題的解答，往往需要對參數進行分類討論。

例6 設函數f（x）=cos2x+asinx-用a表示f（x）的最大值 M（a）。

解：函數f（x）=-sin2x+asinx-令sinx=t，則0≤t≤1，故g（t）=

本題主要利用換元法將原函數轉化為關于sinx的二次函數，根據sinx的取值范圍[-1，1]，利用對稱軸進行分類討論求出最大值。

跟蹤練習6：求關于x的函數y=-sin2x-2asinx+1-a的最大值。

提示：函數y=-sin2x-2asinx+1-a=-（sinx+a）2+a2-a+1。令sinx=t，則|t|≤1，故y=-（t+a）2+a2-a+1。

（1）若-1≤-a≤1，即-1≤a≤1，則t=-a時，函數y有最大值為ymax=a2-a+1（如圖2所示）。

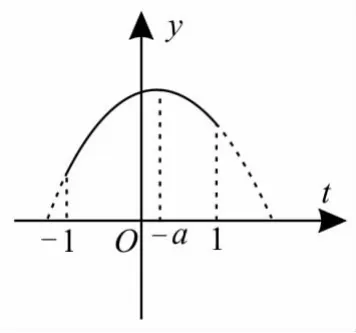
圖2

（2）若-a＜-1，即a＞1，則t=-1時，函數y有最大值為ymax=a（如圖3所示）。

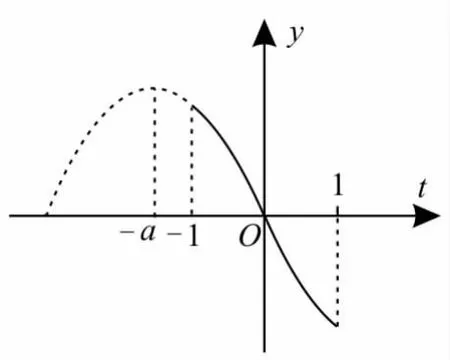
圖3

（3）若-a＞1，即a＜-1，則t=1時，函數y有最大值為ymax=-3a（如圖4所示）。

圖4