三角函數的圖像與性質的幾個重要問題
2019-05-28 11:47:24宋丹丹
中學生數理化·高一版 2019年4期
■宋丹丹
三角函數的圖像與性質是高考考查的重點,解決這類問題的關鍵是數形結合思想的應用。
一、求三角函數的解析式
例1函數y=Asin(ωx+φ)(A>0,ω>0,0<φ<π)在一個周期內的圖像如圖1所示,此函數的解析式為_________。
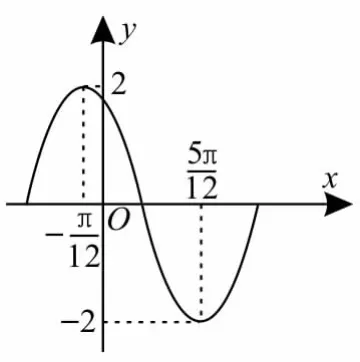
圖1
解:由圖像知可得ω=2。易知A=2,這時y=2sin(2x+φ)。將點代入可得所以即Z。故
二、求三角函數的單調區間
例2已知是函數f(x)=sin(2x+φ)的一個最大值點的橫坐標,則f(x)的一個單調遞減區間是( )。
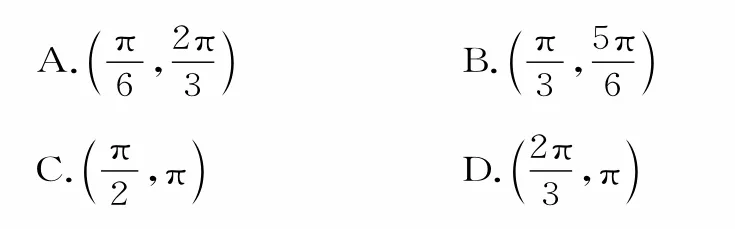
解:由是函數f(x)=sin(2x+φ)的一個最大值點的橫坐標,可得1,所以即φ=不妨取此時f(x)=令可得當k=0時,此函數的一個單調遞減區間為應選B。
三、求三角函數的周期
例3已知函數求函數f(x)的最小正周期和圖像的對稱軸方程。
解:由三角恒等變換可得函數f(x)=所以此函數的周期
四、三角函數的圖像變換
例4若將函數y=2sin2x的圖像向左平移個單位長度,則平移后圖像的對稱軸方程為( )。

解:將函數y=2sin2x的圖像向左平移個單位可得

