建模教學要突出“建”的過程
——以浙教版八上“3.3一元一次不等式（3）”為例

☉浙江省寧波市四眼碶中學 潘小梅

《義務教育數學課程標準（2011年版）》指出，模型思想的建立是學生體會和理解數學與外部世界聯系的基本途徑.模型思想是數學的基本思想，建模的過程是形成模型思想的主要途徑.那么，如何在日常教學中一以貫之地培育學生的建模能力，發展學生的建模思想呢？我在方程、不等式、函數等代數模型中進行了有意的嘗試，現以浙教版八年級上冊“3.3一元一次不等式（3）”，即一元一次不等式應用題教學為例，和各位同行交流、研討.

一、備課中的相關思考

浙教版八年級上冊第三章一共4節，第1節介紹不等式的概念，第2節介紹不等式的基本性質，第3節共分為3課時，前面2課時介紹不等式的解法，第3課時是一元一次不等式的應用，第4節是不等式組的概念及其解法.因此，在學習一元一次不等式的應用之前，學生已經掌握了不等式的概念及其解法，本課時的主要任務是建立一元一次不等式解決問題.從教材來看，本課時主要有兩塊內容，分別是以電梯運貨為背景提出兩道思考題和一道例題及其解答.如果僅從做題的視角來看，本節課15分鐘就可以完成.但是，怎樣讓學生在解決這些問題的過程中形成模型思想，遷移解決別的問題，這是我們進行建模教學的根本.正是基于這樣的思考，我在備課中思考了以下幾個問題：

問題1：什么是數學模型？

“數學模型”是一個含義很廣的概念，一切數學概念、數學理論體系、數學公式、數學方程及由此構成的算法系統都可以稱為數學模型.數學建模是一種數學的思考方法，是運用數學的語言和方法，通過抽象、簡化能近似解決實際問題的一種強有力的數學手段.本課需要建立的是一元一次不等式模型，即用不等式詮釋生活中的不等關系.

問題2：關于建模，學生的學習基礎是什么？

在本節課之前，學生已經接觸過大量的數學模型，如在加法運算中接觸了生活中的加法等各種運算模型，與一元一次不等式模型聯系緊密的是一元一次方程模型.在一元一次方程模型中，課本用天平形象地表明了同一種屬性的兩個量之間的等量關系.我認為，可以類比天平用蹺蹺板形象地表示不等關系，在同一種屬性的兩個量之間建立不等關系.

問題3：建模教學一般有怎樣的過程？

建模教學應該是一個潤物細無聲的過程，是一個自然發生慢慢浸透的過程.所以，我們杜絕采用告知、灌輸等方式，而是通過數學活動，讓學生在參與活動的過程中經歷、感悟、體會，在過程中形成模型思想.因此，本課的電梯運貨情境可以從原來的平面文字轉化為立體化情景呈現，以有利于學生感悟建模的必要性.

問題4：本課的教學目標是什么？

通過本課的教學，要掌握運用一元一次不等式建立模型的方法，還要讓學生在經歷建模的過程中感悟模型思想，體會抽象、轉化與化歸等思想方法.本課教學的重點是建立一元一次不等式解決問題，難點是怎樣讓學生在建模的過程中形成模型思想.

二、教學過程

1.情景展現，感受建模的必要性

師：同學們，在生活中，我們曾經碰到這樣的情景：（屏幕出示問題）如圖1，兩名賓館服務員要用電梯把一批貨物從底層搬到頂層，他們把一部分貨物搬上電梯時，發現電梯指示燈顯示綠色.于是，他們繼續搬入一箱箱貨物（動畫演示貨物搬運），現在的問題是，怎樣知道電梯能運幾箱貨物呢？

生1：直到電梯指示燈從綠色變為紅色，然后數一數一共有幾箱.

圖1

師：直到電梯指示燈顯示紅色，很多人都是這么想的！但是貨物有一堆，用這種方法很容易數錯.作為學過數學的你們，想想看，還有沒有其他的方法可以確定電梯能運幾箱貨物呢？

生2：老師，要知道電梯的額定限載量和一箱貨物的質量.

師：好！假設電梯的額定限載量為1000千克，每箱貨物的質量為50千克.

生3：因為要卸貨，還要考慮跟著貨物上電梯的兩個人的質量.

師：想得周到！假設兩個人的質量分別為60千克、80千克.現在能估算運送幾箱嗎？

生4：因為人和貨物的總質量不能超過電梯的額定限載量，所以得到50x+60+80＜1000.

師：非常好！我們解得x＜17.2，這說明最多能運送17箱.看來，運用數學工具可以快捷、精確地解決問題！

設計意圖：本教學片段把課本中用文字表述的電梯運貨問題以情境的方式再現過程，把課本中告知學生的數據“電梯額定限載量、貨物質量、賓館服務生的質量”讓學生以問題解決需要的方式呈現，凸顯問題解決的意識，讓學生感受建立不等式模型的必要性.

2.抽象提煉，形成雛形

師：現在如果將電梯的額定限載量用w千克表示，貨物的質量用p千克表示，賓館服務生的質量用m、n千克表示，要運送x箱，那么，x、m、n、p、w這些量之間應該具有什么關系？（用字母是為了保證學生不用算術計算，滲透模型思想）

生5：w＞px+m+n.

師：之前我們從天平聯想到方程，現在看到這個不等式，我想到了蹺蹺板：如圖2，你覺得蹺蹺板下壓的一端表示什么？上翹的一端又表示什么？

生6：下壓的一端表示電梯的限重，上翹的一端表示實際質量.

師：在這里，我們比較了兩個量就得到一個不等關系，只要知道其中的一些數據就可以很方便地進行計算.

設計意圖：本教學片段把具體的數字一般化，用字母表示，體現模型思想.接著由天平聯想到蹺蹺板，并把蹺蹺板作為不等關系的現實模型，形象地展示了不等關系，提煉了不等關系的雛形.

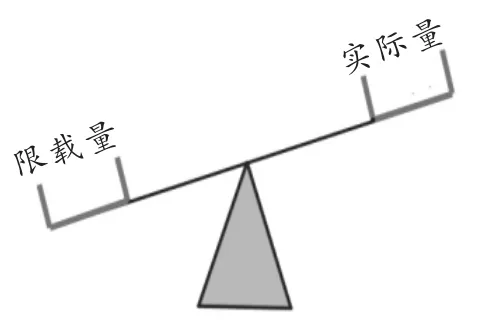
圖2

3.自主嘗試，初步感悟

師：現在有這樣一個問題，請你們自主嘗試解決：（屏幕顯示圖3）

2位老師帶了40個學生去參觀植物園

圖3

生7：（算術方法）50×16=800（元），42×20=840（元）.

師：看來想當然的事情并非想當然！懂點數學還能幫我們省錢！那么，人數至少是多少時，這樣買合算呢？

生8：設學生人數為x時，買50張合算，即16×50＜20（x+2），解得x＞38.

師：這里，不等號的左邊、右邊分別表示什么？

生9：左邊是買50張所付的款，右邊是按實際人數付的款.

師：同樣都是買票錢款，所以可以比較大小！請同學們想一想，在什么情況下，我們會想到用不等式模型解決？你能畫出蹺蹺板的左、右端分別表示什么嗎？

生10：比較兩個數量之間的大小關系時會想到用不等式模型解決.如圖4，蹺蹺板上翹的一端是買50張所付的優惠款，另一端是按實際人數付的款.

師：運用不等式建立關系可以解決許多問題，讓我們繼續看看哪些問題也可以用不等式解決.

設計意圖：有了前面電梯運貨問題的體驗，本教學片段以風景區買票問題為背景引發互相沖突的對話，讓學生進一步感悟用不等式建立模型解決問題的必要性，初步感悟不等關系是對同一個量的大小關系進行比較.

4.練習體悟，理解模型

師：現在，請大家一起看以下問題：（要求學生畫出不等式模型，不需求解）

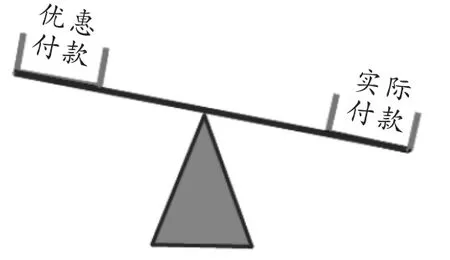
圖4

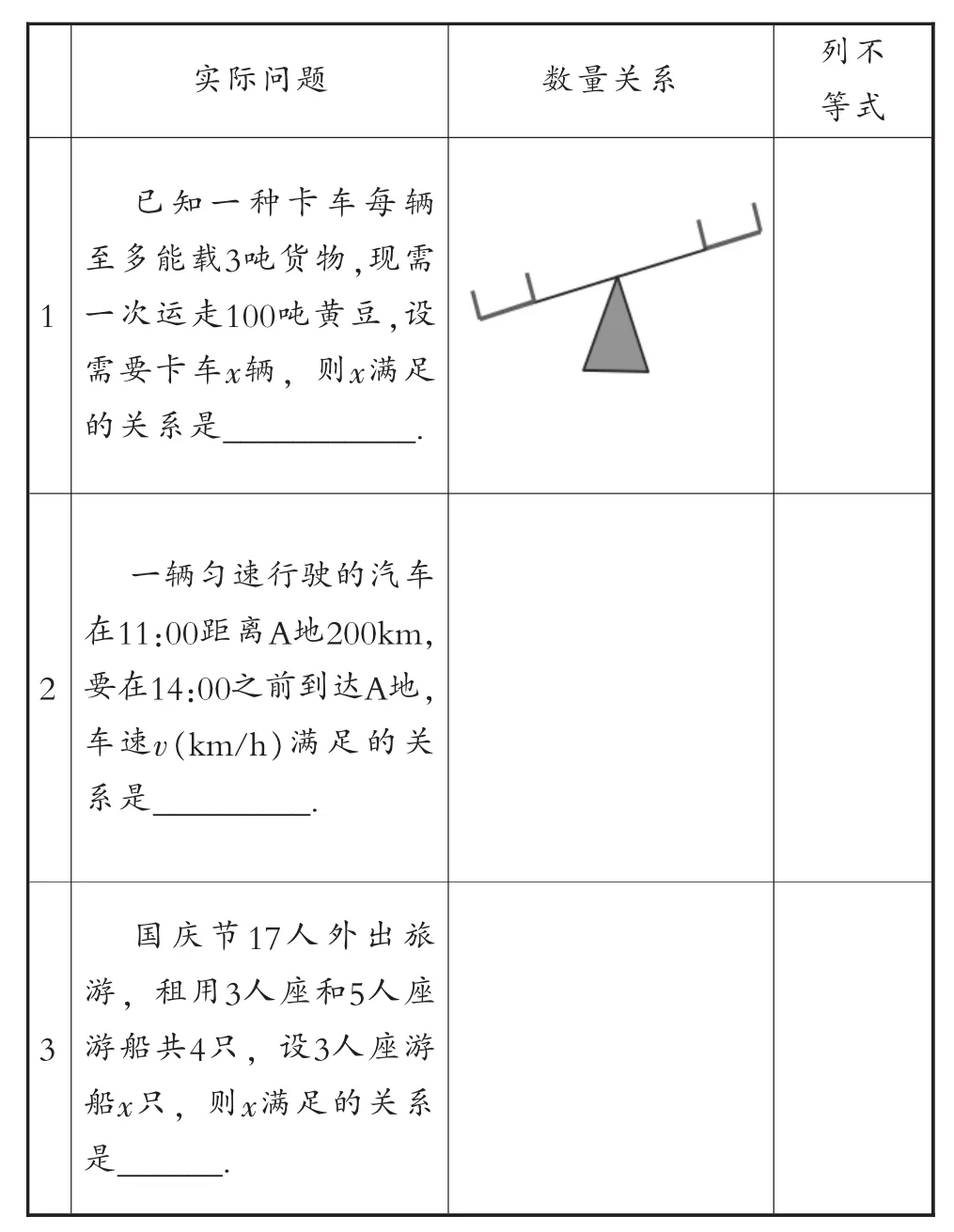
實際問題 數量關系 列不等式1已知一種卡車每輛至多能載3噸貨物，現需一次運走100噸黃豆，設需要卡車x輛，則x滿足的關系是___________.2一輛勻速行駛的汽車在11：00距離A地200km，要在14：00之前到達A地，車速v（km/h）滿足的關系是_________.3國慶節17人外出旅游，租用3人座和5人座游船共4只，設3人座游船x只，則x滿足的關系是______.

生11：如圖5，數量關系是能夠運載的質量大于實際運載的質量，得到不等式3x≥100.

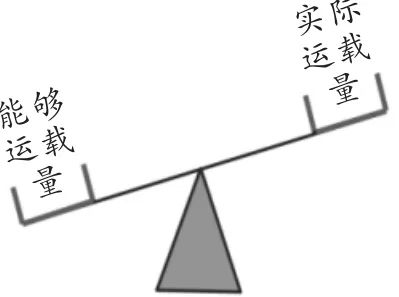
圖5

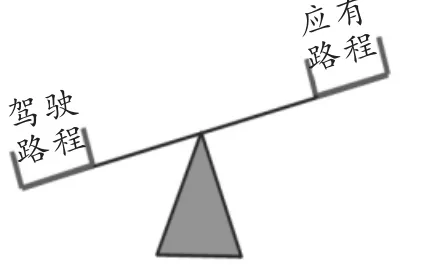
圖6

生12：如圖6，數量關系是駕駛路程大于應有路程，得到不等式3v≥200.

師：關于這個不等關系，還有其他不同列法嗎？

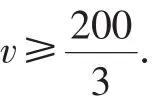
圖7

圖8

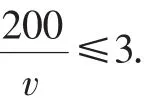
師：對同一個意義的量進行比較可以得到不同的不等式.第3題怎樣寫？

生15：如圖9，對能載客的人數和實際人數作比較，可以得到不等式3x+5（4-x）≥17.

師：從圖5到圖9這些蹺蹺板模型中，你發現怎樣的兩個量可以比較大小？

生16：同意義的、同單位的兩個量可以互相比較.

師：很好！對于同一種意義的兩個量，根據題意要求可以建立不等關系，要特別注意把比較的兩個量化為同單位的兩個量.

設計意圖：本教學片段用三個練習詮釋不等關系的建立方法，3個練習各采用不同的量，練習1是質量的比較，練習2是距離、速度、時間的比較，練習3是人數的比較，量綱不同，但同一個量都可以進行比較.只要求學生利用蹺蹺板列出不等式，不需解不等式，是為了強化對不等式數量關系的理解.

5.共研例題，運用模型

師：請大家閱讀課本例題，先嘗試自己獨立思考解決，也可以一起合作討論.

例有一家庭工廠投資2萬元購進一臺機器，生產某種商品.這種商品每個的成本是3元，出售價是5元，應付的稅款和其他費用是銷售收入的10%.問：至少需要生產、銷售多少個這種商品，才能使所獲利潤（毛利潤減去稅款和其他費用）超過投資購買機器的費用？

生17：本題的數量關系是：利潤超過投資購買機器的費用，其中利潤是毛利潤減去稅款和其他費用，因此可以建立不等關系.

師：如何設未知數呢？

生18：設至少需要生產、銷售x個這種商品，才能使所獲利潤超過投資購買機器的費用.

師：其他同學有意見嗎？

生19：我覺得應該去掉“至少”兩個字，因為這是某個確定的值.

師：講得好！請大家參看書本解題過程：

解：設生產、銷售這種商品x個，則所得利潤為（5-3-5×10%）x元.

由題意得（5-3-5×10%）x＞20000.

解得x＞13333.3…

答：至少要生產、銷售這種商品13334個.

師：同學們，回顧一下：列不等式解實際問題具有怎樣的過程？

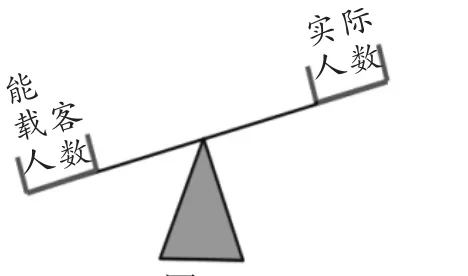
圖9

師生共同歸納如下（如圖10）：

練習：某業主貸款2.2萬元購進一臺機器，生產某種產品.已知產品的成本是每個5元，售價是每個8元，應付的稅款和其他費用是售價的10%.若每個月能生產、銷售2000個產品，問：至少幾個月后能賺回這臺機器的貸款？

設計意圖：本教學片段的例題和練習讓學生自主閱讀和思考，運用前面獲得的經驗解決問題.這里教師對學生容易發生錯誤的設未知數問題進行了提醒.

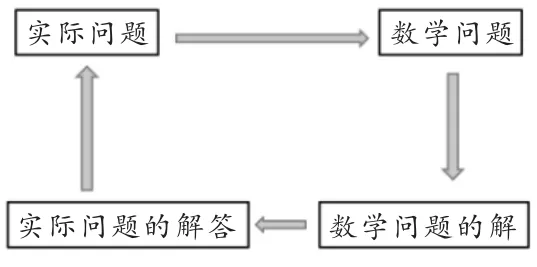
圖9

6.總結提煉，內化思想

師生共同小結：在生活中，當我們要比較或確定兩個量之間的大小關系時，常常會選擇不等式模型（出現蹺蹺板），建立不等式解決問題.在這里我還想到了許多不等關系在一定條件下能夠互相轉化.比如滴水能夠穿石，一滴柔軟的水的力量遠遠小于堅硬的石頭的力量，但是長此以往，卻能穿透堅硬的石頭.還聽說過“千里之堤，潰于蟻穴”，告訴我們小錯誤可能造成大損失！所以，正像荀子說的，“不積跬步，無以至千里；不積小流，無以成江海”“鍥而不舍，金石可鏤”送給四眼碶中學1911班的你們，愿你們堅持努力，成為“金石”！

設計意圖：梳理建立模型的方法是對同一個量進行大小比較.從不等關系聯想到生活中不等量之間的轉化，將這種不等關系折射的哲理滲透進學生的思想中，讓學生的情感得到升華.

圖10

三、關于建模教學的思考

1.合適的問題（或問題情境）是學生經歷建模過程的保障

數學模型是高度概括的產物，從現實生活或具體情境中抽象出數學問題，用數學符號建立方程、不等式、函數等表示數學問題中的數量關系和變化規律，求出結果并討論結果的意義，這些內容的學習有助于學生初步形成模型思想.在這里，現實生活或具體情境就是模型提煉的載體，合適的載體有利于學生在問題解決的過程中形成數學模型.如本課教學中，需要學生提煉的數學模型是不等式，在現實生活中表現為兩個具有同樣意義的量之間的大小比較.電梯運貨和購買門票這兩個問題既是學生身邊常見的現實問題，又能由學生的生活經驗得到電梯運載量少于電梯限載量，購買門票費用便宜指的是花費總額少，是表示不等關系的合適問題.在創設問題和問題情境時，我們可以根據模型賦予學生熟悉的現實意義，避免生澀難懂，脫離學生現實.

2.設計有效的數學活動，讓學生經歷完整的建模過程

問題（或問題情境）是學生參與建模活動的載體，要讓學生經歷建模的過程，需要教師組織有效的數學活動，讓學生經歷建模的過程.筆者認為，建模的一般過程是：提煉模型→識別模型→理解模型→運用模型.提煉模型就是把實際問題數學化并獲得解決，識別模型的過程就是讓學生在適當的變式情境中感悟模型特征，理解模型的過程就是充分理解模型的由來方法，運用模型可以理解為數學模型回歸現實生活.如本課教學中，通過電梯運貨感悟模型的必要性并提煉出形象表示不等關系的蹺蹺板模型，通過購買門票讓學生識別模型，進一步感悟不等關系的特征，接著通過三道練習讓學生理解列不等式解決問題就是對同意義的量進行大小比較，最后的例題和練習就是模型運用的過程.在建模的過程中，教師要搭建學生參與數學活動的時間和空間，通過獨立思考、合作交流、動手探究經歷建模的過程.

3.歸納反思和及時感悟是形成模型思想的重要途徑

模型反映了五彩世界萬千事物蘊含的共性特點，提煉這些共性特點并在學生的頭腦中固化下來，需要一個漫長的過程，需要教師在日常的教學中一以貫之地進行滲透和適時進行反思和感悟.本課教學中，教師多次創造學生反思和感悟的時機，當學生由電梯運貨問題列出不等式時，教師引導學生把具體的數一般化并提出蹺蹺板模型；在購買門票問題后，教師追問“在什么情況下想到列不等式”，在練習后教師又追問“怎樣的兩個量可以進行大小比較”，讓學生反思得到不等式表示的是不等關系，所有的不等式都是對同一種意義的兩個量進行大小比較；在例題后引導學生歸納得到解決實際問題的一般過程，在課尾由不等關系聯想到生活中的哲理.這些反思和感悟的過程滲透在建立模型的過程中，讓學生通過不斷體悟獲得模型思想，內化為自身的一種核心素養.