數形結合悟大小，經驗連用得新知*
——“有多大”的教學感悟

☉福建省廈門市五顯中學 林振德

《義務教育數學課程標準（2011年版）》（下稱《課標（2011版）》對學生的估算能力提出了一定的要求.在人教版初中數學教材中，安排了不少近似取值計算的問題，這些問題的解決能較好地發展學生的估算能力.在“6.1平方根”一課中，更是安排了探索“有多大”的活動，直接指向了估算能力的培養，對學生數感的發展十分有利.然而，由于教材給出的是純數字大小比較，對于沒有相關經驗的學生來說，想要得出被哪兩個數夾在中間是十分困難的.為了幫助學生突破認知難點，筆者從教材給定的拼圖實驗出發，在經驗的連用中實現數形結合，幫助學生較好地感知了的無理數“特質”.現呈現教學歷程及個人的感悟，供大家參考.

1.拼圖探究

學生活動1：用兩個面積為1dm2的正方形拼成一個面積為2dm2的大正方形.

教師將邊長為1dm的兩個正方形貼在黑板上，并將面積與邊長板書.學生給出“將兩個正方形沿著對角線剪開，然后將四個直角三角形拼在一起，就是面積為2dm2的正方形”的方法，并利用教師給出的正方形形成圖1中的拼圖貼在黑板上.

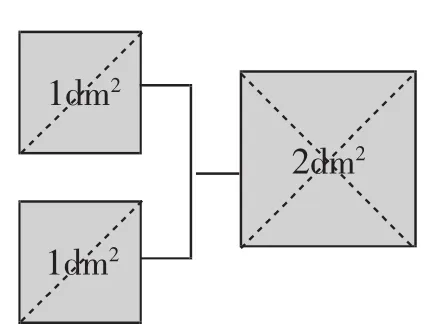
圖1

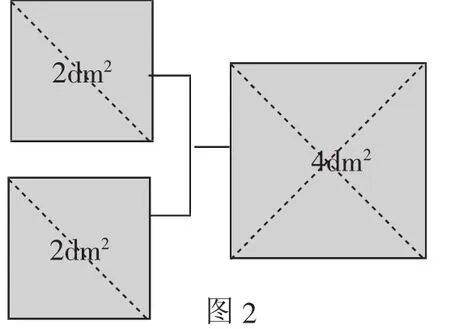
圖2

學生活動2：用面積為2dm2的兩個正方形拼成一個面積為4dm2的大正方形.

根據活動1的經驗，學生很快給出圖2中的結果，教師順勢將正方形的邊長和面積進行了板書，最終形成圖3所示板書.

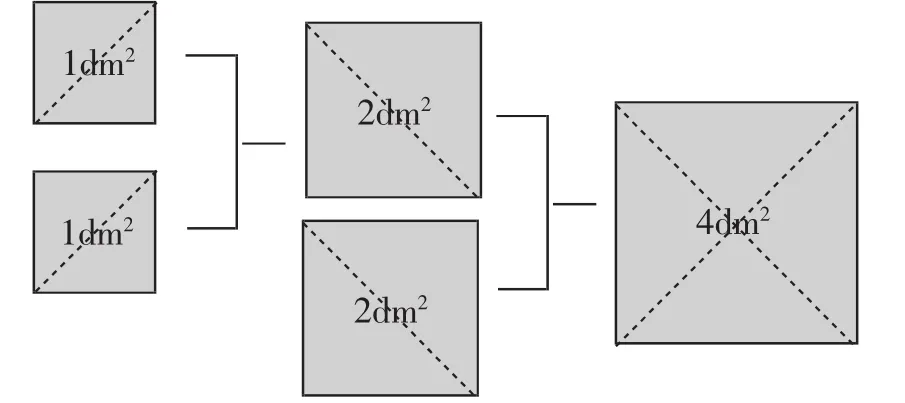
圖3

2.估算大小

通過剛才的拼圖，我發現正方形的面積越大，其邊長就越長；反之，正方形的邊長越長，其面積也就越大.邊長為1dm的正方形面積為1dm2；邊長為dm的正方形面積為2dm2；邊長為2dm的正方形面積為4dm2.圖3中，三個正方形的面積由小到大排序為1＜2＜4，所以，其邊長也應是1＜＜2.

教師肯定了學生的發現，并指出正方形的邊長與它的面積有很大關系.進而讓學生找出一個與更接近的數.學生猜想：1.2、1.3、1.4、1.5……

教師進一步追問，邊長為1.4幾的正方形的面積與2更接近呢？學生分組探究，分別用計算器計算1.41、1.42、1.43、…、1.49等9個數的平方，找尋出平方最接近2的數.3分鐘后，不少小組給出結論：1.41＜＜1.42……

3.總結方法

二、教學過程簡析

“估算大小”環節，教師引導學生反復經歷由形的大小關系抽象出數的大小關系，再由數的大小關系感知形的大小.基于這樣的經驗連用，學生先后得到了1.4＜＜1.5、1.41＜＜1.42、1.414＜＜1.415等三個小數位數遞增的越來越逼近的取值范圍.這不僅讓學生對的“無理”特性有了較深刻的認知，同時將數形關聯的經驗進一步鞏固，使學生真正體會到數形結合的價值.

三、教后思考

1.注重數形結合，彰顯關聯價值

數形結合是一個非常重要的數學思想，在解決很多數學問題的過程中都會發揮重要的作用.而數與形的關聯分析是其價值真正得以展現的基本形式.所以，在數學教學中，我們要重視數與形的關聯，要注意讓學生經歷數向形轉化或形向數轉化的過程，因為只有有了這樣的過程體驗，學生才可能真正體會到數形結合思想的內在價值.在本文所述的片段中，學生首先從形的角度感知并抽象出數的大小關系式，再從數的角度體會到形的大小關系，這種基于形數對照下的大小關系對照比較對學生真正感知到數形關聯的價值是非常有好處的.因此，教師在教學過程中始終以學生為主體，讓他們自主拼圖、合理猜想并計算驗證，將數與形的內在聯系很好地融入到學生自主探索的歷程之中，再通過師生間的互動交流將這些內在聯系逐步明晰，從而使整個探究活動緊扣教學目標尤其是本節課的能力目標奮力前行，取得較好的教學效果也在情理之中了.

2.立足活動經驗，強化遞進應用

數學知識的生成與應用一般都在數學活動之中.而在數學活動中，除了可以形成顯性的數學基礎知識與基本技能，還可能會有數學基本活動經驗伴隨著生成.這些活動經驗是學生進一步開展數學活動的基礎.因而，我們在探索新的數學知識時，要特別注重學生既得經驗的再應用，讓學生在熟悉的路徑上探索并獲得新的知識.正如第斯多惠所言“：教學的藝術不在于傳授知識，而在于激勵、喚醒、鼓舞.”數學教學的藝術也應是在喚醒舊的知識與經驗的同時生成新的知識與經驗.以本文所述片段為例，對于拼圖尤其是拼正方形，學生在小學中就已經積累下較為豐富的操作經驗，教學起始教師讓學生進行拼圖操作，這就是喚醒.在拼圖過程中，學生的形變但面積不變、疊合等邊、直角拼平角、（正方形）“形大邊長”等方面的經驗被逐一喚醒，而在接下來的教學中，教師并沒有停留在這些經驗知識中，而是將（正方形）“形大邊長”這一經驗強化應用，讓學生對“有多大”的認知隨著小數位數的遞增不斷加深，實現獲取新知與固化經驗的學習目標.

3.用好信息技術，優化探索歷程

數學課，無論是新授課還是復習課，都應有課時教學重點.每節課的教學重點指向各不相同，有的指向數學的基礎知識，有的指向數學的基本技能……雖然課時教學重點各有不同，但所有的教學內容和教學流程都應努力服務于教學重點的突破.因而，數學教學不應為課時邊緣探索耗費太多的教學時間，可用現代信息手段替代邊緣（與課時重點關聯不大的）操作.比如，本節課上多個數的平方的計算，從1到1.4，再到1.41，再到1.414，這期間要算不下二十個數，如果不利用計算器，而是直接筆算，耗費的時間一定會很多，這無形中會讓探索的重心偏移到平方運算結果的對錯上去，而不再是介于哪兩個數之間了.如此教學，顯然無法突出本節課的教學重點，對課時目標的達成是十分不利的.在本節課上，除了簡單的1、2這兩個數的平方，其余各數的平方運算均利用計算器進行，極大地縮短了運算時間，為學生將時間用到數的大小比較上提供了可能，突出了教學重點，取得了較好的效果.F