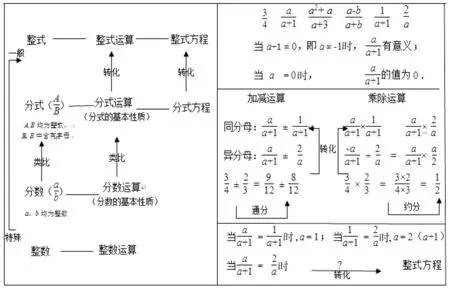
重組·搭架·定向：數學單元教學的旨歸
——以“分式單元教學（第1課時）”為例

☉江蘇省如皋市東陳鎮雪岸初級中學 陶成龍

2018年暑假，我有幸成為由江蘇省著名特級教師李庾南老師領銜的南通市鄉村初中數學骨干教師培育站的學員，開始零距離向李老師學習“自學·議論·引導”教學法.近期，筆者有機會參加了由南通市教育科學研究院組織的南通市初中數學青年教師優課評比活動.本次比賽采用事先預告課題的辦法，上課的內容是人民教育出版社義務教育教科書《數學》八年級上冊（2013年版）第十五章“分式”第1課時（全章單元教學）.通知中明確指出本課屬于建構型的單元教學課型，不是教材內容的第1課時.剛剛接到比賽課題時，我感到茫然，不知何謂單元教學.在接下來研修的過程中，我重點閱讀了李庾南老師的著述《自學·議論·引導教學論》，以及上網查閱相關資料，方才略有眉目.原來單元教學指的是根據數學知識發生的規律、內在的聯系及學生的學習情況，將學材分為單元或知識模塊，著重幫助學生建構知識系統，從整體上把握教學要求，再著眼于分課時學習系統中的知識［1］.

基于上述認識，我將本節課的教學設計定性為“重組教材謀全章，著眼整體搭框架，預留懸念定方向”.本文就以這一課的教學設計為例，通過對設計意圖的闡述，談談對單元教學的一些粗淺的認識和做法，敬請同行批評指正.

一、教學設計

1.教學目標

（1）了解分式的概念及產生的根源.

（2）搭建全章整體框架，感悟數式相通.

（3）經歷與分數類似的學習過程，體會類比、轉化和由特殊到一般是研究數學的基本思想方法.

2.教學過程

活動1：數式相通之追溯概念本源.

問題1：對任意兩個整數進行加、減、乘、除中的任意一種運算，所得的結果仍然是整數嗎？請舉例說明.

問題2：對任意兩個整式進行加、減、乘、除中的任意一種運算，所得的結果仍然是整式嗎？

請完成以下計算：a+（a+1）=______；a-（a+1）=______；a（a+1）=______；a÷（a+1）=______.

設計意圖：單元教學首先要解決為什么要學的問題.數學知識的產生與發展無非來源于兩方面，一是實際生產和生活的需要，這也是它的應用價值之所在；二是基于數學內部發展的矛盾與沖突，這種暫時的矛盾與沖突都會促進人類認識事物觀念和思維方式的轉變，重新完善原有對象或者建構新的對象以求實現數學內部的自我調和，從而推動數學進一步的發展.作為分式單元教學起始課的分式概念的引入，教材采用的是從學生熟悉的實際生活導入，讓學生運用分式表示數量關系，從而讓學生體會分式也是刻畫現實世界數量關系的一種工具.筆者通過設置數學內部問題情境即類比整數間除法運算是不封閉的，從而產生了分數，繼而發現整式間的除法運算也是不封閉的，從而產生了分式這一新的概念，這種遵循代數式體系發展的客觀規律和需要凸顯出濃濃的數學味，同時為活動2探究分式間的四則運算起到鋪墊作用.

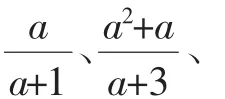
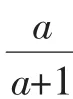
追問意圖：通過讓學生觀察分數和分式之間的異同點，類比分數的形式自主歸納出分式的定義并且通過后面兩個分式使學生深刻領悟到判別一個式子是否為分式的關鍵是看分母中是否含有字母，與分子是否含有字母無關，同時通過舉例讓學生感受分數和分式之間是一種特殊與一般的關系，為后面學生感悟到分式運算的本質其實仍然是分數間運算起到了鋪墊作用.最后順勢引導出分式有意義的條件和分式的值為0的條件.

活動2：數式相通之搭建全章整體框架.

問題3：請同學們從以下三個分式中任取兩個，列出關于你所選的兩個分式間的加、減、乘、除的四種運算題，并探究計算的方法（不需要算出結果）.

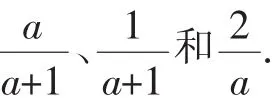
設計意圖：本活動設計目的主要是讓學生通過類比分數間的四則運算方法探究分式間的四則運算，使學生認識到分式間的運算同樣要經歷通分和約分這兩個過程，而這一過程的實施必須以分式自身的性質作為依據，這就產生了類比分數的基本性質研究分式的基本性質的需要.同時讓學生感受到分式間的運算其實歸根結底仍然是整式間的運算問題.另外，向學生滲透研究代數式的套路與方法，即當我們面臨一個新的代數式時，除了給出它的定義，還要研究它的性質，以及最關鍵的是研究它們間的運算方法，這是研究代數的重要內容，也為后期如何研究另外一類代數式（二次根式）做鋪墊.

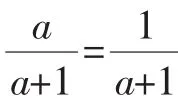
追問意圖：我們知道，這三個分式的值隨著字母a取值的變化而各自變化，但是當a取何值時，其中兩個分式的值有沒有可能相等呢？這也理應成為學生思考的一個問題，從而產生了認識分式方程及解分式方程的需要.這個追問除了可以提前向學生滲透函數思想，更為關鍵的是為完善分式這一章的知識框架結構做準備.

活動3：課堂小結.

（1）通過本節的課學習，還有哪些問題有待解決？你感興趣的還有哪些方面？

（2）請同學們對照老師的課堂板書思考：如果你是教材編寫者，該如何編寫本章內容？

設計意圖：通過這樣的課堂小結，一是讓學生關注分式間的四則運算的結果是否仍然是整式或分式的問題，呼應前面的封閉性問題，從而實現各活動間起承轉合，一脈相承；二是解決在實施單元教學時怎么去學習，以及在后續分單元實施時學習什么內容的問題，即讓學生明確后續研究的方向、內容和方法.

3.板書設計

二、幾點思考

作為全章單元教學的第1課時，教師不能像獨角戲的扮演者那樣向學生做直陳告白式的講演，而是要讓學生在“做”數學的過程中追溯數學知識產生的根源，明晰知識的發展脈絡［2］.本課教學結合學生的年齡特征和認知基礎，以運算的封閉性問題，即在數或式進行四則運算的過程中是否出現陌生的數或式作為主線，設置一連串的問題，創造性地將教材提供的素材進行了重新整合，這樣學生就會明白數學知識的源頭，領悟到數學的本質，感受到學習數學的價值，從而激起學生探究的欲望和興趣.只有讓學生從內心深處產生這樣一種強烈的求學愿望，學生才會真正主動地、獨立地、創造性地開啟本章內容的探尋之旅.

作為全章單元教學的第1課時，并不是要求教師在一節課中將知識點逐一深入展開，平均用力，更多的是一種學法的指導.俗話說，學會學習往往比學會知識更重要.這就要求教師在進行單元首課教學時，要恰如其分地把握教學的“度”，不能操之過急，也不能浮于表面，而是要著力于核心知識的生成與核心方法的感悟.本節課中，我并沒有要求學生計算出幾個分式運算的結果，也沒有讓學生去求出分式方程的解，重點放在了通過讓學生類比小學時學習分數的過程了解分式的概念及其產生的根源，幫助學生搭建全章整體框架，從而感悟到數和式的一致性，體會到類比、轉化和由特殊到一般是研究數學的基本思想方法.

作為全章單元教學的第1課時，并不是要求教師在這一節課中按照教材中章節順序從前往后一一羅列，鋪陳疊加，更多的是一種基于知識間邏輯關系的內容框架的建構.這就要求教者根據學生的認知基礎和數學知識之間前后邏輯聯系重組教材.本節課中，我遵循“以課標為準繩，以學情為依據，以教材為藍本”的原則，將原有的教學材料進行了重新整合，將數學內部的邏輯關系進行了重新融通，通過3個問題和3個追問串聯出全章的知識框架，幫助學生建立一種既見樹木又見森林的整體框架，使知識以“系統中的知識”出現在學生面前，這樣學生就會胸懷全局，從系統的高度對今后將要學習的內容展開具體的研究，學習的盲目性就會大大降低.久而久之，學生就能自主地探究新的數學問題，從而培養學生科學的學習方法和思維方法.