改編例、習題:讓“教教材”走向“用教材教”
——以人教版八下教材例、習題改編為例
☉江蘇省海安市海陵中學 吳 晶
鐘啟泉教授指出:“用教材教”與“教教材”是區分新、舊教學的分水嶺.所謂“教教材”,就是指那種照本宣科的講課本,講例、習題,而“教教材”則需要對教材內容進行深度理解.具體研讀教材的角度很多,我們見到的很多文獻中關于教材解讀側重于對數學知識引入、呈現或前后貫通的研究,針對教材上例、習題的改編研究則不是很多.本文結合具體的教材例、習題改編案例,闡釋我們的做法與思考.
一、教材例、習題改編案例
案例1:“海倫-秦九韶公式”習題改編.
教材以“閱讀理解”介紹了著名的“海倫-秦九韶公式”,并配一道習題:
在△ABC中,BC=4,AC=5,AB=6,請用海倫-秦九韶公式求△ABC的面積.
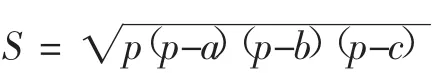
這個知識點非常重要,不但是數學文化的教育與熏陶,而且在各級考試中經常作為命題熱點,所以在期中考試、期末考試復習時仍然要進行訓練.但到了期中、期末考試時,不能像新授二次根式階段一樣教學,而應該與不同單元的數學知識進行綜合,比如,將該知識點與勾股定理綜合起來,可以改編如下:
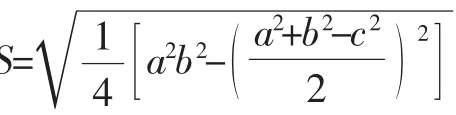
設計意圖:這道習題引導學生復習秦九韶公式,然后運算之后的講評環節可以引導學生再利用海倫公式算一次,比較不同公式的一致性.思維深刻的學生可能會發現這三邊長恰能圍成一個直角三角形,于是可以利用勾股定理逆定理判定直角三角形,再直接利用兩條直角邊的乘積的一半來快速解出該三角形的面積,訓練學生思維的靈活性.
案例2:共頂點雙等腰直角三角形問題.
教材上勾股定理習題中有如下一道共頂點的雙等腰直角三角形問題:
如圖1,△ACB和△ECD都是等腰直角三角形,CA=CB,CE=CD,△ACB的頂點A在△ECD的斜邊DE上.求證:AE2+AD2=2AC2.(提示:連接BD)
解法簡析:該題比較經典,在八年級上學期學習全等三角形時就在不少教輔資料上進行了比較泛濫的訓練,一方面說明教輔資料的超前訓練,另一方面說明這類問題更本質的是考查全等三角形的判定,當然,這類習題也是網絡上有些人總結的所謂“手拉手模型”.那么,該如何發揮這道習題的教學功能,追求做一題、會一類、通一片的教學效果呢?我們給出如下改編:
教材改編題2:如圖1,△ACB和△ECD都是等腰直角三角形,CA=CB,CE=CD,△ACB的頂點A在△ECD的斜邊DE上.
(1)連接BD,求∠BDC的度數.
(2)若AE=3,AD=4,求AB的長.
(3)求證AE2+AD2=2AC2.
(4)探究線段AE、AD、BC之間的數量關系,并說明理由.
(5)設CE=5cm,分析四邊形ACBD的面積是否變化.如果變化,指出它的面積最大值;如果不變,請說明理由.
改編意圖:通過上述5個系列問題,可以讓學生對這個基本圖形可能的一些設問都有所訓練,對圖形中線段與線段之間的關系、角與角之間的關系、不同三角形之間的關系等都有較全面的研究,實現做一題、會一類的教學效果.另外,從九年級圓的角度來看,該題中四邊形ACBD的四個頂點都在同一個圓上,將來可以站在更高的視角來理解這個問題的結構,在圓的教學過程中或中考復習階段,仍然值得把這個圖形進行改編開發成系列問題,發揮一題多練的教學功能.
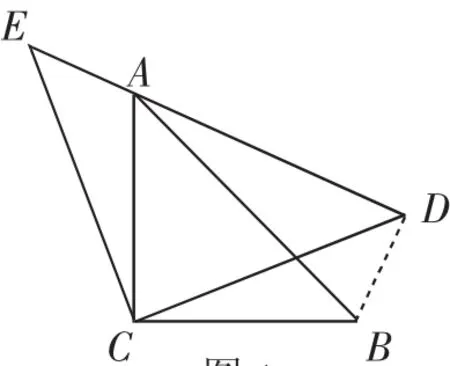
圖1
案例3:折疊黃金矩形.
教材在平行四邊形一章的數學活動中安排了折疊黃金矩形,限于篇幅,這里不鏈接該題(該題在不少地區期末考試、中考試題中都曾出現過).以下只是針對該教材活動給出系列設問,如下:
問題1:圖形中只有一個黃金矩形嗎?為什么?
問題2:在圖形中能否再折疊一次,得到一個60°的角?
改編意圖:這兩個問題可將探究成果擴大,并關聯教材上另一個數學活動“折紙做60°、30°、15°的角”,有利于學生將所學內容關聯起來,也是踐行鄭毓信教授提出的“數學知識不求多,而求聯;數學習題不求難,而求變”.
案例4:研究絕對值函數.
教材在一次函數一章的習題中初步給出了絕對值函數,如下:
(1)畫出函數y=|x-1|的圖像.
(2)設P(x,0)是x軸上一個動點,它與x軸上表示-3的點的距離為y,求y關于x的函數解析式,并畫出這個函數的圖像.
教學組織:這道題的兩小問之間看似條件互不關聯,但是第(1)問給第(2)問提供了解法指導,起到了預熱、鋪墊作用.教學時,要充分利用這種鋪墊式問題,在學生處理第(2)問遇到困難時引導學生退回到上一問,思考解題方向.在此之后,可給出如下變式問題:
設Q(0,t)是y軸上一個動點,它與點(0,-3)的距離為s.
①求t的函數s的解析式;
②直接寫出該函數圖像的最低點坐標:_______.
改編意圖:從x軸變式到y軸上一點,并利用絕對值函數的圖像分析最低點,對教材習題進行鞏固和拓展,讓學生初步感受絕對值函數的一些性質.
二、改編教材例、習題的幾點思考
1.明辨教材例、習題的教學價值與地位
旅美數學教育學者馬立平博士所指出的深刻理解數學知識經由鄭毓信教授推介之后,得到不少同行的積極響應,近些年在不少課例研究、命題研究的文獻中都能看出研究者們對深刻理解數學知識的追求.我們關于改編教材例、習題的做法也是基于深刻理解初中數學知識的基礎上進行的,比如,教材上例、習題很多,改編時如何取舍呢?需要站在初中階段數學知識的深刻理解的高度進行選取.比如,上文案例1中,我們選定了海倫公式作為改編,同時關聯了勾股定理的逆定理,這些內容(二次根式的化簡與運算、勾股定理)都是初中階段的核心知識,同時滲透了數學文化.案例4中絕對值函數雖然不是初中階段的核心知識,但是改編習題主要是讓學生對點到點的距離公式、函數概念、函數研究方法有深刻理解和靈活運用.
2.變式改編要源于教材又高于教材
選取教材例、習題進行變式改編,要源于教材又要高于教材.具體來說,有些考題明明與教材無甚關聯,卻被有些命題者貼上源于教材的標簽.而像上文中的幾個題例,都是教材中明確存在的習題或活動素材,這里針對它們的改編就不止于再練一次,重復訓練,而是在原題的基礎上變式拓展、成果擴大、走向一般.比如案例2,不僅有效訓練了共頂點的雙等腰直角三角形帶來的性質,同時將這個基本圖形可能的命題考查方向都帶領學生進行充分的探究,并且關聯著后續圓的知識.再比如案例3,教材只是研究折疊出一個黃金矩形,而我們再次引導學生發現圖形中還有另一個黃金矩形,這也是改編習題要“高于教材”的具體追求.
3.變式改編重在引領學生想深、學透
踐行教材例、習題變式與改編是研究教材的一種重要方式,而不是“另選”(更多的是快速從一些資源網站直接下載、復制而來)大量與教材無關的所謂中考試題、名校模考試題.其目的是引領學生想深、學透,實現教材資源教學價值的更大化的一種追求.“鄭毓信教授倡導的數學知識不求多而求聯,數學習題不求量而要求變”,以及通過例、習題教學,促進學生想深、想透,都是我們變式改編例、習題的努力目標.
三、寫在后面
教材研究是經典教研課題,我們選擇改編例、習題的研究方式才剛起步,還有待深入,文中提及的一些題例打磨還不夠充分,期待更多同行參與研討,加深我們對改編教材例、習題的認識.

