立足學生發展，讓學生真正“有話可說”
——記初三數學復習課“探索數式規律性問題”

☉浙江省湖州市第五中學鳳凰校區 白 艷

規律性問題是近年來中考數學的熱點題，這種題型可考查學生觀察、比較、探索問題的能力.學生必須具有綜合的數學能力和實踐能力，才能較好地解答此類問題.在實際教學過程中，學生面對這種題目往往手足無措，無法找到其內在關系.

針對學生的這一問題，筆者開設了一節專題復習課“探索數式規律性問題”，以期在方法上對學生進行一些指導和幫助，并在第一次上課—評課、修改教學設計—第二次上課（不同班級）—課后反思的過程中學到了很多.

一、備課、教學初體驗

初中三年的數學學習中，大多數學生對簡單的規律性問題的解決能做到得心應手，但遇到偏難的問題時，會束手無策，因此在初次備課時，筆者的側重點在于較難的規律性問題，具體的教學設計如下：

師：今天我們來研究專題：規律性問題，在中考題中主要有以下幾種類型.

【初試數式規律】

呈現例題：

觀察下列數的排列規律，并完成填空.

1.1，4，9，16，25，______，49，…，則第100個數是______.

2.0，3，8，15，24，…，則第2002個數是______.

學生回答，教師點評，并提問：在解題時，你認為解題的關鍵是什么？

解題錦囊：

編序號—找“關系”—驗證.

探囊取物：

1.古希臘數學家把數1、3、6、10、15、21、…叫作三角形數，其中1是第1個三角形數，3是第2個三角形數，6是第3個三角形數，…，以此類推，那么第9個三角形數是____，2016是第____個三角形數.

2.觀察下列等式：

……

按上述規律，回答以下問題：

（1）用含n的代數式表示第n個等式：an=______；

（2）a1+a2+a3+…+an=______.

3.下面是按一定規律排列的一列數：

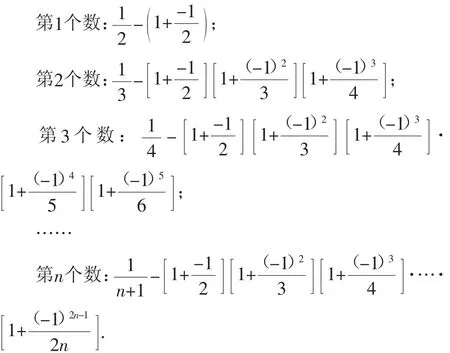
那么，在第10個數、第11個數、第12個數、第13個數中，最大的數是（ ）.

A.第10個數 B.第11個數 C.第12個數 D.第13個數

【再探圖形規律】

例題教學：如圖1，自左至右，第1個圖由1個正六邊形、6個正方形和6個等邊三角形組成；第2個圖由2個正六邊形、11個正方形和10個等邊三角形組成；第3個圖由3個正六邊形、16個正方形和14個等邊三角形組成……按照此規律，第n個圖中正方形和等邊三角形的個數之和為______.

圖1

解題錦囊：

編序號—找“關系”—驗證.

探囊取物：

如圖2，圖（1）是一個水平擺放的小正方體木塊，圖（2）、（3）是由這樣的小正方體木塊疊放而成的，按照這樣的規律繼續疊放下去，至第7個疊放的圖形中，小正方體木塊總數應是（ ）.

A.25 B.66 C.91 D.120

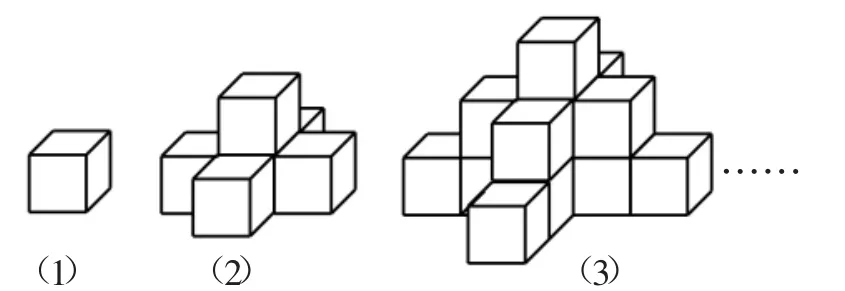
圖2

解題錦囊：

編序號—分類（累加、分區、循環）—找“關系”—驗證.

【三探坐標系中的規律】

探囊取物：

1.如圖3，在平面直角坐標系中，直線l：y=x+2交x軸于點A，交y軸于點A1，點A2、A3、…在直線l上，點B1、B2、B3、…在x軸的正半軸上，若△A1OB1、△A2B1B2、△A3B2B3、…依次均為等腰直角三角形，直角頂點都在x軸上，則第n個等腰直角三角形AnBn-1Bn的頂點Bn的橫坐標為＿＿＿＿＿＿.

2.如圖4，一段拋物線：y=-x（x-2）（0≤x≤2）記為C1，它與x軸交于兩點O、A1；將C1繞點A1旋轉180°得到C2，交x軸于點A2；將C2繞點A2旋轉180°得到C3，交x軸于點A3……如此進行下去，直至得到C6，若點P（11，m）在第6段拋物線C6上，則m=＿＿＿＿＿＿.

3.如圖5，正△ABO的邊長為2，O為坐標原點，點A在x軸上，點B在第二象限，△ABO沿x軸作無滑動的翻滾，經一次翻滾后得到△A1B1O，則翻滾3次后點B對應的點的坐標是＿＿＿＿＿，翻滾2017次后AB的中點M經過的路徑長為＿＿＿＿＿.

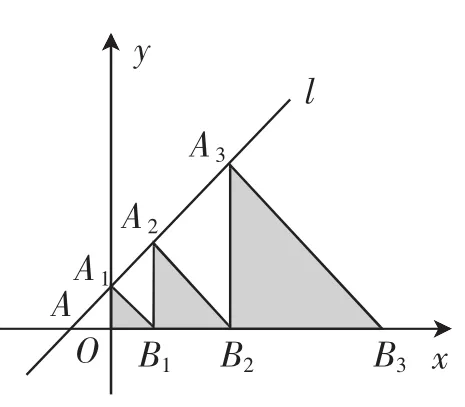
圖3

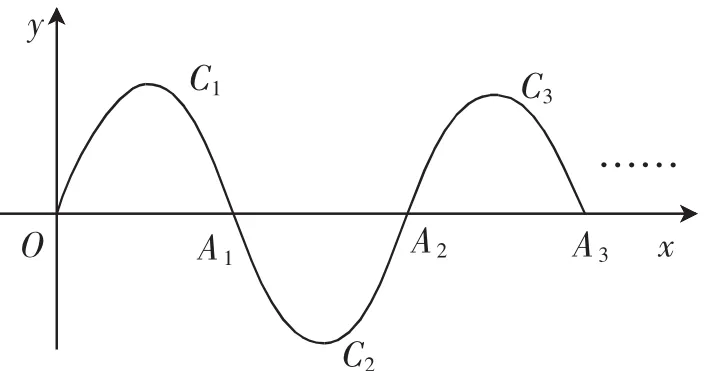
圖4

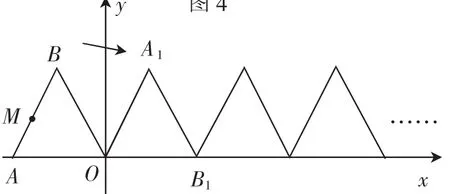
圖5

二、評課及修改教學設計

課后，筆者進行了深刻的教學反思，教學師傅也提出了建議和意見：在例題教學中，由于找規律題目可以有多種方法，學生疲于計算和接受，自主思考較少，教師講評較多，應當減少課堂容量，關注學生思考和互動；在練習環節，題目容量較大，計算量較大，學生無暇思考，課堂氛圍死氣沉沉，完全沒有達到預期目的，教師講評又太細，應增加師生互動環節，減少題目數量.

三、二次上課，迸發教學“火花”

聽取了教學師傅的建議和意見，結合筆者在教學過程中發現的問題，筆者對教學設計進行了一些修改：增加課前練習部分，啟發學生積極思考和互動；減少例題數量，同時積極啟發學生思考解題方法，主動獲取解題技巧.

【小試身手】

找規律，完成下列填空：

1.1，3，5，7，＿＿＿＿＿＿，11，13，…；

2.2，4，6，8，＿＿＿＿＿＿，12，14，…；

3.1，3，6，10，＿＿＿＿＿＿，21，28，…；

4.1，4，9，16，＿＿＿＿＿＿，36，49，…；

5.1，2，4，8，＿＿＿＿＿＿，32，64，…；

6.0，3，8，15，＿＿＿＿＿＿，35，＿＿＿＿＿＿，63，…；

7.2，6，12，20，＿＿＿＿＿＿，42，56，….

學生自主思考，然后分享解題技巧.

先呈現第1～5題，學生立刻找到答案，增強了學生的解題信心.第6～7題相對難度加大，學生解題速度減慢.完成后，學生回答.

生1：我發現第6題中的每個數都比第4題中的數少1，于是它的規律是n2-1.

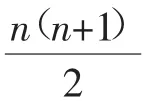
生3：我發現第7題中的數的規律很簡單，就是n（n+1）.

師：同學們，你們發現了嗎？這7道題中的數，我們都可以用字母表示出它們的規律，那就還可以用函數思想解決這種題目啊！

生4：哦，我明白了，把這些數設為y，把n當作自變量，當我找不到規律時就可以利用待定系數法解決了！

師：接下來我們試試吧.

【初探數式規律】

觀察下列等式：

……

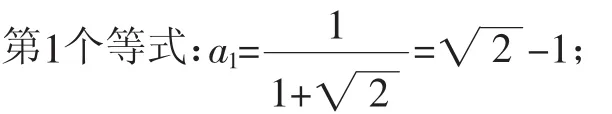
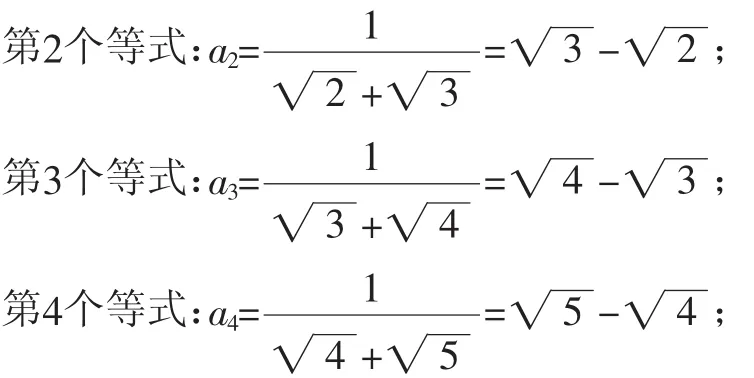
按上述規律，回答以下問題：

（1）用含n的代數式表示第n個等式：an=______；

（2）a1+a2+a3+…+an=______.

教師適當總結解題錦囊：

編序號—找“關系”—驗證.

【再探圖形規律】

例題教學：如圖1，自左至右，第1個圖由1個正六邊形、6個正方形和6個等邊三角形組成；第2個圖由2個正六邊形、11個正方形和10個等邊三角形組成；第3個圖由3個正六邊形、16個正方形和14個等邊三角形組成……按照此規律，第n個圖中正方形和等邊三角形的個數之和為______.

學生觀察、計算，教師板書：①6+6=12，②11+10=21，③16+14=30.

生1：我發現正方形的個數是6+5（n-1），等邊三角形的個數是6+4（n-1），所以個數之和是12+9（n-1）=9n+3.

生2：我發現后面一個數都比前一個數大9，所以規律是12+9（n-1）=9n+3.

生3：我用剛剛老師提到的函數思想試了一下，設個數和為y，函數解析式為y=kn+b，然后將（1，12）和（2，21）代入，解出解析式為y=9n+3，然后用（3，30）驗證了一下，發現解析式是正確的.

師：同學們思考出了很多解題方法，有的一眼就能看出，一下子看不出來時也可以考慮利用函數思想.不過一定要記住最后一步要驗證哦！

探囊取物：

如圖2，圖（1）是一個水平擺放的小正方體木塊，圖（2）、（3）是由這樣的小正方體木塊疊放而成的，按照這樣的規律繼續疊放下去，至第7個疊放的圖形中，小正方體木塊總數應是（ ）.

A.25 B.66 C.91 D.120

學生獨立思考，大部分學生學會先編序號，然后找關系，而不是一頭霧水，無從下手.教師讓學生回答解題方法時，很多學生積極回答問題.

生1：我發現各數依次是1、1+5、1+5+9，即1、1+1+4=1×2+4×1、1+1+4+1+2×4=1×3+4×（1+2）、…，那么第n個數就是n+4×［1+2+…+（n-1）］=n+2n（n-1）=2n2-n.

生2：我是用函數思想解答的，我發現這幾個數之間的變化符合二次函數，因此設函數解析式為y=an2+bn+c，然后分別將（1，1）、（2，6）、（3，15）代入，得到函數解析式是y=2n2-n.

師總結：所以我們以后碰到找規律題目時可以先編號，然后通過觀察數之間的內在規律或用函數思想解決.

這時，一學生舉手，說自己還有另外一種方法：我利用之前一道找規律題目（如圖6）找到了靈感.觀察，發現規律：1+3=22，1+3+5=32，1+3+5+7=42，…，則1+3+5+…+（2n-1）=n2.我觀察這幾個圖形的主視圖和左視圖發現它們正好符合這個規律，然后把主視圖和左視圖重復相加的部分n減去就可以了，因此這道題的規律就是2n2-n.

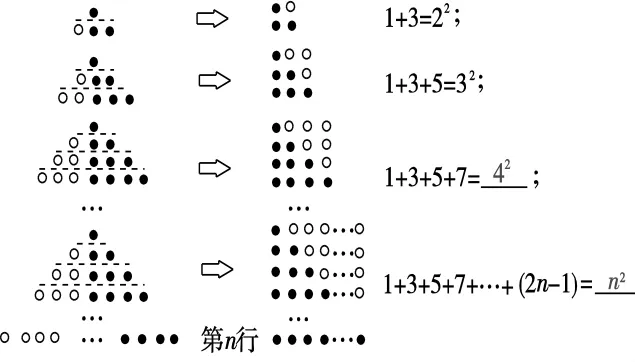
圖6

筆者、聽課的老師和全班學生無一不為之驚訝，都為其熱烈鼓掌，課堂氣氛達到高潮.

師：我們都學會如何解決找規律問題了，接下來，大家來試試第三種類型吧.

【三探坐標系中的規律】

如圖5，正△ABO的邊長為2，O為坐標原點，點A在x軸上，點B在第二象限，△ABO沿x軸作無滑動的翻滾，經一次翻滾后得到△A1B1O，則翻滾3次后點B對應的點的坐標是_____，翻滾2017次后AB的中點M經過的路徑長為_____.

四、二次評課

第二次的教學設計修改，得到備課組老師一致好評.這節課充分體現了教學相長的思想，教師在講授知識的同時與學生互動，學生也參與到教學活動中積極思考和熱烈討論，在這一過程中老師和學生都學到了新的技能和方法.

五、課后反思

在初中數學中，探索事物間的數量關系或變化規律是重要內容，探索和理解簡單的數量關系，探索和理解運算律，探索和理解具體問題中的變化規律等，這些都是初中生要掌握的知識，因此培養和發展學生探索規律的能力十分重要.在本節課中，筆者著重從以下幾個方面進行教學設計：

1.夯實學生的學習基礎

在學生初中三年的數學學習中，找規律題目出現的頻率較高，學生對其的熟悉度較高，但題型較多，學生難以找到解決問題的方法和技巧.因此在教學之初，設計幾個較簡單的找規律題目，學生在做題的同時，加深對找規律題的認識和理解，夯實學習基礎，易于接受知識點，為后續的教學活動做準備.

2.給學生提供合適的素材

在經歷第一次課的失利后，筆者深刻反思，課堂素材較多，較繁雜，計算量大，限制了學生的思考.經過修改，課堂素材精簡，在教學之初呈現較簡單的找規律題目，學生在做題的同時發現解題技巧；在學生發現解題技巧后，呈現一道數式規律題，學生在完成題目的同時，通過師生的交流和展示，學會運用多種技巧和方法解決問題；接下來依次呈現兩道圖形探索規律題，學生解題興趣濃厚，急于運用自己剛剛學到的方法解決，并在完成題目后獲得成就感.

3.積極啟發學生的思維

在小試身手環節，當學生面對較難題目時，適當指導學生觀察前面幾道題中數的規律，尋找數之間的內在規律，在學生展示后適當提到函數思想.共同完成兩道題的解決后，有學生發現并運用了函數思想解題，這時筆者提出函數思想，并適時提醒學生這種方法的好處及與其他方法的不同，拓展學生的解題思維.在學生想到新的解題策略時，為之鼓掌，表揚其發現問題、總結問題的好習慣，使學生在學習過程中積極動腦思考、及時總結和反思，促進學生更好地發展.

4.注重學生的自我展示

比較兩次課程設計，后者較重視學生的自我展示，學生在課堂上真正“有話可說”“有話能說”“有話想說”，成為課堂真正的主人，自主掌握自己的學習，并在學習過程中積極思考問題、參與課堂、學有所獲.

教學，顧名思義是教師的教和學生的學，是教師和學生之間的互動過程.離開學生的主動學習，課堂就會變成教師的“一言堂”，也就失去了教學的魅力，因此教師的教學應適合學生發展，基于學生基礎，啟發學生思考，調動學生學習的積極性，這樣才能在課堂上使學生真正參與到教學活動中，做到“有話可說”.