用好閱卷大數據,開展精準式講評
——從一次八上期末試卷講評說起
☉江蘇省海門市能仁中學 陸新鋒
學期末考試后,常常因為學期結束工作繁多,而忽略對試卷的講評,經過一個漫長的假期,返校之后忙于開學工作,以及“開學第一課”常常有新的教學內容要開展,所以又忽略了上學期期末試卷的講評工作,很多學生也忽略了對試卷測評之后的深度分析,使得一次重要的測試最后只是關注了一個分數,而缺少必要的講評與同類跟進,這是一種教學和評價的遺憾.基于以上認識,我們在成績出來之后,抽出時間及時組織了試卷講評,并將同類問題進行關聯或變式拓展,取得了較好的講評效果.本文梳理一節八上期末試卷講評的題例與變式,并給出相關教學思考,供研討.
一、八上期末試卷講評記錄
考題1:(考卷第18題,填空題最后一題)已知如圖1,平面直角坐標系xOy中,點B的坐標是(,0),點A在y軸的正半軸上,且∠BAO=30°,點C是線段OA上一點,以BC為邊向下作等邊三角形BCD.點C在y軸上從點A向點O滑動的過程中,點D運動的路徑的長度是_______.
講評手記:這道考題成功解出的學生只有5人,因為之前練習過同類習題,不少學生能找到一些轉化的方向,但是沒有獲得最后結果.究其障礙,在于以下幾處關鍵步驟,第一,沒有找準點C的起點、終點對應的旋轉后的起點與終點,如圖2中的點E、點F;第二,對旋轉前后全等三角形ABO、三角形EBF沒有想清對應關系;第三,對點D運動路徑即EF的長(對應著旋轉前的AO的長)理解不準.
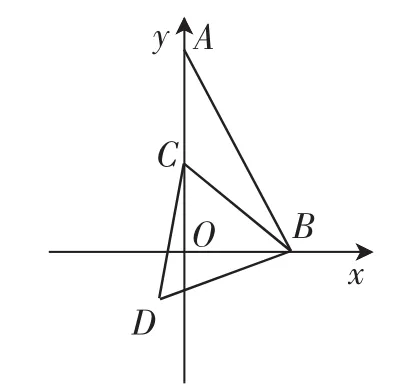
圖1
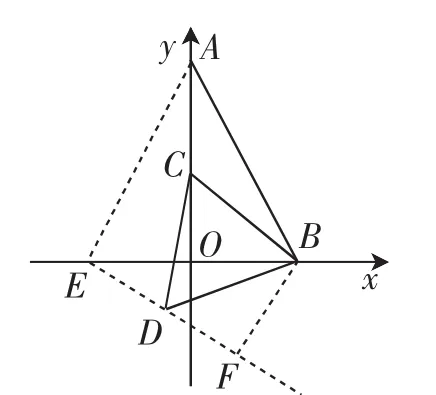
圖2
考題2:(考卷第27題,解答題倒數第二題)如圖3,平面直角坐標系中,點B的坐標為(2,0),以線段OB為邊在第一象限內作等邊三角形AOB,點C為線段AB延長線一點,連接OC,以線段OC為邊作如圖所示的等邊三角形ODC,直線DA交y軸于點E.
(1)求證△OAD △OBC.
(2)隨著點C位置的變化,點E的位置是否會發生變化?若沒有變化,求出點E的坐標;若有變化,請說明理由.

圖3
講評手記:將這道解答題提“前”講評,與考題1并列在一起,目的是讓學生識別同類問題,也是網上有些同行總結的所謂“手拉手模型”,△AOD △BOC,從而溝通對應角相等,通過“導角”,可得∠EAO=60°,從而有AD∥OB,于是DE⊥y軸,可確定OE就是等邊三角形OAB的高.
考題3:(考卷第28題,倒數第一題)如圖4,△ABC中,∠ACB=90°,AC=BC,過點C在△ABC外側作直線CP,點A關于直線CP的對稱點為E,連接BE交直線CP于點F,交直線AC于點M,連接CE、AF.
(1)若∠PCA=15°,求∠CBF的度數;
(2)請判斷△ABF的形狀,并說明理由;
(3)若45°<∠ACP<90°,補全圖5,用等式表示線段AC、EF、BF之間的數量關系,并說明理由.
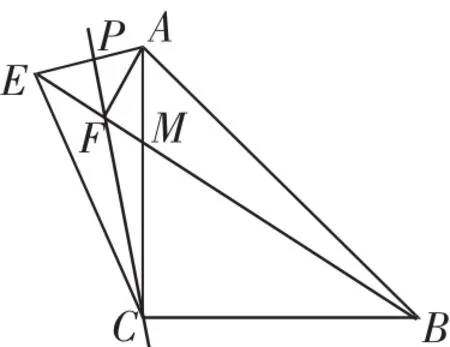
圖4
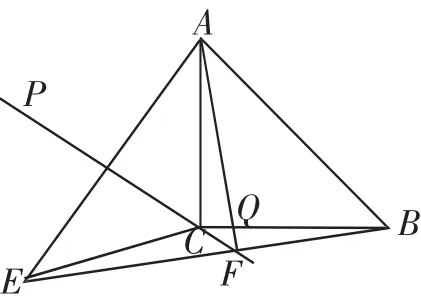
圖5
講評手記:第(1)問正確率高,多數學生根據對稱性先得出∠ACE=2∠PCA=30°,再把目光轉向等腰三角形BCE,可得底角∠CBF=30°;也有個別學生先把∠AFB為直角攻克成功,再逆過來分析∠CBF=30°.
(2)根據對稱性分析∠CEF=∠CAF=∠CBM,然后把目光投向△AFM和△BCM,利用三角形內角和性質可得∠AFM=∠BCM=90°,從而確定△ABF是直角三角形.
(3)在(2)的基礎上,在直角三角形ABF中,由勾股定理得AF2+BF2=AB2,再由EF=AF,AB2=2AC2,可得EF2+BF2=2AC2.
同類鏈接1:(2019年1月北京市朝陽區八上期末卷,第27題,有刪減)如圖6,已知C是線段AB的垂直平分線m上一動點,若點C在直線AB的上方,連接AC,以AC為邊作等邊三角形ACD,點D在直線AB的上方,連接DB,與直線m交于點E,連接BC、AE.當0°<∠CAB<30°時,用等式表示線段BE、CE、DE之間的數量關系,并證明.
思路預設:如圖6,在EB上截取EF,使EF=CE,連接CF.證出△CDF △CBE,則DF=BE,進一步代換出BE=CE+DE.
同類鏈接2:(2019年1月北京東城八上期末卷,第28題)如圖7,在平面直角坐標系xOy中,△ABO為等邊三角形,O為坐標原點,點A關于y軸的對稱點為D,連接AD、BD、OD,其中AD、BD分別交y軸于點E、P.點A在第二象限,此時AO與y軸的正半軸的夾角為α,60°<α<90°,用等式表示線段BP、PE、PO之間的數量關系.
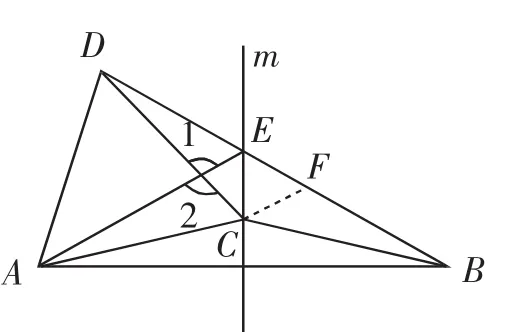
圖6

圖7
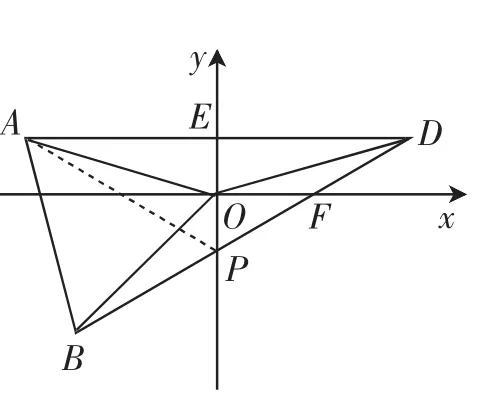
圖8
思路預設:如圖8,連接AP,先分析∠APE=∠APB=∠DPE=60°,由前面幾道題的解題經驗發現AP=BP+PO,再利用AP=PD=2PE可代換得2BP=BP+PO.
二、關于試卷講評課的三點思考
1.用好閱卷數據,有的放矢開展講評課
因為教育信息化的發展,現在很多地區期末考試都采取網上閱卷系統,提高閱卷工作效率的同時,也生成了閱卷大數據,這些閱卷大數據不止是均分、難度系數、區分度、信度等數據,對各個小題的小題分、小題閱卷數據的分析,有必要深度進行.在此基礎上,可以選取失分率高的小題進行重點突出的講評,技術助力增效,數據能提升試卷講評課的精準度.上面課例中的幾道考題也是我們基于閱卷大數據精選出來的一些典型考題,實施了重點講評、變式及鏈接拓展.
2.想清關聯試題,做好歸類講評與變式
基于閱卷大數據精準挑選待講評的考題之后,還需要對全卷中前后不同位置上具有關聯性質的試題一并呈現,并按由易及難的順序排列它們的呈現順序;再把不同類型的一些考試題組進行講評與變式,追求高效講評.比如,上面考題1、考題2是所謂“手拉手”全等模型問題,將其關聯在一起,有利于訓練學生發現問題深層結構的眼力,以便達到“講兩題、會一類、通一片”的高效教學效率.
3.重視同類跟進,收集同類題即時再練
考題3的講評之后,我們另選了一些同類題、變式題進行鏈接與拓展,幫助學生加深對這類問題思路突破的理解深度.事實上,這類問題在最近五年北京各區、各校的八年級和九年級試卷中有著“大量的存在”(感興趣的老師可搜集關注),這類問題與特殊三角形(等腰三角形)、軸對稱性質組合在一起,一是類值得關注的好問題,能有效訓練學生對等腰三角形“三線合一”、軸對稱性質、三角形內角和“導角”等知識的有效綜合.所以,通過較多同類問題的即時再練,可幫助學生感悟對這類問題求解的深刻理解.

